1. UVOD
Društvene mreže (engl. social networks) opisuju društvene strukture koje se sastoje od skupina ljudipovezanih odnosima kao što su prijateljstvo, srodstvo ili dijeljenje zajedničkih interesa (Milgram, 1967). Analiza društvene mreže ispituje društvenu strukturu koristeći metode iz područja analize kompleksnih mreža i teorije grafova. Osobe se predstavljaju kao „čvorovi“, a odnosi između osoba predstavljaju se kao „veze“ između čvorova (slika 1). Struktura tako definiranog grafa često je složena. Može biti više vrsta veza između čvorova. Multidisciplinarno istraživanje pokazalo je da društvene mreže mogu egzistirati na više razina, od obiteljskih odnosa do odnosa u državnim organizacijama i ustanovama. Analiza društvene mreže jedan je od važnih pristupa u suvremenim društvenim znanostima, među kojima su sociologija, antropologija, biologija, komunikacijske studije, ekonomija, zemljopis, informatika (Easley, Kleinberg, 2010). Pored kategorije društvenih mreža, teorija kompleksnih mreža obuhvaća još i tri druge važne kategorije kompleksnih mreža: biološke mreže, tehnološke mreže, informacijske mreže (Newman, 2010).
Izvor:Easley, Kleinberg(2010)
Jedna od potkategorija društvenih mreža jesu mreže koautorstva (engl. co-authorship networks) koja opisuje suradnju na znanstvenim publikacijama. Širi termin koji se koristi je mreže suradništva (engl. collaboration networks) koji podrazumijeva bilo kakav oblik suradnje u znanstvenom radu (suradnja na znanstvenim projektima, suradnja na zajedničkoj instituciji, suradnja u objavi publikacija i slično). U mreži koautorstva znanstvenici su prikazani kao čvorovi, a veza između dvaju znanstvenika (čvora) je uspostavljena ako su oni koautori na jednoj ili više znanstvenih (ili stručnih) publikacija. Takva mreža je neusmjerena, a može se promatrati i kao težinska mreža ako u obzir uzmemo broj znanstvenih publikacija na kojima su surađivala dva autora.
Ideja o izradi mreže koautorstva nije nova. Već se u sedamdesetim godinama prošlog stoljeća znanstvenici bave istraživanjima na tu temu. Mreža koautorstva prvi put prikazana je 1979. (Odda, 1979); bila je to mreža koautorstva matematičara Paula Erdösa koji je važan za razvoj područja teorije grafova(slika 2). U žargonu mreža koautorstva definiran je koncept „Erdös broj“(EN) koji predstavlja udaljenost između autora i Erdösa u mreži.Oni znanstvenici koji su objavili rad s Erdösom imaju EN = 1, oni koji su izdali rad s njima, ali ne i s Erdösom, imaju EN = 2 i tako redom.
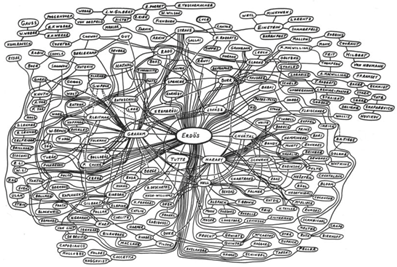
Izvor:Odda, (1979)
Nastavak trenda analize mreža koautorstava i mreža suradništva prisutan je i posljednjih petnaestak godina jer se područje analize kompleksnih mreža intenzivno razvija. U brojnim radovima analizirane su mreže koautorstva i mreže suradništva (Newman, 2004 a;Newman, 2004 b;Ramasco et al., 2004;Yoshikane, Kageura, 2004;Janssen et al., 2006;Lariviere et al., 2006;Chang et al., 2007;Bettencourt et al., 2009.;Pavlov, Ichise, 2007;Delgado-Garcia et al., 2014;Dias et al., 2014). U početnim istraživanjima (Newman, 2004 a;Newman, 2004 b;Ramasco et al., 2004;Yoshikane, Kageura, 2004) ustanovljena je sličnost između mreža koautorstva, ali i između svih društvenih mreža općenito. Uobičajeno je da su to mreže malog svijeta (Milgram, 1967;Watts, Strogatz,1998), odnosno da imaju male udaljenosti puta i relativno visok koeficijent grupiranja u odnosu na slučajnu mrežu iste veličine i mreže bez skale (Barabási, Albert, 1999) kod kojih distribucija stupnjeva prati takozvanu power-law distribuciju.
Rad Lariviereai suradnika (Lariviere et al., 2006) bavi se usporedbom mreža koautorstva za prirodne, društvene i humanističke znanosti znanstvenika u Kanadi. Chang i suradnici (Chang et al., 2007) analiziraju distribuciju stupnjeva i lokalna svojstva čvorova za mreže koautorstva. Pavlov i Ichise(Pavlov, Ichise, 2007) proučavaju mogućnost predviđanja eksperata za određeno znanstveno područje na temelju metode predviđanja veza u kompleksnim mrežama (engl. link prediction). Bettencourt i suradnici (Bettencourt et al., 2009) izučavaju razvoj i rast znanstvenih područja na temelju topologije mreža koautorstva. Neki noviji radovi (Delgado-Garcia et al., 2014;Dias et al., 2014) bave se analizom strukture mreža koautorstva znanstvenika na području Latinske Amerike. U spomenutim radovima analizira se struktura mreže na različitim razinama za različite primjene. Pored toga, pokazano je da sve analizirane mreže koautorstva imaju neka univerzalna svojstva.
Cilj istraživanja prikazanog u ovom radu bio je provjeriti imaju li mreže koautorstva nekih sastavnica Sveučilišta u Rijeci ista univerzalna svojstva (npr. svojstva mreže malog svijeta), te usporediti mreže međusobno i analizirati kako se ponašaju globalne, središnje i lokalne mjere mreža. Korištene su standardne metode analize kompleksnih mreža.
Prikazano istraživanje zamišljeno je kao preliminarno istraživanje mreža koautorstva Sveučilišta u Rijeci, pa su za prvu fazu analize odabrani samo Sveučilišni odjeli i Filozofski fakultet u Rijeci. Radovi Filozofskog fakulteta su (pored radova Sveučilišnih odjela) dodatno uključeni u analizu jer su neki Sveučilišni odjeli nekada bili odsjeci na Filozofskom fakultetu i jedan dio radova znanstvenika s odjela u bazi CROSBI vodi se kao radovi Filozofskog fakulteta. Takvim proširivanjem podataka ujedno je dobiven širi uvid u sliku stvarnog stanja znanstvene kolaboracije na Sveučilištu u Rijeci. Radovi Odjela za fiziku nisu uključeni u ovu preliminarnu analizu jer su se pojavili problemi prilikom prikupljanja podataka zbog nekonzistentnih podataka u bazi CROSBI. Iz tog razloga su konačni rezultati analize objavljeni za tri odjela (Odjel za informatiku, Odjel za matematiku i Odjel za biotehnologiju) te Filozofski fakultet u Rijeci.
U drugom poglavlju rada dan je pregled metodologije analize kompleksnih mreža. U trećem poglavlju opisana je analiza podataka. U četvrtom poglavlju izneseni su rezultati analize. Na kraju su iznesena zaključna razmatranja i ideje za nastavak rada na ovom istraživanju.
2. ANALIZA STRUKTURE KOMPLEKSNIH MREŽA
U ovom poglavlju opisane su metodeanalizestrukture kompleksnih mreža. Mreža se standardno prikazuje kao graf. Graf je uređen par G=(V,E) gdje je V skup vrhova, a E skup bridova. U terminologiji kompleksnih mreža vrhove nazivamo čvorovima (engl. nodes), a bridove vezama (engl. links).
Kompleksne mreže objedinjuju klasu mreža koje imaju neka zajednička istaknuta topološka svojstva kao što su, primjerice, mala prosječna duljina puta, visoki koeficijent grupiranja, hijerarhijske strukture, strukture sa zajednicama, pojavljivanje istaknutih čvorova sa stupnjem za red veličine većim od ostalih čvorova (engl. hubs). Kompleksne mreže mogu se analizirati na više razina: može se analizirati mreža u cijelosti (engl. global-scale level), središnja razina mreže (engl. meso-scale level) ili lokalna razina mreže (engl. local-scale level).Mreže koautorstva modeliraju se kao neusmjerena težinska mreža, pa su sve formule u ovom poglavlju iskazane za neusmjerene mreže. Neke formule ne uzimaju u obzir težine veza jer imaju smisla samo za netežinsku mrežu; u tom slučaju težinska mreža promatra se kao mreža bez težina.
2.1 Analiza mreže na globalnoj razini
Za analizu mreže na globalnoj razini koriste se mjere koje sagledavajumrežu u cijelosti. U daljnjem tekstu iznosimo formule za računanje osnovnih mjera mreže na globalnoj razini. Detaljni prikaz formula za analizu kompleksnih mreža dan je u (Newman, 2010.).
Stupanj čvora je lokalna mjera koja je definirana za svaki čvor, no potrebna je za razumijevanje nekih globalnih mjera, pa je navodimo odmah na početku. Za čvor v_i, stupanj čvora k_ije broj čvorova s kojima je čvor v_i povezan. Na razini cijele mreže zanima nas koji je prosječni stupanj mreže (engl. average degree). Ta vrijednost dobiva se kao omjer ukupnog broja stupnjeva mreže i broja čvorova:
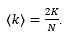 (1)
(1)
Na globalnoj razini promatra se distribucija stupnjeva kao funkcija koja opisuje kako se ponašaju stupnjevi čvorova u toj mreži. Distribucija stupnjeva mreže definira vjerojatnost da slučajno izabran čvor ima stupanj k (odnosno k susjeda). Ako je n(k)broj čvorova stupnja k, tada vrijedi:
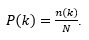 (2)
(2)
Kod težinskih mreža osim stupnja čvora ima smisla uzeti u obzir i snagu čvora (engl. node strength). Snaga čvora je zbroj svih težina na vezama koje ima taj čvor. Prosječna snaga mreže (engl. average strength) računa se kao:
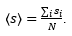 (3)
(3)
Nadalje, gustoća mreže je mjera gustoće veza i računa se kao omjer broja ostvarenih veza i broja mogućih veza:
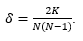 (4)
(4)
Za mrežu kažemo da je povezanaako između svaka dva čvora postoji put. Povezana komponenta grafa (engl. connected component) je podskup skupa čvorova za koji vrijedi: (1) za svaka dva čvora iz podskupa postoji put između tih dvaju čvorova i (2) podskup nije dio većeg podskupa s istim svojstvima (to je najveći takav podskup). Od interesa je promatrati broj povezanih komponenti u mreži koji označavamo sa ω. Za kompleksne mreže uobičajeno je da većina čvorova pripada jednoj velikoj komponenti koju zovemo najveća povezana komponenta (engl. ginat component), odnosno, tendencija mreže je povezivanje u jedinstvenu komponentu.Neke mjere kao što su, na primjer, mjere udaljenosti mogu se računati samo na povezanoj mreži, pa se u tom slučaju izračunavaju na najvećoj povezanoj komponenti.
Udaljenost između dvaju čvorova u mreži definiramo kao zbroj veza koji sačinjavaju put od početnog čvora do završnog čvora. Budući da u mreži općenito možemo imati i više različitih puteva između dvaju čvorova, njihove duljine ne moraju nužno biti iste. Mjera koja se često koristi je prosječna duljina puta (engl. average shortest path length). Prosječna duljina puta je prosječna vrijednost zbroja svih najkraćih puteva u mreži. Ako jed_ijnajkraći put između čvorova v_i i v_j, prosječna duljina puta u mreži dana je formulom:
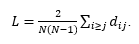 (5)
(5)
Što je prosječna duljina puta kraća, to je brže širenje informacija kroz mrežu.Dijametar mreže (engl. diameter)D je najveća udaljenost među njegovim čvorovima, odnosno najveća vrijednost između svih mogućih najkraćih puteva u mreži.
Koeficijent grupiranja (engl. clustering coefficient) je mjera koja nam govori koliko su čvorovi u mreži međusobno grupirani. Na lokalnoj razini razmatra se lokalni koeficijent grupiranja. Susjedstvo čvorav_i, N_i je skup svih čvorova koji su susjedni s čvorom v_i. Broj svih elemenata skupa N_i označava se sa K_i. Tada je koeficijent grupiranja čvora v_i određen sljedećom formulom:
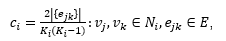 (6)
(6)
gdje je e_jk∈E oznaka za vezu koja povezuje čvorovev_j,v_k.
Na globalnoj razini gleda se prosječni koeficijent grupiranja:
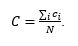 (7)
(7)
Njime mjerimo koliko je čvor povezan sa svojim susjednim čvorovima. Na razini cijele mreže određuje se koliko je cijeli graf blizu tome da tvori potpuni graf (engl. complete graph).
2.2 Analiza mreže na središnjoj razini
Zajednica je skupina zavisnih entiteta koji međusobno dolaze u kontakt, a na grafičkoj reprezentaciji se ističe kao skupina čvorova koji su relativno gusto povezani jedan s drugim, ali su labavo povezani s drugom skupinom čvorova – drugom zajednicom. Čvorovi u zajednici dijele slična svojstva ili imaju slične uloge u grafu. Proučavanje zajednica je složen proces koji zadire u područje raznih znanosti. Cilj takvog proučavanje je shvatiti kako, gdje i zašto se zajednice formiraju te na temelju interakcija pojedinih članova (mikroskopska razina) pokušati predvidjeti interakcije kompletne zajednice (makroskopska razina).
Definirani su brojni algoritmi za analizu zajednica u mreži. Pregled algoritama dan je u radu (Fortunato, 2010).
Podjela grafa na zajednice naziva se još i particija. Kod određivanja particije važno je znati koliko je particija dobra. Jedna od najčešće korištenih mjera kvalitete particije je modularnost (engl. modularity). Modularnost mreže koja je podijeljena na zajednice računa se pomoću formule:
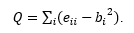 (8)
(8)
Član e_ij označava broj veza u mreži koje povezuju čvorove grupe i s čvorovima grupe j, a b_i se računa po formuli b_i=∑_j▒e_ij i označava broj veza kojima je jedan kraj u grupi i. Iz toga slijedi da je modularnost Q broj veza koje se nalaze unutar zajednica umanjen za očekivanu vrijednost jednakog broja veza koje su odabrane nasumično, bez obzira na pripadnost zajednici. Velik iznos modularnosti Q(veći od 0,7) pokazatelj je da mreža ima tendenciju grupiranja u zajednice.
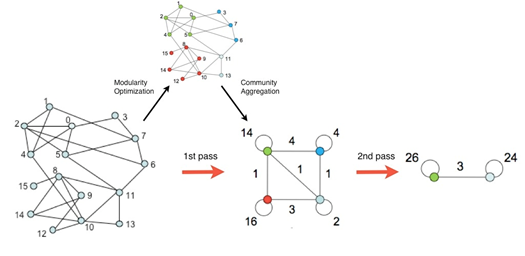
Nakon definiranja mjere modularnosti (Newman, 2006) razvijen je cijeli skup algoritama koji se temelje na optimizaciji modularnosti. To su algoritmi koji heurističkim pristupom pronalaze particije prema nekom definiranom pravilu i onda odaberu onu particiju koja ima najveću modularnost. Jedan od takvih algoritama je Louvainov algoritam (Blondel et al., 2008).
Louvainov algoritam izvodise u dvije faze. Prvo, otkriva „male“ zajednice optimiziranjem modularnosti. Zajednicu pronalazi tako da počinje od prvog odabranog čvora i za sve njegove susjede provjerava hoće li biti veća dobit na modularnosti ako se susjedni čvor pridruži zajednici ili ako se ne pridruži. Drugo, gomila čvorove iz iste zajednice i gradi novu mrežu čiji čvorovi su članovi te zajednice. Ti koraci se ponavljaju iterativno dok nije postignuta najveća moguća modularnost. Rezultat programa tako daje više particija. Particija pronađena nakon prvog koraka sastoji se od puno zajednica male veličine. Na sljedećim koracima sve veće i veće zajednice su pronađene. Taj proces dovodi do hijerarhijske dekompozicije mreže.
2.3 Analiza mreže na lokalnoj razini
Mjere centralnosti služe da bi se lakše primijetili ključni i važniji čvorovi u mreži. Neke od poznatijih mjera centralnosti su: centralnost stupnja čvora, centralnost blizine i centralnost međupoloženosti.
Stupanj čvora u analizi društvenih mreža označava koliko čvorova izravno može dohvatiti zadani čvor. Čvor koji ima najveći stupanj (može ih biti i više) zove sehub. Većinom veći stupanj čvora označava i veću važnost ili popularnost čvora u mreži. Za zadani čvor v_i, centralnost stupnja (engl. degree centrality) definirana je kao:
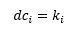 (9)
(9)
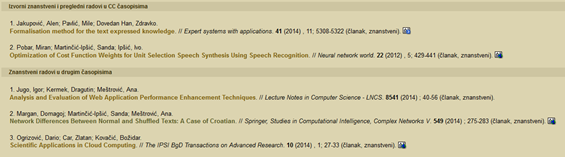
Centralnost blizine (engl. closeness centrality) određuje koliko brzo čvor može dosegnuti bilo koji drugi čvor u mreži, tj. koliko u prosjeku iznosi najkraći put do svih ostalih čvorova u mreži. Ova mjera je važna za slučajeve kada se zahtijeva velika brzina prijenosa informacije. Što je manja vrijednost, to je optimalna za prijenos informacije. Predstavlja važnost čvora u topološkom smislu, jer je čvor s najvišom centralnošću blizine najbliži ostalim čvorovima. Računa se kao recipročna vrijednost zbroja svih duljina najkraćih puteva od zadanog čvora do ostalih čvorova. Ponekad se dobivena vrijednost normalizira. Formula kojom se iskazuje vrijednost centralnosti blizine za pojedini čvor v_i je sljedeća:
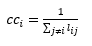 (10)
(10)
Centralnost međupoloženosti (engl. betweenness centrality) govori koliko je vjerojatno da se čvor nalazi na putu između neka dva čvora. Pokazuje koji čvorovi su više vjerojatni za prijenos komunikacije između dva druga čvora. Koristi se i kao pokazatelj gdje bi se mreža raspala, tj. koji bi čvorovi bili otkinuti ako nestane dio čvorova. Jednaka je broju najkraćih puteva koji prolaze kroz čvor podijeljenom sa svim najkraćim putevima u mreži. Normalizira se tako da je najveća vrijednost 1. Formula kojom se iskazuje vrijednost centralnosti međupoloženosti za pojedini čvor v_i je sljedeća:
 (11)
(11)
gdje je σ_hj (i) broj najkraćih putanja između čvorovav_h i v_j koje prolaze kroz čvor v_i, a σ_hj ukupni broj najkraćih putanja između čvorova v_hi v_j.
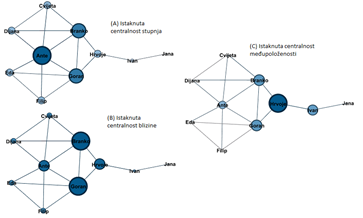
Za potrebe usporedbe različitih mreža, sve navedene mjere centralnosti moguće je iskazati kao normalizirane tako da ih se podijeli s ukupnim brojem čvorova (centralnost blizine) ili ukupnim mogućim brojem veza (centralnost međupoloženosti, centralnost blizine).Svaka od triju navedenih mjera centralnosti ima drugačiji smisao, pa samim time i drugačiju primjenu. Kako bi se ilustrirala različitost između opisanih triju mjera centralnosti, na slici 4 prikazana je ista mreža s istaknutim čvorovima ovisno o različitim mjerama centralnosti.
3. ANALIZA PODATAKA
Za potrebe istraživanja bilo je prvo potrebno prikupiti podatke, pripremiti ih tako da se prvo riješe problemi nekonzistencije, a potom transformiraju u odgovarajući format, odnosno mrežu u formatu liste bridova (engl. edgelist format). Nadalje su podaci analizirani metodama analize kompleksnih mreža. Podaci se analiziraju na globalnoj, središnjoj i lokalnoj razini. Za prikupljanje podataka, generiranje mreža i dio analize mreža napisali smo skripte u programskom jeziku Python; za prikupljanje podataka korišten je paket BeautifulSoup (Richardson, 2007), a za implementaciju i analizu mreža korišten je paket NetworkX (Schult et al., 2008). Za jedan dio analize mreža i vizualizaciju mreža korišten je softverski paket Gephi (Bastian et al., 2009).
3.1 Prikupljanje i priprema podataka
Za potrebe ove analize bilo je potrebno prikupiti podatke o autorima i naslovima znanstvenih radova Filozofskog fakulteta u Rijeci, te Odjela na riječkom Sveučilištu od kojih su neki prije spadali pod Filozofski fakultet.Ti su podacidostupni na mrežnim stranicama Hrvatske znanstvene bibliografije - CROSBI. Kako ne postoji gotovo sučelje za pristupanje podacima1, bilo je potrebno napisati programski kôd koji će prikupiti sve podatke i ispraviti pojedinačne pogreške kod nekih zapisa.
Prvo što moramo učini je proučiti strukturu podataka na stranicama. Budućida su svi odjeli isto strukturirani, kao primjer ćemo uzeti Odjel za informatiku. Slika 5 prikazuje kako je strukturiran zapis na samoj stranici. Zapis o radu je u obliku: redni broj. Podaci o autorima (Prezime, Ime) u prvom redu; nakon toga slijedi Naslov. u drugom redu te ostali podaci (Mjesto izdavanja : Nakladnik, Godina izdavanja.) odvojeno oznakom //.
Izvor: Obrada autora
Treba obratiti pozornost na pozicije interpunkcijskih znakova, poput točaka i zareza. Kod radova koji imaju više autora, imena autora odvojena su znakom točka sa zarez om „;“. Većina zapisa je tako strukturirana, no na žalost ne svi, jer bi tada bilo puno lakše pokupiti podatke sa stranice. Budući da postoje pogreške na stranici, poput krivo napisanih imena ili izmijenjenog redoslijeda podataka, treba u potpunosti pregledati sve zapise kako bi se podaci sa stranica prihvatili bez pogrešaka. Sljedeći korak je proučiti HTML zapis web-stranice da bi se uočilo kako su zapisani podaci, unutar kojih oznaka se nalaze podaci koji nas zanimaju.
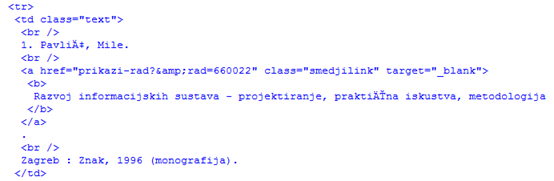
Na slici 6 prikazan je primjer jednog rada, jedne stavke u HTML zapisu. Ono što nas prvenstveno zanima, dakle autor i naslov rada, nalazi se u jednoj < br > oznaci. Unutar te oznake možemo vidjeti da se naslov nalazi pod oznakom < a > koja označuje link ili hipervezu. Svi naslovi su ujedno i link, s atributima class=“smedjilink“, target=“_blank“ i href=“prikazi-rad?&radX“, gdje X označuje kataloški broj rada na stranici. Atribut href nam ujedno daje i destinaciju gdje se nalazi znanstveni rad na webu.
Kako bi se ti podaci izvukli s web-stranice, korišten je programski jezik Python i paket za parsiranje HTML dokumenata, BeautifulSoup. BeautifulSoup radi stablo za parsiranje stranice koje se može iskoristiti za izvlačenje podataka iz HTML-a, tako da je vrlo koristan za postupak ekstrakcije podataka s weba (engl. web scraping, web harvesting, web data extraction). Za učitavanje mrežne stranice koristi se paket urllib2 koji Pythonu omogućuje dohvaćanje i čitanje mrežne stranice s interneta. Kao rezultat pohranjivanja podataka s web-stranice dobivamo objekt koji HTML zapis prikazuje kao ugniježđenu strukturu podataka.
Možemo vidjeti (slika 7) da se svi naslovi radova nalaze pod oznakom < a > koja unutar atributa href ima zapis „prikazi“.Pomoću BeautifulSoupa, koji nam omogućuje pretraživanje HTML zapisa i po atributima oznaka, našli smo sve linkove kojima se u atributu href nalazi riječ „prikazi“, te ih spremili u varijablu links (Naredeba: links = soup.findAll('a', href=re.compile("prikazi"))). Sljedeći korak je za svaki link a izvući samo tekst, bez dodatnih oznaka, te ga pohraniti u listu naslovi, a pri tome je potrebno izbrisati nepotrebne prazne redove. Nakon izbacivanja praznih redova dobijemo potpunu listu gdje je svaki naslov odvojena stavka.
Nakon toga je potrebno prikupiti podatke o autorima, istim redoslijedom kao i naslove. Naslove je bilo jednostavno izdvojiti, jer su već izdvojeni u samoj strukturi HTML-a. Kod izdvajanja imena autora ipak je bilo više problema. Oni se ne nalaze unutar određenih oznaka, te tako nisu definirani nikakvim atributima, ali možemo vidjeti (slika 7) da su smješteni između dviju < br/ > oznaka. Istina je da ih na samoj stranici ima jako puno, no samo naši autori se nalaze između dvije takve oznake. Osim toga, te oznake su braća u stablu, odnosno obje su djeca oznake < td >, koja ima atribut class=“text“. Imena autora su također braća tim oznakama, te ih tako možemo najlakše naći (Te oznake označuju line breaks). U ovom problemu najviše pomaže paket BeautifulSoup.

Traže se sve < br/ > oznake u tekstu i za svaku < br/ > oznaku se pokreće kod. U listu next spremamo sljedećeg brata od svake oznake < br/ > pomoću naredbe nextSibling. Tu su sada zapisana sva imena autora koja tražimo, al ne samo ona. Slijedi provjera o tome postoje li ta braća uopće i, ako postoje, provjerava se je li klasa tog objekta NavigableString. NavigableString je klasa objekta u BeautifulSoupu, koja nam govori da se radi o tekstu unutar oznaka. Ovime izbacujemo svu braću < br/ > oznaka koji ne sadrže tekst.
Sljedeći korak je da u listu next2 stavimo sljedećeg brata, dakle nextSibling od naše varijable next, kako bismo provjerili je li jednak oznaci < br/ >, budući da znamo da se naš tekst nalazi između tih dviju oznaka. Radimo još jednu posljednju provjeru kako bismo izbacili znakovne nizove između < br/ > oznaka koji su prazni. Zatim u listu autori_radovi spremamo sve znakovne nizoveiz liste next koji su prošli provjeru. Zatim moramo spojiti naslove i autore u rječnik, tako da su autori povezani s radovima koje su napisali. Rezultat tog postupka su radovi u rječniku zapisani tako da se naslov rada prikazuje kao ključ, a autori su vrijednosti povezane s ključem. Možemo vidjeti kako to izgleda na par primjera iz rječnika ({ label needed for fig[@id='graf8'] }slika 8).
Time je postupak obrade podataka završen, a konačan rezultat je rječnik s podacima o koautorstvu. Dakle sa stranice s listom svih znanstvenih radova Odjela za informatiku uspjeli smo prikupiti podatke o autoru i naslovu svakog rada. Ti podaci su obrađeni i na kraju zapisani u rječniku u obliku koji omogućuje analizu podataka. Taj isti postupak se jednostavno ponovi za preostale mrežne stranice koje istražujemo. Na kraju prvog dijela postupka podaci su pripremljeni za konstrukciju mreže.
{ label needed for fig[@id='graf8'] }

Izvor: Obrada autora
3.2 Generiranje mreže i analiza podataka
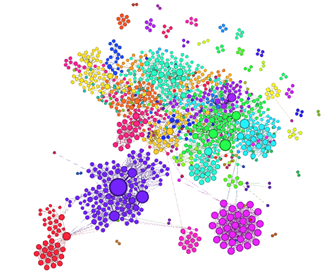
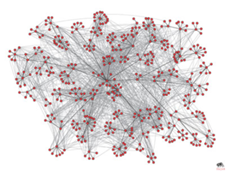
Iz prikupljenih podataka za svaku promatranu sastavnicu generirana je jedna izolirana mreža koautorstva s odgovarajućim nazivom: KOAINF (mreža koautorstva Odjela za informatiku), KOAMAT (mreža koautorstva Odjela za matematiku), KOABIO (mreža koautorstva Odjela za biotehnologiju), KOAFFRI (mreža koautorstva Filozofskog fakulteta u Rijeci). Pored toga generirana je i jedna jedinstvena mreža kao unija te četiri mreže s nazivom KOA. Vizualizacija cjelokupne mreže koautorstva, KOA prikazana je na slici 9.
Mreže su neusmjerene i težinske, bez petlji i višestrukih veza. Veze spajaju znanstvenike koji su zajedno objavili publikaciju, a težina veze pokazuje koliko su puta surađivali. Mreže su različitih veličina, a broj čvorova i veza prikazan za svaku mrežu prikazan je utablici 1.
| KOA inf | KOA mat | KOA bio | KOA ffri | KOA | |
|---|---|---|---|---|---|
| N | 90 | 44 | 182 | 909 | 1150 |
| K | 177 | 84 | 976 | 2735 | 3862 |
Izvor: obrada autora
Nakon konstrukcije provedena je analiza kompleksnih mreža na globalnoj, središnjoj i lokalnoj razini. Na globalnoj razini izračunate su numeričke vrijednosti osnovnih mjera: prosječni stupanj, najveći stupanj, prosječna snaga, prosječni koeficijent grupiranja, prosječni najkraći put, dijametar, gustoća, broj zajednica i broj komponenti. Na središnjoj razini identificirane su zajednice primjenom Luvainova algoritma i vizualizirane u alatu Gephi. Na lokalnoj razini analizirana je centralnost čvorova prema trima mjeramacentralnosti: centralnost stupnja, centralnost blizine, centralnost međupoloženosti.
4. REZULTATI
U ovom poglavlju prikazani su rezultati analize za svih pet mreža. Prikazane su globalne mjere mreže, vizualizacija zajednica i centralni čvorovi u mreži.
4.1 Numeričke vrijednosti globalnih mjera mreža
Numeričke vrijednosti globalnih mjera za svih 5 mreža prikazano je utablici 2. Rezultati pokazuju da postoje sličnosti između analiziranih mreža. Sve mreže imaju relativno male mjere udaljenosti, visoki koeficijent grupiranja, malu gustoću te tendenciju grupiranja u zajednice. Ako promatramo ukupnu mrežu, možemo uočiti sljedeće: dijametar za najveću promatranu mrežu KOL iznosi 16. Znači da informacija mora prijeći najviše 16 skokova da bi došla od jednog do drugog čvora. Prosječna duljina puta je 5.583. Ako promatramo mrežu po komponentama, možemo izračunati da ih ima 54. Jedna je divovska komponenta, najveća komponentu u grafu koja obuhvaća važniji dio grafa. Nju čini 706 čvorova, što je samo 61% cijele mreže.
Izvor: obrada autora
Nadalje, male mjere udaljenosti i visoki koeficijent grupiranja ukazuju na to da su sve mreže koautorstva mreže malog svijeta. Konačnu potvrdu te hipoteze možemo dokazati ako usporedimo postojeću mrežu s Erdős–Rényi mrežama iste veličine kod kojih se L i C mogu jednostavno dobiti prema sljedećim formulama: LER = lnN/ln<k> i CER= <k>/N, a pokaže se da je C>CER i L~LER. Za mrežu KOA koeficijent grupiranja pripadajuće slučajne mreže iznosi 0,006, što znači da je koeficijent grupiranja mreže koautorstva 100 puta veći od slučajne mreže. Prosječna duljina puta slučajnog grafa iznosi 3.71, što je vrlo blizu prosječnoj duljini puta mreže koautorstva. Ove dvije činjenice potvrđuju hipotezu da se radi o mreži malog svijeta. Taj rezultat u skladu je s dosadašnjim istraživanjima za druge mreže koautorstva.
Potrebno je naglasiti i to da postoje određene razlike između pojedinačne četiri mreže. Dvije mreže su manje, (KOAINF,KOAMAT) te imaju manji prosječni stupanj, manji najveći stupanj (kmax), i manju snagu. Te vrijednosti upućuju na smanjenu suradnju tih sastavnica u odnosu na druge dvije sastavnice (KOABIO,KOAFFRI). Ukupni najveći stupanj među svim sastavnicama iznosi 110 i upućuje na to da je najjača znanstvena suradnja ostvarena na Odjelu za biotehnologiju.
4.2 Analiza mreža na središnjoj razini: identifikacija i vizualizacija zajednica
Na središnjoj razini analizirana je modularnost svih mreža. Rezultati modularnosti su sljedeći: Q(KOAINF) = 0,658; Q(KOAMAT) = 0,796;Q(KOABIO) = 0,55;Q(KOAFFRI) = 0,891; Q(KOA) = 0,892. Budući svih pet mreža ima relativno visoku modularnost interesantno je analizirati zajednice u mrežama. Na slici 10 vizualizirano je grupiranje u zajednice za 4 izolirane mreže.
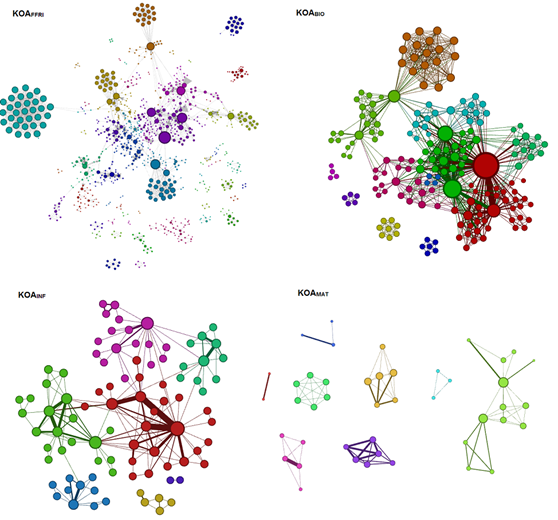
Izvor: Obrada autora
Na prikazanoj slici 10 debljina veze i veličina čvora proporcionalne su broju kolaboracija. Ovdje je važno napomenuti da suradi bolje vizualizacije veličine čvorova prikazane relativno. Naime, u jedinstvenoj mreži, najveći čvor KOAINF trebao bi biti znatno manji od najvećeg čvora mreže KOABIO, ali u takvoj vizualizaciji većina čvorova bila bi premala za vizualizaciju, pa je svaka mreža generirana zasebno i čvorovi u manjim mrežama veći su u odnosu na realno stanje.
Pokušali smo ispitati razlikuju li se mreže prema svojstvu grupiranja u zajednice. Moguće je vidjeti da se čvorovi na različite načine grupiraju u zajednice u tim mrežama. Na primjer, u mreži KOAINF postoje veze između zajednica, a samo su tri izdvojene komponente u grafu. S druge strane, u mreži KOAMAT 8 zajednica poklapa se s 8 odvojenih komponenti u mreži. To znači da između znanstvenika te sastavnice uglavnom ne postoji suradnja na publikacijama izvan definiranih komponenti, dok na prvoj sastavnici znanstvenici surađuju u različitim grupama. Druge dvije mreže koje su veće također nemaju izolirane zajednice, tu se može primijetiti postojanja većih klika2, bilo kao izoliranih zajednica (KOAFFRI) ili kao dijela zajednice (KOABIO).
4.3 Analiza mreža na lokalnoj razini: centralni akteri u mrežama koautorstva
U ovom dijelu posebno ćemo se fokusirati na različite mjere centralnosti. Analizirat ćemo centralnost stupnja, centralnost blizine i centralnost međupoloženosti samo za mrežu KOA jer nas zanima centralnost čvorova u cjelokupnim podacima.
Izvor: obrada autora
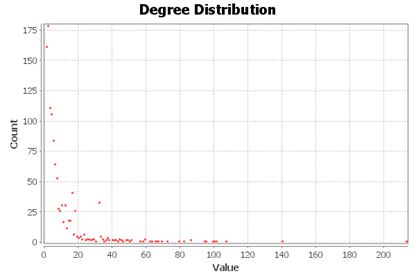
Centralnost stupnja čvora rangira znanstvenike prema broju drugih znanstvenika s kojima su objavljivali zajedničke publikacije. Utablici 3 rangirano je prvih 10 čvorova prema vrijednostima centralnosti stupnja. Prvih 10 znanstvenika ima prilično velik broj ostvarenih koautorstava, međutim prvi ima za red veličine veću centralnost od desetog. Takav trend se nastavlja i s drugim čvorovima (znanstvenicima), što se može vidjeti naslici 11. Očito je da stupanj vrlo brzo počne padati, te da veliki broj znanstvenika zapravo ima puno manji broj koautorstava s drugim znanstvenicima. Iz tih podataka može se naslutiti da distribucija mreže KOA prati power-law distribuciju, što ukazuje na to da se radi o mreži bez skale (Barabási, Albert, 1999).
Centralnost blizine prikazuje važne čvorove koji su vrlo blizu, i mogu brzo komunicirati s ostalim čvorovima u mreži. Utablici 3 prikazano je prvih 10znanstvenika koji imaju najveću vrijednosti centralnosti blizine. Međutim, vrijednosti za centralnost blizine ne variraju mnogo i sve su iz segmenta [1,12]. Iz analize proizlazi da centralnost blizine i nije toliko važna i reprezentativna mjera za mreže koautorstva.
Centralnost međupoloženosti nam prikazuje važne autore koji su postavljeni na velikom broju puteva između ostalih čvorova u mreži. Ako maknemo ove čvorove, moguće je da će se graf podijeliti na nepovezane grafove. Utablici 3 prikazano je prvih 10 autora koji imaju najveću vrijednosti centralnosti međupoloženosti, nocentralnost međupoloženosti također nema neku značajnu interpretaciju kod analize mreža koautorstva.
Različite mjere centralnosti imaju različite interpretacije. U radu je, međutim, pokazano kako za analizu mreže koautorstva ima najviše smisla analizirati centralnost stupnja koja nam direktno pokazuje koji autori imaju najveći brojsuradnji.
5. ZAKLJUČAK
U ovom radu opisana jepreliminarna analizamreža koautorstva Odjela za informatiku, Odjela za matematiku, Odjela za biotehnologiju te Filozofskog fakulteta Sveučilišta u Rijeci.
U prvom dijelu analize bilo je potrebno prikupiti podatke i pripremiti ih za konstrukciju mreže. Nakon obrade i usklađivanja podataka slijedio je dio izrade, analize i vizualizacije četirijuodvojenih mreža koautorstva znanstvenika svakog odjela (KOAINF,KOAMAT,KOABIO,KOAFFRI) i jedinstvene mreže(KOA) koja predstavlja uniju tih četiriju mreža.
Proučavanjem numeričkih vrijednosti mreže ustanovili smo da sve mreže imaju sličnu strukturu. Zbog visokog koeficijenta grupiranja i relativno male prosječne duljine puta možemo zaključiti da se radi o mrežama malog svijeta. Dobiveni rezultati u skladu su s rezultatima prikazanim u drugim radovima koji se bave analizom mreža koautorstva i potvrđuju univerzalnu strukturu mreža koautorstva.
Nadalje, sve analizirane mreže koautorstva imaju tendenciju grupiranja u zajednice (visoke vrijednosti modularnosti), pa smo identificirali zajednice u svim mrežama primjenom Luvainova algoritma. Analiza i vizualizacija zajednicaotkrivaju različitosti u strukturi zajednica na središnjoj razini mreže.
Daljnjom analizom mreže na lokalnoj razini prikazano jekoliko kolaboracija imajuistaknutiznanstvenici.
Prikazana analiza ukazuje na to daanalizakompleksnih mreža ima potencijala za ozbiljne analize bibliografskih podataka i suradnji između znanstvenika. Provedena analiza daje naznake da bi se slične analize mogle koristiti u postupcimaevaluacije suradnje u akademskoj zajednici.Također, daljnjim proučavanjem mreža, te proširivanjem objekta promatranja na cijelo Sveučilište u Rijeci, mogu se dobiti još precizniji podaci o znanstvenoj suradnji na Sveučilištu u Rijeci.