Semantically Enabling Map Projections Knowledge

1. Introduction

Map projections are a critical component of any continental or global distribution of geospatial, topical thematic, or temporal data shown on a map. Examples include population distribution, land cover/use, elevation, transportation, and image data of any form. Each data type and geographical area, continent, region, or globe, require appropriate selection of a map projection to display the data accurately and support the map design objectives. Traditional perspectives on map projection trade equality of area and conformality (equality of angles), but a plethora of objectives (distance, direction, specific lines of equality, global look, and others) can be optimized using correct projection transformation equations.

This paper provides a basic presentation of map projection characteristics, the potential selection of equations, types and examples, which leads to a classification system. The characteristics preserved in a map projection transformation from spherical or ellipsoidal equations to plane coordinates and classification are a knowledge base that can be used for human and machine selection of an appropriate map projection. The organization of this classification system and its elements form an ontology or metadata that guide users to map projections knowledge. The implementation of this knowledge base includes individuals of the classes and the properties semantically linked thus forming a knowledge graph to achieve a human and machine usability. This research examines that representation using basic principles from the World Wide Web Consortium for semantic data representation as linked data.

2. Basics

Map projection transformations convert geographic coordinates, latitude and longitude, from the globe to plane coordinates, x and y to create a map. The entire process is modeled by two generic equations:

x = f₁ (φ, λ), (1)

y = f₂ (φ, λ) (2)

where:

x and y are the projected plane coordinates,

φ and λ are latitude and longitude, respectively,

f1 and f2 are the functional forms for the transformation.

The transformation cannot preserve all characteristics from the globe to the map and some distortion occurs in any projection. Selecting the functional form of f1 and f2 determines the characteristics of the transformation that will reflect the final form of the map. Specific characteristics can be preserved with the correct equations for the transformation. Commonly the functional form preserves area, angles, distance, direction, or other spatial attributes or specific characteristics. Since an infinite number of forms of Eq 1 and 2 are possible, and several hundred or more have been developed, it proves useful to classify specific transformations to organize map projections knowledge.

Map projections classifications have been based on form of the transformation, appearance of the final map, usually based on the shape of the graticule of latitude and longitude, area mapped, and others. Additional criteria for classification are based on mathematical functions, ability to preserve characteristics, and others. Each of these classifications provides useful groupings and knowledge of the characteristics of map projection transformations. Several classifications are presented below and form the basis for a map projections knowledge base.

3. Classification

Map projections are usually classified according to the characteristics preserved by the transformation from the globe to the plane. Classifications are based on the shape of the normal graticule, parametric classification, geometry, or special properties (Canters 2012). These classifications provide a basis for semantic organization of map projections knowledge. The graticule classification is based on the shape of the latitude and longitude lines which define specific patterns resulting from the type of equation used for the transformation. Tobler’s classification by mathematical functions is the most comprehensive and logical organization, given that projections are based in mathematics (Tobler 1962); however, it is not widely used because of the abstract categories it produces. Maling’s classification into named geometric categories can be mapped to Tobler’s classes, but does not include all of the mathematical forms (Maling 1973,Canters 2012). Each classification scheme forms a single semantic representation however, the various classifications can be represented if we use the basic semantic concepts of map projections which underlie all classifications, and one set of classes and subclasses as the user interface to the knowledge. It still requires a single classification to define the classes, subclasses, instances, and properties that will be used in the semantic representation. Thus, this paper adopts the geometry class system since it appears to be the most intuitive to map readers and most commonly used. The classes of azimuthal, cylindrical, conical, pseudocylindrical, and space (Snyder 1987) and other projections (including Maling’s pseudoconical, pseudoazimuthal, and polyconic classes) form the class system to be used in this knowledge base. A complete class and subclass hierarchy is shown in the appendix.

4. Knowledge Representation and Semantics

Knowledge is represented as statements of facts with relations to other facts. For example, Croatia is a country, is a fact which could be a part of a geographic knowledge base. Semantics comprise meaning as expressed in the branch of linguistics and logic. Geospatial semantics express meaning to geographic objects, concepts, processes, and geographic terms and actions indicated by those terms, among others. Geospatial semantics allow building a knowledge representation. The following section describes basic semantic concepts and relates them to geospatial knowledge of map projections. Succeeding sections describe an implementation of a map projections knowledge base using semantic technology.

Semantic Web

The Semantic Web provides a platform to implement a semantic knowledge base. With its graph data structure based on triples, the Semantic Web allows access to knowledge that can be processed both by humans and machines (Feigenbaum et al. 2009). This research adopts the basic principles of the Semantic Web which are briefly described below and referenced for complete details (W3C 2020).

RDF and triple model

The Semantic Web uses the Resource Description Framework (RDF) triple model for storage and access of data (W3C RDF 2020). Each triple is a single data element and is structured as subject, predicate (property), and object. Subjects for the triple for a map projections statement are classes or individuals. Predicates are connections between the subject and the object. The object is also a class, individual, or another object including literals. The form of the statement is subject, predicate, object, much like verbal language. For example, projection preserves property, where projection is subject, preserves is predicate, and property is object.

Subjects

Subjects are the classes in map projections where classes are collections of similar projections based on a particular characteristic. Subjects may also be individuals. For example, single projections such as the Mollweide are subjects. Also, a map projection creator, Karl Brandan Mollweide, is another example of an individual that is a subject. All azimuthal projections form a class different from cylindricals and conicals (Snyder 1987). These mathematical characteristics impart a final look to the projected map, hence the names. These are classes in semantics and subclasses are particular projections, the Lambert Azimuthal Equal Area, for example.

Predicates (Properties)

The objective of any map projection is to preserve some characteristics from the globe representation of the Earth. Thus, logical predicates for map projection classes and instances are, ‘preserves a particular characteristic.’ For example, commonly one preserves area, angles, distance, direction, global look, rhumb lines, great circles as straight lines, overall shape of the Earth as circle, oval, rectangle, square, diamond, and any of various shapes desired by the user. The semantic statement then takes the form: subject preserves object. Objects are then area, angle, distance, and others. An example is shown below in English later to be expressed in Terse RDF Triple Language (Turtle), a triple format of the Semantic Web.

Mollweide preserves areas.

Equidistant cylindrical preserves distances.

Lambert Conformal Conic preserves angles.

Conformal projections preserve angles.

Note that in the first three cases the subject is a particular projection, although its final form will depend on the parameters such as the center of the projection, and others. In the last case the subject is a class of projections conformals. Since all conformal projections preserve angles and the Lambert Conformal Conic is a conformal projection (subclass of conformals), it also must preserve angles.

Objects

As discussed above, objects are either projections (individuals in semantic terms), classes, things such as areas, angles, literals, and many others. An example of projection as an object is John P. Snyder created the Space Oblique Projection, SnyderJohnP created spaceOblique. Space Oblique Projection is the object. This class of object semantics includes those things that are the logical semantical conclusion to the triple statement. For many semantic statements about map projections, the object is a particular projection, a property that is preserved, for example: Mercator preserves angles; and Mollweide preserves area.

5. Example implementation in Protégé

The Protégé Ontology editing software (Musen 2015,Protégé 2020) was used to develop the ontology of projection classes, subclasses, individuals, and properties and create a Web Ontology Language (OWL) file. Protégé and the OWL Protégé output support descriptive logic axioms and thus the knowledge graph can be used with this logic for reasoning and inference. The class hierarchy is shown inTable 1. The graphic inFigure 1 shows the classes, subclasses and lists the individuals in a WebVOWL presentation (WebVOWL 2020).

Table 1. Map Projections ontology class hierarchy. / Tablica 1. Hijerarhija klasa ontologije kartografskih projekcija

Figure 1. Class hierarchy graph connection of classes, subclasses, and object properties in the map projections knowledge graph shown in WebVOWL, a visualization package for RDF graphs and Web Ontology Language (OWL) datasets. Note the graphic shows classes and subclasses with individuals for the selected class, in this case cylindricals, shown in a list on the right panel of the figure. The numbers in the circles indicate the number of individuals in the class. / Slika 1. Grafički prikaz hijerarhije klasa: povezanost klasa, podklasa i svojstava objekata u grafičkom prikazu znanja o kartografskim projekcijama prikazan WebVOWL-u, vizualizacijskom paketu za grafove RDF-a i skupove podataka Web Ontology Language (OWL). Treba obratiti pažnju na to da grafički prikaz pokazuje klase i podklase s jedinkama za izabranu klasu, u ovom slučaju cilindričnim projekcijama, što se prikazuje kao popis na desnoj strani. Brojevi u kružnicama označavaju broj jedinki u klasi.

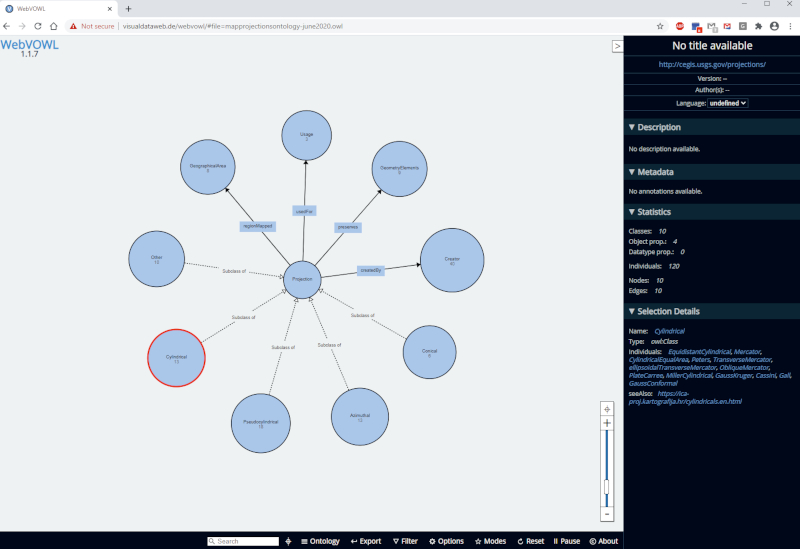
Object properties are shown inTable 2. These properties are used to establish the relationships between the map projection and the geometric element and geographical area individuals shown inTable 3 and4.

Table 2. Object properties in the Map Projections Ontology / Tablica 2. Svojstva objekata u ontologiji kartografskih projekcija

Table 3. Geometric Elements / Tablica 3: Geometrijski

Table 4. Geographical Area / Tablica 4: Geografsko područje

The properties for assigning characteristics though the triple model are structured as Annotation Properties. These properties include specifications about the projections and their properties, such as definitions, formula, graphics, and additional information from Web sources with a seeAlso property. The list of basic properties in the current map projections ontology is shown inTable 5.

Table 5. Annotation properties used in the map projections ontology./ Tablica 5: Anotacijska svojstva upotrebljena u ontologiji kartografskih projekcija.

The remaining individuals for projection types and creators are shown in the lists in the appendix

6. Use Cases and Results

Specific use cases for map projections demonstrate the capability to answer specific queries related to the knowledge base. Generally, map projections are selected and used to preserve particular characteristics from the globe. The use cases below are structured as SPARQL RDF Protocol and Query Language (SPARQL) queries. The use case is first expressed in plain English, then followed by the SPARQL query syntax with the result then expressed in plain English. For the final map projections knowledge graph, a semantic endpoint supporting SPARQL queries is being deployed and will be made available to the public through the Map Projections Commission website (https://ica-proj.kartografija.hr/).

Use cases

The use cases below take the form: select the best map projection for specified conditions. In each case the result is single or multiple map projections. In the case of multiple projections in the result, all are presented to the user for selection. By default, the first in the list would be used by a machine access but a human user can select another from the list. Additionally, queries for determining the characteristics preserved by a particular map projection are shown.

1: Select the map projection that is best for a map of an areal distribution in the mid latitudes. For example, mapping the areas of states in the United States.

The result finds the Albers Equal Area Conic projection.

2: Select the best projection for navigation on the entire globe.

The result finds the Mercator projection.

3: Select the best projection for large scale topographic mapping.

The result finds the Transverse Mercator projection.

4: Select all projections in the knowledge base that preserve true direction (azimuths).

The result finds the following:

Orthographic

Stereographic

Polyconic

5: Select all projections that are in the Azimuthal class

The results are:

Stereographic

Orthographic

WagnerVII

Airy

Gilbert

Azimuthal Equidistant

Gnomonic

Aitoff

General Perspective

Hammer

Lambert Azimuthal Equal Area

6: Find equal area projections appropriate for latitudes around the Equator

The results are:

Cylindrical Equal Area

EqualEarth

Eckert IV

Eckert VI

Mollweide

Sinusoidal

7: Learning map projections theory and use:

To address this use case the ontology must access Web resources to retrieve characteristics by connection to existing Universal Resource Locations (URLs) that provide accurate formulas, text, and graphics for the selected projection or group of projections. As an example:

Describe characteristics of Azimuthal projections.

This query returns the link to a web resource which can be automatically engaged:

"https://ica-proj.kartografija.hr/azimuthals-and-related-278.en.html"

The knowledge base can only answer queries based on the information stored as triples and relations among them. At present it is a small limited prototype that represents primitives of map projections knowledge that can be built by the community and hosted by the Map Projections Commission of the International Cartographic Association (ICA). For example, each of the projections in the knowledge graph now have properties limited to the few best known: area, angle, direction, distance, region mapped, usage, mathematical formulation, graphic representation, and creator. Since the basic map projection equations for transformation from the sphere to the plane can be set to model infinite sets of geometric and topologic representations, the knowledge base needs expansion. Distortion characteristics by class and individual projections, shape preservation indices, and many others can be added to the knowledge base and enrich knowledge of map projections for the community. Other classifications can be incorporated and cross-mapped to the existing classes. For example, Tobler’s mathematical classes can be mapped to the existing classes with one-to-many and many-to-one relationships.

The current ontology and RDF triplestore can only be accessed through SPARQL queries or through ontology software such as Protégé. To be broadly useful a natural language interface and SPARQL query builder must be added. Including competency questions that can be answered through inference and OWL logic will also enhance the capability and utility of the knowledge base. Such interfaces are being developed for use on the Semantic Web to provide easier and broader access to ontologies and knowledge bases.

7. Conclusions

An initial ontology for map projections knowledge has been developed. The ontology can be used for map projection selection, pedagogy, determining appropriate projections, and direct query. The ontology is built from RDF triples developed in the Protégé ontology editing software. The final ontology is an OWL file which can be established as a SPARQL endpoint that can be accessed by anyone. The target location for a final version of this ontology is as an accessible endpoint on the ICA Commission on Map Projections website. A set of examples use cases illustrates the potential of such an ontology and provides working examples of how the ontology can be queried for information.

Acknowledgements

The author appreciates the detailed comments of the anonymous reviewers who provided review and suggestions that substantially improved the paper.

Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

1. Uvod

Kartografske su projekcije kritična komponenta bilo koje kontinentalne ili globalne raspodjele geoprostornih, tematskih ili vremenskih podataka prikazanih na karti. Primjeri takvih podataka su raspodjela stanovništva, pokrivenost/upotreba zemljišta, visina, prijevoz te slikovni podaci u bilo kojem obliku. Svaki tip podataka i geografsko područje, kontinent, regija ili svijet zahtijeva odgovarajući odabir kartografske projekcije koja će točno prikazati podatke i poslužiti svojoj svrsi. Tradicionalno se na odabir kartografske projekcije gleda kao na kompromis između očuvanja površina i konformnosti (očuvanja kutova), no upotrebom jednadžbi za transformaciju kartografskih projekcija moguće je optimizirati velik broj ciljeva (udaljenost, smjer, specifične linije jednakosti, opći izgled, itd.).

Ovaj rad opisuje osnovna svojstva kartografskih projekcija, moguć odabir jednadržbi, tipove i primjere, što dovodi do klasifikacijskog sustava. Svojstva očuvana transformacijom kartografskih projekcija iz sfernih ili elipsoidalnih jednadžbi u koordinate u ravnini i klasifikacija predstavljaju bazu znanja koju ljudi i strojevi mogu primijeniti za odabir odgovarajuće kartografske projekcije. Organizacija tog klasifikacijskog sustava i njegovih elemenata predstavlja ontologiju ili metapodatke koji vode korisnike prema znanju o kartografskim projekcijama. Primjena te baze znanja uključuje jedinke klasa i njihova svojstva povezane semantički, što daje grafikon znanja koji mogu upotrijebiti ljudi i strojevi. Istraživanje se bavi tom reprezentacijom upotrebom osnovnih načela World Wide Web Consortiuma za semantičko prikazivanje podataka kao povezanih podataka.

2. Osnove

Transformacije kartografskih projekcija pretvaraju geografske koordinate (geografsku širinu i geografsku dužinu) iz koordinata na globusu u koordinate u ravnini (x i y) kako bi se moglo izraditi kartu. Čitav proces opisuju dvije općenite jednadžbe:

x = f₁ (φ, λ), (1)

y = f₂ (φ, λ) (2)

gdje su:

x i y koordinate u ravnini,

φ i λ su geografska širina i geografska dužina,

f1 i f2 su funkcije za transformaciju.

Takva transformacija ne može očuvati sva svojstva s globusa te se u svakoj projekciji javljaju neke deformacije. Odabir funkcija f1 i f2 određuje svojstva transformacije koja će također odrediti i konačan oblik karte. Određena svojstva mogu se očuvati odgovarajućim jednadžbama transformacije. Funkcije će najčešće očuvati površinu, kuteve, udaljenost ili druga prostorna svojstva ili određena svojstva. Budući da je moguć beskonačan broj jednadžbi (1) i (2), a razvijeno ih je nekoliko stotina ili više, pokazalo se korisnim klasificirati određene transformacije za organizaciju znanja o kartografskim projekcijama.

Dosadašnje klasifikacije kartografskih projekcija temeljile su se na obliku transformacije, izgledu konačne karte, obično na temelju oblika mreže meridijana, područja kartiranja i dr. Dodatni kriteriji klasifikacije temelje se na matematičkim funkcijama, mogućnosti očuvanja svojstava i dr. Svaka od tih klasifikacija omogućuje korisno grupiranje i znanje o svojstvima transformacija kartografskih projekcija. U nastavku je prikazano nekoliko klasifikacija koje čine osnovu za bazu znanja o kartografskim projekcijama.

3. Klasifikacija

Kartografske se projekcije obično klasificiraju prema svojstvima koje čuva transformacija globusa u ravninu. Klasifikacije se temelje na obliku mreže meridijana i paralela, parametarskoj klasifikaciji ili posebnim svojstvima (Canters 2012). Te klasifikacije čine osnovu za semantičku organizaciju znanja o kartografskim projekcijama. Klasifikacija mreža meridijana i paralela temelji se na obliku linija geografskih širina i geografskih dužina koje određuju specifične obrasce koji su posljedica tipa jednadžbe upotrebljene za transformaciju. Toblerova klasifikacija prema matematičkim funkcijama najsveobuhvatnija je i najlogičnija organizacija s obzirom da se kartografske projekcije temelje na matematici (Tobler 1962); međutim, ne upotrebljava se mnogo s obzirom na to da se sastoji od apstraktnih kategorija. Malingova klasifikacija prema imenovanim geometrijskim kategorijama može se preslikati na Toblerove klase, ali ne sadrži sve matematičke forme (Maling 1973,Canters 2012). Svaka klasifikacijska shema čini jedan semantički prikaz, međutim, mogu se prikazati različite klasifikacije ako upotrijebimo osnovne semantičke koncepte kartografskih projekcija koji se nalaze u podlozi svih klasifikacija te jedan skup klasa i podklasa kao korisničko sučelje prema znanju. To još uvijek zahtijeva jednu klasifikaciju za definiranje klasa, podklasa, instanci i svojstava koje će biti upotrebljene u semantičkom prikazu. Dakle, u ovom se radu primjenjuje sustav geometrijskih klasa jer se čini da je najintuitivniji korisnicima karata te da se najčešće upotrebljava. Klase u ovoj bazi znanja uključuju azimutne, cilindrične, konusne, pseudocilindrične, prostorne (Snyder 1987) i ostale projekcije (uključujući Malingove pseudokonusne, pseudoazimutne i polikonusne klase). Potpuna hijerarhija klasa i podklasa prikazana je u Dodatku.

4. Prikaz znanja i semantika

Znanje je prikazano u obliku izjava o činjenicama i njihovu odnosu prema drugim činjenicama. Na primjer, Hrvatska je zemlja, što je činjenica koja može biti dio geografske baze znanja. Semantika uključuje značenje kao što je izraženo u lingvistici i logici. Geoprostorna semantika izražava značenje geografskih objekata, koncepata, procesa i geografskih termina i djelovanja na koje upućuju ti termini, između ostalog. Geoprostorna semantika omogućuje izradu prikaza znanja. U sljedećem odjeljku opisani su osnovni semantički koncepti povezani s geoprostornim znanjem o kartografskim projekcijama. U odjeljcima koji slijede opisana je primjena baze znanja o kartografskim projekcijama upotrebom semantičke tehnologije.

Semantička mreža

Semantička mreža pruža platformu za primjenu semantičke baze znanja. Svojom grafičkom strukturom podataka koja se temelji na trojkama, semantička mreža omogućuje pristup znanju koje mogu obrađivati ljudi i strojevi (Feigenbaum i dr. 2009). U ovom se istraživanju primjenjuju osnovna načela semantičke mreže koja su ukratko opisana u nastavku, a potpuni detalji mogu se pronaći u izvoru (W3C 2020).

RDF i trostruki model

Semantička mreža upotrebljava trostruki model Okvira opisa resursa (Resource Description Framework, RDF) za čuvanje i pristup podacima (W3C RDF 2020). Svaka trojka je pojedinačni podatkovni element strukturiran kao subjekt, predikat (svojstvo) i objekt. Subjekti trojke za izjavu o kartografskim projekcijama su klase ili jedinke. Predikati povezuju subjekte i objekte. Objekt je također klasa, jedinka ili neki drugi objekt, uključujući tekst (literals). Oblik izjave je subjekt, predikat, objekt, slično običnom jeziku. Na primjer, projekcija čuva svojstvo, gdje je projekcija subjekt, čuva je predikat, a svojstvo je objekt.

Subjekti

Subjekti su klase u kartografskim projekcijama, gdje klase predstavljaju zbirke sličnih projekcija prema određenom svojstvu. Subjekti također mogu biti jedinke. Na primjer, pojedinačne projekcije kao što je Mollweideova su subjekti. Također, autor kartografske projekcije, Karl Brandan Mollweide, još je jedan primjer jedinke koja je subjekt. Sve azimutne projekcije tvore klasu različitu od cilindričnih i konusnih projekcija (Snyder 1987). Ta matematička svojstva određuju konačan izgled karte, odakle i dolaze njihova imena. Te su klase u semantici i podklase su određene projekcije, npr. Lambertova azimutna ekvivalentna projekcija.

Predikati (Svojstva)

Cilj je svake kartografske projekcije očuvati neka svojstva prikaza Zemlje na globusu. Prema tome, logički predikat za klase kartografskih projekcija i instanci jest, ‘čuva određeno svojstvo.’ Na primjer, kartografske projekcije najčešće čuvaju površine, kuteve, udaljenost, smjer, opći izgled, loksodrome, velike kružnice kao pravce, opći oblik Zemlje kao kružnice, ovala, pravokutnika, kvadrata, romba, ili nekog od željenih oblika. Semantička izjava tada poprima oblik: subjekt čuva objekt. Objekti su tada površina, kut, udaljenost i dr. Sljedeći primjer kasnije će biti izražen u jeziku Terse RDF Triple Language (Turtle), trostrukom formatu semantičke mreže.

Mollweideova čuva površine.

Ekvidistantna cilindrična čuva udaljenosti.

Lambertova konformna konusna čuva kuteve.

Konformne projekcije čuvaju kuteve.

Treba obratiti pažnju na to da je u prva tri slučaja subjekt određena projekcija, premda njezin konačni oblik ovisi o parametrima kao što su središte projekcije i dr. U posljednjem slučaju subjekt je klasa konformnih projekcija. Budući da sve konformne projekcije čuvaju kuteve i da je Lambertova konformna konusna projekcija također konformna projekcija (podklasa konformnih projekcija), ona također mora čuvati kuteve.

Objekti

Objekti su projekcije (jedinke u semantičkom smislu), klase, zatim kutovi, tekst (literals), itd. Primjer projekcije kao objekta je: John P. Snyder kreirao je svemirsku kosu projekciju (space oblique projection), SnyderJohnP stvorio je spaceOblique. Svemirska kosa projekcija je objekt. Ta klasa semantike objekata sadrži stvari koje su logični semantički zaključak trostrukoj izjavi. Za mnoge semantičke izjave o kartografskih projekcijama, objekt je određena projekcija, svojstvo koje se čuva, npr. Mercatorova čuva kuteve; Mollweideova čuva površinu.

5. Primjer primjene u softveru Protégé

Softver Protégé Ontology (Musen 2015,Protégé 2020) primijenjen je za ontologiju klasa projekcija, podklasa, jedinki i svojstava kako bi se izradila datoteka Web Ontology Language (OWL). Protégé i izlaz OWL Protégé podržavaju opisne logičke aksiome te se stoga graf znanja može primijeniti s tom logikom za zaključivanje. Hijerarhija klasa prikazana je utablici 1. NaFigure 1 grafički su prikazane klase, podklase i popisane su jedinke u prezentaciji WebVOWL (WebVOWL 2020).

Svojstva objekata prikazana su utablici 2. Ta se svojstva upotrebljavaju za određivanje odnosa između kartografske projekcije i geometrijskog elementa i jedinki geografskih područja prikazanih utablicama 3 i4.

Svojstva za dodjeljivanje karakteristika kroz trostruki model strukturirana su kao svojstva anotacije. Ta svojstva sadrže specifikacije o projekcijama i njihovim svojstvima, kao što su definicije, formule, grafika te dodatne informacije iz mrežnih izvora uz pomoć svojstva „seeAlso“. Popis osnovnih svojstava u trenutnoj ontologiji kartografskih projekcija dan je utablici 5.

Preostale jedinke za tipove projekcija i kreatore dane su u popisima u Dodatku.

6. Primjene i rezultati

Specifični slučajevi primjene za kartografske projekcije pokazuju mogućnost za odgovaranje na specifična pitanja koja se odnose na bazu znanja. Općenito govoreći, kartografske projekcije biraju se i upotrebljavaju za očuvanje određenih svojstava s globusa. Opisane primjene strukturirane su kao upiti prema SPARQL RDF Protocol and Query Language (SPARQL). Primjena je najprije opisana na običnom jeziku, a potom s pomoću sintakse SPARQL query, a rezultat je ponovno izražen na običnom jeziku. Za konačni graf znanja kartografskih projekcija, semantička krajnja točka koja podržava upite SPARQL razvija se i omogućit će joj se pristup putem mrežne stranice Povjerenstva za kartografske projekcije (https://ica-proj.kartografija.hr/).

Primjene

Primjene koje slijede opisane su na sljedeći način: izaberi najbolju kartografsku projekciju uz određene uvjete. Rezultat svake primjene su jedna ili više kartografskih projekcija. Kad ima više kartografskih projekcija, sve se prikazuju korisniku. Računalo bira prvu projekciju na popisu, no ljudi mogu izabrati neku drugu projekciju. Također se prikazuju upiti za određivanje svojstava koje čuva određena kartografska projekcija.

1: Izaberi kartografsku projekciju koja je najbolja za kartu površinske raspodjele u srednjim geografskim širinama. Na primjer, kartiranje područja država u Sjedinjenim Američkim Državama.

Rezultat je Albersova ekvivalentna konusna projekcija.

2: Izaberi najbolju kartografsku projekciju za plovidbu cijelim svijetom

Rezultat je Mercatorova projekcija.

3: Izaberi najbolju projekciju za topografsku kartu u krupnom mjerilu.

Rezultat je poprečna Mercatorova projekcija.

4: Izaberi sve projekcije u bazi znanja koje čuvaju pravi smjer (azimute)

Rezultat su sljedeće projekcije:

ortografska

stereografska

polikonusna

5: Izaberi sve projekcije u klasi azimutnih projekcija

The results are:

stereografska

ortografska

Wagnerova VII

Airyjeva

Gilbertova

azimutna ekvidistantna

gnomonska

Aitovljeva

opća perspektivna

Hammerova

Lambertova azimutna ekvivalentna

6: Pronađi ekvivalentne projekcije prikladne za geografske širine oko ekvatora

The results are:

cilindrična ekvivalentna

EqualEarth

Eckertova IV

Eckertova VI

Mollweideova

sinusoidna

7: Učenje teorije i upotrebe kartografskih projekcija:

Za takvu primjenu, ontologija treba pristup mrežnim resursima kako bi dobila svojstva spajajući se s postojećim URL-ovima koji sadrže točne formule, tekst i grafiku za izabranu projekciju ili grupu projekcija. Kao primjer:

Opiši svojstva azimutnih projekcija.

Rezultat tog upita je poveznica na mrežni resurs:

"https://ica-proj.kartografija.hr/azimuthals-and-related-278.en.html"

Baza znanja može odgovoriti samo na upite koji se temelje na informacijama spremljenim kao trojka i odnosima među njima. Trenutno je to mali ograničeni prototip koji pokazuje primitivno znanje o kartografskim projekcijama koji može izgraditi zajednica i staviti na raspolaganje na mrežnoj stranici Povjerenstva za kartografske projekcije Međunarodnog kartografskog društva (International Cartographic Association (ICA)). Na primjer, svaka projekcija u grafu znanja sad ima svojstva ograničena na nekoliko najpoznatijih: površina, kut, smjer, udaljenost, područje kartiranja, upotreba, matematička formulacija, grafički prikaz, kreator. Budući da se osnovne jednadžbe kartografskih projekcija za transformaciju iz sfere u ravninu mogu podesiti tako da modeliraju beskonačne skupove geometrijskih i topografskih prikaza, potrebno je proširiti bazu znanja. Svojstva deformacija ovisno o klasi i pojedinoj projekciji, pokazatelje očuvanja oblika i mnoge druge moguće je dodati u bazu znanja i obogatiti znanje zajednice o kartografskim projekcijama. Također se mogu ugraditi druge klasifikacije preslikati na postojeće klase. Na primjer, Toblerove matematičke klase mogu se preslikati na postojeće klase odnosima jedan-prema-više i više-prema-jedan.

Pristup trenutnoj ontologiji i trostrukom spremištu RDF moguć je samo putem upita SPARQL queries ili ontologijskog softvera kao što je Protégé. Za širu upotrebu, potrebno je dodati prirodni jezik i sučelje za upite SPARQL. Uključivanje pitanja kompetencije na koja je moguće odgovoriti putem zaključaka i logike OWL-a također će poboljšati mogućnost i upotrebljivost baze znanja. Takva se sučelja razvijaju za upotrebu na semantičkoj mreži kako bi se omogućio lakši i širi pristup ontologijama i bazama znanja.

7. Zaključci

Razvijena je početna ontologija znanja o kartografskim projekcijama. Moguće ju je primijeniti za odabir kartografske projekcije, pedagogiju, određivanje odgovarajućih projekcija te izravne upite. Ontologija je izgrađena na temelju trojki RDF-a razvijenih u ontologijskom softveru Protégé. Konačna je ontologija datoteka OWL koju je moguće ustanoviti kao krajnju točku SPARQL-a i kojoj može pristupiti bilo tko. Konačnu verziju ontologije može se naći na mrežnoj stranici Povjerenstva za kartografske projekcije Međunarodnog kartografskog društva. Nekoliko primjena predočava potencijal takve ontologije i pruža radne primjere upita koje je moguće postaviti kako bi se dobile informacije.

Upotreba naziva tvrtki ili proizvoda isključivo je za opisne svrhe i ne podrazumijeva odobrenje od strane Vlade Sjedinjenih Američkih Država.