Equidistant, Standard and Secant Parallels

1. Introduction

Let us agree that a map projection is a mapping of a curved surface, for example the Earth's sphere or ellipsoid, into a plane. Changes that occur in such mapping are called distortions. We can differentiate distortions of length, area, and angles. If there is no distortion at any point of a line/curve we say that it is a zero distortion line or a standard line. If the same is true of a parallel, we say that it is a standard parallel. At first glance, these are familiar, generally accepted definitions, but this paper will show that a major problem exists and provides a correct, mathematically based approach.

First of all, let us remember that developing a cylindrical or conical surface into a plane is isometric mapping. In other words, all distances should remain the same after the developing procedure. Obviously, there is no reason to use a developable surface in a definition of a map projection if developing will cause additional distortions. According toDeetz and Adams (1969, pages 10-11):

There are some surfaces, however, that can be spread out in a plane without any stretching or tearing. Such surfaces are called developable surfaces and those like the sphere are called nondevelopable. The cone and the cylinder are the two well-known surfaces that are developable. Any curve drawn on the surface will have exactly the same length after development that it had before.

In the literature on map projections, the common interpretation is that the Earth's sphere or ellipsoid is first mapped onto an auxiliary developable surface, which is then developed in a plane and thus becomes a map (see, for example,Deetz and Adams 1969,Richardus and Adler 1972,Slocum et al. 2009,Clarke 2015). This approach is generally unsatisfactory. This is because the use of developable surfaces in the definition of map projections applies to only a small number of projections. If a projection is called cylindrical, it does not mean that it is a mapping onto a cylinder. Such an understanding is very common but wrong. Correct thinking is: a projection is called cylindrical if a map produced in such a projection can be bend in a cylindrical surface. The same approach holds for conical projections (Close and Clarke 1911). In addition to cylindrical and conical projections, there are many other types, such as azimuthal, pseudocylindrical, pseudoconical, conditional, and so on, which cannot be interpreted by mapping onto a cylinder or conical surface. Some attempts have been made in that direction. For example, a pseudocylindrical projection is interpreted as mapping onto an oval surface (oval, ovoid) (Clarke 2015), without noticing that such a surface is undevelopable. It does not make sense to map a sphere, which is an undevelopable surface, onto another undevelopable surface. Any surface can be transformed by animating it into any other surface. This simply confuses the essence of map projections.

More than hundred years ago, the Encyclopaedia Britannica (Close and Clarke 1911) said:

Conical projections are those in which the parallels are represented by concentric circles and the meridians by equally spaced radii. There is no necessary connexion between a conical projection and any touching or secant cone. The name conical is given to the group embraced by the above definition, because, as is obvious, a projection so drawn can be round to form a cone.

Lee (1944) remarked in The Nomenclature and Classification of Map Projections:

The projections are termed cylindric or conic because they can be regarded as developed on a cylinder or cone, as the case may be, but it is as well to dispense with picturing cylinders and cones, since they have given rise to much misunderstanding. Particularly is this so with regards to the conic projections with two standard parallels: they may be regarded as developed on cones, but they are cones which bear no simple relationship to the sphere.

The most famous cartographers, for instance Mercator and Lambert, did not use any intermediate or developable surfaces in the projections known today as the Mercator projection and Lambert conformal conical projection. The introduction of developable surfaces in the theory of map projections is artificial and unnecessary, in general. One of the contributions of this paper is the author's effort to show that the theory of map projections should be approached mathematically, not dogmatically. We advocate thinking critically about broadly accepted, but sometimes wrong, ideas and statements.

Figure 1. Illustration of standard parallels as secant parallels. Source:Deetz and Adams 1969, page 80. This is a misguided approach accompanied by the caption: "Diagram illustrating the intersection of a cone and sphere along two standard parallels". In other words, for Deetz and Adams (and many others) standard parallels and secant parallels are identical. / Slika 1. Ilustracija standardnih paralela kao presječnih paralela. Izvor:Deetz i Adams 1969, str. 80. To je pogrešno vođen pristup praćen tekstom ispod slike: "Diagram illustrating the intersection of a cone and sphere along two standard parallels". Drugim riječima, za Deetza i Adamsa (i mnoge druge) standardne paralele i presječne paralele su identične.

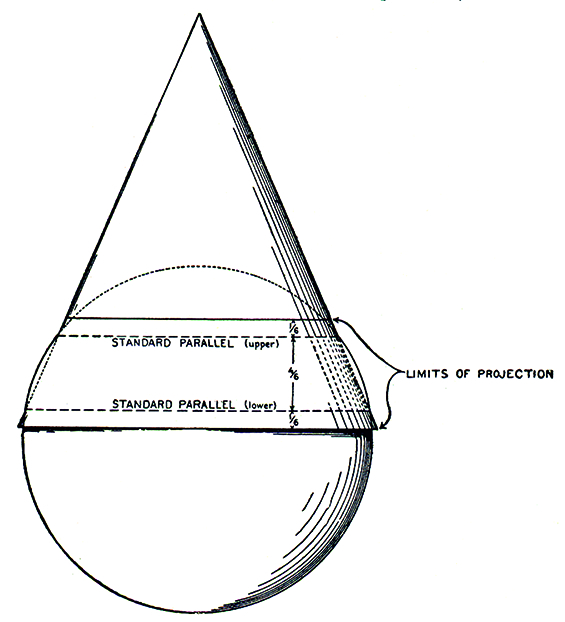
Figure 1, taken fromDeetz and Adams (1969), shows the intersection of a cone and sphere along two parallels. For Deetz and Adams (and many others), standard parallels and secant parallels are identical. This paper disagrees with such an approach. Our main goals are to propose definitions of three different types of parallels: secant, standard and equidistant, and to show that some broadly accepted facts about secant and standard parallels found in many references are incorrect and should be revised. This requires a critical approach by the reader to established customs in map projection teaching and research. In several earlier published papers (Lapaine 2015,2017a,2017b,2018,2019) it was shown that there are conical and azimuthal projections with three and more standard parallels. Obviously, this could not be explained by using the secant projections approach, and led to differentiating between standard and secant parallels. This paper goes further and introduces equidistant parallels in order to facilitate understanding and indicate the need to abandon the secant projections approach.

2. Terminology

Let us agree that the principal (linear) scale PS is the ratio of the length in the plane of projection and its origin on the surface (sphere, ellipsoid) to be projected/mapped. PS is usually indicated on maps because it determines the general degree of reduction of the length on the map. On most maps, it is usually simply called ‘scale' and is known as the map scale.

It is well known that scale changes from point to point, and at certain points usually depends on direction. This is the local scale. The local linear scale factor c is the ratio of the differential of the curve arc in the plane of projection and the differential of the corresponding curve arc on the ellipsoid or spherical surface (more details in section 5).

The local scale LS is the product of the principal scale PS and the local linear scale factor c:

LS = PS x c (1)

Since the local scale also depends on the direction, then instead of (1) it would be more correct to write

LS(α) = PS x c (α) (2)

where we denote the observed direction as α.

Length distortion is the difference between 1 and the local linear scale factor. Distortion is expressed by a number, so if c(α) = 1 for each α, then instead of the expression ‘no distortion' it would be better to say ‘distortion is equal to zero'.

This definition is found in the Multilingual Cartographic Dictionary (Borčić et al. 1977) and the Geodetic-Geoinformatic Dictionary (Frančula and Lapaine 2008):

line without distortion = Line on the map along which there is no distortion of lengths, area and angles or lines along the principal scale is preserved at all points in all directions. For perspective projections, these are the lines by which the auxiliary surface or the projection plane touches (touching parallel, touching meridian) or intersects (secant parallel, secant meridian) the sphere or ellipsoid. Remarks: (1) For the line without distortion, the term standard line is used, e.g. standard parallel (2) The point where the projection plane is tangent (touches) the surface of the ball or ellipsoid is called the touch point. See: projection, azimuthal. English: line, standard. German: Berührungslinie.

This definition actually contains two: a line without distortion and a line along which the principal scale has been preserved. Furthermore, introducing perspective projections and, in this respect, the tangent and secant parallel or meridian in the definition of a line without distortion is not good because the secant parallel does not need to be simultaneously parallel without distortion. Also, there is disagreement between languages about naming a line without distortion. For instance, in English it is called a standard line, and in German, the touch line (Berührungslinie).

In Enzyklopädischer Wörterbuch Kartographie in 25 Sprachen (Neumann 1997) we read this on page 76:

37.1 Berührungslinie = Linie auf der Kugel oder auf dem Ellipsoid [ex: Breitenkreis, Meridian etc.] in der eine für die kartographische Abbildung benutzte Hilfsab-bildungsfläche diese (a) berührt [ex: (1) Berührungsbreitenkreis, (2) Berührungs-meridian] oder (b) schneidet [ex: (3) Schnittbreitenkreis, (4) Schnittmeridian].

NB: Berührt die Hilfsabbildugsfläche einen Punkt, so spricht man vom (5) Berührungs-punkt.

E: standard line. A line on a Map Projection along which the Principal Scale obtains. (1) tangent parallel; (2) tangent meridian; (3) secant parallel; (4) secant meridian.

The terminology in the other 23 languages follows.

In the above definition in German, Berührungslinie is literally translated as touching line, and the other terms are touching parallel, touching meridian, secant parallel and secant meridian. The auxiliary surface (Hilfsabbildugsfläche) has a decisive role, while distortion is not mentioned at all!

In the English definition in same dictionary, a standard line is "a line in map projection along which the scale is equal to the principal scale". The auxiliary surface is not mentioned explicitly, but the terms tangent parallel, tangent meridian, secant parallel and secant meridian occur. In French, it is the "contact line or intersection with auxiliary projection surface", and in Russian the "zero distortion line, i.e. a line on the map where the principal scale at each point is preserved". The same understanding appears in the Portuguese definition.

In ESRI's Web Dictionary (ESRI 2017) we find this definition: "Standard line = [map projections] A line on a sphere or spheroid that has no length compression or expansion after being projected; usually a standard parallel or central meridian". Thus, only what happens along the line is important, not around it, although it is known that the linear scale factor or scale at each point generally depends on the direction (Tissot indicatrix).

Snyder and Voxland (1989) say this of perspective conical projection. " Scale. True along one or two chosen standard parallels, which may be on the same side of or both sides of the Equator... Distortion. Free of distortion only along the one or two standard parallels." These statements are incorrect because a simple perspective conical projection cannot have two standard parallels.

From the above, we can conclude that there is terminological confusion. The standard line and secant line are not uniformly defined terms. Confusion appears to arise from misunderstandings and results in the acceptance of unfounded assertions. We will attempt to resolve this confusion in this paper.

The same idea can be applied to the transverse and oblique aspects of both cylindrical and conical projections.

In order to be mathematically correct in all the sections that follow, we refer to published papers byLapaine 2015,2017a,2017b,2018,2019.

3. Points, Lines and Areas with Zero Distortions

Let us say that at some point the distortion is zero if the local linear scale factor is equal to 1, i.e. if it is

c(α)=1, for each α ∈ [0,2π], (3)

where c(α) is defined in (4)

where E, F and G are coefficients in the first differential form of the map projection. We use a sphere intentionally to facilitate understanding and to shorten derivations.

Note there is a difference between zero and none. Zero is a number, while none is not. Due to the fact that distortion is a number, it would be preferably to use "zero distortion" instead of "no distortion".

The requirement (3) is obviously equivalent to the condition

c_min = c_max = 1 (5)

that tell us it is a Tissot indicatrix transformed into the unit circle. Let us emphasize that in (3) the term "for each α ∈ [0,2π]" is important, and it is not enough that the written property is valid for only one α. In other words, in order for an ellipse to be a circle, it is necessary for all of its radiuses to be mutually equal or, in the same way, for the semi-axes to be of the same length. It is not enough for one semi-axis of the ellipse to be equal to 1 so that the ellipse is the unit circle. This should be clear to everyone, although it can be inferred from the introductory chapter that it is not.

In a special case, when F = 0, the expressions (5) can be written like this

h = k = 1, (6)

where h and k are local linear scale factors along meridian, and along parallel, respectively.

Let us introduce for the sake of abbreviation:

a = c_max,b = c_min (7)

Let us first note that a > 0 and b > 0 is always true.Table 1 shows all possible cases when a=1, b=1 or a=b=1. This is very simple but new in the theory of map projections:

(1,1)

If at some point a = 1, we can say that this point is locally equidistant in the direction of maximum local linear scale factor.

(1,2)

If at some point b = 1, we can say that this point is locally equidistant in the direction of minimal local linear scale factor.

(1,3)

If at some point a = b = 1, we can say that this is a point with zero distortion, a zero-distortion point or a standard point.

(2,1)

If at all points of a line a = 1, then it is not generally a line with zero distortion, but we can say that this line is equidistant in the direction of maximum local linear scale factor.

(2,2)

If at all points of a line b = 1, then it is not generally a line with zero distortion, but we can say that this line is equidistant in the direction of minimal local linear scale factor.

(2,3)

If at all points of a line a = b = 1, then it is a line with zero distortion, a zero-distortion line or a standard line.

(3,1)

If at all points of an area a = 1, then we can say that this area is equidistant in the direction of maximum local linear scale factor.

(3,2)

If at all points of an area b = 1, then we can say that this area is equidistant in the direction of minimal local linear scale factor.

(3,3)

The expression a = b = 1 cannot be true at all points of a two-dimensional area on the map, as this would mean map projection without distortion. Leonhard Euler first proved that this was not possible (Euler 1777).

Table 1. All possibilities of standard points and lines vs. equidistant points and lines in map projections. If a = b = 1, we have a standard point or line. If a = 1 or b = 1, we have an equidistant point, line or area. The case (3,3) is not possible.

In a special case, when F = 0, then we can use h and k instead of a and b.

If at all points of a meridian we have h = 1, then it is not generally a zero-distortion meridian, but a meridian along which, or in the direction of which, the distortion is zero. We can say that the meridian is mapped equidistantly.

If at all points of a mapped area h = 1, then we say that the map projection is equidistant along meridians. For example, normal aspect of the Postel projection is azimuthal projection equidistant along all meridians.

If at all points of a parallel we have k = 1, then it is not generally a zero-distortion parallel, but a parallel along which, or in the direction of which, the distortion is zero. We can say that the parallel is mapped equidistantly.

If at all points of a mapped area k = 1, then we say that the map projection is equidistant along parallels. For example, normal aspect of the orthographic projection is azimuthal projection equidistant along parallels.

If at all points of a meridian we have h = k = 1, then it is a zero-distortion meridian, or the distortion of that meridian is zero in all directions, i.e. this is a standard meridian.

If at all points of a parallel we have h = k = 1, then it is a zero-distortion parallel, or the distortion of that parallel is zero in all directions, i.e. this is a standard parallel.

4. Equidistant, Standard and Secant Parallels

Normal aspect cylindrical projections of a sphere are mappings defined by the formula

x = R_n(λ-λ)₀, y = Rf(φ), (8)

where

, λ ∊ [-π ,π], constants are n>0, R>0 and λ₀ ∊ [-π ,π], function y = Rf(φ) is piecewise continuous, differentiable, monotone increasing and odd. As in any map projection, x and y are coordinates of a point in a rectangular (mathematical, right oriented) plane coordinate system. As anyone can see, this is about mapping into the plane, not onto the surface of a cylinder. For such mapping,

and the first differential form is

The local linear scale factor squared for a mapping a sphere by using normal aspect cylindrical projection (8) is

Local linear scale factors along a meridian and a parallel, respectively are

For normal aspect cylindrical projections, along standard parallels with latitudes

φ±φ₁ it should be h(φ₁) = k(φ₁) = 1, (13)

or considering (12) and (9)

and

From the formula (15) and the properties of trigonometric function cosine we can conclude that if the latitude of the standard parallel is φ ₁, then it should be -φ ₁, too. The number of standard parallels in normal aspect cylindrical projections we can conclude based on the relations (14) and (15).

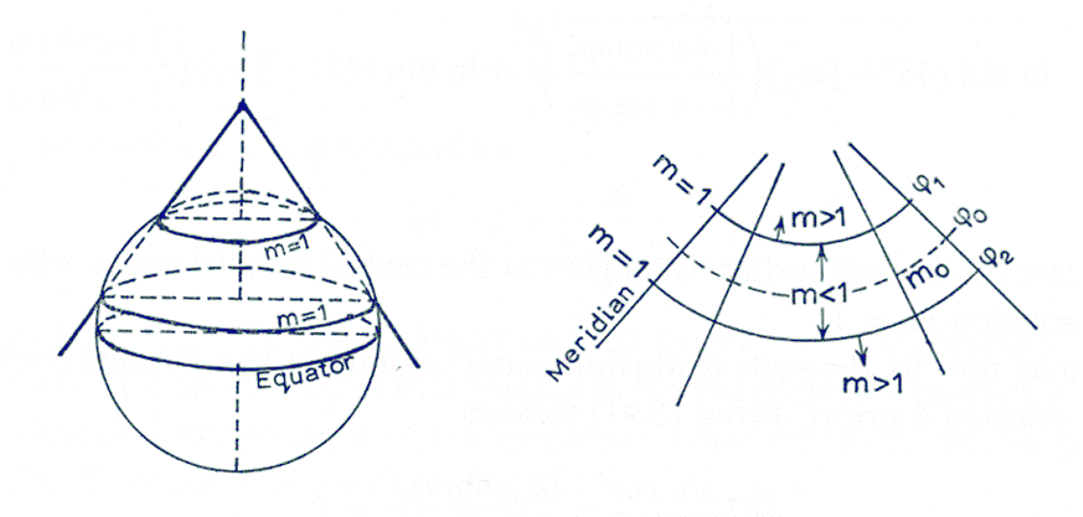
If 0<n<1 then two standard parallels exist (φ₁ and -φ₁), if it is also

If n = 1 then only one standard parallel (φ₁ = 0) can exist, the Equator, providing that it is

If n>1 then there is no φ₁ for which (15) holds, i.e. there is no standard parallel at all.

Let φ and -φ be the latitudes of two parallels mapped by normal aspect cylindrical projection (8). The vertical distance between these two parallels on the sphere is 2 Rsinφ, and the distance between their images in the plane of projection (seeFig 2) is 2y( φ). It is clear that 2 y( φ) = 2Rsinφ, i.e. y( φ) = Rsin φ is not true in general. It is true for the Lambert equal-area projection only. Thus, bending a map made in the normal aspect cylindrical projection onto a cylindrical surface and then putting it in a particular position with the sphere generally makes no sense. In other words, map projection and folding or unfolding of the cylindrical surface are two completely different actions. Since secant parallels do not have any particular property in terms of distortion distribution, we conclude that the use of cylindrical surfaces in the theory of map projections generally makes no sense and can lead to wrong conclusions about the identities of secant and standard parallels (Fig 3). The use of cylindrical surfaces makes sense in perspective projections on a cylinder only, but such projections are rarely applied.

Figure 2. Illustration showing that the distance between two parallels symmetrical to the Equator and the distance between their images in the plane of projection are different in general. It follows that equidistant or standard parallels can not be secant parallels because bending is an isometry, i.e. squeezing or stretching is not allowed. / Slika 2. Ilustracija koja pokazuje da udaljenost između dviju paralela simetričnih s obzirom na ekvator i udaljenost između njihovih slika u ravnini projekcije općenito nisu jednake. Odatle slijedi da ekvidistantne ili standarnde paralele ne mogu biti istodobno presječne paralele jer je savijanje izometrija, tj. stiskanje ili razvlačenje nije dopušteno.

Figure 3. The usual erroneous illustration: standard parallels are at the same time secant parallel in normal aspect cylindrical projection (Mercator 2009). We have proved that this is impossible. The illustration is an illusion. / Slika 3. Uobičajena pogrešna ilustracija: standardne paralele su istodobno presječne paralele u uspravnom aspektu cilindrične projekcije (Mercator 2009). Dokazali smo da je to nemoguće. Ta ilustracija je iluzija.

To summarize about cylindrical projections given by (8):

Two parallels (φ₁ and -φ₁) are equidistant parallels if

n = cosφ ₁ (16)

Two parallels (φ₁ and -φ₁) are standard parallels if holds (16) and

Two parallels (φ₁ and -φ₁) are secant parallels if the distance between these two parallels on the sphere equals the distance between their images in the plane of projection:

f (φ₁) = sinφ₁. (18)

Two examples on cylindrical projections follow.

Let the normal aspect cylindrical projection be defined as

λ ∊ [-π ,π], where the constants are R>0 and λ₀ ∊ [-π ,π].

Since f(φ) = φ and

we can conclude that all meridians are mapped equidistantly (h = 1) in this projection. From the condition

, which is easy to derive from (15) and (19), we see that the parallels that correspond to latitudes

are also mapped equidistantly

Since all the meridians in this projection are mapped equidistantly, the two equidistantly mapped parallels are also standard parallels

The distance between two parallels that corresponds to latitudes φ and -φ on a sphere is 2 Rsin φ (seeFig. 2). If

then the distance between these two parallels on the sphere is

The distance of their images in the plane of projection is 2y(φ) = 2R(φ), which for

amounts

Thus, by bending the map into the cylindrical surface and placing the cylinder so that its axis fits in with the straight line connecting the North and South Poles, and putting the image of the Equator in the equatorial plane, it is impossible for the secant parallels coincide with the equidistant (in this case also standard) parallels. Thus, we have shown that secant and standard parallels in cylindrical projections generally cannot be identical.

The Behrmann projection equations reads (Lapaine 2018)

For that projection

so we have

It is immediately apparent that this projection is equal-area because it is hk = 1 for any φ.

Snyder and Voxland (1989) write that the Behrmann Projection is true along latitude 30° and that it is a projection on a cylinder secant at ±30° (True along latitudes ±30°, projection onto a cylinder secant at ±30° ). The standard parallels of the Behrmann projection correspond to latitudes ±30°. The distance between these parallels on the sphere with radius R is obviously R. In the plane of Behrmann's projection the distance between their images is

which is obviously different from R. This means that a map cannot be made in Behrmann's projection by developing into a plane the Behrmann cylindrical surface that cuts the sphere along the parallels of ±30° latitudes. Conversely, a map made in Behrman's projection cannot bend into a cylindrical surface that will intersect the sphere along the parallels of ±30° latitudes. Identifying the equidistant or standard parallel and the parallel in which the cylindrical surface intersects the Earth's sphere is obviously not a valid procedure (Lapaine 2018).

A conic projection is mapping defined by the formulae

ρ = Rf(φ), θ = n(λ-λ₀) (23)

where

λ ∊ [-π ,π], the constants are n>0, R>₀ and λ₀ ∊ [-π ,π],

and the function ρ = Rf(φ) is continuous, with positive values and monotone decreasing, or monotone increasing, and ρ and θ are coordinates of a point in the polar coordinate system in the plane. As can be seen, this is about mapping into the plane, not onto a conical surface. For such mapping we have

and the first differential form

The square of the local linear scale factor of normal aspect conic projection (23) is

From (26) we can read the local linear scale factor along the meridians and parallels, respectively

The minus sign in the formula for h was chosen because functions ρ and f are monotone decreasing by hypothesis. If these functions are monotone increasing, then φ should be replaced by -φ in the derivation that follows.

In normal aspect conic projections, F = 0 and (27) holds.

If for any

it is

then all meridians are mapped equidistantly. If for some

it is

then parallels corresponding to these latitudes are mapped equidistantly.

Along a standard parallel φ = φ ₁ it should be true that

h(φ ₁) = k(φ ₁) = 1, (28)

that is,

and

We cannot make any conclusions about the number of standard parallels in normal aspect conical projections as we could with cylindrical ones. This is because for the given n there are infinitely many continuous functions ρ = Rf(φ), which are differentiable with positive values and monotone decreasing for

, and which satisfy conditions (29) and (30) for several different values of the latitudes

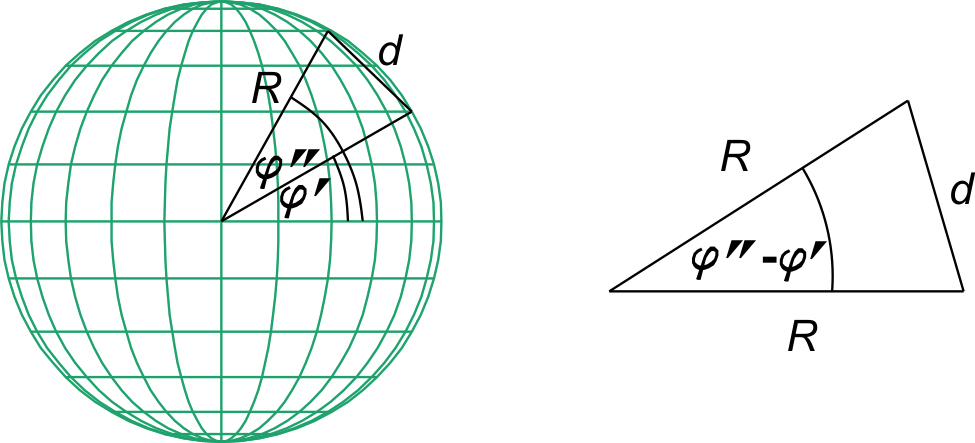
Let us note two parallels on the sphere with radius R, and let φ' and φ'' be the corresponding latitudes 0 ≤ φ'<φ'' ≤ 90°. The shortest distance d between these two parallels (Fig. 4) equals

The distance between their images on the map will be

However, the equality

is not true in general. Thus, it is not applicable to parallels mapped equidistantly and for standard parallels. This means that bending a map produced in the normal aspect conical projection into a conical surface and placing it in a particular position related to the sphere generally makes no sense. In other words, map projection and developing the conical surface into a plane are two quite different actions. Since secant parallels do not have any particular property in terms of distortion distribution, we conclude that the use of conical surfaces in the theory of map projections generally makes no sense and can lead to wrong conclusions about the identities of secant and standard parallels.

Figure 4 The distance d between two parallels given by their latitudes φ' and φ”. / Slika 4 Udaljenost d između dviju paralela zadanih njihovim geografskim širinama φ' i φ''.

To summarize about conical projections given by (23) and two parallels (0 ≤ φ' < φ" ≤ π/2) :

Two parallels (φ' and φ'') are equidistant parallels if

nf(φ') = cos φ' and nf(φ'') = cos φ''. (34)

Two parallels (φ' and φ'') are standard parallels if holds (34) and

df/dφ (φ') = 1 and df/dφ (φ'') = 1 (35)

Two parallels (φ' and φ'') are secant parallels if the distance between these two parallels on the sphere equals the distance between their images in the plane of projection:

f(φ')-f(φ") = 2sin sin(φ"-φ')/2 (36)

Three examples on conical projections follow.

4.2.1. Example 3

Let the normal aspect conical projection be defined as:

where

λ ∊ [-π ,π], R>0 and λ₀ ∊ [-π ,π]. Since

and

we conclude that all meridians are mapped equidistantly.

The condition (34) implies that two parallels corresponding to latitudes 0° and 60° are mapped equidistantly

Since all meridians in this projection are mapped equidistantly (h(φ) = 1 for all φ), the two equidistantly mapped parallels are standard parallels.

The distance d between two parallels with latitudes φ' and φ'' on the sphere is given by (36). If φ' = 0° and φ'' = 60°, then the distance between them on the sphere is 2Rsin30° = R. The distance between their images in the plane of projection is

, and for φ' = 0° and φ'' = 60° this is

which is different from R. Thus, by bending the map into the conical surface and placing the cone so that its axis coincides with the straight line connecting the North and South Poles, it is not possible to obtain secant parallels identical with the standard parallels. Thus, we have shown that secant and standard parallels in conical projections generally cannot be identical.

In their well-known book on map projections, Richardus and Adler (1972, page 94) interpret Lambert's conformal conical projection with two standard parallels and illustrate the derivation by depicting a cone that intersects the ellipsoid into two parallels (Fig. 5). Richardus and Adler wanted to show that these parallels were secant and standard parallels, but this cannot be true if we accept the definitions of secant and standard parallels recommended in this paper. Let us prove this using a simple example of a sphere of radius 1 and Lambert's conformal conical projection with two standard parallels corresponding to the latitudes φ' = 0° and φ'' = 60°.

Figure 5. Illustration of standard parallels as parallels in which the conical surface intersects the Earth's ellipsoid. Source:Richardus and Adler (1972, page 94) . This is generally a misguided approach and is accompanied by the inaccurate statement, "This is the Lambert conical conformal projection with two standard parallels. The cone intersects the ellipsoid at these parallel circles". Figure without red cross was taken fromRichardus and Adler (1972, page 94) , and it is an illusion. Red cross was used to stress that something is wrong with the figure. After looking at the figure and reading the text, it is expected that the reader will be able to distinguish between fact and illusion. / Slika 5. Ilustracija standardnih paralela kao paralela u kojima konusna ploha siječe Zemljin elipsoid. Izvor:Richardus i Adler (1972, str. 94) . To je općenito pogrešan pristup koji je popraćen netočnom tvrdnjom: "To je Lambertova konusna konformna projekcija s dvije standardne paralele. Konus siječe elipsoid u tim kružnim paralelama". Slika bez crvenih crta preuzeta je iz knjigeRichardusa i Adlera (1972, str. 94) , i to je jedna obmana. Precrtano crvenim je upotrijebljeno da bi se istaknulo da na toj slici nešto nije kako treba. Nakon gledanja slike i čitanja teksta, čitatelj bi trebao razlikovati činjenicu od iluzije.

First of all, there is no intermediate conical surface in the Lambert conformal conic projection. This is evident from Lambert's original work or the English translation (Lambert 1772).

If a map in the Lambert conic conformal projection has two standard parallels (right-hand part ofFig. 5), then it is not possible to bend it into a conical surface which will cut the earth's sphere along these two parallels (left-hand part ofFig. 5). Though this may surprise some people, it will be proved in this example.

In order for the conical projection to be conformal, it must be true that

h = k, (38)

where h and k are defined in (27). From there, because R =1, it follows

and then

from where, after integration, we get

that is,

where C is a constant of integration.

Let φ' = 0° and φ'' = 60° be two standard parallels. The conditions for standard parallels

and

form a system of two equations with two unknowns, n and C, which can be transformed into

and

from where it follows that

and

If we now substitute values φ' = 0° and φ'' = 60° we will get

The distance between the images of standard parallels with latitudes φ' = 0° and φ'' = 60° in the plane of Lambert conformal conical projection equals

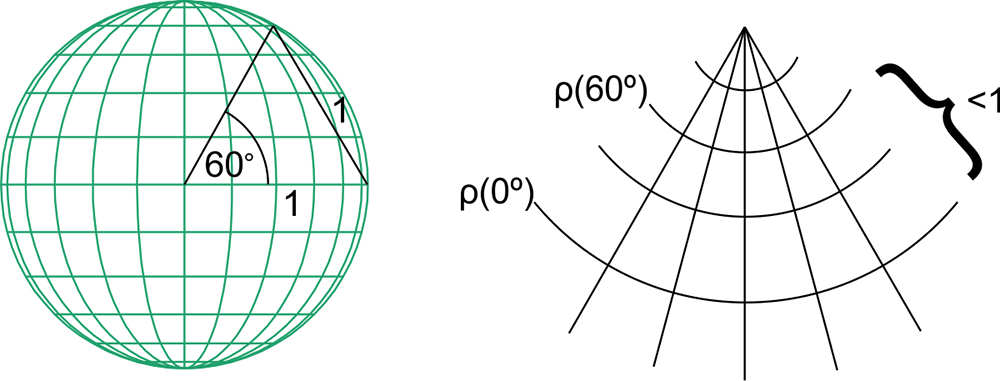
Let us bend the map into a conical surface and place the cone so that its axis coincides with the straight line connecting the North and South Poles on the sphere. It is not possible to obtain secant parallels identical with the standard parallels, because the shortest distance between standard parallels on the sphere measured along a straight line connecting the two parallels is equal to 1 (Fig. 6). Bending (and developing) is isometry, that is, transformation that preserves distances.

If we bend a map made in the normal aspect conical projection into a conical surface and then try putting it in a particular position with the sphere, standard parallels in the projection will not coincide with standard parallels on the sphere. In other words, map projection and folding or unfolding of the conical surface are two completely different actions.

We have proved that secant parallels are not standard parallels, in general.

Figure 4 The distancFigure 6. In conical conformal projection of a unit sphere the distance between two standard parallels latitudes φ 1=0° and φ 2=60° equals 1 on the sphere, and less then 1 in the plane of projection.e d between two parallels given by their latitudes φ' and φ”. / Slika 6. U Lambertovoj konusnoj konformnoj projekciji jedinične sfere udaljenost između dviju standardnih paralela kojima odgovaraju geografske širine φ1= 0° and φ2= 60° jednaka je 1 na sferi, a manja je od 1 u ravnini projekcije

Snyder (1993), in his famous book Flattening the Earth, says this on page 123, "Like the central cylindrical projection described earlier, a conic projection may be developed by geometrically projecting the globe from its centre onto a cone either tangent at one parallel or secant at two. It is so elementary that there seems to be no formal origin of it ...". "For two standard parallels φ ₁ and φ ₂, the polar coordinates are as follows:

, θ = λsin(φ₀),

where

... For the tangent form with one standard parallel, φ₁ may be equated to φ₁. If the standard parallels favour the northern hemisphere, only part of the southern hemisphere can normally be shown". Snyder was apparently convinced that there was a gnomonic or central perspective projection on a cone with two standard parallels. He did not check the truth of this and accepted it as a fact, though it is erroneous. Here is the evidence!

The local linear scale factor along the meridian in a normal aspect conical projection is calculated according to (27)

For a function ρ = ρ(φ) defined by (49) one can easily calculate

and then

from where

which is different from 1, unless φ₁ = φ₂. We have shown that a simple gnomonic perspective projection on a conical surface cannot have two standard parallels. In other words, if the conical surface intersects the sphere at two parallels, these two parallels cannot be standard parallels in the gnomonic perspective projection.

5. Conclusion

We argue that the explanation of cylindrical and conical projections as projections on cylindrical or conical surfaces is not a good approach, because it leads to misunderstanding some projection properties. Furthermore, standard and secant parallels are often considered identical, but this paper has shown that broadly accepted facts about secant and standard parallels found in many references are incorrect and should be revised. This requires a critical approach to established customs in teaching and researching map projection. In several previously published papers it was shown that conical and azimuthal projections existed with three and more standard parallels. Obviously, this could not be explained by using the secant projections approach and led to distinguishing between standard and secant parallels. The equidistant projections are known in the theory of map projections. The paper introduces equidistance in a broader sense. Equidistance is defined at a point, along a line and in an area. This allowed three types of parallels to be defined: secant, standard and equidistant. Explicit conditions for equidistant, standard and secant parallels are given for cylindrical and conical projections. Theoretical assertions are illustrated by appropriate examples.

In order to prevent misunderstandings, we suggest avoiding the use of developable surface as intermediate surfaces and distinguishing equidistant, standard and secant lines in the theory of map projections and teaching it.

1. Uvod

Prihvatimo da je kartografska projekcija preslikavanje zakrivljene plohe, primjerice Zemljine sfere ili elipsoida, u ravninu. Promjene koje se događaju pri takvom preslikavanju nazivaju se distorzije. Razlikuju se distorzije duljina, površina i kutova. Ako nema distorzija u svakoj točki neke linije/krivulje kažemo da je to linija s distorzijom nula ili standardna linija. Ako to vrijedi za paralelu, kažemo da je to standardna paralela. Na prvi pogled to su poznate, opće prihvaćene definicije, no u ovom članku ćemo pokazati da nije tako i dati korektan, matematički utemeljen pristup.

Ponajprije, prisjetimo se da je razvijanje cilindrične ili konusne plohe izometrijsko preslikavanje. Drugim riječima, sve udaljenosti moraju ostati nepromijenjene nakon razvijanja tih ploha u ravninu. Očito je da ne bi imalo smisla koristiti se razvojnim plohama pri definiranju kartografskih projekcija kad bi razvijanje donosilo dodatne distorzije.

Prema toDeetzu i Adams (1969, str. 10-11):

Postoje neke plohe koje se mogu ispružiti u ravninu bez rastezanja ili trganja. Takve se plohe nazivaju razvojnim plohama, a one poput sfere zovu se nerazvojnima. Konus i cilindar su dvije dobro poznate plohe koje su razvojne. Svaka krivulja nacrtana na takvoj plohi imat će istu duljinu nakon razvijanja kao što je imala prije.

U literaturi o kartografskim projekcijama uobičajena je interpretacija da se Zemljina sfera ili elipsoid najprije preslikavaju na pomoćnu razvojnu plohu, koja se zatim razvija u ravninu pa tako nastaje karta (vidi npr.Deetz i Adams 1969,Richardus i Adler 1972,Slocum i sur. 2009,Clarke 2015). Takav je pristup općenito nezadovoljavajući. Naime upotreba razvojnih ploha u definiciji kartografske projekcije primijenjuje se samo na mali broj projekcija. Ako se projekcija naziva cilindričnom to ne znači da je riječ o preslikavanju na cilindar. Takvo razumijevanje je vrlo često, no pogrešno. Ispravno razmišlajnje je ovo: projekcija se naziva cilindričnom ako se karta izrađena u takvoj projekciji može saviti u cilindričnu plohu. Analogno vrijedi za konusne projekcije (Close i Clarke 1911). Osim cilindričnih i konusnih projekcija postoje mnoge druge, kao što su azimutne, pseudocilindrične, pseudokonusne, uvjetne itd., koje se ne mogu interpretirati kao preslikavanja na cilindričnu ili konusnu plohu. Doduše, postoje neki pokušaji u tom smjeru. Na primjer, pseudocilindrična projekcija se interpretira kao preslikvanje na ovalnu plohu (oval, ovoid) (Clarke 2015), ali se ne uočava da takva ploha nije razvojna. Nema smisla preslikati sferu koja je nerazvojna ploha, na drugu nerazvojnu plohu. Svaka se ploha može transformirati animacijom na bilo koju drugu plohu. To stvara pomutnju u bit kartografskih projekcija.

Prije više od 100 godina objavljeno je u Encyclopaediji Britannici (Close i Clarke 1911):

Konusne projekcije su takve projekcije kod kojih su paralele prikazane kao koncentrične kružnice, a meridijani kao jednako razmaknuti radijusi. Nije nužna veza između konusne projekcije i dodirnog ili presječnog konusa. Ime konusne dano je skupini koja je obuhvaćena gornjom definicijom, jer, kao što je očito, projekcija koja je tako nacrtana može se saviti u oblik konusa.

Lee (1944) je primijetio u The Nomenclature and Classification of Map Projections:

Projekcije se nazivaju cilindrične ili konusne jer se mogu doživjeti kao razvoji cilindra ili konusa, što može biti, ali isto tako je dobro i odustati od prikazivanja cilindara i konusa jer su oni stvorili mnogo nesporazuma. Posebno je to tako s obzirom na konusne projekcije s dvije standardne paralele: one se mogu shvatiti kao razvijene na konusima, no postoje konusi koji nemaju nikakvu jednostavnu relaciju sa sferom.

Najslavniji kartografi, npr. Mercator i Lambert, nisu se koristili nikakvim posrednim ili razvojnim plohama za projekcije koje danas poznajemo kao Mercaorovu projekciju ili Lambertovu konformnu konusnu projekciju. Uvođenje razvojnih ploha u teoriju kartografskih projekcija je umjetno i općenito nepotrebno. Jedan od doprinosa ovog članka je nastojanje autora da pokažu da kartografskim projekcijama treba pristupiti matematički, a ne dogmatski. Zastupamo potrebu kritičkog mišljenja o široko prihvaćenim, no ponekad pogrešnim, idejama i tvrdnjama.

2. Nazivlje

Dogovorimo se da je glavno (linearno) mjerilo PS omjer duljine u ravnini projekcije i njezinog originala na plohi (sfera, elipsoid) koja se projicira/preslikava. PS se obično zapisuje na karti jer određuje opći stupanj smanjivanja duljina prikazanih na karti. Na većini karata ono se obično naziva "mjerilo", a poznato je kao mjerilo karte.

Dobro je poznato da se mjerilo mijenja od točke do točke, a u pojedinoj točki obično ovisi i o smjeru. To je lokalno mjerilo. Faktor lokalnog mjerila duljina c je omjer diferencijala luka krivulje u ravnini projekcije i diferencijala odgovarajuće glika krivulje na elipsoidnoj ili sfernoj plohi (više detalja u poglavlju 5).

Lokalno mjerilo LS je produkt glavnog mjerila PS i lokalnog linearnog faktora mjerila c:

LS = PS x c (1)

Budući da lokalno mjerilo također ovisi o smjeru, umjesto (1) bilo bi bolje pisati

LS(α) = PS x c (α) (2)

gdje smo promatrani smjer označili s α.

Distorzija duljina je razlika između 1 i faktora lokalnog mjerila duljina. Dakle ona se izražava brojem, tako da ako je c(α) = 1 za svaki α, tada je umjesto izraza "bez distorzije" bolje reći "distorzija jednaka nuli".

Ova definicija može se naći u Multilingual Cartographic Dictionary (Borčić i sur. 1977) i u Geodetsko-geoinformatičkom rječniku (Frančula and Lapaine 2008):

linija bez deformacija = linija na karti uzduž koje nema deformacija duljina, površina i kutova ili linija uzduž koje je sačuvano glavno mjerilo u svim točkama i svim smjerovima. Za perspektivne projekcije, to su linije u kojima pomoćna ploha ili ravnina projekcije dodiruje (dodirna paralela, dodirni meridijan) ili siječe (presječna paralela, presječni meridijan) sferu ili elipsoid. Napomene: (1) Za liniju bez deformacija upotrebljava se naziv standardna linija, npr. standardna paralela (2) Točka u kojoj je ravnina projekcije tangencijalna (dodiruje) plohu kugle ili elipsoida zove se dodirna točka. Vidi: projekcija, azimutalna. Engleski: line, standard. Njemački: Berührungslinie.

Ta definicija zapravo sadrži dvije definicije: linije bez distorzije i linije uzduž koje je sačuvano glavno mjerilo. Nadalje, uvođenje perspektivnih projekcija i, s tim u vezi, dodirnih i presječnih paralela ili meridijana u definiciju linije bez distorzije nije dobro jer presječne paralele obično nisu paralele bez distorzije. Osim toga, postoji i neslaganje u jezicima za imenovanje linije bez distorzije. Na primjer, na engleskom je to standard line, a na njemačkom dodirna linija Berührungslinie.

U Enzyklopädischer Wörterbuch Kartographie in 25 Sprachen (Neumann 1997) na str. 76 možemo pročitati ovo:

37.1 Berührungslinie = Linie auf der Kugel oder auf dem Ellipsoid [ex: Breitenkreis, Meridian etc.] in der eine für die kartographische Abbildung benutzte Hilfsab-bildungsfläche diese (a) berührt [ex: (1) Berührungsbreitenkreis, (2) Berührungs-meridian] oder (b) schneidet [ex: (3) Schnittbreitenkreis, (4) Schnittmeridian].

NB: Berührt die Hilfsabbildugsfläche einen Punkt, so spricht man vom (5) Berührungs-punkt.

E: standard line. A line on a Map Projection along which the Principal Scale obtains. (1) tangent parallel; (2) tangent meridian; (3) secant parallel; (4) secant meridian.

Slijede nazivi na ostala 23 jezika.

U prethodnoj definiciji na njemačkom, Berührungslinie doslovno prevedeno znači dodirna linija, a ostali nazivi su dodirna paralela, dodirni meridijan, presječna paralela i presječni meridijan. Pomoćna ploha (Hilfsabbildugsfläche) ima odlučujuću ulogu, a distorzija se uopće ne spominje!

U engleskoj definiciji u istom rječniku standardna linija je "linija u kartografskoj projekciji uzduž koje je mjerilo jednako glavnom mjerilu". Pomoćna ploha se ne spominje eksplicitno, ali se pojavljuje nazivi tangencijalna paralela, tangencijalni meridijan, presječna paralela i presječni meridija. Na francuskom to je "linija dodira ili presjeka s pomoćnom projekcijskom plohom", a na ruskome "linija distorzije nula, tj. linija na karti gdje je glavno mjerilo u svakoj točki sačuvano". Slično razumijevanje pojavljuje se u protugalskoj definiciji.

U ESRI-jevu rječniku na webu (ESRI 2017) nalazimo ovu definiciju: "Standardna linija = [kartografske projekcije] linija na sferi ili sferoidu čija duljina se neće sažeti ili rastegnuti nakon što je projicirana; obično je to standardna paralela ili srednji meridijan". Dakle, važno je samo ono što se događa uzduž linije, a ne oko nje, premda je poznato da faktor lokalnog mjerila duljina i mjerilo u svakoj točki ovise od smjeru (Tissotova indikatrisa).

Snyder i Voxland (1989) kažu ovo o perspektivnoj konusnoj projekciji: "Mjerilo. Istinito je uzduž jedne ili dviju odabranih standardnih paralela, koje mogu biti s iste strane ekvatora ili s obiju strana ... Distorzija. Distorzije nema samo uzduž jedne ili dviju standardnih paralela." Te tvrdnje nisu točne jer jednostavna perspektivna konusna projekcija nemože imati dvije standardne paralele.

Na temelju navedenoga možemo zaključiti da postoji terminološka zbrka. Standardna linija i presječna linija nisu jednoznačno definirani nazivi. Čini se da zabuna proizlazi iz nesporazuma i rezultira prihvaćanjem neutemeljenih tvrdnji. U ovom članku nastojat ćemo razriješiti tu zbrku.

Ista ideja može se primijeniti na poprečne i kose aspekte cilindričnih i konusnih projekcija.

Da bismo bili matematički korektni u svim poglavljima koja slijede pozivamo se na Lapaineove objavljene članke2015,2017a,2017b,2018,2019.

3. Točke, linije i površine s distorzijama jednakima nuli

Reći ćemo da je u nekoj točki distorzija jednaka nuli ako je faktor lokalnog mjerila duljina jednak 1, tj. ako je

c(α)=1, za svaki α ∈ [0,2π], (3)

gdje je c(α) definirano u (4)

gdje su E, F i G koeficijenti prve diferencijalne forme kartografske projekcije. Namjerno smo upotrijebili sferu kako bismo olakšali razumijevanje i skratili izvode.

Uočimo da postoji razlika između nula i ništa. Nula je broj, a ništa nije. Zbog činjenice da je distorzija broj, bolje je reći "distorzija je nula" umjesto "nema distorzije".

Zahtjev (3) je očito ekvivalentna umjetu

c_min = c_max = 1 (5)

koji nam govori da je Tissotova indikatrisa (elipsa) transformirana na jediničnu kružnicu. Naglasimo da je u (3) naziv "za svaki α ∈ [0,2π]" važan, i da nije dovoljno da navedeno svojstvo vrijedi za smamo jedan . Drugim riječima, da bi elipsa bila kružnica, nužno je da svi njezini polumjeri budu međusobno jednaki, ili da njezine poluosi budu jednako dugačke. Nije dovoljno da jedna poluos elipse bude jednaka 1 pa da elipsa bude jedinična kružnica. To bi trebalo biti jasno svakome, premda se iz uvoda u ovaj članak može zaključiti da nije tako.

U posebnom slučaju kad je F = 0, izraz (5) može se napisati ovako

h = k = 1, (6)

gdje su h i k faktori lokalnog mjerila duljina uzduž meridijana, odnosno paralele.

Uvedimo radi kraćeg pisanja oznake:

a = c_max,b = c_min (7)

Najprije uočimo da je a>0 i b>0 uvijek istina.Table 1 pokazuje sve moguće slučajeve kad je a=1, b=1 ili a=b=1. To je vrlo jednostavno, ali novo u teoriji kartografskih projekcija:

(1,1)

Ako je u nekoj točki a = 1, možemo reći da je ta točka lokalno ekvidistantna u smjeru makimalnog faktora lokalnog mjerila duljina.

(1,2)

Ako je u nekoj točki b = 1, možemo reći da je ta točka lokalno ekvidistantna u smjeru minimalnog faktora lokalnog mjerila duljina.

(1,3)

Ako je u nekoj točki a = b = 1, možemo reći da je u toj točki distorzija jednaka nuli ili da je to standardna točka.

(2,1)

Ako je u svim točkama neke linije a = 1, tada to općenito nije linija s distorzijom jednakom nuli, no možemo reći da je ta linija ekvidistantna u smjeru maksimalnog faktora lokalnog mjerila duljina.

(2,2)

Ako je u svim točkama neke linije b = 1, tada to općenito nije linija s distorzijom jednakom nuli, no možemo reći da je ta linija ekvidistantna u smjeru minimalnog faktora mjerila duljina.

(2,3)

Ako je u svim točkama neke linije a = b = 1, tada je to linija s distorzijom jednakom nuli, odnosno standardna linija.

(3,1)

Ako je u svim točkama nekog područja a = 1, tada možemo reći da je to područje preslikano ekvidistantno u smjeru maksimalnog faktora lokalnog mjerila duljina.

(3,2)

Ako je u svim točkama nekog područja b = 1, tada možemo reći da je to područje preslikano ekvidistantno u smjeru minimalnog faktora lokalnog mjerila duljina.

(3,3)

Izraz a = b = 1 ne može biti istinit u svim točkama nekog dvodimenzionalnog područja na karti, jer bi to značilo da je kartografska projekcija bez distorzija. Leonhard Euler prvi je dokazao da je to nemoguće (Euler 1777).

U posebnom slučaju kad je F = 0 možemo se koristiti s h i k umjesto a i b.

Ako je za sve točke nekog meridijana h = 1, to općenito nije meridijan s distorzijom jednakom nuli, nego meridijan uzduž kojega ili u smjeru kojega je distorzija jednaka nuli. Možemo reći da je meridijan preslikan ekvidistantno.

Ako je u svim točkama preslikanog područja h = 1, tada kažemo da je kartografska projekcija ekvidistantna uzduž meridijana. Na primjer, Postelova projekcija je azimutna projekcija ekvidistantna uzduž meridijana.

Ako je u svim točkama neke paralele k = 1, to općenito nije paralela s distorzijom jednakom nuli, nego paralela uzduž koje ili u smjeru koje je distorzija jednaka nuli, Možemo reći da je paralela preslikana ekvidistantno.

Ako je za sve točke nekog područja k = 1, tada kažemo da je kartografska projekcija ekvidistantna uzduž paralela. Na primjer, uspravna ortografska projekcija je ekvidistantna uzduž paralela.

Ako u svim točkama nekog meridijana vrijedi h = k = 1, to je meridijan s distorzijom jednakom nuli u svim smjerovima, tj. to je standardni meridijan.

Ako u svim točkama neke paralele vrijedi h = k = 1, to je paralela s distorzijom jednakom nuli u svim smjerovima, tj. to je standardna paralela.

4. Ekvidistantne, standardne i presječne paralele

Uspravni aspekt cilindričnih projekcija sfere su preslikavanja definirana formulama

x = R_n(λ-λ)₀, y = Rf(φ), (8)

gdje

, λ ∊ [-π ,π], konstante su n>0, R>0 i λ₀ ∊ [-π ,π], funkcija y = Rf(φ) je neprekidna, diferencijabilna, monotono rastuća i neparna. Kao kod svake kartografske projekcije x i y su koordinate točke u pravokutnom (matematičkom, desno orijentiranom) koordinatnom sustavu u ravnini. Svatko može vidjeti da je riječ o preslikavanju u ravninu, a ne na plohu cilindra. Za takvo preslikavanje imamo

i prva diferencijalna forma glasi

Kvadrat faktora lokalnog mjerila duljina za preslikavanje sfere radijusa R pri uspravnom aspektu cilindrične projekcije (8) je

Faktori lokalnog mjerila duljina uzduž meridijana, odnosno paralele su

Za uspravni aspekt cilindrični projekcija uzduž standardnih paralela kojima odgovaraju geografske širine φ±φ₁ mora biti

φ±φ₁ it should be h(φ₁) = k(φ₁) = 1, (13)

Ili uzevši u obzir (12) i (9)

i

Iz formule (15) i svojstava trigonometrijske funkcije kosinus možemo zaključiti da ako je geografska širina standardne paralele φ ₁, tada to mora biti i -φ ₁. O broju standardnih paralela pri uspravnom aspektu cilindričnih projekcija možemo zaključivati na temelju relacija (14) i (15).

Ako je 0<n<1 tada postoje dvije standardne paralele (φ₁ i -φ₁), ako je

Ako je n = 1 tada postoji jedna standardna paralela (φ₁ = 0), ekvator, ako je

Ako je n>1 tada ne postoji φ₁ za koji bi vrijedilo (15), tj. ne postoji ni jedna standardna paralela.

Neka su φ i -φ geografske širine dviju paralela preslikanih u uspravnom aspektu cilindrične projekcije (8). Vertikalna udaljenost između tih dviju paralela na sferi j2 Rsinφ, a udaljenost između njihovih slika u ravnini projekcije (vidisliku 2) je 2y( φ). Jasno je da 2 y( φ) = 2Rsinφ, tj. y( φ) = Rsin φ općenito nije istina. To vrijedi samo za Lambertovu ekvivalentnu projekciju. Dakle, savijanje karte izrađene u uspravnoj cilindričnoj projekciji u cilindričnu plohu i zatim stavljanje te plohe u poseban položaj prema sferi općenito nema smisla. Drugim riječima, kartografska projekcija i savijanje ili razvijanje cilindrične plohe su dvije potpuno različite aktivnosti. Budući da presječne paralele nemaju nikakvo posebno svojstvo u smislu razdiobe distorzije, zaključujemo da upotreba cilindričnih ploha u teoriji kartografskih projekcija općenito nema smisla i može dovesti do pogrešnih zaključaka o identičnosti presječnih i standardnih paralela (slika 3). Upotreba cilindričnih ploha ima smisla samo kod perspektivnih projekcija na cilindar, no takve projekcije se rijetko primijenjuju.

Zaključimo o cilindričnim projekcijama zadanima s (8):

Dvije paralele (φ₁ i -φ₁) su ekvidistantne paralele ako je

n = cosφ ₁ (16)

Dvije paralele (φ₁ i -φ₁) su standardne paralele ako vrijedi (16) i

Dvije (φ₁ i -φ₁) su presječne paralele ako je udaljenost između tih dviju paralela na sferi jednaka udaljenosti između njihovih slika u ravnini projekcije:

f (φ₁) = sinφ₁. (18)

Slijede dva primjera o cilindričnim projekcijama.

Neka je uspravni aspekt cilindrične projekcije definiran ovako

, λ ∊ [-π ,π], gdje su konstante R>0 i λ₀ ∊ [-π ,π]..

Budući da je f(φ) = φ i

možemo zaključiti da su u toj projekciji svi meridijani preslikani ekvidistantno (h = 1). Iz uvjeta

, koji se lako može izvesti iz (15) i (19), vidimo da se paralele koje odgovaraju geografskim širinama

također preslikavaju ekvidistantno

Budući da se svi meridijani u toj projekciji preslikavanju ekvidistantno, dvije ekvidistantno preslikane paralele su standarnde paralele

Udaljenost između dviju paralela koje odgovaraju geografskim širinama latitudes φ i -φ na sferi je 2 Rsin φ (vidisliku 2). Ako je

tada je udaljenost između tih dviju paralela na sferi jednaka

Udaljenost između njihovih slika u ravnini projekcije je 2y(φ) = 2R(φ), što za

iznosi

Dakle, savijanjem karte u cilindričnu plohu i postavljanje cilindra tako da se njegova os poklopi s pravcem koji spaja sjeverni i južni pol, i postavljanjem slike ekvatora u ekvatorijalnu ravninu, nije moguće da se presječne paralele podudaraju s ekvidistantnima (u ovom slučaju također standardnim paralelama). Dakle, pokazali smo da presječne i standardne paralele u cilindričnim projekcijama općenito nisu identične.

Jednadžbe Behrmannove projekcije glase (Lapaine 2018)

Za tu projekciju imamo

i odatle

Odmah se vidi da je ta projekcija ekvivalentna jer vrijedi hk = 1 za svaki φ.

Snyder i Voxland (1989) pišu da je Behrmannova projekcija istinita uzduž geografske širine 30° i da je to projekcija na presječni cilindar pri ±30° (True along latitudes ±30°, projection onto a cylinder secant at ±30° ). Standardne paralele Behrmannove projekcije odgovaraju geografskim širinama ±30°. Udaljenost izmeđuj tih paralela na sferi polumjera R je očito R. U ravnini Behrmannove projekcije udaljenost između njihovih slika je

što je očito različito od R. To znači da karta ne može biti izrađena u Behrmannovoj projekciji razvijanjem u ravninu Behrmannove cilindrične plohe koja siječe sferu uzduž paralela koje odgovaraju geografskim širinama ±30°. Obratno, karta izrađena u Behrmannovoj projekciji ne može se saviti u cilindričnu plohu koja će siječi sferu uzduž paralela kojima odgovaraju geografske širine ±30°. Identificiranje ekvidistantnih ili standardnih paralela s paralelama u kojima cilindrična ploha siječe Zemljinu sferu očito nije dobar postupak (Lapaine 2018).

Konusna projekcija je preslikavanje definirano formulama

ρ = Rf(φ), θ = n(λ-λ₀) (23)

gdje je

, λ ∊ [-π ,π], konstante su n>0, R>₀ i λ₀ ∊ [-π ,π], a funkcija ρ = Rf(φ) je neprekidna, s pozitivnim vrijednostima i monotono padajuća ili monotono rastuća, ρ i θ su koordinate točke u polarnom koordinatnom sustav u ravnini projekcije. Kao što se može vidjeti riječ je o preslikavanju u ravninu, a ne na konusnu plohu. Za takvo preslikavanje vrijedi

a prva diferencijalna forma ima oblik

Kvadrat faktora lokalnog mjerila duljina za uspravni aspekt konusne projekcije (23) je

Iz (26) možemo pročitati faktore lokalnih mjerila duljina uzduž meridijana, odnosno paralela,

Predznak minus u formuli za h odabran je stoga što su po pretpostavci funkcije ρ i f monotono padajuće. Kad bi te funkcije bile monotono rastuće, tada bi trebalo φ zamijeniti s -φ u izvodima koji slijede.

Kod uspravnog aspekta konusnih projekcija F = 0 i vrijedi (27).

Ako za svaki

vrijedi

tada se svi meridijani preslikavaju ekvidistantno. Ako je za neki

,

tada se paralele kojima odgovaraju te geografske širine preslikavaju ekvidistantno.

Uzduž standardne paralele φ = φ ₁ treba vrijediti

h(φ ₁) = k(φ ₁) = 1, (28)

to jest,

i

Ne možemo donijeti nikakav zaključak o broju standardnih paralela u uspravnom aspektu konusnih projekcija kao što smo mogli kod cilindričnih. Naime, za zadani n postoji beskonačno mnogo neprekidnih funkcija ρ = Rf(φ), koje su diferencijabilne s pozitivnim vrijednostima i monotono padajuće za

, i koje zadovoljavaju uvjete (29) i (30) za nekoliko razlićitih vrijednosti geografskih širina

Uočimo dvije paralele na sferi radijusa R, i neka su φ’ i φ’’ odgovarajuće geografske širine 0 ≤ φ’<φ’’ ≤ 90° . Najkraća udaljenost d između tih dviju paralela (slika 4) jednaka je

Udaljenost između njihovih slika na karti bit će

Međutim, jednakost

općenito ne vrijedi. Dakle, to nije primijenjivo na paralele preslikane ekvidistantno ili na stardardne paralele. To znači da savijanje karte izrađene u uspravnom aspektu konusne projekcije u konusnu plohu i njezino postavljanje u posebna položaj u odnosu na sferu općenito nema smisla. Drugim riječima, kartografska projekcija i razvijanje konusne plohe u ravninu su dvije različite aktivnosti. Budući da presječne paralele nemaju neko posebno svojstvo s obzirom na raspodjelu distorzije, zaključujemo da upotreba konusnih ploha u teoriji kartografskih projekcija općenito nema smisla i može voditi na pogrešne zaključke o identičnosti presječnih i standardnih paralela.

Zaključno o svojstvima konusnih projekcija zadanih s (23) i dvije paralele (0 ≤ φ' < φ" ≤ π/2):

Dvije paralele (φ’ and φ’’) su ekvidistantne paralele ako je

nf(φ') = cos φ' and nf(φ'') = cos φ''. (34)

Dvije paralele (φ’ and φ’’) su standardne paralele ako vrijedi (34) i

df/dφ (φ') = 1 and df/dφ (φ'') = 1 (35)

Dvije paralele (φ’ and φ’’) su presječne paralele ako je udaljenost između tih dviju paralela na sferi jednaka udaljenosti između njihovih slika u ravnini projekcije:

f(φ')-f(φ") = 2sin sin(φ"-φ')/2 (36)

Three examples on conical projections follow.

4.2.1. Example 3

Let the normal aspect conical projection be defined as:

gdje je

λ ∊ [-π ,π], R>0 and λ₀ ∊ [-π ,π]. Budući da je

i

zaključujemo da su svi meridijani preslikani ekvidistantno.

Uvjet (34) implicira da su i dvije paralele kojima odgovaraju geografske širine 0 ° i 60 ° preslikane ekvidistantno

Budući da su svi meridijani u toj projekciji preslikani ekvidistantno (h(φ) = 1 za sve φ), dvije ekvidistantno preslikane paralele su standardne paralele.

Udaljenost d između dviju paralela s geografskim širinama φ’ i φ’’ na sferi dana je formulom (36). Ako je φ’ = 0° and φ’’ = 60°, tada je udaljenost između tih paralela na sferi jednaka 2Rsin30° = R. Udaljenost između njihovih slika u ravnini projekcije je

, a za φ' = 0° and φ'' = 60° to je

što je različito od R. Dakle, savijanjem karte u konusnu plohu i postavljanjem te plohe tako da joj se os poklapa s pravcem koji spaja sjeverni i južni pol, nije moguće dobiti presječne paralele identične standardnim paralelama. Prema tome, pokazali smo da presječne i standardne paralele u konusnim projekcijama općenito nisu identične.

U vrlo poznatoj knjizi o kartografskim projekcijamaRichardus i Adler (1972, str. 94) interpretirali su Lambertovu konformnu konusnu projekciju s dvije standardne paralele i ilustrirali izvod crtežom konusa koji siječe elipsoid u dvije paralele (slika 5). Richardus i Adler željeli su pokazati da su te paralele istodobno presječne i standardne, no to ne može biti istina ako prihvatimo definiciju presječnih i standardnih paralela preporučenu u ovom članku. Dokažimo to na jednostavnom primjeru sfere radijusa 1 i Lambertove konformne konusne projekcija s dvije standardne paralele kojima odgovaraju geografske širine φ’ = 0° and φ’’ = 60°.

Najprije uočimo da nema posredne konusne plohe u Lambertovoj konformnoj konusnoj projekciji. To se vidi i iz Lambertova izvornog tekst ili prijevoda na engleski (Lambert 1772).

Ako karta u Lambertovoj konusnoj konformnoj projekciji ima dvije standardne paralele (desni dioslike 5), onda je nije moguće saviti u konusnu plohu koja bi sjekla Zemljinu sferu uzduž tih dviju paralela (lijevi dioslike 5), Premda to nekoga može iznenaditi, dokazat će se u ovom primjeru.

Da bi konusna projekcija bila konformna, mora vrijediti

h = k, (38)

gdje su h i k definirani u (27). Odatle, jer je R =1, slijedi

i zatim

odakle nakon integracije dobijemo

tj.

gdje je C konstanta integracije.

Neka su φ₁ = 0° and φ₂ = 60°dvije standardne paralele. Uvjeti za standardne paralele

i

čine sustav od dvije jednadžbe s dvije nepoznanice, n i C, koji se može transformirati u

i

odakle slijedi

i

Ako uvrstimo φ₁= 0° and φ₂= 60° dobit ćemo

Udaljenost između slika standardnih paralela s geografskim širinama φ₁= 0° and φ₂= 60° u ravnini Lambertove konformne konusne projekcije jednaka je

koji spaja sjeverni i južni pol na sferi. Nije moguće postići da se presječne paralele poklope sa standardnim paralelama jer je najkraća udaljenost između standardnih paralela na sferi mjerena uzduž pravca koji ih spaja jednaka 1 (slika 6). Savijanje (ili razvijanje) je izometrija, tj. transformacija koja čuva udaljenosti.

Ako savijemo kartu izrađenu u uspravnom aspektu konusne projekcije i pokušamo je postaviti u poseban položaj u odnosu na sferu, standardne paralele u toj projekciji neće se poklopiti sa standardnim paralelama na sferi. Drugim riječima, kartografska projekcija i savijanje ili razvijanje konusne plohe dvije su potpuno različite aktivnosti.

Dokazali smo da presječne paralele općenito nisu standardne paralele.

Snyder (1993) u svojoj čuvenoj knjizi Flattening the Earth, kaže na str. 123, "Kao i kod centralne ciloindrične projekcije opisane prije, konusna projekcija može se razviti geometrijskim projiciranjem globusa iz njegova središta na konus koji je tangencijalan u jednoj paraleli ili siječe u dvije. To je toliko elementarno da izgleda da nema formalnog izvora za to ...". Citiramo dalj: "Za dvije standardne paralele φ ₁ and φ ₂, polarne koordinate su kako slijedi:

, θ = λsin(φ₀),

gdje je

... Za tangencijalni slučaj s jednom standardnom paralelom, φ₁ se može izjednačiti s φ₂ Ako su standardne paralele na sjevernoj hemisferi, normalno se može prikazati samo dio južne hemisphere". Snyder je očito bio uvjeren da postoji gnomonska ili centralna perspektivna projekcija na konus s dvije standardne paralele. On to nije provjeravao, nego prihvatio kao činjenicu, premda pogrešnu. Evo dokaza!

Faktor lokalnog mjerila duljina uzduž meridijana u uspravnom aspektu konusne projekcije određen je prema (27)

Za funkciju ρ = ρ(φ) definiranu s (49) može se lako izračunati

i zatim

odakle je

što je različito od 1, osim ako je φ₁ = φ₂. Pokazali smo da jednostavna gnomonska perspektivna projekcija na konusnu plohu ne može imati dvije standardne paralele. Drugim riječima, ako konusna ploha siječe sferu uzduž dviju paralela te dvije paralele ne mogu biti standardne paralele gnomonske perspektivne projekcije.

5. Zaključak

Zaključujemo da objašnjavanje cilindričnih i konusnih projekcija kao projekcija na cilindričnu ili konusnu plohu nije dobar pristup, jer vodi na pogrešno razumijevanje nekih svojstava projekcije. Nadalje, standardne i presječne paralele često se smatraju identičnima, no u ovom se članku pokazuje da su naširoko prihvaćene činjenice o presječnim i standardnim paralelama (koje se mogu naći u literaturi) pogrešne i moraju biti revidirane. To zahtijeva kritički pristup prema ustanovljenim običajima u poučavanju i istraživanju kartografskih projekcija. U nekoliko prethodno objavljenih članaka pokazano je da postoje konusne i azimutne projekcije s tri i više standardnih paralela. Očito je da se to ne može interpretirati s pomoću presječnih projekcija i vodi na razlikovanje standardnih i presječnih paralela. Ekvidistantne projekcije su poznate u teoriji kartografskih projekcija. Ovaj članak uvodi ekvidistantnost u širem smislu. Ekvidistantnost se definira u točki, uzduž linije i na području. To omogućava definiranje triju tipova paralela: presječne, standardne i ekvidistantne. Dani su eksplicitni uvjeti za ekvidistantne, standardne i presječne paralele za cilindrične i konusne projekcije. Teorijska razmatranja ilustrirana su odgovarajućim primjerima.

Da bi se spriječilo pogrešno razumijevanje u teoriji kartografskih projekcija i njihovu poučavanju preporučamo izbjegavanje upotrebe razvojnih ploha kao posrednih ploha i razlikovanje ekvidistantnih, standardnih i presječnih linija.