1. UVOD
Međusobni odnosi figura u šahovskoj partiji mogu se prikazati evoluirajućim kompleksnim mrežama (evolucija grafa u ovom kontekstu podrazumijeva promjenu strukture grafa, odnosno, rast mreže reflektiran u svakom sljedećem potezu) koje opisuju taktičke i strateške elemente šahovske igre (Farren et al., 2013) . Mreže sadrže vrijedne informacije o partiji, o njezinim prijelomnim trenucima te ishodu, čak i kada šahovsku partiju prikažemo kao mrežu međusobnih odnosa figura, izostavljajući ostale pojedinosti o partiji, poput vrijednosti figura ili važnih strateških koncepata, poput šahovskog centra. Prikazavši partiju kao niz mreža, od kojih svaka modelira određeni aspekt veza između figura i ploče, moguće je prikupiti još takvih informacija. Nadalje, razmotri li se i evolucija grafova, odnosno, mreža u vremenskome tijeku koji odgovara tijeku partije, konačan model može se proširiti i vremenskom informacijom. Pomoću niza evoluirajućih mreža, odnosno, informacija izlučenih iz mreža rastućih kroz vrijeme , samo s minimalnom reprezentacijom pravila i logike same šahovske igre moguće je generirati vjerodostojnu evaluaciju svake pozicije u igri (Jokić, 2014 ; Jokić, 2018) .
U ovom se radu razmatraju informacije koje mogu biti dobivene iz konstruiranih mreža, tj. kumulativni mrežni podaci dobiveni iz evolucije mreža igre te se pokazuje kako one mogu uspješnije predvidjeti ishod partije od Shannonove klasične evaluacijske funkcije (Shannon, 1988) . Evaluacijska je funkcija složena formula, svojevrsni agregirani kvantifikator procjene igre, koji kvantificira sve značajke u proizvoljnoj poziciji i dodjeljuje im težine koje reflektiraju kako taktičke, tako i strateške kvalitete pozicije (Chessprogramming, 2018) . Stratešku kvalitetu pozicije zahtjevno je matematički modelirati pa, iako su moderni šahovski programi davno nadmašili najbolje svjetske igrače u toj sposobnosti procjene, to još uvijek predstavlja zahtjevan problem ( Atkin i Witten, 1975 ; Fernández i Salmerón, 2007 ; Farren et al., 2013 ; Lei, 2015 ; Silver et al., 2017 ; Jokić, 2018) . Razmatrajući pokazana svojstva takvih šahovskih programa i sustava, poput današnjih najboljih šahovskih paketa (engl. engines) Stockfish (Stockfish 10, 2018) i Komodo (Komodo 12, 2018) , neizbježno se nameće zaključak kako postoji malo mogućnosti i prostora za poboljšanjem rada takvih programa, s posebnim naglaskom na modernoj evaluacijskoj funkciji (Fernández, 2008) .
U ovom se radu upotrebljavaju principi strojnog učenja ( James et al., 2013 ; Stuart et al., 2015 , Silver et al., 2017) koji se često primjenjuju i pri predviđanju ishoda šahovske igre (Fernández, 2007) ili igre Go (Stern et al., 2006) . Nadalje, značajke, odnosno, vektori značajki koji se koriste u postupcima učenja šume slučajnih stabala (Breiman, 2001) temelje se na mjerama kompleksnih mreža (Newman, 2018) . Kompleksne mreže primjenjuju se na raznim područjima, poput predviđanja novih veza u društvenim mrežama (Martinčić-Ipšić et al., 2017) , određivanja ključnih riječi u tekstu ( Beliga et al., 2015 ; Beliga et al., 2016 ), modeliranja jezika (Martinčić-Ipšić et al., 2016) , analize koautorstva (Meštrović i Grubiša, 2015) i sličnog, dok je šahovska igra samo mjestimično modelirana kroz formalizme kompleksnih mreža, i to u radu (Farren et al., 2013) , stoga je to upravo i predmet istraživanja.
U radu se istražuju mogućnosti modeliranja šahovske igre kroz formalizam kompleksnih mreža, s ciljem dobivanja boljeg uvida u razvoj šahovske partije, te uvida u način na koji informacije dobivene iz strukture kompleksnih mreža utječu na predviđanje konačnog ishoda partije. U radu su navedeni različiti načini prikaza šahovske partije u formalizmu kompleksne mreže te su opisane značajke koje je moguće dobiti analizom strukture mreža. Nakon toga, svojstva mreže, kvantificirana u mjerama mreže, upotrebljavaju se za predviđanje ishoda partije izgradnjom klasifikatora. Klasifikacijski model gradi se pomoću algoritma strojnog učenja – šume slučajnih stabala - koji je po prvi puta primijenjen na problem predviđanja ishoda šahovske igre na temelju značajki dobivenih iz strukture kompleksne mreže. U radu se također pokazuje kako je moguće odrediti skup značajki koji najbolje pridonosi točnosti modela klasifikacije pozicija, odnosno, predviđanja ishoda igre.
2. METODOLOGIJA ISTRAŽIVANJA
2.1 Shannonova evaluacijska funkcija
Šahovska se igra proučava s puno različitih polaznih gledišta. Tako je, u domeni računalne znanosti, Claude Shannon, 50-ih godina 20. stoljeća, u svom teorijskom postulatu o mogućem radu šahovskih programa (Shannon, 1988) , naveo donju granicu kompleksnosti stabla igre, odnosno, prostora stanja šaha, te evaluacijsku funkciju oblika:
f(K,Q,R,B,N,P,DP,BP,IP,M)= 200(K − K') + 9(Q − Q') + 5(R − R') + 3(B − B' + N − N') + (P − P')− 0.5(DP − DP' + BP − BP' + IP − IP') + 0.1(M − M'), (2.1)
pri čemu su:
K, Q, R, B, N, P oznake za broj bijelih figura: K - kralja, Q - dame, R - topova, B - lovaca, N - skakača i P – pješaka,
DP, BP, IP oznake za broj DP - udvostručenih, BP - zaostalih i IP - izoliranih bijelih pješaka
M oznaka predstavlja faktor mobilnosti bijelog igrača (mjerenih npr. brojem mogućih legalnih poteza koje ima na raspolaganju u danoj poziciji),
negirane oznake (') predstavljaju analogne vrijednosti navedenih mjera za crnog igrača.
Iako su moderne evaluacijske funkcije značajno unaprijeđene od izvorne Shannonove evaluacijske funkcije, u ovome je radu upravo taj model primijenjen na osnovu s kojom se uspoređuje uspješnost predloženog rješenja. Razlog tomu je, ponajprije, jednostavnost strojne implementacije Shannonove evaluacijske funkcije te činjenica da moderni šahovski programi upotrebljavaju iznimno složene formule za evaluaciju statičkih pozicija (npr. dubinske neuronske mreže), koje je teško interpretirati. Nadalje, evaluacijske funkcije koje je moguće interpretirati najčešće predstavljaju linearnu kombinaciju nezavisnih značajki i njihovih pripadnih vrijednosti, poput Shannonove funkcije upotrijebljene u ovome radu, stoga je za usporedbu rezultata odabrana osnovna, ali jednostavno primjenjiva evaluacijska funkcija.
2.2 Kompleksne mreže
2.2.1 Potporna mreža (engl. support network)
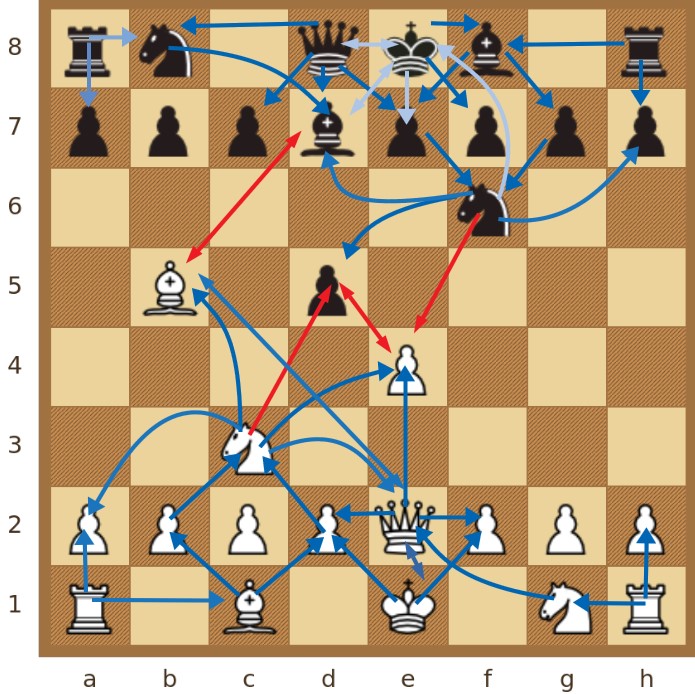
Prva vrsta kompleksne mreže koja se konstruira iz informacija o partiji takozvana je potporna mreža, koja modelira isključivo odnose između figura na ploči. U potpornoj mreži svaki čvor predstavlja figuru i iste je boje kao figura koju predstavlja. Kad figura ima potencijal uzimanja protivničke figure, taj je potencijal u potpornoj mreži prikazan vezom. U slučaju da figura napada figuru iste boje (što zapravo nije predviđeno pravilima igre), taj isključivo teorijski potencijal uzimanja vlastite figure također je moguće prikazati vezom. Sve su veze usmjerene i obojene s obzirom na boju figure koju predstavlja početni čvor veze. Nadalje, svakom je čvoru dodijeljen atribut koji predstavlja tip potencijala napada s vrijednostima u skupu ('napad', 'obrana'). Napadačke su veze između čvorova različite boje, dok su obrambene veze, analogno tome, veze između čvorova iste boje. Primjer takve mreže, s opisanim svojstvima, ilustriran je na Slici 1, koja sadrži proizvoljno zadanu poziciju na ploči, neposredno iz otvaranja igre. Potencijali uzimanja protivničke figure prikazani su na Slici 1, i to crvenom linijom od ishodišne figure, koja završava s odredišnom strelicom na polju napadnute figure (npr. C3→D5). Analogno tome, obrambeni potencijal svake figure naznačen je strelicama plave boje s ishodištem u polju obrambene figure (npr. G7→F6) te odredištem strelice na polju vlastite branjene figure.
2.2.2 Mreža mobilnosti (engl. mobility network)
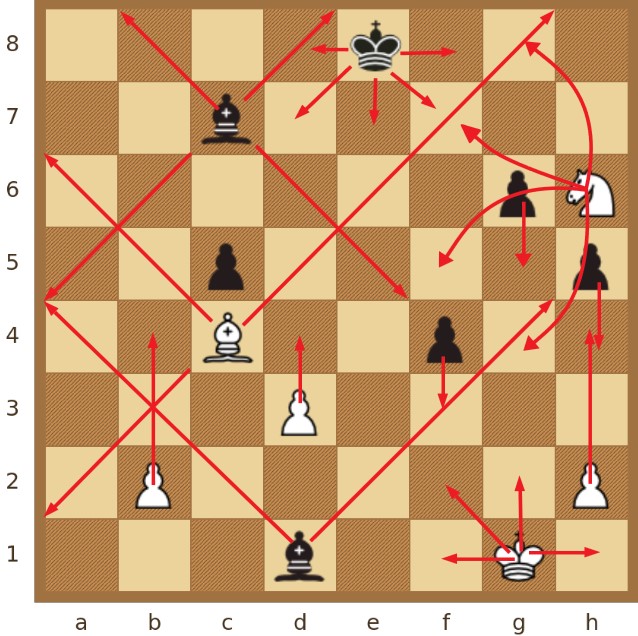
Druga je vrsta konstruirane kompleksne mreže tzv. mreža mobilnosti. Ona modelira mobilnost figura tako da je svaki čvor u mreži mobilnosti jedno polje na ploči. Polje može biti zauzeto nekom figurom ili izravno dostupno potezom neke figure. Svaki čvor koji predstavlja polje na kojem se nalazi figura preuzima boju figure koja ga okupira, tj. izvorišne figure. Mrežni čvorovi koji predstavljaju prazna polja nisu obojeni. Veze u mreži mobilnosti predstavljaju potencijal figure da uzme protivničku figuru ili se pomakne na dostupno prazno polje. Svaka je veza usmjerena i izvire iz čvora izvorišne figure. Odredište je svake veze čvor koji predstavlja bilo polje na kojem se nalazi figura napadnuta od strane izvorišne figure (isto kao i u potpornoj mreži), bilo prazno polje koje je dostupno izvorišnoj figuri veze. Ne postoje veze između čvorova koji predstavljaju polja okupirana figurama iste boje. Čvorovima koji predstavljaju prazna polja izlazni je stupanj vrijednosti nula, dakle nisu povezani. Svaka je veza obojena bojom izvorišnog čvora. Radi dosljednosti, svakoj je vezi dodijeljen atribut s vrijednošću 'napad'.
2.2.3 Pozicijska mreža (engl. position network)
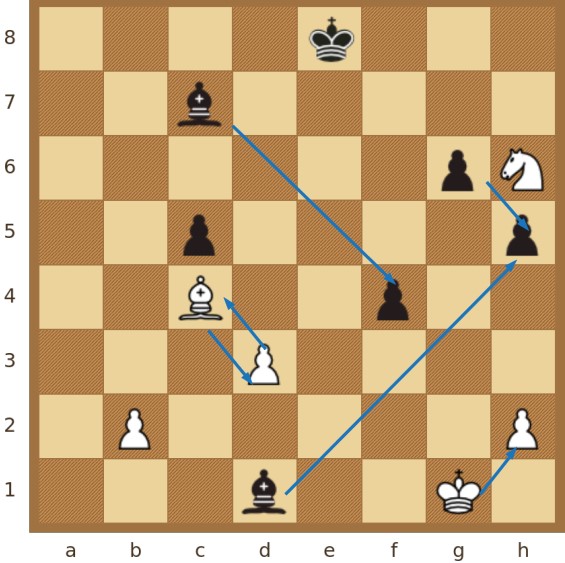
Treća je vrsta konstruirane kompleksne mreže tzv. pozicijska mreža - u osnovi spoj prethodnih dviju mreža - mreže mobilnosti i potporne mreže, a modelira odnose između figura i polja koja mogu doseći. Primjer pozicije na dijagramu na kojem su naznačene dodatne veze u pozicijskoj mreži, u odnosu na mrežu mobilnosti, prikazan je na Slici 3.
2.2.4 Mreža praćenja (engl. tracking network)
Četvrta je vrsta konstruirane kompleksne mreže tzv. mreža praćenja, koja modelira povijest kretanja figura kroz polja na šahovskoj ploči. To je tip mreže koji se upotrebljava za daljnje postupke izračuna, koji nije moguće dobiti iz statičke pozicije na ploči. U mreži praćenja svako je polje ploče predstavljeno čvorom. U tijeku igre, kada igrač na potezu pomakne figuru s izvorišnog na odredišno polje, taj se potez u mreži praćenja označava vezom od izvorišnog do odredišnog polja, odnosno, čvora mreže. Jednom kada se uspostavi veza, ona se ne briše do kraja partije. Svaki potez inkrementalno dodaje veze u mrežu, što znači da konačna mreža sadrži informacije, tj. povijest svih poteza odigranih u partiji, no ne i njihov vremenski slijed. Također, za figure dame, topa, lovca i pješaka, koji se mogu pomaknuti dalje od susjednog polja, stvaraju se dodatne veze za svako od prijeđenih prethodnih polja, počevši s izvorišnim poljem i prijeđenim poljem te završavajući s odredišnim poljem. Svaka veza u mreži obojena je kao i figura čije je kretanje rezultiralo stvaranjem te veze. Radi dosljednosti, svim je vezama dodijeljen atribut tipa 'napad'.
Na Slici 4, bijeli igrač odigrao je svoj prvi potez u partiji, potez kraljevim pješakom s polja E2 na polje E4. Tim prvim potezom, kao i svakim sljedećim potezom, nastaju nove veze iz izvorne mreže slijeda, koja je analogna početnoj poziciji u partiji prije prvog poteza. Tim prvim potezom, nastaju prve tri veze u mreži slijeda, a to su:
3. EMPIRIJSKI PODACI I ANALIZA
3.1 Upotrijebljene mrežne mjere u modelu
U radu se eksperimentalno analizira niz mrežnih svojstava, tj. mjera koje se upotrebljavaju za predviđanje krajnjeg ishoda partije. Upotrebljavaju se mrežne mjere u vektorima značajki, točnije, razlika njihovih vrijednosti za bijelu i crnu komponentu svake od mreža, i to za svaku od četiri konstruirane mreže pojedinačno. Upotrijebljene mjere kompleksne mreže definirane su standardno prema formulama u Jokić (2018) , Martinčić-Ipšić (2019) , Newman (2018) , stoga su ovdje samo navedene, bez definicije: najmanji stupanj čvora u mreži, najveći stupanj čvora u mreži, prosječni stupanj čvora, medijan distribucije stupnjeva čvorova, gustoća mreže/grafa, broj čvorova, broj veza i broj jako povezanih komponenti.
Iako mrežna svojstva, tj. mjere, modeliraju neke pozicijske i strateške aspekte igre, promatrana agregirano, količina je informacija o poziciji koje možemo dobiti iz jedne mreže mala te stoga nedostatna za zadovoljavajuću točnost predviđanja ishoda partije. Zbog toga će se navedene agregirane mrežne značajke (za svaku od četiri vrste opisanih mreža) kombinirati u jedan konačan vektor značajki s ukupno 33 vrijednosti, a koji će biti opisan u sljedećem poglavlju.
3.2 Učenje šume slučajnih stabala i određivanje vektora značajki
Klasifikacija u strojnom učenju ima zadatak razvrstati objekte u unaprijed definirane klase ili razrede. Kako bi se objekt mogao klasificirati, potrebno ga je vjerodostojno opisati podacima - značajkama (engl. features). Značajke se dobivaju pomoću različitih numeričkih izračuna nad izvornim podacima (James et al., 2013) . Primjer je jedne takve značajke srednja vrijednost intenziteta svjetline određene regije slike. Budući da jedna značajka ne može vjerodostojno predstavljati sve osobine modeliranog objekta, u većini se slučajeva izračunava veći broj značajki.
Nakon izračuna značajki i izgradnje vektora značajki za svaki potez u partiji, za svaku od partija iz baze majstorskih partija iz PGN (engl. Portable Game Notation) datoteka upotrebljava se algoritam strojnog učenja - šuma slučajnih stabala (engl. Random forest) (Breiman, 2001) . Algoritam iz raspoloživih podataka za učenje stvara veći broj (ansambl) (engl. ensamble) stabala odlučivanja - šumu slučajnih stabla. Pri konstrukciji svakog od stabala u šumi algoritam slučajnim odabirom uzima podskup podatkovnih instanci i podskup ulaznih varijabli. Prilikom izgradnje stabla, odluka o binarnoj podjeli podatka u čvoru donosi se prema funkciji koja određuje najbolju podjelu. Vremenska je kompleksnost tog algoritma procijenjena s O(MKN log2N), gdje je M broj stabala, N broj podatkovnih instanci, K broj varijabli. Uobičajeno se kao funkcija za određivanje grananja upotrebljava Gini indeks. Varijabla koja postigne najveću vrijednost Gini indeksa upotrebljava se za podjelu podataka u tekućem čvoru.
Gini indeks definiran je kao:
gdje je t trenutni čvor, pi vjerojatnost klase i u čvoru t, a m je broj klasa u modelu (u ovom je radu m=3).
Konačno predviđanje šume slučajnih stabala izračunava se kao prosjek predviđanja pojedinačnih stabala u šumi. Pokazano je da je taj model robustan i otporan na prekomjerno prilagođavanje podacima za učenje (engl. overfitting) te da postiže bolju točnost predviđanja od pojedinačnih stabala. Zbog svih dobrih svojstava, ovaj se algoritam često primjenjuje u različitim područjima istraživanja (Martinčić-Ipšić, 2019) . Nadalje, dobro je svojstvo tog algoritma i njegova sposobnost da odredi značaj varijabli (atributa). Ukoliko usporedimo pogrešku predviđanja kod stabla naučenog na cijelom skupu podataka za učenje s pogreškom predviđanja u stablu naučenom na podskupu podataka, koje smo slučajno permutirali tako da vrijednosti varijable (značajke) koju promatramo slučajno rasporedimo preko svih primjera u tom skupu, utvrdit ćemo utjecaj tj. važnost varijable. Veliko odstupanje pogreške predviđanja u tim dvama modelima ukazuje na važnost te varijable. To znači da slučajna permutacija vrijednosti značajno utječe na točnost predviđanja, što posljedično znači da je utjecaj te varijable na točnost predviđanja velik, dakle varijabla ima veliki značaj (engl. variable importance). Vrijedi i obrnuto: ukoliko je razlika u pogreškama mala, značaj varijable nije velik. U radu se upotrebljava MeanDecreaseGini - mjera značaja varijabli koja je zasnovana na Gini indeksu i koja se upotrebljava pri postupku određivanja važnosti varijabli (engl. variable importance). Testni skup partija različit je od skupa partija upotrebljavanih za učenje modela predviđanja - skupa za učenje (Stuart et al., 2005 ; Lai, 2015) . Dobiveni rezultati predviđanja uspoređuju se sa Shannonovom evaluacijskom funkcijom na testnom skupu partija.
Za izgradnju modela predviđanja upotrebljavaju se vektori značajki koji sadrže vrijednosti značajki za svaku od četiri opisane moguće vrste mreža upotrijebljenih za analizu, dakle, ukupno 32 vrijednosti (4x8), te za klasu (razred) koja je zapisana u 33. varijabli. Detaljan popis značajki nalazi se u privitku A ovoga rada, dok je ovdje naveden skraćeni oblik. Značajke V1-V8 redom odgovaraju najmanjem, najvećem i prosječnom stupnju čvora u potpornoj mreži, medijanu distribucije stupnjeva čvorova, gustoći, broju čvorova, broju veza i broju jako povezanih komponenti u potpornoj mreži. Značajke V9-V17 kvantificiraju osobine mreže mobilnosti, V18-V25 pozicijske mreže, dok značajke V26-V32 opisuju mrežu praćenja. Zadnja vrijednost, V33, predstavlja kategoričku varijablu odabira, tj. jednu od tri moguće vrijednosti {pobjeda crnog, remi, pobjeda bijelog}, od kojih svaka predstavlja predviđeni najvjerojatniji ishod partije iz dane pozicije, uzevši u obzir optimalnu igru oba igrača. To je klasa predviđena modelom, a može dobiti sljedeće vrijednosti:
-1 → pobjeda igrača s crnim figurama,
0.5 → remi-ishod,
1 → pobjeda igrača s bijelim figurama.
Dobivene evaluacijske vrijednosti preslikaju se u krajnju evaluacijsku mjeru na temelju raspona vrijednosti kojemu evaluacijska vrijednost pripada. Preslikavanje izračunanih evaluacijskih vrijednosti za svaku poziciju u skup od tri moguće vrijednosti dobiveno je distribuiranom analizom baze majstorskih partija pomoću šahovskog programa Stockfish, i to na sljedeći način: vrijednosti iz intervala [-MAX_VRIJEDNOST, - 0.51] pretvore se u vrijednost klase -1 - pobjeda crnog; vrijednosti iz [-0.5, + 0.5] u 0 – remi, te vrijednosti iz [0.51, +MAX_VRIJEDNOST] u 1 - pobjeda bijelog igrača.
Jedinice upotrebljavane u evaluacijskim vrijednostima šahovskih programa, poput Stockfisha takozvani su centi-pješaci, odnosno, 100-ti dio vrijednosti materijalne prednosti u vidu jednog pješaka više (100 centi-pješaka). S obzirom na trenutnu poziciju, nema konkretno definiranih granica, tj. raspona tako definiranih evaluacijskih vrijednosti koje 100% koreliraju s objektivnim krajnjim vjerojatnim ishodima partije, odnosno, evaluacijskom ocjenom dane statičke pozicije za oba igrača, dakako, pretpostavivši optimalnu igru oba igrača. Njemački je logičar i matematičar Ernst Zermelo 1913. godine objavio djelo u kojemu je dokazao da je optimalna strategija pri igranju šaha strogo određena (Zermelo, 1913) . Zbog kompleksnosti šahovske igre, nije uvijek vidljivo koje su to strategije, no dokazano je da postoje. U ovom kontekstu, pojam optimalno odnosi se na onakvu strategiju koja će igraču maksimalno pospješiti vjerojatnost pobjede, odnosno, umanjiti vjerojatnost poraza (min-max strategija).
3.3 Distribuirana obrada baze majstorskih partija
U radu se koristi ICOfy IB1421 PGN (engl. Portable Game Notation) baza koja sadrži sve partije za potrebe ove analize. Baza je filtrirana tako da uključuje odlučujuće partije s pobjedom jednog od igrača, bez remi-ishoda.Time se osigurava dovoljan broj pozicija za analizu u kojima jedan od igrača ima odlučujuću prednost nad protivnikom, s obzirom na to da je većina pozicija tijekom majstorskih partija u okviru remi-ishoda. Naime, odlučujuća se prednost u takvim partijama stječe tek u poodmakloj fazi partije. Filtriranjem remi-ishoda podatkovni se skup iz šahovske baze partija smanji na približno 62 200 partija. Važno je napomenuti da su na ovaj način preuzeti svi potezi iz filtriranih partija, koji su nazvani statičkim pozicijama. Za svaku statičku poziciju moguće je odrediti utječe li na pobjedu crnog, remi ili pobjedu bijelog igrača, što je opisano u nastavku.
Šahovska se baza dodatno predprocesira tako da se podijeli u PGN datoteke od kojih svaka sadrži 5000 partija. Naposljetku, u radu se upotrebljava samo prvih 5000 partija iz te baze, što se pokazalo dostatnim za eksperimente izvedene i opisane u nastavku rada.
Za obradu je napisana Python skripta koja distribuirano učitava svaku od partija u jednom od ukupno 2-4 konkurentna procesa, od kojih svaki izvršava svoju instancu Stockfish šahovskog programa (V8 u trenutku pisanja rada (Stockfish, 2018)) nad jednom partijom te analizira sve poteze partije. Skripta, odnosno, svaka pokrenuta instanca Stockfish programa izračunava svaki potez, tj. statičku poziciju nastalu na ploči kroz tijek partije te zapisuje u globalni rječnik ključ-vrijednost par koji sadrži numeričku evaluaciju pozicije. Globalni je rječnik Python rječnik koji dijeli svaki od zasebno pokrenutih procesa, a višeprocesni upravljač koordinira radom procesa i brine se o kontroli pristupa za dijeljeni resurs. Svaki par sastoji se od ključa koji predstavlja statičku poziciju pomoću Zobrist* hash-vrijednosti (Zobrist, 1969) , te njezinu Shannonovu evaluaciju. Time je izbjegnuto udvostručavanje izračuna evaluacije za već poznate pozicije, nauštrb veće varijacije u samom izračunu. No s obzirom na to da nije potrebna veća preciznost, tj. dubina pretrage za svaku poziciju, ovaj je pristup dostatan, posebice stoga što se navedene vrijednosti ne analiziraju numerički, već se pozicije klasificiraju u tri moguća skupa, odnosno, kategoričke vrijednosti koje predstavljaju tri moguća ishoda partije – pobjedu jednog od igrača te remi-ishod. Python skripte za distribuiranu obradu partija imaju linearnu vremensku složenost, tj. O(n).
4. REZULTATI KLASIFIKACIJE
4.1 Izgradnja šume slučajnih stabala i određivanje značaja varijabli
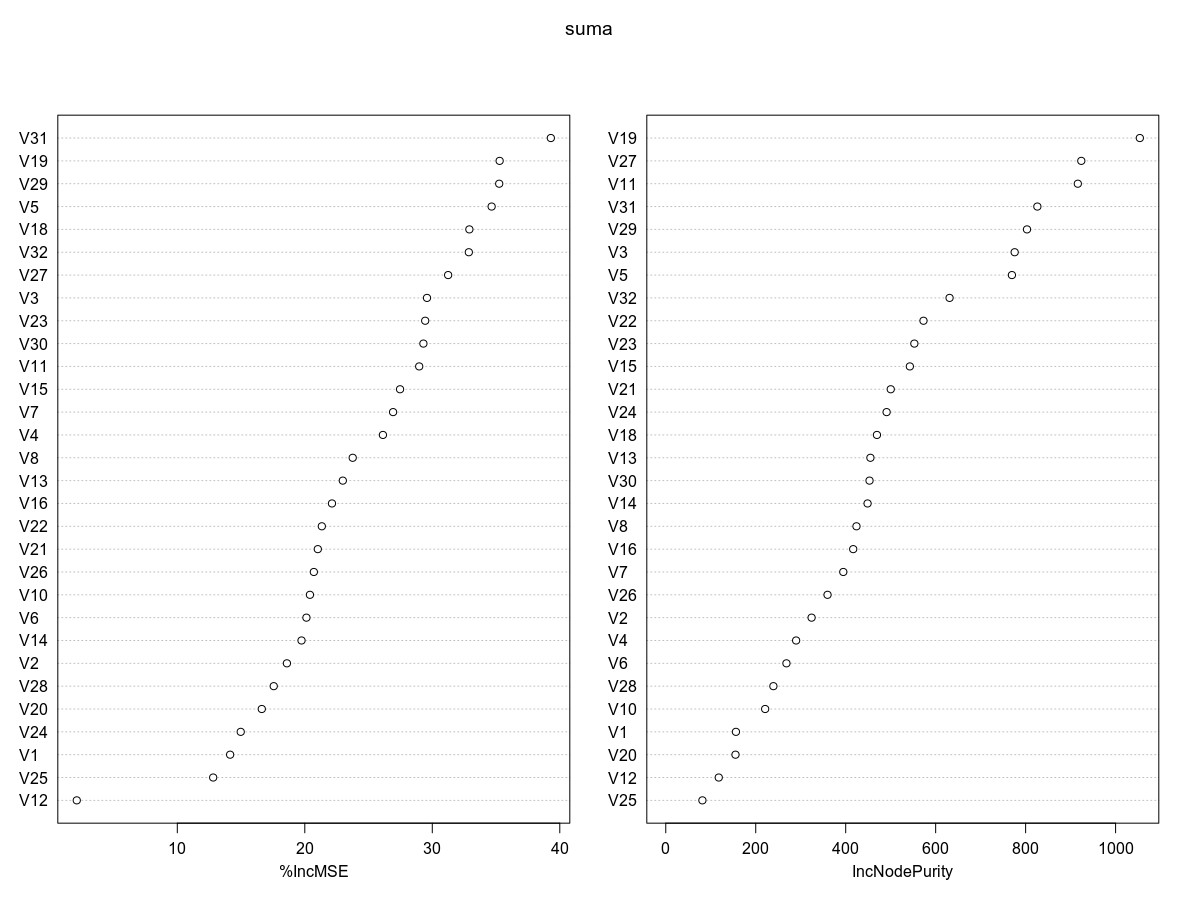
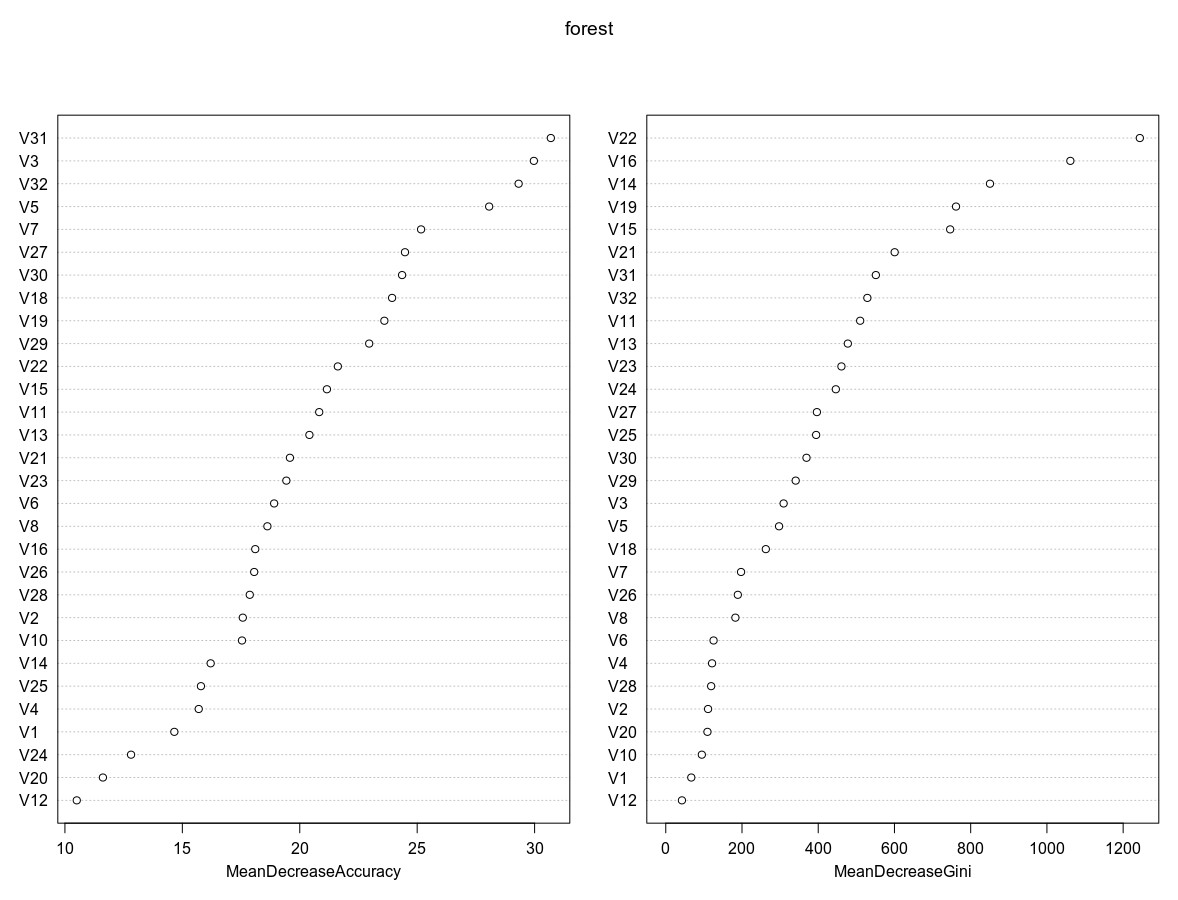
Nakon tvorbe konačnog skupa podataka za analizu, koji sadrži instance koje opisuju poteze, uči se model određivanja ishoda partije pomoću Random Forest (RF) biblioteke u R-programskom jeziku (Liaw, Wiener, 2018) , odnosno, alatu za statističku analizu podataka koji omogućuje provođenje postupaka linearne regresije i klasifikacije (James, 2013) . Prvi je korak pronalazak varijabli/mrežnih značajki koje više utječu na točnost predviđanja – klasifikacije poteza. U radu je pokazano i kako je moguća izgradnja manjeg klasifikacijskog modela na temelju smanjenog skupa značajki (visokorangiranih s obzirom na značaj), a koji nema smanjenu točnost predviđanja. Taj postupak opisuju rezultati na Slici 5, koja prikazuje dva grafa koja sadrže odabrane mrežne značajke u RF modelu (y–os), te dvije mjere na x-osi koje opisuju njihov utjecaj na porast, odnosno, pad točnosti u generiranom RF modelu (engl. variable importance). Dvije su mjere: %IncMSE (u lijevom dijelu) te IncNodePurity (u desnom dijelu slike). %IncMSE odražava porast MSE po varijabli (engl. mean-squared error), dakle odražava važnost varijable s obzirom na točnost predviđanja. IncNodePurity odražava gubitak koji proizlazi iz postupka odabira grananja na svakom koraku algoritma. Veći značaj varijabli (značajki) odgovara većoj vrijednosti %IncMSE i IncNodePurity vrijednosti s x-osi, i obrnuto, dakle, značajka V31 najviše je rangirana prema %IncMSE kriteriju, dok je značajka V19 najviše rangirana prema IncNodePurity kriteriju. Nadalje, iz slike je razvidno da je pet najviše rangiranih značajki V31, V19, V29, V5 i V18 prema %IncMSE kriteriju, odnosno, V19, V27, V11, V31 i V29 prema IncNodePurity kriteriju.
4.2 Rezultati predviđanja ishoda šahovskih partija
U nastavku su prikazani rezultati predviđanja ishoda šahovskih partija na temelju svih 32 značajki uključenih u učenje modela. Za evaluaciju se upotrebljava konfuzijska matrica i računa mjera točnosti (engl. accuracy - ACC). U konfuzijskoj je matrici za svaku od klasa napisan broj točnih (TP) i broj pogrešnih (TN) klasifikacijskih primjera. Mjera točnosti tada predstavlja omjer pravilno klasificiranih primjera (TP + TN) u odnosu na ukupan broj primjera:
gdje FP predstavlja broj lažno pozitivnih klasifikacijskih primjera, a FN broj lažno negativnih klasifikacijskih primjera. Budući da u ovome radu nema klasične binarne klasifikacije, već se radi s tri klase, za evaluaciju se upotrebljava prilagođena mjera točnosti. Računa se kao omjer broja točno klasificiranih primjera za danu klasu prema ukupnom broju stvarnih primjera za tu klasu. Uz to, radi se i s neuravnoteženim klasama (broj pojedinih primjera iz svake klase nije ujednačen: klasa -1 sadrži 9% primjera, klasa 0.5 73%, dok klasa 1 sadrži 18% primjera), za koje je primjerena mjera točnosti za klasu (engl. per-class accuracy). Rezultati evaluacije dobiveni su za sve značajke (ukupno 32) koje su upotrijebljene za izgradnju klasifikacijskog modela RF. Tablica 1 prikazuje matricu konfuzije koja sadrži rezultate klasifikacije na testnom skupu podataka.
| predviđene klase – ishodi partija | |||||
|---|---|---|---|---|---|
| stvarne klase - ishodi partija | -1 | 0.5 | 1 | pogreška klasifikacije | |
| -1 | 391 | 76 | 447 | 0.5722 | |
| 0.5 | 497 | 6281 | 582 | 0.1466 | |
| 1 | 710 | 229 | 893 | 0.5126 | |
Od svih uzoraka za testiranje (ukupno 914), u stablu koje pripada klasi -1 (pobjeda crnog), točno je klasificiran (predviđeno ishoda partije) 391 uzorak. Dakle, točnost klasifikacije za klasu -1 ACC-1 iznosi:
odnosno, 42.78%, čime pogreška klasifikacije iznosi 57.22%.
Na isti način računa se točnost, odnosno, pogreška klasifikacije za preostale dvije klase. Za klasu 0.5 (remi) točnost je PPV0.5:
odnosno, 85.34%, čime pogreška klasifikacije iznosi 14.66% te točnost klasifikacije PPV1 za klasu 1 (pobjeda bijelog) iznosi:
odnosno, 48.74%, čime pogreška klasifikacije iznosi 51.26%.
Analogno izračunu točnosti klasifikacije, za pojedinu se klasu izračunava i ukupna točnost klasifikatora izračunavanjem omjera zbroja svih točno klasificiranih uzoraka za sve klase naspram zbroja svih pogrešno klasificiranih uzoraka. Ukupna točnost klasifikacije ACC tada je:
odnosno, izračunana točnost iznosi 74.86% s pogreškom klasifikacije od 25.14%.
4.3 Značaj varijabli po Gini kriteriju
MeanDecreaseGinimjera je procjene važnosti atributa/varijable po Gini kriteriju, koji se uobičajeno upotrebljava za izračun grananja pri izgradnji klasifikacijskih stabala (James, 2013) . MeanDecreaseAccuracy mjera je procjene važnosti atributa/varijable koja se određuje prilikom faze izračuna OOB (engl. out-of-bag) klasifikacijske pogreške. Pri uzorkovanju nisu svi podaci uključeni u konačni skup za učenje – oni koji nisu, zovu se out-of-bag podaci i upotrebljavaju se pri procjeni pogreške generalizacije generiranog stabla, pa na kraju i čitave šume. Važnost varijable pozitivno je korelirana i s padom točnosti RF klasifikatora zbog izdvajanja (ili permutacije) jedne varijable, stoga su varijable s velikom MDA (engl. mean decrease accuracy) vrijednošću važnije za klasifikaciju.
U radu je odabrano prvih 10+ najvažnijih varijabli prema svakom od kriterija s obzirom na opisani kriterij prekida, i tako je dobivena formula za RF model, što je u R-u zapisano kao:
mdaFormula <- factor(V33) ~ V31+V3+V32+V5+V7+V27+V30+V18+V19+V29
giniFormula <- factor(V33) ~ V22+V16+V14+V19+V15+V21+V31+V32+V11+V13+V23+V24
4.4 Konačni evaluacijski model za smanjen broj varijabli po Gini kriteriju
Nakon određivanja varijabli koje imaju najveći utjecaj (značaj) na točnost klasifikacije, odnosno, najveću točnost predviđanja ishoda, izgradi se i sam model predviđanja – RF model – koji prilikom učenja gradi model klasifikacije samo za odabrane varijable, na sljedeći način:
formula <- factor(V33) ~ V3+V5+V29+V31+V11+V27+V19
forest_chop <- randomForest(formula, data=training_set)
forest_chop
Varijable za konačni RF model odabrane su na temelju grafa sa Slike 6 jer se usporedivi rezultati klasifikacije nad testnim skupom podataka dobivaju i s odabirom preostalih dviju navedenih formula (mdaFormula i giniFormula) ovdje nisu prikazane. Tablica 2 prikazuje matricu konfuzije sa smanjenim brojem varijabli za učenje.
| predviđene klase – ishodi partija | |||||
|---|---|---|---|---|---|
| stvarne klase – ishodi partija | -1 | 0.5 | 1 | pogreška klasifikacije | |
| -1 | 1788 | 1157 | 1847 | 0.626878 | |
| 0.5 | 436 | 18602 | 720 | 0.058507 | |
| 1 | 1514 | 1525 | 2727 | 0.527055 | |
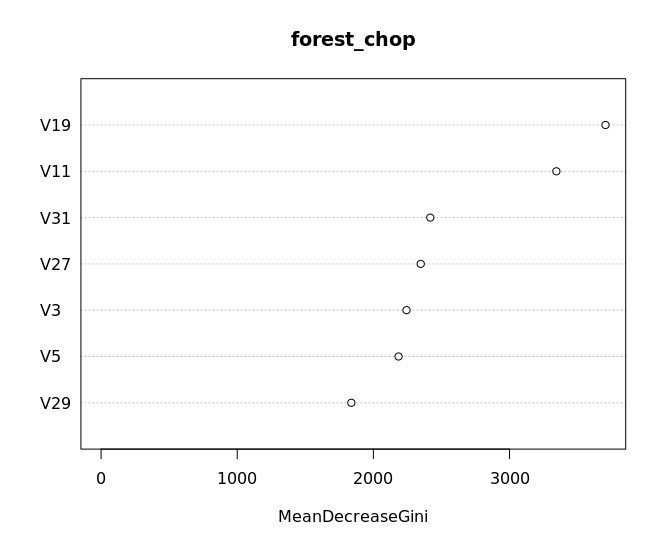
Na temelju rezultata na Slici 7, u daljnji se postupak uvode najviše rangirane značajke prema Mean decrease gini indexu - V19, V11, V31, V27, V3, V5 i V29.
pred <- predict(forest_chop, newdata = test_set) table(pred, test_set$V33)
Naposljetku, rezultati prikazani u Tablici 3 – konfuzijskoj matrici sa smanjenim brojem varijabli (7 – odabranih prema vrijednostima na slici 7) – za testni skup podataka pokazuju da je točnost klasifikacije ishoda novih šahovskih partija moguća s točnošću od 75.27%.
| predviđene klase – ishodi partija | |||||
|---|---|---|---|---|---|
| stvarne klase – ishodi partija | -1 | 0.5 | 1 | pogreška klasifikacije | |
| -1 | 557 | 171 | 495 | 0.544562 | |
| 0.5 | 418 | 6175 | 552 | 0.135759 | |
| 1 | 623 | 240 | 875 | 0.496547 | |
4.5 Usporedba rezultata predviđanja sa Shannonovom evaluacijom
Nakon izgradnje klasifikatora pozicija koji upotrebljava odabrane mrežne značajke, dakle one koje su se, empirijski gledano, pokazale najboljima po pitanju uspješnosti predviđanja, odnosno, evaluacije valjanosti pozicije, uspoređuje se točnost s klasičnom Shannonovom funkcijom. Rezultati točnosti predviđanja valjanosti svih pozicija iz skupa za testiranje moraju se dobiti i za Shannonovu evaluacijsku funkciju. To je postignuto s jednostavnom Python skriptom koja izračunava vrijednost Shannonove funkcije za sve pozicije iz testnog skupa pozicija te ih uspoređuje s već izračunanim evaluacijskim vrijednostima iz rječnika vrijednosti koji je izgrađen na temelju fiksne evaluacije Stockfish šahovskog programa svih pozicija iz testnog skupa partija. Od 145 846 analiziranih pozicijadobiveno je77 143 točnih, čime točnost Shannonove evaluacijske funkcije iznosi 52.89%.
Rezultat analize točnosti evaluacije svodi se na jednostavnu usporedbu točnosti naučenog modela RF sa Shannonovom evaluacijskom funkcijom za testni skup podataka prikazanima u Tablici 4.
| Točnost Shannonove evaluacijske funkcije | 52.89 % |
|---|---|
| Točnost RF modela | 75.27% |
| Točnost RF modela | 75.27% |
Na osnovi analize odabrane statičke pozicije na ploči razvidno je da Shannonova evaluacijska funkcija ima značajno lošiju točnost predviđanja ishoda trenutne partije, s obzirom na rezultate RF klasifikatora koji upotrebljava odabrane strukturne značajke mreže.
5. ZAKLJUČAK
U ovom je radu predstavljena mogućnost modeliranja šahovskih pozicija u šahovskim partijama nizom kompleksnih mreža, odnosno, izračunom mrežnih značajki. Kombiniranjem tih značajki i izgradnjom klasifikatora koji upotrebljava model šume slučajnih stabala postignuta je veća točnost predviđanja. Točnost klasifikatora nije samo dostatna za računalni šah, već i značajno nadmašuje točnost klasične Shannonove evaluacijske funkcije za čak 22.38%. Dobiveni rezultat nije iznenađujuć za šahovske igrače jer je poznato da suvremeni šahovski programi, koji su već odavno nadmašili najbolje ljudske igrače današnjice, imaju evaluacijske funkcije koje su nemjerljivo kompleksnije od jednostavnog predviđanja kvalitete pozicije koju odražava Shannonova evaluacijska funkcija. To, naravno, i nije čudno, s obzirom na to da je upravo Shannon udario čvrste temelje računalnom šahu sredinom prošlog stoljeća te se u praksi pokazalo da je njegov pristup računalnom šahu, utemeljen na Shannon A tipu računalnih šahovskih programa, još uvijek superioran u odnosu na programe koji nastoje oponašati ljudski način pristupa igri. Međutim, primjena takvog modela predviđanja, koji ne upotrebljava znanje o šahu niti pravila same igre, a daje obećavajuće rezultate, odaje dojam da će se u bližoj budućnosti pojaviti šahovski programi koji će nadmašiti postojeće ekstremno optimizirane klasične evaluacijske funkcije u modernim šahovskim programima. Neki od projekata koji danas upošljavaju duboke konvolutivne neuralne mreže, poput Google AlphaZero ( Silver, 2017 ; Alphazero, 2018 ) ili istraživanja opisanog u (Lei, 2015) , te projekta zajednice entuzijasta otvorenih tehnologija, Leela Chess Zero (Silver, 2018) , daju naslutiti da će se taj odnos uskoro promijeniti u korist potonjeg pristupa. Daljnja bi istraživanja kompleksnih svojstava i odnosa između evolucija šahovskih mrežnih modela i šahovskih strategija zbog toga mogla svakako biti vrlo plodonosna, s konkretnim praktičnim rezultatima. Nije isključena ni mogućnost primjene takvog pristupa pri daljnjem poboljšanju postojećih modernih šahovskih programa u vidu svojevrsnog hibridnog pristupa evaluaciji šahovskih pozicija i pronalaska optimalne strategije igre. Potrebno je naglasiti da glavna kritika svih dubokih neuralnih modela, unatoč postignutim visokim performansama na različitim područjima primjene, proizlazi iz njihove nerazumljivosti. Naime, neuronske mreže ponašaju se poput modela crne kutije, koji ne omogućava obrazloženje ponašanja, tj. objašnjenja dobivene evaluacijske vrijednosti u ovome slučaju, te stoga nisu primijenjene u ovome radu. Hibridni pristup pokušava razriješiti problem nerazumljivosti modela te će se u budućem radu posvetiti proučavanju hibridnog pristupa.