1. UVOD
Deformiranje metala objašnjava promjene u mikrostrukturi metala prilikom njegovog oblikovanja u konačan proizvod. Oblikovljivost se definira kao sposobnost materijala da se deformira određenim postupkom oblikovanja iz svog početnog oblika u zahtijevani oblik bez pojave greške. Duboko izvlačenje je tehnologija oblikovanja metala u hladnom stanju (iako se pojavljuje određena temperatura i nekim specifičnim slučajevima, može se obavljati i u toplom stanju) kod koje se pretvorbom iz ravne ploče u određeni geometrijski oblik izrađuju različiti proizvodi kao što su sudoperi, dijelovi automobila, kutije i slično. Riječ je, ukratko, o proizvodnji limenih proizvoda i preradi limova kod kojih postoji tendencija korištenja tanjih limova uz zadržavanje čvrstoće materijala, posebno u automobilskoj industriji. Manja masa automobila omogućava manju potrošnju energije za pokretanje automobila.
Vrlo je važno dobro odabrati parametre u procesu obrade kako bi se uspio napraviti gotov proizvod traženih dimenzijskih točnosti i svojstava. Problem netočnosti oblika koji je redovito važan česta je istraživačka tema te ga valja adekvatno istražiti (Filho et al., 2009;Kršulja et al., 2012). U procesu obrade deformiranjem dolazi do međudjelovanja geometrija alata tj. žiga i matrice. Položaj alata i matrice je definiran procesnom kinematikom stroja i njegovim mogućnostima.
Putanja alata i utiskivanje lima u matricu određenom brzinom i silom uzrokuje lokalne deformacije koje zajednički djeluju na konačan oblik. Sile u procesu i brzinu kretanja alata potrebno je uskladiti s ponašanjem lima koji se oblikuje (Aleksandrović et al., 2010). Pucanje lima u pojedinim segmentima ovisi o odabranim parametrima u procesu koji negativno utječu na mikrostrukturu. Pri tome je potrebno poznavati mehanizme nastanka dislokacija, ponašanje anizotropije te općenito ponašanje kristalnih zrna prije, tijekom i nakon procesa.
Alati i matrice mogu se proizvesti od različitih materijala. Osim u razlici u cijeni, takve razlike mogu pridonijeti i u razlici ponašanja konačnog proizvoda. Dakle, promjenom alata mijenjaju se uvjeti trenja i zagrijavanja s ciljem poboljšavanja mehaničkih osobina materijala (Plančak et al., 2012). U slučaju uporabe istih alata i mijenjaja vrsta limova zbog različitih mehaničkih svojstava i kemijske strukture, može doći do pojave pukotina i grešaka. U ovome istraživanju ispitat će oblici alata potrebnih za proizvodnju čašice visine h = 36 mm, te promjera di = 34,5 mm. Ispitat će se razlike matematičkog proračuna i simulacije metodom konačnih elemenata. Također, jedan od ciljeva je pratiti deformaciju materijala X5CrNiMo17-12-2 te ispitati sile koje utječu na naprezanja u procesu, a zatim i na postizanje konačnog oblika.
2. KEMIJSKA SVOJSTVA
U ovome istraživanju ispitana su kemijska svojstva lima X5CrNiMo17-12-2, oznaka čelika prema EN 10027-2 je W. nr. 1.4401, u nekim slučajevima označava se i s AISI 316. Običan čelični lim namijenjen postupku dubokog izvlačenja mora, uz nizak sadržaj ugljika i malu čvrstoću te visoku istezljivost, imati kemijski obrađenu površinu (tzv. dekapirani lim). Ovim se kemijskim postupkom na površini lima stvara tanki sloj fosfata koji će biti granični sloj i spriječiti izravni dodir čistih metalnih površina materijala i alata, a ujedno je i nosilac maziva koji se redovito rabi u postupku dubokog izvlačenja. Na taj način se sprječava ljepljenje lima za alat ili matricu. Utablici 1 prikazani su rezultati kemijske analize ispitivane epruvete. Ispitivanje je provedeno na Spektrometru GDS500A, Leco (Tehnički fakultet u Rijeci, laboratorij za ispitivanje materijala). Ispitane su tri epruvete i provedena su tri mjerenja na svakoj epruveti. Rezultati prosječno dobivenih vrijednosti pokazuju poklapanje dobivenih rezultata s propisanim standardom.
3. MEHANIČKA SVOJSTVA
Vlačnim se testom utvrđuje međusobna zavisnost naprezanja i deformacije, a koja se prikazuje σ - ε (naprezanje - deformacija) dijagramom. Epruveta se pod aksijalnim opterećenjem razvlači do loma. Tijekom razvlačenja, materijal epruvete pruža otpor i epruveta se produljuje. Na dijagramu se zapaža točka najveće vlačne čvrstoće, a taj je trenutak praćen značajnim suženjem presjeka epruvete. Nakon toga dolazi do daljnjeg produljenja epruvete što je popraćeno smanjenjem čvrstoće materijala te konačno do loma. Plastično ponašanje materijala započinje kada se ustanove trajne i nepovratne deformacije. U standardiziranim ispitivanjima, zbog poteškoće određivanja točke tečenja kod materijala koji nemaju izraženu granicu tečenja, koristi se naprezanje Rp0,2 (σ0,2), tj. naprezanje pri kojemu ostaju trajne deformacije od 0,2 % (ε = 0,002). Dimenzije epruveta su standardizirane.
U stvarnom se dijagramu naprezanje-deformacija ponašanje materijala može opisati tzv. Holloman-Ludwigovom relacijom. Jednadžba koja se koristi u području proporcionalnosti je Hookeova relacija:
gdje je:
σ - naprezanje, E - Youngov modul elastičnosti, ε - deformacija. Relacija kojom se opisuje ponašanje materijala pri tečenju često se piše u obliku:
što predstavlja tzv. Holloman - Ludwigovu relaciju. U području tehnologije obrade materijala zapis se ove relacije može naći i u obliku:
U izrazima (2 i2a), prva veličina lijeve strane (σ odnosno kf) predstavlja naprezanje tečenja, C je faktor materijala, dok je ε odnosno φ - deformacija. Pri procesima plastičnih obrada izradaka, kada se pojavljuju velike deformacije, za njihov se opis rabi geometrijska deformacija. Nadalje, eksponent očvršćivanja n može imati vrijednosti od n = 0 (idealno plastičan) ili n = 1 (elastičan). Za većinu metala eksponent očvršćivanja n ima vrijednosti između 0,10 i 0,50. Na veličinu faktora materijala C i eksponenta očvršćivanja n utječe vrsta materijala, brzina deformacije, temperatura te veličina i oblik kristalnog zrna.
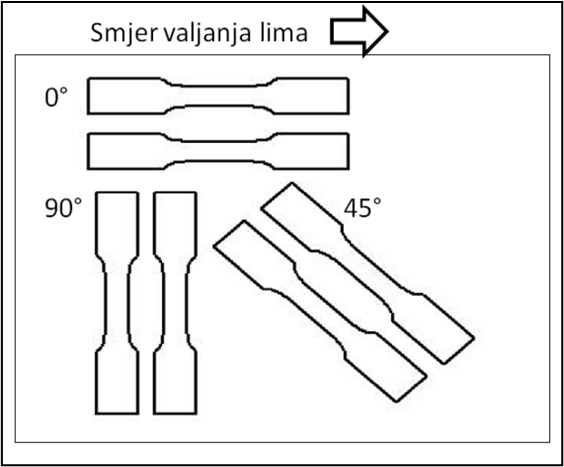
Grafikon 1 prikazuje metodu izrezivanja epruveta kod ispitivanja jednoosnog stanja naprezanja i ponašanje materijala pri različitim kutovima 0°, 45° i 90° od smjera djelovanja opterećenja valjanja. Smjer orijentacije valjanja lima prilikom njegove proizvodnje ima značajne posljedice (anizotropija) u operacijama dubokog izvlačenja. Svojstva valjanih ploča kod većine metala nisu uvijek jednolike u svim smjerovima, te se pomoću mikroskopa može primijetiti da su zrna u mikrostrukturi usmjerena u smjeru valjanja odnosno postoji određeni stupanj anizotropije. Točna povijest određene anizotropije ovisi o kemijskom svojstvu materijala te procesu izrade (tj. ljevanje, valjanje, izvlačenje, žarenje itd.).
Koeficijent anizotropije obilježava se slovom r, naziva se još i Lankfordovim koeficijentom koji izražava omjer poprečnog naprezanja i debljine. Koeficijent r daje dobru procjenu o sposobnosti lima da se deformira u obliku dubokog izvlačenja (r0 ≠ r45 ≠ r90). Greška koja nastaje zbog anizotropije je ušičavost. Poznavanjem anizotropije materijala možemo eliminirati pojavu ušičavosti koja rezultira škartom i općenito lošom iskoristivosti materijala. Koeficijent anizotropije r izračunava se prema (Poverzanović, 1996):
gdje je:
φb - deformacija širine lima, φt - deformacija debljine lima, b0 - početna širina ispitivane epruvete, b - širina ispitivane epruvete poslije deformacije, l0 - početna duljina epruvete i l - duljina epruvete poslije deformacije. Debljina lima se dobiva prema zakonu o konstantnosti volumena l0∙b0∙t0 = l∙b∙t = konstantno.
Anizotropija se otkriva pomoću ispitivanja vlačne čvrstoće te se označava koeficijentima r0, r45 i r90, prema izrazu (4) dobiva se srednja vrijednost koeficijenta normalne plastične anizotropije rs:
Na temelju relacije(4) za duboko izvlačenje metalnih limova tolerancija je rs = 0,8 – 6, a za izotropne limove rs = 1 (Davis 2004). Koeficijent ravninske anizotropije je mjerilo Δr koje govori kakvo je odstupanje normalne plastične anizotropije na kut α. Kut α predstavlja smjer odrezivanja epruvete iz lima u odnosu na smjer vučenja lima, tako da je r = r(α). Kada bi izraz (5) bio Δr = 0, materijal bi se u svim smjerovima jednako rastezao.
Anizotropija ovdje ima značajnu ulogu pri izračunu faktora materijala C te eksponenta očvršćivanja n za ispitivani lim. Pri izračunu je potrebno uzeti u obzir orijentaciju ispitnih epruveta u smjerovima 0°, 45° i 90° kako bi se definiralo ponašanje lima u postupcima deformiranja. Pri tome se faktor materijala C te eksponent očvršćivanja n izračunavaju prema izrazu (6), izračun srednje vrijednosti vrijedi i za Rp i Rm, (Gologoranc, 1991):
U ovome istraživanju provedeno je ispitivanje vlačne čvrstoće, testiranja su napravljena na kidalici Amsler (na Strojniškom fakultetu u Ljubljani, Laboratorija za preoblikovanje). Odabrana je veličina standardne epruvete za limove 250 x 30 mm prema EN ISO 6892-1. Metalni limovi su rezani vodenim mlazom te je izrezano 5 epruveta u svakome smjeru 0°, 45° i 90° u odnosu na smjer valjanja premagrafikonu 1.Grafikon 2 prikazuje rezultate ispitivanja epruveta, ovisno o kutu prema kojemu su rezane 0°, 45° i 90°. Može se primijetiti da se rezultati ne poklapaju.
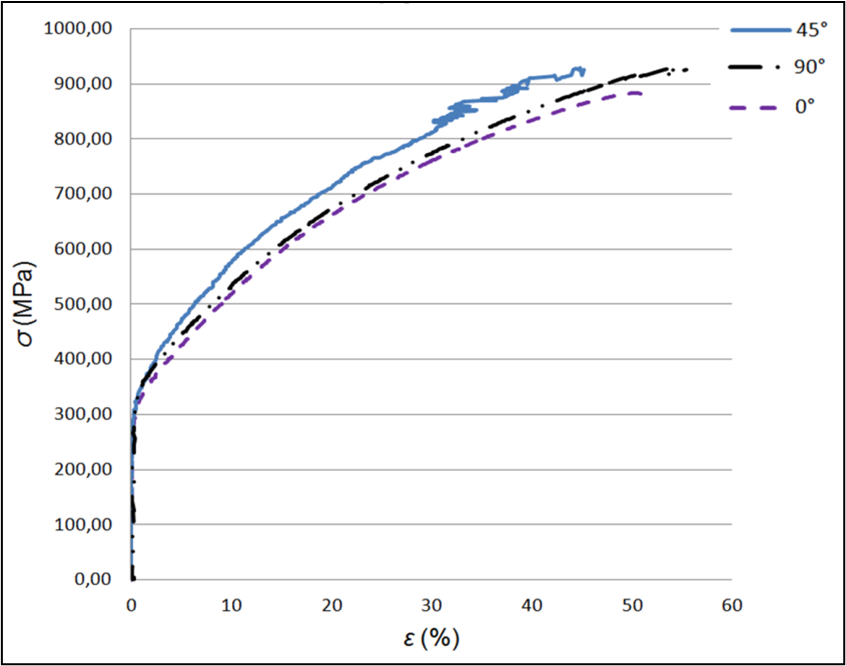
Izvor: obrada autora
Tablica 2 prikazuje mehanička svojstva, Rp0,2 naprezanje pri kojemu ostaju trajne deformacije od 0,2 % (ε = 0,002), Rp0,5 naprezanje pri kojemu ostaju trajne deformacije od 0,5 % (ε = 0,005), A je postotak produljenje epruvete u odnosu na smjer istezanja, A80 prikazuje izmjereno izduženje pri kojemu je došlo do loma, σm = Rm predstavlja vlačnu čvrstoću, r10 , r20 predstavljaju vrijednost koeficijenta anizotropije pri produljenju od 10 i 20 % (budući da r ovisi o ukupnoj deformaciji, preporuka je da se koristi 20 %). Srednja vrijednost koeficijenta normalne plastične anizotropije (rs) za ispitivani lim iznosi 0,864, te prema toleranciji za standardne limove 0,7 - 2,8 ulazi u toleranciju materijala koji je pogodan za tehnologiju dubokog izvlačenja (Davis, 2004). Koeficijent ravninske anizotropije iznosi Δr = - 0,198, a takav rezultat nas upozorava da će rub čašice biti neravan.
Izvor:Kršulja 2012.
Nagrafikonu 3 prikazana je rezultirajuća krivulja tečenja koja će se koristiti za simulaciju ponašanja materijala u softverskom rješenju Abaqus.
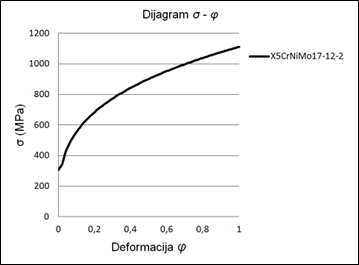
Izvor: obrada autora
Krivulja je izračunana prema Holloman-Ludwigovom relaciji 2a:
Krivulja je rezultat anizotropije, međusobnog djelovanja zrna u mikrostrukturi koji pružaju zajednički otpor naprezanju.
4. PRORAČUN DIMENZIJA ALATA
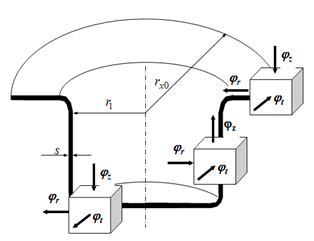
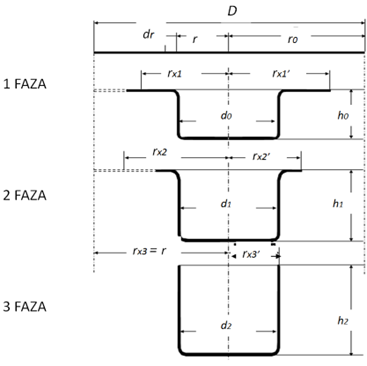
Početni je oblik materijala za obradu ravna ploča koja se označuje kao platina (u obliku kruga ona se naziva rondela). Oblik ove razvijene ploče-platine može biti: krug, kvadrat, pravokutnik, elipsa ili specijalan oblik (zatvorena konturna krivulja) koja zavisi od oblika izvučenog izratka. Principijelno duboko izvlačenje proces je koji se provodi u više faza i kroz nekoliko alata, međutim, kod nekih vrsta limova i jednostavnih geometrija, moguće je do gotova izratka doći i u jednoj fazi izvlačenja. Pri tome obično nema promjene debljine lima, tj. pretpostavlja se da debljina lima ostaje konstantna. Ipak, u stvarnosti dolazi do smanjenja debljine stjenke u blizini dna posude, a pri rubu se događa zadebljanje lima. Nagrafikonu 4 prikazano je deformacijsko stanje u procesu dubokog izvlačenja.
Nagrafikonu 5 prikazane su čašice izrađene od materijala DC03 debljine 2 mm te predstavljaju konačan proizvod. U ovome istraživanju potrebno je izračunati geometriju alata kojom se postižu iste dimenzije proizvoda. S materijalom DC03 dimenzije su postignute u dva koraka (grafikon 5). Materijal DCO3 ima veću sposobnost oblikovanja i ponaša se prema rezultirajućoj krivulji:
testiranja na DC03 su napravljena na kidalici Amsler (Strojniški fakultet u Ljubljani, Laboratorij za preoblikovanje). U istraživanju prema literaturi (Kršulja, 2012) dokazano je da isto nije moguće s materijalom X5CrNiMo17-12-2, već je potrebno izvršiti obradu u tri koraka (grafikon 6). Obrada u tri koraka podrazumijeva izradu tri nova alata. Dobra je praksa, osim proračuna, izvršiti i simulaciju metodom konačnih elemenata kako bi se unaprijed ustanovilo ponašanje materijala i novih alata.
Potrebne dimenzije konačne čašice jesu visina h = 36 mm, te promjer di = 34,5 mm. Potrebna ulazna rondela ima početnu debljinu 2 mm i iznosi D = 70,48 mm, a D = 71 mm je odabrana te se izračunava prema sljedećem izrazu (Musafia, 1969):
Raspon kod dubokog izvlačenja za čelični lim u prvom izvlačenju odabire se tablično β ≈ 1,85 - 1,72 te β ≈ 1,33 - 1,28 u drugom izvlačenju (Musafia, 1969). Za stupanj izvlačenja kod prvog izvlačenja odabran je β = 1,66, te prema (10) iznosi da je unutarnji promjer d0 = 43 mm.
Kod dubokog izvlačenja oblikovanje se provodi na dva načina: prvi način je bez upotrebe stezne naprave (držač, tlačni prsten), dok se njenom upotrebom ploča lima drži tijekom cijelog vremena obrade. Nakon obrade, lim se oslobađa iz stezne naprave, a viškovi potrebni za stezanje se kasnije odrezuju. Pritom držač (tlačni prsten) sprečava pojavu nabora na rubu izratka što je posljedica djelovanja posmičnog naprezanja na relativno tankostjene rondele. Kod relativno debelostjenih i plitkih rondela nema opasnosti od pojave nabora, tako da se u ovom slučaju proces izvodi bez upotrebe držača. Njegova neophodnost ovisit će, prema tome, o vrijednosti omjera d0/s i d1/d0, a prema podacima iz literature (Barišić, 2002) može se odrediti na osnovi izraza:
iz čega slijedi da se za izvlačenje plitkih posuda, kada je lijeva strana jednadžbe veća ili jednaka desnoj, može raditi bez držača i s jeftinijim alatom. U tom slučaju, matrici se na ulaznoj strani daje oblik blagog konusa, što u izvjesnoj mjeri također pridonosi izbjegavanju nabora. U ovom istraživanju za D = 71, s = 2 te d0 = 43 slijedi da je 2,81 > 1,777 te nije potreban držač lima.
Za drugo izvlačenje odabran je koeficijent β = 1,136, te je rezultirajući d1 = 38 mm.
Treće izvlačenje je odabrano kako bi se postigle konačne dimenzije β = 1,11 te je konačna dimenzija d2 = 34,5+0.3 mm. Iako je raspon kod dubokog izvlačenja za čelični lim u prvom izvlačenju β ≈ 1,85 - 1,72, te β ≈ 1,33 - 1,28, u drugom izvlačenju za ispitani materijal stupanj veći od β = 1,66 uzrokovao je lom. Prema promjerima konačnih dimenzija izračunane su preporuke (Musafia, 1969) za konačnu geometriju matrice dp za prvi, drugi i treći korak:
Razmak između žiga i matrice moguće je izračunati iz više izraza, međutim, zbog poteškoća koje se javljaju kod jako tankih limova koji imaju manju debljinu od 0,3 mm, u ovome istraživanju izračunan z = 3 mm prema izrazu:
Najmanja potrebna sila koju je potrebno primijeniti da bi se proizveo proizvod, a da se ne koriste držači lima, izračunana je iz niza izraza 13 - 18 (prema Kuzman et al., 1989). Rezultirajuća sila FM = 19101 N, prema podacima prikazanim utablici 2 s mehaničkim svojstvima. A0 = 282 mm2 ; β = 1,65; n = 0,3015; C = 1111,65 MPa; σfsr = 463 MPa (premaKršulja et al., 2012).
Maksimalna potrebna sila žiga kako bi se izvršila deformacija: FFM ·1,3 = 24,831 kN.
5. MODELIRANJE METODOM KONAČNIH ELEMENATA U SOFTVERU ABAQUS
Matematički proračun daje općenit odgovor na ponašanje materijala te ne uzima u obzir mehanička svojstva poput metode konačnih elemenata koja uzima u obzir krivulju naprezanje-deformacija (σ - φ), gustoću čeličnog lima ρ = 7,850 kg/m3 , Poissonov koeficijent (0,3), Youngovog modul elastičnosti (210 GPa), koeficijent trenja μ = 0,14 (mineralno ulje). Krivulja naprezanje-deformiranje aproksimirana je pomoću Holloman-Ludwigove relacije iz eksperimentalno dobivenih rezultata vlačnog testa (7) te je unesena u softver. Kao metoda izračuna korištena je funkcija ABAQUS/Explicit koja ne zahtijeva izračunavanje uzastopnog sistema jednadžbi ili izračunavanje globalne matrice krutosti. Umjesto toga, traži se dinamička ravnoteža od jednog inkrementa do drugog. U ovome istraživanju odabrana je simulacija ABAQUS/Explicit metodom zbog složenosti procesa obrade u kojemu dolazi do istovremenog pomaka 3 alata.
Metoda konačnih elemenata je matematička tehnika potpomognuta računalom. Konačni elementi mogu biti jednodimenzijski, dvodimenzijski ili trodimenzijski. U ovome radu bit će prikazano trodimenzijsko modeliranje s ljuskastim elementima (S4R), engl. „shell element“, s pet točaka integracije debljine lima (Simpson metoda izračuna). Upotreba ljuskastih elemenata umjesto 3D solid elemenata omogućava brži proračun te manje zahtjevno računalo. Literatura (Abaqus/CAE User's Manual, 2010) upućuje na upotrebu ljuskastih elemenata čija upotreba u simulacijama daje dobar odnos točnosti i vremena proračunavanja interakcije elemenata. Čvorovi i elementi tvore mrežu konačnih elemenata koji opisuju ispitivano tijelo. Svaki element predstavlja dio fizičke strukture čiji ukupan broj utječe na gustoću mreže. Gustoća mreže utječe na rezultate koji se dobivaju analizom. Vrijeme potrebno za analizu ispitivanog tijela ovisi o količini informacija koju treba proračunati i snazi procesora koji se koristi. Optimalno vrijeme potrebno za proračun ponašanja modela ovisi o usporedbi dobivenih podataka s provedenim eksperimentalnim ispitivanjem.
Korištena je mreža s 1240 čvorova i 1200 elemenata, gdje je geometrija rondela dopustila 1166 linearnog četvrtastog elementa tipa S4R te 34 elementa linearno trokutastog tipa S3R. Prema dobivenim podacima iz proračuna, postavljeni su alati premagrafikonu 7 u softverskom rješenju Abaqus. Simulacija je izvršena simultano u tri koraka bez zaustavljanja.
Problem pomaka alata u simulaciju nakon izvršenog djelovanja sile smanjen je postavljanjem uske tolerancije između promjene aktivnih matrica te usklađivanjem brzina žiga.
U istraživanju (Kršulja et al., 2012) prikazan je analitički model izrade u 3 izvlačenja. Uvrštenjem tih dimenzija u numeričku simulaciju dolazi do kontrole analitičkih rezultata. Problem koji se pojavio je gužvanje lima. Dakle, simulacija je ukazala na pojavu gužvanja lima, engl. „wrinkling“; nastanak gužvanog lima može se vidjeti nagrafikonu 8. Osim što obradak ostaje zaglavljen u alat, može doći i do oštećenja alata prilikom same obrade ili skidanja obratka iz alata. U nekim slučajevima dolazi i do trajnog oštećenja alata, što je jedan od dokaza zašto je simulacija dobra praksa u projektiranju alata.
Pomoću simulacije potrebno je pronaći idealan radijus alata žiga i matrice. Izračun idealnog odnosa ulaznog alata žiga i radijusa matrice varira zbog velikog odnosa faktora koji se proizvoljno uzima u jednadžbama za njihov izračun:
gdje je rž radijus zaobljenja žiga i rm = dp/2 radijus zaobljenja matrice. Radijus zaobljenja žiga „r ž “ nikako ne smije biti manji od radijusa matrice „rm“ jer inače postoji opasnost od prosijecanja lima od strane žiga. Radijus zaobljenja matrice za izvlačenje zavisi od oblika dijela i debljine lima. Za izračunavanje približne vrijednosti „rm“ može se koristiti izraz:
gdje je s0 debljina lima.
Iz tog razloga upotrijebljena je simulacija kako bi se definirala optimalna alatna geometrija. Idealna kombinacija radijusa alata dobivena nakon provedenih simulacija prikazana je u tablici 3 te ugrafikonima 9,10 i11. U početnim simulacijama, visina žiga bila je jednaka i u praksi je dovoljno da je hž2 =38 mm. U drugoj fazi, zbog jednake visine žiga kao u 3 fazi, od 38 mm dolazilo je do preklapanja žigova, ulaza žiga u materijal i rezanje ispitivanog materijala. Zato je za potrebe simulacije u trećoj fazi odabrana visina žiga hž3 = 43 mm.
| Faze izvlačenja | rm / rž (mm) | dp / dž (mm) | hm / hž (mm) |
|---|---|---|---|
| 1 Faza | 15/20 | 43/37 | 40.5/33 |
| 2 Faza | 10/15 | 38/32 | 46/38 |
| 3 Faza | 5/15 | 36,5/30,5 | 41/43 |
Izvor: obrada autora
Nagrafikonu 9 prikazana je geometrija matrice lijevo i žiga desno za prvu operaciju deformiranja.
Nagrafikonu 10 prikazana je geometrija matrice lijevo i žiga desno za drugu operaciju deformiranja.
Nagrafikonu 11 prikazana je geometrija matrice lijevo i žiga desno za treću operaciju deformiranja.
6. REZULTATI SIMULACIJE
Nagrafikonu 12 prikazano je rezultirajuće Von Mises stanje (izraz 21) naprezanja u prvoj fazi izvlačenja lima X5CrNiMo17-12-2.
Prema podacima prikazanim na slici može se primijetiti da se najveće naprezanje 845 MPa pojavilo na rubovima čašice. Također, može se vidjeti linija nedeformiranog dijela na sredini čašice gdje naprezanje nije prelazilo 330 MPa.

Izvor: obrada autora
Nagrafikonu 13 prikazano je rezultirajuće Von Mises stanje naprezanja u drugoj fazi izvlačenja za lim X5CrNiMo17-12-2. Najveće naprezanje iznosilo je 1021 MPa što je jako blizu najviše dozvoljenog naprezanja od 1111,65 MPa.
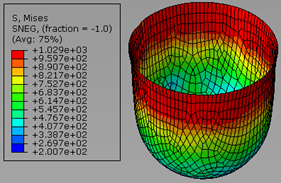
Izvor: obrada autora
Nagrafikonu 14 prikazano je rezultirajuće Von Mises stanje naprezanja u trećoj fazi izvlačenja za lim X5CrNiMo17-12-2. Najveće naprezanje iznosilo je 1064 MPa, što je također jako blizu najviše dozvoljenog naprezanja od 1111,65 Mpa, ali još uvijek u granicama tolerancije.
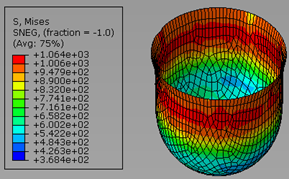
Izvor: obrada autora
Prema rezultatima nagrafikonu 12,13 i14 može se primijetiti da nema pojave gužvanja materijala.
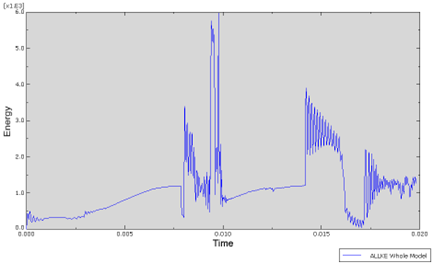
Nagrafikonu 15 prikazano je ponašanje kinetičke energije tijekom simulacije u prvoj, drugoj i trećoj fazi. U prvoj fazi u Ek1 = 6·103 Joula, u drugoj fazi Ek2 = 4 ·103 Joula i u trećoj fazi Ek3 = 2,5 ·103 Joula. Premagrafikonu 15 može se vidjeti da je u prvoj fazi utrošena veća kinetička energija za postizanje deformacije nego u drugoj i trećoj fazi. Iako su pomaci u trećoj fazi manji nego u prve dvije, zbog očvrsnutog materijala potrebno je uložiti značajnu energiju kako bi se ostvarila deformacija.
7. ZAKLJUČAK
Cilj ovoga rada bio je usporediti analitički model sa simulacijom i identificirati radijuse alata i matrice potrebne kako bi se dimenzije konačnog proizvoda zadovoljile. Ispitana su kemijska svojstva materijala te je on zadovoljio standard. Ispitana su mehanička svojstva materijala te se može primijetiti kako materijal ima 306 prosječnu vrijednost granice tečenja, što je 66 MPa više od standarda. Ispitana vlačna čvrstoća iznosila je, u prosjeku, 519 MPa što je niže od propisanog standarda koji se kreće u rasponu od 530 - 680 MPa. Rezultirajući faktor materijal C iznosio je 1111,65 MPa, a eksponent očvršćivanja n = 0,3015 i nalazi se unutar standarda koji se za čelične limove kreće u rasponu od 0,1 do 0,5. Simulacija je pokazala kako uvjeti propisani matematičkim modelom dovode do nastanka greški, gužvanje lima te nastanak pukotine. Mala ušičavost je pretpostavljena prema dobivenom vlačnom testu budući da je Δr = - 0,198, međutim simulacija je pokazala da se pravilnim odabirom radijusa alata može izbjeći pojava ušičavosti. Ušičavost na predstavlja gubitak, to je dodatak materijala na ulaznoj rondeli koji se naknadno odrezuje. Matematički model ponudio je početni radijus matrice od 10 mm, a alata 30 mm, što je dovelo do pojave gužvanja. Literatura preporučuje kako radijus žiga treba biti tri do četiri puta veći od radijusa matrice. U ovome istraživanju pokazana je idealna kombinacija rm/rž =10/15, što je povećanje radijusa žiga od 33 % i ne slijedi preporuku prema proučenoj literaturi. U budućem istraživanju provest će se izrada alata i eksperiment izrade čašica u svakoj fazi dubokog izvlačenja. Usporedba rezultata simulacije i stvarnog eksperimenta potvrdit će vjerodostojnost proračuna i doprinijeti većem uplivu u ponašanje metala pri dubokom vučenju.