1. INTRODUCTION
In the European Union, agriculture maintains its consistently significant role, it is therefore equally significant that agricultural efficiency be measured properly. EU Member States differ in terms of their level of development and – therefore – the efficiency with which they utilize their resources and make investments. With regard to the financing of agriculture, the Common Agricultural Policy has changed over the years in line with the assumptions of such reforms as „Agenda 2000”, „Mid Term Reform”, „Health Check”, the direct and indirect payment system, and the coupling of payments according to with non-market (mainly environmental) objectives. The implementation of these policies affects the efficiency and productivity of agricultural activity, and particularly the value of inputs and outputs, the consequences of investment decisions, the risks and the opportunities for growth and development in the sector, which has been emphasized in the papers ofKumbhakar and Lien (2010),Zhu and Oude-Lansink (2010), andQuiroga et al. (2017).
Although the Common Agricultural Policy has become more environmentally and socially responsible, it still needs to be competitive, and that is achieved by an effective and efficient agricultural production (Quiroga et al. 2017). In turn, the European Union’s sustainable development policy pursues the increasing of efficiency through deintensification, by resorting to technological progress and innovation. This means that as long as there are differences in respect of the level of agricultural development between particular regions, the funds designed for supporting agriculture and the implementation of that policy should be kept distributed and absorbed, also on the basis of analyzing the differences between countries in terms the efficiency of the inputs and outputs that they utilize. Therefore, it is essential that efficiency be studied both at the level of farms and countries/regions. The use of differing measurement methods may be the cause of issues, though, which is made even worse by the scarcity of papers comparing the different approaches to the methods and variables to be used for that purpose.
The main objective of the study was to attempt at assessing the technical efficiency of agriculture of EU Member States in three different years, namely 2007, 2011 and 2016. This efficiency pertained to the given country’s entire agriculture, and not just particular farm categories selected with regard to size or production type. The research consisted of two parts. One involved establishing a ranking and singling out typological groups of states similar to each other in terms of the technical efficiency of their agriculture, using Hellwig’s taxonomic measure of development. The other one involved a relative measurement of the EU Member States’ technical efficiency using the DEA (Data Envelopment Analysis) method. The authors of the present study believe that adopting different approaches simultaneously increases the credibility of the study and provides additional knowledge that can be used both in implementing agricultural policy and pursuing individual agricultural business objectives. What is innovative about this research as that it compares the results of two different approaches to assessing the efficiency of agriculture in EU Member States.
2. TECHNICAL EFFICIENCY OF AGRICULTURE IN SCIENTIFIC RESEARCH
Efficiency as a concept does not have a single clear definition, but what is certain about it is that it always describes a positive attribute of the undertaken activities. Its detailed sense is related to the nature of the activity being assessed, the assessing entity, the objectives of the analyses, etc. It is derived from the concepts of productivity and efficiency. In 1957,Farrell asserted that they both referred to the performance of the unit transforming inputs into outputs. He claimed that productivity was the ratio of actual outputs to actual inputs. The so-defined productivity had merely a purely theoretical meaning, as it could only be measured where there was one outcome. Where there were more output and inputs, it was necessary to refer to a different measure, i.e. efficiency. InFarrell’s opinion, efficiency described the relationship between the productivity of the given unit and the productivity of an efficient unit, i.e. the maximum productivity the attaining of which was possible under the given technological circumstances. In turn,T. Coelli et al. concluded in 1998 that the total efficiency of the enterprise was the resultant of the two components: technical efficiency reflecting the enterprise’s ability to reach maximum production using the given group of inputs, and allocative efficiency showing the enterprise’s ability to use inputs in optimum proportions, at established prices and with an established production technology.
According toK.R. Shanmugam and A. Venkataramani (2006), the efficiency of an agricultural farm can also be measured in terms of allocative efficiency (which reflects of the farm’s capability of utilizing inputs in optimal proportions taking into account their relevant prices) and technical efficiency. In their paper, they also studied technical efficiency, defining it as a business entity’s capability and readiness to achieve maximum production (frontier production) with a specific level of inputs and technology. For this purpose, they used a stochastic frontier production function model which allowed them to establish the mean technical efficiency for different agricultural farms.
Similar research was carried out byJ.G. Djokoto, F.Y. Srofenyoh and A. Afrane-Arthur (2016). According to them, the first step on the way to improve technical efficiency was to measure it. They proposed that the relationship should be established between global production and frontier production that allowed for determining the gap between the two, which they called technical inefficiency. In their studies of technical inefficiency, they used meta-regression, determining the technical inefficiency variable as an exogenous variable in the model.
The technical efficiency of agricultural production has also been studied byA. Skarżyńska (2017). In her research, it was established through: an assessment of technical productivity (the productivity of individual factors of production), the technical efficiency of land (measured by the efficiency of the studied plant production activities), the technical efficiency of labor (the volume of production from 1 ha per 1 hour of labor inputs) and the technical efficiency of fixed assets (the volume of production per PLN 100 of the value of the invested fixed capital). This allowed her to compare farms from different regions of Poland in terms of their technical efficiency.
Agricultural efficiency can also be studied using the DEA (Data Envelopment Analysis) method. Literature is rich in reports on measuring this phenomenon with the help of the aforementioned approach, with researchers taking various perspectives, from economic through environmental and social. Such research is carried out at the levels of farms, countries and regions and focuses on diverse types of farms, crops, sizes and other aspects. The ScienceDirect databases render hundreds of search results for the last 10 years for conditions such as ‘agriculture, efficiency DEA’. However, there has not been much research into agricultural efficiency in EU Member States (Martinho, 2017). Most papers at the level of the EU or its regions only adopt one group of methods, with non-parametric methods, mainly DEA, prevailing definitively. Studies byAkande, 2012;Baran, 2016;Błażejczyk-Majka 2011,2017;Bojnec et al. 2014;Cankurt et al. 2013;Iliyasu et al. 2016,Guth & Smędzik-Ambroży, 2019;Gavurova et al. 2019;Kołodziejczak, 2015;Nowak, Kijek, Domańska, 2015;Staniszewski, 2018 andToma et al., 2017, which measured efficiency using various models and various sets of variables, are a number of examples.
Studies using parametric methods that first of all estimate the efficiency curve to be subsequently used as a basis for comparisons between actual units are less abundant in literature. However, there are many more papers adopting SFMs (Stochastic Frontier Models), which usually focus on a single country or region or production type (e.g.Rudinskaya et al., 2019,Quiroga et al., 2017,Zhu et al., 2008 and2011). Extended research using two or more efficiency assessment methods can be found in the papers ofKočišová, 2015;Hoang and Trung, 2013;Marzec, 2019;Vlontzos et al., 2017, and others.
3. DESCRIPTION OF THE STATISTICAL MATERIAL
As mentioned before, the objective of the study was to apply two approaches to assessing agricultural efficiency of EU Member States. One of them made use of the assumptions of the DEA (Data Envelopment Analysis) method. The other involved linear ordering, which means that the synthetic measure of development was first calculated and subsequently used as a basis for establishing a ranking of units and grouping them with regard to the phenomenon studied herein. The obtained results allowed for determining whether there were differences between the results of assessments of the efficiency of individual countries or groups of countries depending on the method applied. EUROSTAT data were obtained for the purposes of the study. Comparisons were made for three periods, namely 2007, 2011 and 2016.
As the two approaches make use of different types of diagnostic criteria, an attempt was made to single out such data that could be used for comparisons. Due to the nature of the DEA method, a model was first constructed that included data concerning the main production factors, such as land, capital and labor. The data were grouped into a set of variables, the combination of which reflected the agricultural production technology in place. The model variables were selected on the basis of a literature review. The following set of variables was adopted: (y1) agricultural production (EUR million), (x1) agricultural area (thous. of hectares), (x2) labor (thous. of AWU), (x3) direct costs (EUR million), (x4) farming overheads (EUR million) and (x5) depreciation (EUR million). Direct costs (x3) included expenses on: seeds and seed potatoes, fertilizers, protection, veterinary applications and feed. The costs under the (x4) variable included expenses on: power, materials, building maintenance, agricultural services and other indirect costs.
A preliminary statistical analysis of these variables showed significant diversity between the individual countries in terms of the scale of their agricultural activity. One of the effects of the preliminary analysis was the adoption of the DEA model that assumes variable returns to scale and is input-oriented. This was in line with the tendencies within the EU sustainable development policy that aims at increasing agricultural efficiency through innovation and deintensification of inputs (Bieńkowski et al. 2013). In turn,Błażejczyk-Majka et al. (2011) claims that efficiency could be increased by reducing labor intensity and invested fixed capital, at the same time increasing outlays on biological, technical and organizational progress, which is in line with the orientation assumed for the model, as well.
Another effect of the preliminary analysis was that three countries, i.e. Cuprus, Luxembourg and Malta, had to be excluded from the study as their variable systems were not sufficiently cohesive with the study group. The agricultural activity models in those countries could be perceived as too distinct for them to be included, which has also been emphasized byFloriańczyk and Rembisz (2012), as well asBaran (2016). This was why – in accordance with the DEA method’s rules – they were ruled out from further study.
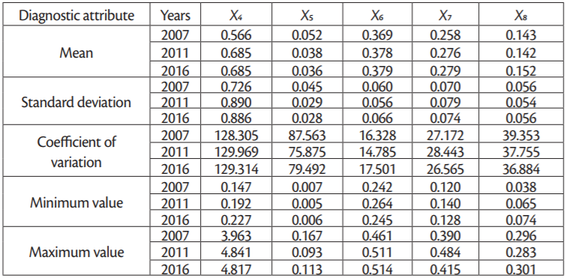
The main descriptive statistics of variables assumed for the model, covering 25 observed countries, are shown inTable 1.

Source: the author’s own study based on the EUROSTAT database.
Basing on the same original data set, a starting set of diagnostic attributes for calculating the synthetic measure of development was defined:

In order to be usable for discriminating the studied units, the diagnostic attributes had to demonstrate substantial variation. Therefore, coefficients of variation were calculated for them according to the following formula (Nowak, 1990):

where:

Subsequently, they were compared to the arbitrarily assumed critical value v*
(in this study v* = 10%).
If there had been such values for which 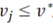 ,
they would have had to be excluded
from the set of potential attributes. However, all the attributes assumed in this study demonstrated
considerable variation, with their coefficients of variation adopting the following value ranges: in
2007 = 16.33%-128.31%; in 2011 = 14.78 % –129.97 % and in 2016 = 17.50 % – 129.31 %. It should
also be added that they were characterized by strong or very strong asymmetry.
,
they would have had to be excluded
from the set of potential attributes. However, all the attributes assumed in this study demonstrated
considerable variation, with their coefficients of variation adopting the following value ranges: in
2007 = 16.33%-128.31%; in 2011 = 14.78 % –129.97 % and in 2016 = 17.50 % – 129.31 %. It should
also be added that they were characterized by strong or very strong asymmetry.
The potential attributes characterizing the agricultural efficiency of EU Member States could be linked with one another, which might have resulted in replication of information about the units. For this reason, the degree of their correlation had to be determined and those attributes that were strongly linked to others needed to be removed. To this effect, a matrix of coefficients of correlation between the attributes was established, on the basis of which attributes were selected for the study using the parametric method proposed by Hellwig (Nowak 1990). The final set of attributes comprised five coefficients: X4, X5, X6, X7, X8. All of them were destimulants, meaning that from the point of view of the studied phenomenon the lower values the more favorable they were. The descriptive parameters for the assumed attributes are shown inTable 2.
4. METHODS AND RESULTS
The methods for ordering the set of objects may be divided into linear and non-linear ones. The former of them allow for establishing the hierarchy of the objects according to a specified criterion. The latter, though, are only used to indicate objects similar in terms of the values of their features (Panek, 2009). Linear ordering methods are in universal use in economic studies, where they are applied to comparisons between units with regard to the studied phenomenon. They can be used for determining the ranking of various units with regard to different phenomena. Procedures based on the synthetic variable are one type of such methods. The linear ordering methods include, among others, also synthetic value-based procedures that use model and nonmodel indicators (Grabiński, 1992;Pociecha et al., 1988). In the non-model methods, the synthetic value is a function of standardized values of the input variables. The model methods, on their part, resort to the concept of the model object, i.e. a model object carrying desired values of the input variables. The synthetic measure is constructed on the basis of a measurement of the distance between the observed object and the model object (Panek, 2009;Tarczyński, Łuniewska, 2006).
In this paper, a classical approach to the model method was used for constructing the taxonomic measure of development. The classical measure of development is based on standardized z_ij values of the diagnostic features, therefore (Nowak, 1990, cf.Bąk, Szczecińska, 2013):
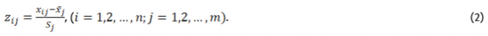
Subsequently, for each studied object its distance from the established model of development is determined along with the formula:

whereas for the stimulants 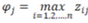 , and for the destimulants.
, and for the destimulants.
The synthetic measure of development is determined using the following formula:

where:

Using both the formula for calculating the synthetic measure of development and the information that the measure’s values range between 0 and 1, the limit for the a constant was determined (Tarczyński, Łuniewska 2006) 1:

The values of the synthetic variable for individual EU Member States, with account taken of the assumed diagnostic attributes, are shown inTable 3.
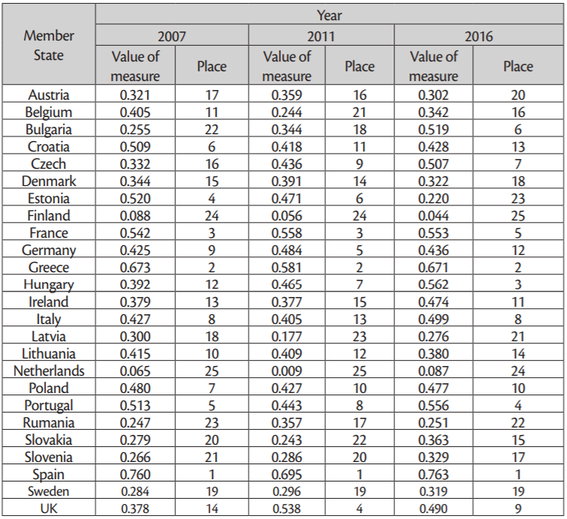
Source: the author’s own calculations.
All three rankings were topped by the same countries: Spain and Greece. They demonstrated the lowest values of such coefficients as farming overheads per unit of revenue, and AWUs per unit of revenue. The lowest raking positions in all the analyzed years were occupied by Finland and the Netherlands. With regard to the X4 and X7 coefficients, these countries exceeded the average for all the units studied by far, and as these coefficients are destimulants their results should be treated as negative.
The three means method (Nowak 1990, p. 93) was used to group units bearing similarities in respect of the studied phenomenon, in line with the following rules:

This method allowed for the set of the EU Member States to be divided into four group encompassing units bearing similarities with regard to agricultural efficiency (Table 4).
Source: the author’s own calculations.
The first group included those EU Member States whose synthetic measure value was higher than or equal to its mean value plus the standard deviation. These countries were assessed as the best from the point of view of agricultural efficiency. In 2007, this group comprised three countries (12 %), in 2001 four countries (16 %) and in 2016 only two countries (a mere 8 % of the total study group). In each of the analyzed years this group demonstrated the lowest mean values for the following destimulants: X4, X6, X7, X8.
The second group included those countries which were assessed as good in terms of the phenomenon studied herein. Depending on the period of study, their number ranged from 9 in 2007 (36 %) to 11 in 2016 (44 %). These EU Member States achieved good results when compared to the overall average values, especially with regard to the X7 and X8 coefficients. They stand a chance of improving their ranking position in the coming years.
The third group was the largest in 2007, when it comprised 11 countries (44 %). In comparison with the other groups, this one demonstrated the worst (highest) mean value for the X5 coefficient and worse mean values than groups 1 and 2 for the X6, X7 and X8 coefficients.
The last group included countries demonstrating the worst efficiency with regard to the analyzed coefficients. Their value of the synthetic measure was lower than the average value minus the standard deviation. Their poor positions mainly stemmed from their least favorable average levels in respect of such attributes as X4 and X8.
The DEA method is based on the concept of productivity authored byG. Debreu (1951) andM.J. Farrell (1957).Farrell created the concept of „efficiency frontier” or „(best practice) production frontier”. This frontier is accepted as the technology frontier of the production capacity achievable for the given decision-making unit (DMU) (in this study, the DMUs are represented by the individual EU Member States). Farrell’s concept provided for measuring the given DMU’s efficiency in relation to other units employing a similar production technology. From a single input and a single output, this idea was subsequently expanded to multi-dimensional cases through the research ofA. Charnes, W. W. Cooper and E. Rhodes in 1978, who proposed a model assuming constant returns to scale, most frequently referred to in literature as the CCR model. With the development of research making use of this method’s assumptions, numerous alternative models and modifications to the original CCR model have been offered. As mentioned before, in this study the input-oriented BCC model assuming variable returns to scale was used (Banker, Charnes, Cooper, 1984).
The efficiency measurement concept applied in the CCR and BCC models makes use of one of the most popular techniques described in, inter alia, the paper titled „Production Frontiers” (Färe et al., 1995). If s – outcomes and m – inputs are available, technical efficiency can be derived using this formula (7):
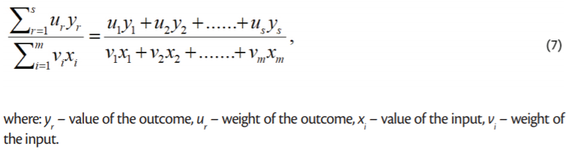
For each unit, a linear programming problem is solved, where the derived efficiency measure takes the form of the objective function subject to maximization, and the variables subject to optimization take the form of the weights of outcomes and inputs. For input-oriented models, it is as follows (8):

with the following constraints (9):
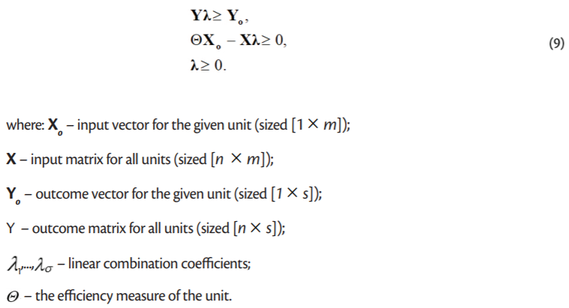
The problem was solved for all n of the units. The purpose of the optimization was to find the minimum value of the efficiency measure for which inputs or resources could be reduced without affecting the level of the output. Where such reduction was not possible, then pΘ = 1, which meant that a more favorable combination allowing the unit to achieve the same outcome did not exist. In that case, the unit was referred to as economically efficient. However, where Θ < 1, there existed a more favorable input combination allowing for the same outcome to be achieved. The Θ parameter determined the percentage of the observed unit’s inputs that was sufficient to achieve the current outcome level using the technology of efficient units. The information on the structure of the optimal input and outcome combination was provided by linear combination coefficients λ (Rusielik, 2017).
In 1984,Banker, Charnes and Cooper proposed that the
CCR model be expanded to the BCC model
assuming variable returns to scale
(Banker, Charnes, Cooper, 1984). For this purpose, the CCR
model can be modified by adding the convexity constraint 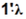 = 1,
which results in the following model (10):
= 1,
which results in the following model (10):

with the following constraints (11):

This assumption causes the efficiency outcomes to be more precise in this model than those obtained under the CCR model assumptions.
For the observed group of 25 UE Member States, technical efficiency measures were derived using the input-oriented BCC model assuming variable returns to scale. The synthetic measurement scores, together with basic statistical data for the entire group of counties subject to comparison, are presented inTable 5.
| Factor | 2007 | 2011 | 2016 |
|---|---|---|---|
| Number of countries | 25 | 25 | 25 |
| Mean | 0.922 | 0.956 | 0.982 |
| Minimum | 0.724 | 0.787 | 0.890 |
| Maximum | 1.000 | 1.000 | 1.000 |
| Standard deviation | 0.088 | 0.056 | 0.029 |
| Efficient countries | 11 | 16 | 15 |
In the studied years, the mean efficiency measure kept growing. In 2007, it was 0.922, and grew to 0.982 by 2016, and so did the minimum efficiency level. The differences in efficiency levels between the observed countries decreased over these years, with the standard deviation dropping from 0.088 to 0.029, as well. The number of countries deemed as efficient grew from 11 in 2007 to 16 in 2011 and dropped to 15 in 2016.
The technical efficiency measures for the individual countries are shown inTable 6. The table also provides the numbers assigned to the groups created using the three means method on the basis of the synthetic measure value.
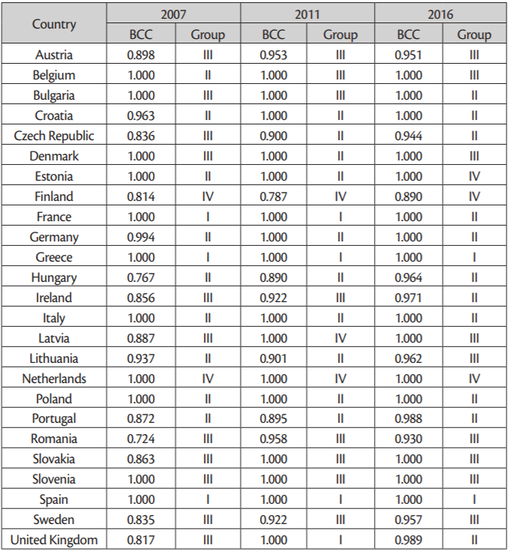
Source: the author’s own study
Our analysis of the efficiency measure levels showed that 11 of the observed EU Member States were efficient. These were Belgium, Bulgaria, Denmark, Estonia, France, Greece, Italy, the Netherlands, Poland, Slovenia and Spain. Three more countries, namely Croatia, Latvia and Germany joined the group of efficient states in 2011 and were still part of it in 2016. The United Kingdom joined the group in 2011, as well, but its efficiency measure dropped slightly in 2016. The remaining countries demonstrated certain levels of inefficiency in all of the studied years. In 2007, the group of lowest efficiency countries included Romania (with an efficiency level of 72.4%), Hungary (76.7%) and Finland (81.4%). In 2011, this group included Finland (78.7%), Hungary (89.0%) and Portugal(89.5%). In 2016, it included Finland (89.0%), Romania (93.0%) and Czech Republic (94.4%).
5. CONCLUSION
The main goal of the research was to assess the effectiveness of agriculture in the European Union. We assumed that this is important because of the significant role it plays in the European economy. Agriculture in the European Union is shaped through the implementation of the Common Agricultural Policy. Financial resources for implementing this policy should also be distributed on the basis of differences in efficiency levels. The problem is that the assessment may differ due to the method used. There are no studies comparing alternative approaches. In our research, we used two different methods and performed an assessment of the level of effectiveness in individual countries. The results of both methods overlap only partially.
Comparison of the results in the first group, the highest rated in terms of effectiveness, using a synthetic measure, is consistent with the approaches used. The average technical efficiency index for this group was 1,000. All countries in this group (Spain, Greece and France) were fully technically effective in all the analysed years. In turn, Great Britain, which was in this group of countries in 2011, in other years was characterized by a certain level of technical inefficiency.
In turn, in the second group, assessed as good in all analysed years, there were countries such as Croatia, Germany, Hungary, Italy, Poland and Portugal. With the exception of Hungary and Portugal, these countries showed full technical efficiency. Three countries, i.e. the Czech Republic, Estonia and Lithuania were classified in this group in two analysed years, and among them Estonia showed full technical efficiency. The average technical efficiency index in this group ranged from 0.948 to 0.980. Unlike the previous group, there are discrepancies between the measurement results obtained using both methods. Over half of the countries can be considered as fully effective, i.e. they should be in the first group.
The third group rated as below the average in all analysed years included the following countries: Austria, Romania, Slovakia, Slovenia and Sweden, while in the two analysed years countries such as: Belgium, Bulgaria, Denmark, Ireland and Latvia. Comparing the results of the effectiveness assessment in this group, one can also notice discrepancies. According to the grouping of the synthetic index, the countries of this group should be characterized by below-average efficiency results, while the technical efficiency index shows that apart from 2007, half or more than half are countries that can be considered effective. The level of the average efficiency index in the analysed years ranged from 0.883 to 0.978 and was close to the level from the second group.
The fourth group, the least numerous one, are countries with an unfavourable level of analysed indicators. Finland and the Netherlands were in this group in all analysed years. In turn, Estonia and Latvia were in this group only in one year. In the case of this group, the level of technical efficiency index also varied. Finland showed one of the lowest performance indicators (0.787 to 0.890), while the Netherlands is shown as a fully effective country, just like Estonia and Latvia.
Studies have shown differences in the assessment of effectiveness between the methods used. It can be assumed that making decisions based on one method or group of indicators may be wrong. In order to use financial resources in a rational manner for the implementation of the Common Agricultural Policy, redistribution of funds for this purpose should be associated with the efficiency of expenditure and resources used, but the assessment of this efficiency should be based on the analysis of the results of alternative measurement methods. At the current stage of the research, the authors are not able to answer what approaches, methods and models are the most reliable. There is no comparative study in the literature. Extending the research by analysing the results of performance assessment using several alternative methods will fill the knowledge gap on this subject. The implemented Common Agricultural Policy, despite changing priorities, will always have to be competitive, i.e. among others, it must be based on effective production. The effects of currently planned decisions related to the new financial perspective will have an impact on the efficiency of the agricultural activities of European manufacturers for many years. Hence the postulate to extend the research by assessing alternative measurement methods. This will increase the credibility of the results and help make better decisions.