Multi-objective Optimization in EDM Process Using Backpropagation Neural Network-Genetic Algorithm (BPNN-GA)

1. Introduction

The process of cutting hard materials with complex shapes requires modern machining methods[1]. One of these modern machining techniques is known as Electrical Discharge Machining (EDM). EDM is the most popular and widely used unconventional machining process because it can produce components with good surface quality and high dimensional accuracy. Moreover, EDM is an economical, unconventional machining process that can be used to machine conductive metals with a high hardness level[2].

In the aerospace, automotive, and stamping industries, metal alloys and cement carbides are usually machined using EDM. During machining, the material is eroded by melting and vaporization caused by the release of energy at the sputtering point, which raises the temperatures at the workpiece surface to a very high level[3]. The most widely used EDM process is EDM sinking, which is used as a tool for mold making and industry[4].

AISI P20 is a material used in mould making industry, and commonly utilized for die casting, moulding of plastics, frames for plastic pressure dies, and hydro-forming tools[5]. Several researchers have used EDM to cut AISI P20 steel[6 and 7].

In the EDM process, several characteristics must be met to create products that meet specifications, among which the most frequently discussed are MRR and SR[8]. MRR is the amount of metal removed in a given time[9]. Reduced machining time further increases production costs. In addition, the SR value becomes a quality that must be achieved. The lower the SR value, the better the product quality. However, the high SR value achieved by EDM machining has a negative effect on fatigue strength[10].

In order to produce high quality, reliable components that meet customer needs, the manufacturing process is expected to implement a more cost-efficient strategy without compromising the quality of the manufactured products. Improving product quality while reducing manufacturing costs requires a decision on the process variables. A precise determination of the process variables is able to achieve optimal machining performance. The most influential process variables in EDM include GV, current, T_on, T_off, and duty factor[11].

Numerous studies have been conducted to determine the most appropriate process variables for optimal MRR and SR. The process variables affecting MRR and SR were current, T_on, and T_off[12]. Singh et al. investigated MRR and roughness in the Die Sinker EDM process using the current, GV, T_on, and T_off process variables[13]. The study by Kumar et al. also found that T_on and T_off affect SR in the Die Sinker EDM process[14].

The common method for determining the level of machining variables is to refer to work experience or machining instructions, although this approach provides unsatisfactory values. Another method of selecting the processing variables is to conduct non-technical trials and experiments[15]. Effendi et al. also found that determining machining variables through experiments is difficult, time-consuming and unaffordable[16]. Therefore, to create models and improve machining performance, researchers have used metaheuristic or soft computing techniques. Artificial neural networks (ANN) have attracted much interest due to interest due to their ability to predict the response of complicated nonlinear systems.

One of the ANNs commonly used to predict the response of the machining process is the Backpropagation Neural Network (BPNN). Models of BPNN that have few inaccuracies can accurately estimate the results[17]. Numerous research works on the application of BPNN have been conducted in various disciplines, especially in the manufacturing process. Models for estimating response variables are frequently generated using BPNN. Chalisgaonkar et al. used BPNN to predict the final characteristics of EDM machining process[18]. Shakeri et al. developed feedforward backpropagation neural networks to predict MRR and SR in wire-EDM processes. There was an error of 0.773 between the experiment results and the prediction. These results indicate that neural networks have a high degree of accuracy[19].

BPNN is often combined with metaheuristic methods to optimize response variables in machining processes. In the WEDM process, Zhang et al. integrated BPNN and GA to optimize process variables for surface integrity[20]. Soepangkat et al. also used the BPNN-GA combination for response optimization in the WEDM process[21]. Saffaran et al. applied hybrid BPNN and PSO methods to achieve optimal performance of die-sinking EDM processby maximizing MRR and minimizing tool wear rate (TWR) and Mohanty et al. applied the same method to increase MRR and reduce TWR, SR and radial overcut[11 and8].

According to the above-mentioned literature review, there are no studies on multiresponse optimization in the sinking EDM process performed using the two hybrid BPNN-GA methods. Therefore, this study aims to investigate the level of variables of the sinking EDM process on AISI P20 that produces an optimal response, including minimizing SR and maximizing MRR. The backpropagation neural network method is used for modelling, while multi-objective optimization is performed using genetic algorithm (GA).

2. Experimental procedure

2.1 Material and machining condition

The machining process was utilized on the EDM Sinking Aristech ZNC EDM LS 550. The material was AISI P20 with dimensions of 25mm × 25 mm × 20 mm. The depth of the cut was 0.5 mm. The EDM process variables were electrode type, gap voltage (GV), pulse on time (T_on), and pulse off time (T_off). The values and their levels are summarized in Table I. The variables consisted of two levels for the electrode type and three levels for GV, T_on, and T_off. The responses investigated were SR and MRR. The SR value was measured with the Mitutoyo SJ-310. The MRR was expressed as a ratio between the weight loss of the workpiece and the duration of the machining operation, as shown in Formula 1[22]. The difference between the workpiece's pre and post-experiment was the amount of weight loss.

[TeX:] \text{MRR} = \frac{W_{f} - \ W_{i}}{t}$\mathrm{\text{MRR}}=\frac{W_f-W_i}{t}$ (1)

where W_f and W_i are the final and initial weights of the workpiece, respectively, and t is the period of the machining process.

Table 1 EDM Cutting Variable

2.2 Experimental design

The Taguchi method-based L₁₈ orthogonal array was applied in the experimental design. Table 2 shows the L₁₈ orthogonal array with 18 experimental combinations. experiments on EDM were randomized with two replications. The experimental data were subjected to an ANOVA test to see the influence of process parameters on response parameters. Next, the experimental data were used for modelling using BPNN. The BPNN results in the form of an objective function were then used as a fitness function in optimization. The steps for using the BPNN-ABC method are shown in Figure 1.

Table 2 Orthogonal Array L₁₈

3. Modelling and optimization

3.1 Backpropagation Neural Network

Rumelhart et al. (1985) initially introduced BPNN in 1985. The BPNN model is considered the most efficient method for modelling different cases. Before modelling, data on process variables and response measurements are first normalized with a constraint of -1 and 1. The normalizing calculation is included in Formula 2[23].

[TeX:] N = \left( 2 \times \frac{(E_{\text{xp}} - \min\left( E_{\text{xp}} \right))}{(\max\left( E_{\text{xp}} \right) - \min\left( E_{\text{xp}} \right))} \right) - 1$N=(2\times \frac{(E_{\mathrm{\text{xp}}}-min\left(E_{\mathrm{\text{xp}}}\right))}{(max\left(E_{\mathrm{\text{xp}}}\right)-min\left(E_{\mathrm{\text{xp}}}\right))})-1$ (2)

where the normalized process parameter and response parameter data results are represented by the variable N, and E_xp is the data level of the process variables, and the response used from the measurement results.

The input layer, hidden layer, and output layer constitute the BPNN. Neurons in each layer connect within layers. The network architecture with the smallest mean square error (MSE) is found through the approach of trial and error. This process begins with determining the BPNN parameters, such as the total amount of hidden layers and neurons.

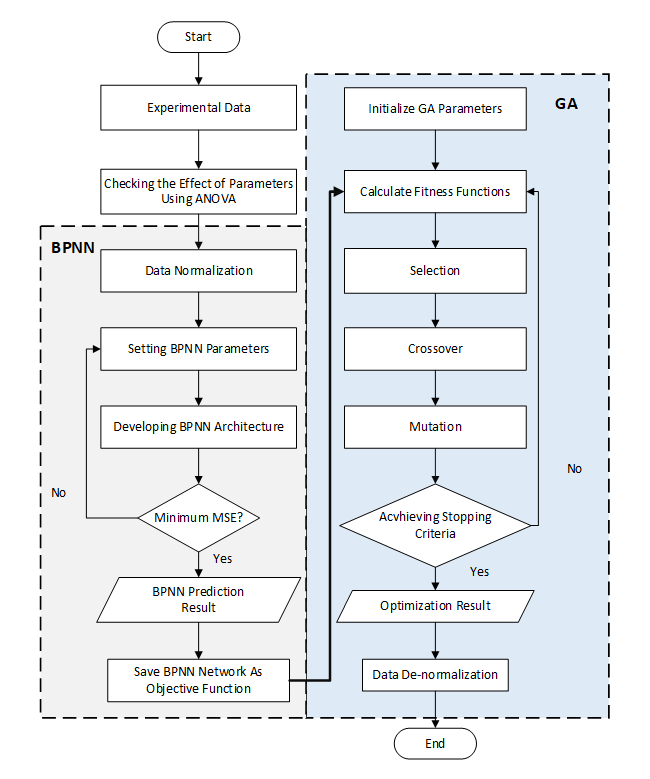
Fig. 1 Flowchart

Training, testing, and validation data usage proportions are 70%, 15%, and 15%, respectively[16]. Due to its rapid convergence rate when compared to other training techniques, the Levenberg-Marquardt (LM) algorithm is chosen for training[24]. Formula 3 is used to obtain the error value, which is then used to compare the BPNN prediction results with the experimental values[25]. The resulting BPNN model and objective function are stored and applied to optimize the response variables.

[TeX:] \text{Error} = \left| \frac{D_{\text{Exp}} - \text{BPNN}}{D_{\text{Exp}}} \times 100\% \right|$\mathrm{\text{Error}}=|\frac{D_{\mathrm{\text{Exp}}}-\mathrm{\text{BPNN}}}{D_{\mathrm{\text{Exp}}}}\times 100\%|$ (3)

where D_Exp indicates the experimental value and BPNN the predicted value.

3.2 Genetic Algorithm (GA)

GA is an optimization technique that refers to the concept of natural evolution. GA techniques are mainly applied to solve problems related to optimization, which can determine the optimal global solution. The GA process begins with an initial solution set consisting of several components or genes known as chromosomes. According to some principle or by randomness, the initial population of chromosomes is created. After the initial population is evaluated based on the fitness function, new solutions are applied for a new population. Several GA procedures are performed to generate new populations, including selection, crossover, and mutation[26]. Previous population solutions are chosen based on suitability, suitability, and probability of being selected. The selected solution creates a group of parents who are used to produce offspring. Through mutations and crossovers, the offspring produced new populations[27].

The procedures required in the GA optimization process include randomly initializing the population, evaluating objective functions, determining fitness functions, and applying genetic parameters such as selection, crossover, and mutation until the process meets the termination criteria.

4. Results and discussion

4.1 Effect of process variables

The goal of the ANOVA test was to identify the process variables that significantly affected the response. The ANOVA test was carried out using experimental data. ANOVA was carried out on each response with a significance value (α) of 0.05. A process variable is significant to the response when it has a P-value less than 0.05 at the 95% confidence level. The percentage of contribution was used to determine the contribution of various process variables to the responses towards the total variance.

According to Table 3 from the implementation of the ANOVA to variations in MRR, all of the variables analysed, including the type of electrode, GV, T_on, and T_off, have a P-value less than 0.05 at the 95% confidence level. As a result, it could be said that these variables were significant for the MRR. Among the variables employed in the present study, T_on had the largest percentage contribution of 22.32%. Additionally, other variables including type of electrode, GV, and T_off had less contribution with respective contributions of 18.39%, 12.61%, and 11.68%. For SR based on Table 3, Remark, the type of electrode was the most important variable, contributing 53.16% of the total variance. T_on and T_off took second and third place, contributing 35.01% and 3.73% of the total variance, respectively. At the same time, GV did not significantly contribute to SR.

Table 3 confirms that T_on and T_off significantly affect the MRR and SR values. The same findings that T_on and T_off were the main variables affecting the MRR and SR values in the EDM sinking process were reported by Dikshit et al.[2] and Bédard et al.[28]. In addition to T_on and T_off, the electrode type was also found to affect significantly MRR and SR[29].

The EDM sinking process produces surface contours in the form of craters and ridged surfaces. The craters on the surface were formed as molten material that was blasted out of the surface due to the discharge pressure. Then the molten material was submitted tocooling by the dielectric fluid. Large crater sizes produced higher surface roughness. Also, deep craters indicated a high metal removal rate and poor surface roughness[30].

Table 3 ANOVA for Material Removal Rate (MRR) and Surface Roughness (SR)

Figures 2 and 3, respectively, show graphs that demonstrate the effect of the process variables for MRR and SR. Figure 2 indicates how the use of copper electrodes increased MRR. Kuppan et al. came to same conclusion[31]. The greatest MRR value was reached by GV at the intermediate level, whereas the increase of T_on and T_off caused the decrease of MRR. More energy was released at a longer T_on, which led to a more powerful discharge and resulted in a high metal removal rate with deep craters on the surface of the workpiece. However, Figure 3 shows that as T_on increases, the MRR decreases. This may be caused by excessive melting of the material, which causes build-up between the tool and the workpiece, and the MRR to decrease[2]. The high level of T_on delivered less energy to the surface during machining due to material build-up, resulting in low MRR. On the other hand, a spark disappeared during the T_off period, so the cutting process did not occur. A low T_off value would increase the machining speed, which might raise the MRR.

In addition, Figure 3 demonstrated that employing graphite electrodes reduced the SR[32]. The SR value was lowered as GV and T_on were enhanced[33]. Furthermore, a high T_off caused the increase of SR. This possibly happened because some of the molten metal did not wash with the dielectric fluid but re-deposited on the surface and later produces a higher surface roughness.

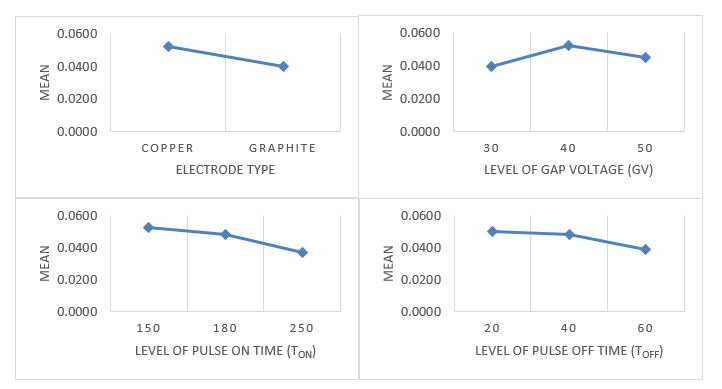
Fig. 2 Response Graphs for the Mean Values of Material Removal Rate (MRR)

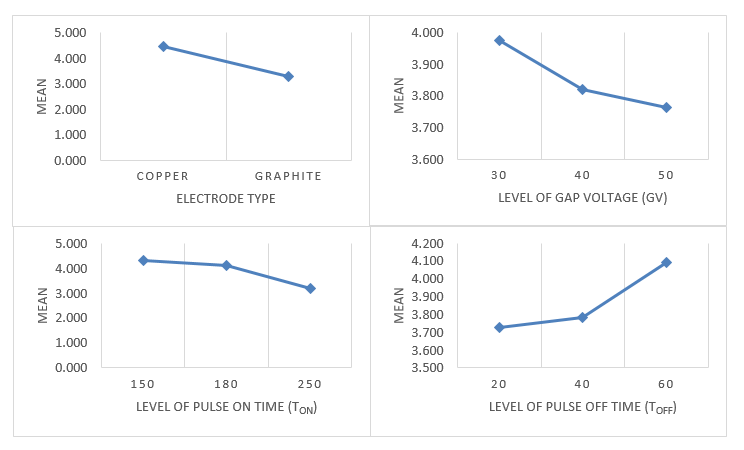
Fig. 3 Response Graphs for the Mean Values of Surface Roughness (SR)

4.2 BPNN Result

The values of the response variables including MRR and SR were predicted using BPNN. For training, testing, and validation, the data collected for each output response were divided randomly. A trial-and-error technique was used to obtain a BPNN architecture with the smallest MSE value. The following BPNN parameters were implemented in the trial-and-error method:

Based on the trial-and-error results, the minimum MSE value was obtained for an architecture with five hidden layers with five neurons in each hidden layer, as shown in Figure 4.

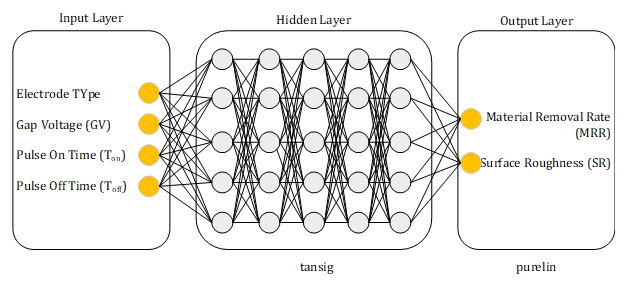
Fig. 4 BPNN Network Architecture

The activation function used for each hidden layer was tansig and for the output layer purelin. The value of MSE for MRR and SR was 9.837e^-05 and 1.042e^-04, successively. Figures 5 and 6 represent a comparison graph between BPNN prediction results and experiment data, whereas Table 4 displays the distributed data for training, testing, and validation, including the error values between predictions and experiments. MRR and SR achieved an average BPNN prediction error value of 0.303% and 0.43%, successively. Each response's average error value was less than 5%, proving that BPNN had accurately predicted all of the output responses[34].

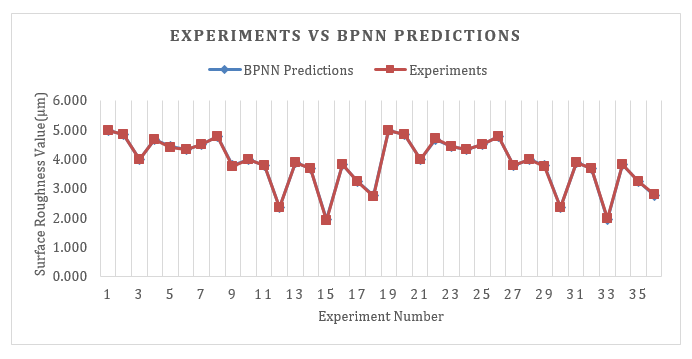
Fig. 5 Comparison Graph Between BPNN and Target Predictive Results for Surface Roughness

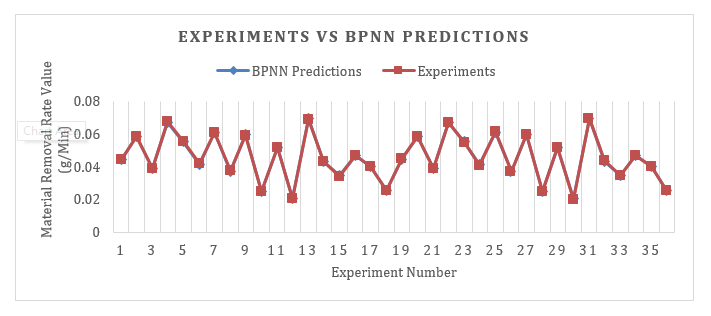
Fig. 6 Comparison Graph Between BPNN and Target Predictive Results Material Removal Rate

Table 4 Comparison of Experimental Results with BPNN Predictions

Note: Bp = BPNN prediction result, Er = Experiment Result, Tr = Training, Ts = Testing, Val = Validation

Figures 7 and 8 show that the BPNN output or prediction results are in very good agreement with the experimental values, namely the correlation coefficient achieved for training, testing, validation, and all data for each response is close to 1. The results revealed a perfect correlation between the predicted and target values[35]. The selected architecture was then utilized as an optimization's objective function employing the GA techniques.

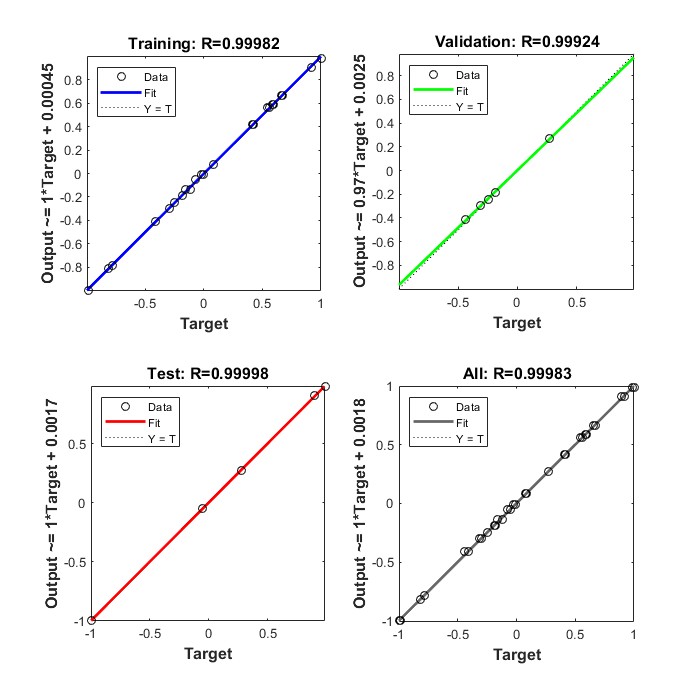
Fig. 7 Correlation Coefficient Graph for Training, Testing, Validation, and All Data for Material Removal Rate

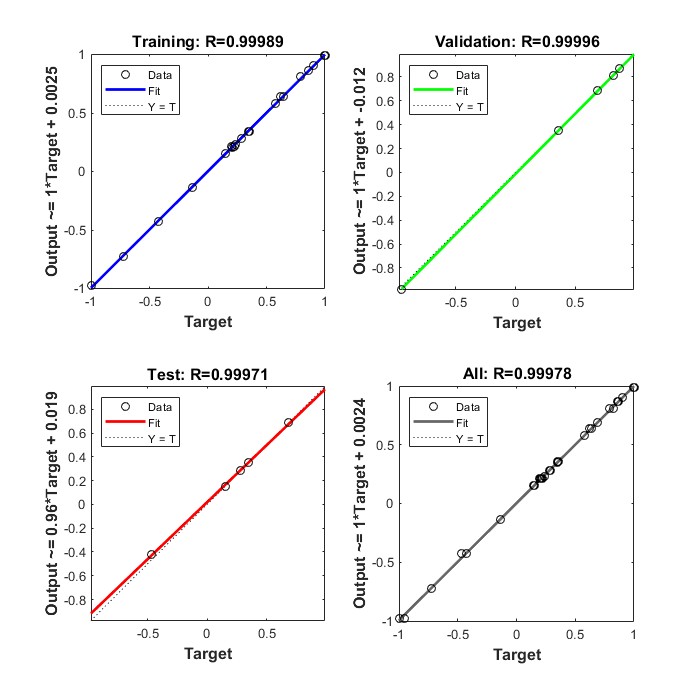
Fig. 8 Correlation Coefficient Graph for Training, Testing, Validation, and All Data for Surface Roughness

4.3 Fitness function

The fitness function was used to achieve optimum value. Fitness functions are determined based on their objective or modified functions. This research provided the fitness function based on the objective function generated by BPNN. The objective function produced from BPNN significantly affects the optimization results in the optimization process using the metaheuristic method. The smaller the MSE of the BPNN architecture used, the better the optimization results. The fitness function used for GA optimization is according to Formula 4. The equation was used to get the maximum fitness function.

[TeX:] \max{f(x)} = \text{Obj}_{1} - \text{Obj}_{2}$maxf(x)={\mathrm{\text{Obj}}}_1-{\mathrm{\text{Obj}}}_2$ (4)

where the objective function of MRR and SR are denoted by Obj₁ and Obj₂, respectively.

4.4 Genetic Algorithm result

The GA parameters employed during the optimization are as follows:

Table 5 contains the GA optimization values for corresponding EDM process variables. The BPNN prediction results based on these EDM process variables achieved successive results for MRR and SR at 0.0750 g/min and 1.914 μm, respectively. Figure 9 illustrates the GA iteration graph, which shows that the iteration began to converge on the 140th iteration with an optimization time of 1788.84 seconds. Furthermore, it can be seen from Table 5 that the SR reduced and the MRR improved with the optimized variables. Implementing the GA resulted in a 7.65% increase in MRR and a 50.72% reduction in SR. The optimized variable increased productivity with high MRR and workpiece surface quality in terms of low SR values compared to experimental process variables. Consequently, it can be confirmed that the proposed technique provides the most effective method to increase the performance of the EDM process.

Table 5 Genetic Algorithm Optimization Result

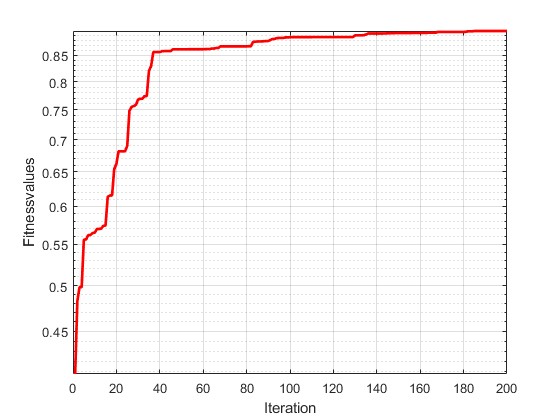
Fig. 9 Iteration Graph GA

5. Conclusion

In this research, the EDM sinking variable optimization process was performed on the AISI P20 and produced optimal responses (maximum MRR and minimum SR) using BPNN as modelling and GA as optimization technique. The conclusions of this study are as follows: