1. Introduction
There are numerous studies on mixed lubrication in slider bearings that take into account the effect of surface roughness[1-8]. They assume the lubricating film in the whole bearing is a continuum despite the film thickness value. This is obviously inadequate when the lubricating film thickness is so low that the effect of adsorbed layer is included[9]. The performance of the hydrodynamic slider bearing in this regime considering the surface roughness has not been investigated before.
Classical theories for hydrodynamic thrust bearings assume rigid bearing surfaces as the surface elastic deformation resulting from low film pressures (often no more than 10MPa) to be far smaller than the bearing clearance[10-12]. However, when the film thickness is decreased to the same scale as the adsorbed layer thickness, even in normal operating conditions the surface elastic deformation resulting from hydrodynamic pressures is surely comparable to the bearing clearance. In this case, the surface elastic deformation must also be considered. There are many studies on hydrodynamic thrust bearings which take into account surface elasticity[13-17]. However, those researchers assumed the continuum film in the whole bearing which is inadequate for low bearing clearances.
This study analyses the mixed elastohydrodynamic lubrication in the step bearing considering the effect of adsorbed layer. In this bearing, there is a previously described sandwich film. The studied hydrodynamics is thus complicated and multiscale. The problem is highly non-linear, and the numerical approach is thus required (by finite difference method). The study is new and important for recognizing the operation of the step bearing in mixed lubrication.
2. Lubrication Status
The investigated step bearing is shown in Figure 1. It survives the sandwich film due to the low lubricating film thickness. The surface roughness is sinusoidal and present on the static surface. The lower surface moves at the speed u; It is assumed to be ideally polished. hbf is the thickness of the adhering layer; h is the thickness of the intermediate film; is the surface gap at the inlet; is the surface gap at the outlet. Rz is the surface roughness magnitude. l1 and l2 are the widths of the two sub-zones, respectively. ∆h is the step size.

Fig. 1 Lubrication status instudied bearing
3. Mathematical Analysis
In this bearing, only some lubricant molecules can be adsorbed on the solid surface in the normal direction. Due to the lubricant-surface interaction potential, the discontinuity in the adhering layer is varied, which causes both the variation of the local density and the variation of the local viscosity. The flow of the adsorbed layer is essentially molecular in nature. The intermediate fluid flow is macroscopic and is essentially part of the continuum. Here, the equations of Zhang[9] are used to model the flows of the adhering layer and the intermediate fluid.
This analysis assumes that:
(a) The two surface materials are the same;
(b) the fluid rheology follows the Newton's law;
(c) No side flow occurs;
(d) No slip occurs at the interfaces;
(e) The viscous heating of the liquid film is negligible.
There are discrete points in the bearing, as shown in Figure 1. The coordinate of each point is: , where and J is the order number.
The basic mathematical equation for the flow is[9]:
(1)
where qm is mass flow rate, , p is film pressure, is lubricant density, is lubricant viscosity, is adhering layer density, is adhering layer viscosity, D is fluid molecule diameter, ∆x is the molecular separation in the flow direction in the adhering layer, qo is average value of , is separation between the (j+1)th and jth molecules in a normal adhering layer to the solid surface), , , , is the number of fluid molecule in the adhering layer thickness, -molecule separation in the adhering layer thickness on the adhering layer-fluid boundary. The formulations of I, II, Ѱ and Φ are shown in Ref.[9]. It is presumed that , where Υ is constant and is the local viscosity between the jth and (j-1)th molecules in the adhering layer thickness.
The lubricant bulk viscosity is:, where and - lubricant atmospheric viscosity. The lubricant density is: , where -constant and -lubricant bulk atmospheric density.
Equation (1) is rewritten as:
(2)
where:
(3)
(4)
It is formulated that:
(5)
(6)
By forward difference, it is obtained that:
, for J=1, 2, 3…, 2N (7)
This leads to:
, for J=1, 2, 3, …, 2N (8)
Because , combining Eqs. (7) and (8) yields:
for J=1, 2, 3, …, 2N (9)
The bearing load is:
(10)
4. Calculation Method
4.1 Numerical Calculation of Surface Elastic Deformation
The integration in Eq. (5), as shown below, cannot be calculated precisely owing to the unknown function for the film pressure:
(11)
Here, by putting the film pressures in the sectional area [, ] as , it is numerically obtained that:
(12)
where:
(13)
It is integrated from Eq. (13) that:
(14)
4.2 Numerical Approach
TheMATLAB calculation software was programmed and the used numerical procedure we used is shown in Figure 2. Rigid surface: is the pressure, is the lubricating film thickness, is the bearing load, is the lubricating film thickness at the bearing outlet. Elastic surface: is bearing load for , is bearing load for . k is the ordinal number of the iterative calculation. , and are the values of , p and htot in the kth iterative calculation. is the relaxation factor.
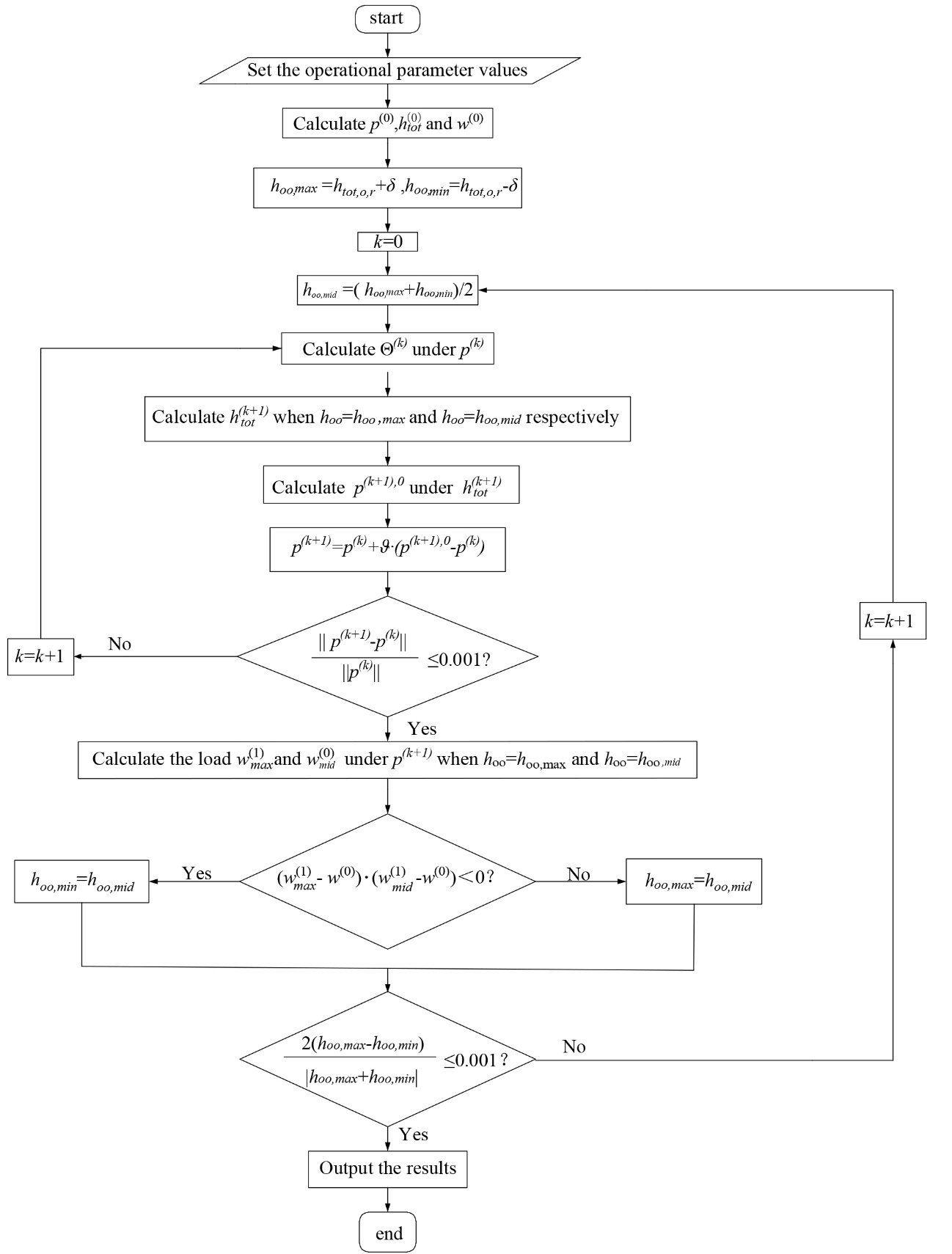
Fig. 2 Numerical program flow chart
4.3 Input parametric values
It was assumed that:
N = 3000, , , , , , , , , δ = 5nm ,
,
It is formulated that and . The formulations of Cy and Cq are given in Ref.[18]. Reference[9] shows the formulations of F1, F2 and ε. The weak, medium and strong lubricant-surface interactions were considered. The corresponding parameter values for these interactions are given in Ref.[19]. Different bearing surface materials were used. Table 1 shows the corresponding physical quantities.
Table 1 Physical quantities for different materials
5. Numerical Calculation Results
According to the above numerical calculation method and the input operational parameter values, the obtained numerical calculation results are discussed as follows.
5.1 Effect of the Surface Elastic Deformation
Figures 3(a)-(c) compare the film pressure distributions respectively for rigid surfaces and the elastic steel bearing surfaces for w=288 N/m and Rz=3 nm. The surface elastic deformation significantly reduces the maximum pressure and changes the film pressure distribution very clearly. For a given load, the effect of surface elastic deformation on the hydrodynamic pressure appears hardly relevant to the adsorption strength of the adhering layer. If the bearing is rigid or elastic, the surface roughness leads to significant pressure ripples. In Figures 4(a)-(c), the surface separation distributions are compared respectively for rigid surfaces and the elastic steel bearing surfaces for different adsorption strengths of the adhering layer for w=288 N/m and Rz =3 nm. (Under the same load) the bearing elastic deformation decreases both for the smallest bearing clearance and for the total lubricating film thicknesses. Also, for a given load, the effect of bearing elastic deformation on the lubricating film thickness is hardly dependent on the physical adsorption strength of the adhering layer.
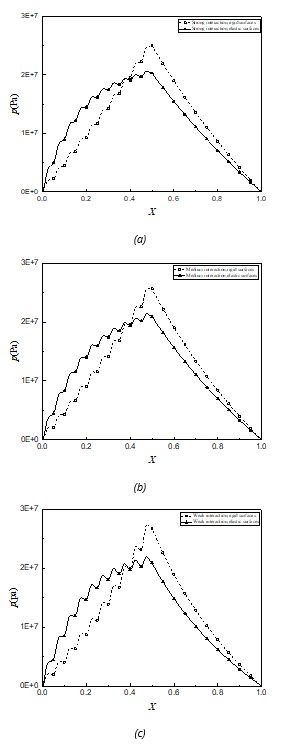
Fig. 3 Comparisons between film pressure distributions for rigid surfaces and elastic steel bearing surfaces when w=288 N/m and Rz=3 nm
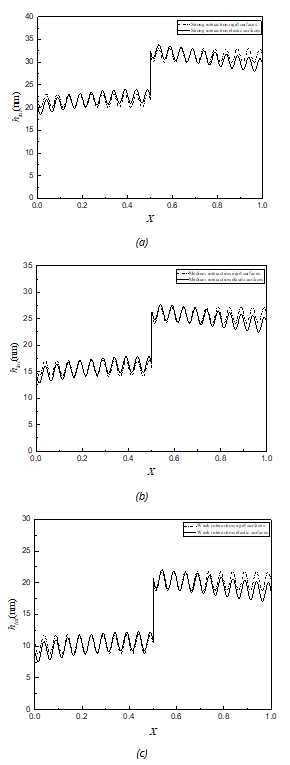
Fig. 4 Comparisons between surface separation profiles for rigid surfaces and elastic steel bearing surfaces for different adsorption strengths of the adsorbed layer when w=288 N/m and Rz=3 nm
Figures 5(a)-(c) compare the film pressure distributions for rigid surfaces and elastic steel bearing surfaces for different surface roughnesses at =19 nm, and weak, medium and strong adsorption strength. can be seen that for a given value of , the film pressures are significantly increased by the surface roughness if the surfaces are rigid or in elastic deformation. However, when the elastic deformations of the steel surfaces are considered, the influence of the surface protrusion on the hydrodynamic pressure is weakened, and hydrodynamic pressure waviness is significantly weakened at a relatively high surface protrusion. When is given, the surface elastic deformation reduces the maximum pressure more and changes the pressure distribution when the adsorption strength is higher. If the bearing surfaces are elastic, the effect of the adsorption strength on the pressure is weaker than with rigid surfaces.
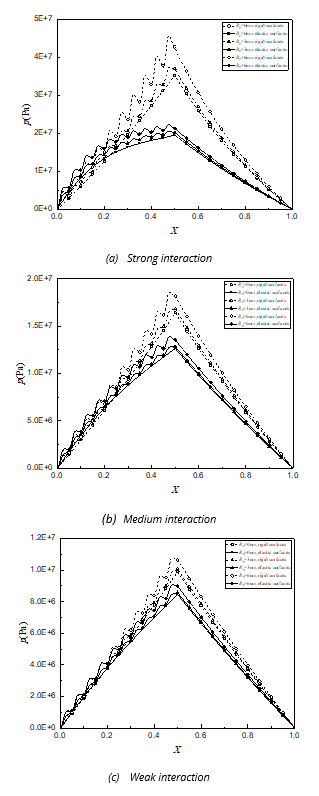
Fig. 5 Comparisons between hydrodynamic pressure distributions for rigid surfaces and for elastic steel bearing surfaces for different surface roughness when =19 nm
5.2 Influence of Bearing Elasticity on the Load
In Figure 6, the bearing load is increased by the surface roughness for =19 nm, where by the gradient of the load with surface roughness is smaller for the elastically deformed steel bearing surfaces than for rigid surfaces, especially with the strong physical adsorption of the adhering layer. With elastically deformed bearing surfaces, the effect of physical adsorption on the load is weaker than with rigid surfaces. For given values of and Rz, the bearing surface elastic deformation reduces the bearing load considerably, especially with strong physical adsorption and greater surface roughness.
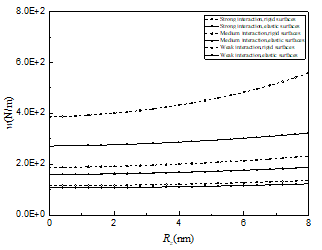
Fig. 6 Variations of bearing load with surface roughness for rigid surfaces and elastic steel bearing surfaces for different physical adsorptions when =19 nm
5.3. Bearing Performance with Different Materials
Figure 7 indicates that for a given load and surface roughness, the pressure profiles quite differ for different bearing materials. For carbonized silicon, which has the largest Young’s modulus of elasticity, the film pressure profile is close to that for rigid surfaces. For non-crystalline silica, which has high elasticity, the hydrodynamic pressure profile flattens with a reduction of maximum film pressure. The lower the elastic modulus of the surface, the lower the maximum pressure, and the greater the deviation of the pressure distribution from that of rigid surfaces, the more flattens the film pressure.
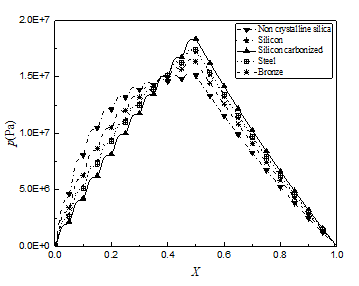
Fig. 7 Film pressure distributions for different bearing materials for the medium-level physical adsorption when w=187.2 N/m and Rz=3 nm
Figure 8 shows that that for a given load and surface roughness, the bearing material has a significant influence on the surface separation profile due to the elastic deformation of the bearing. The lower the modulus of elasticity of the bearing, the smaller the minimum surface separation and total surface separation. For non-crystalline silica, the minimum bearing clearance is significantly lower and the surface separation profile differs significantly from that for rigid surfaces.
Figure 9 shows the w versus curves for different bearing materials when the bearing elastic deformation is considered. These curve slopes represent the film stiffness. For a given operating condition, when the elastic modulus of the bearing is lower, the film stiffness becomes smaller. The film stiffness for carbonized silicon is obviously greater than that for non-crystalline silica, especially at lower values of .
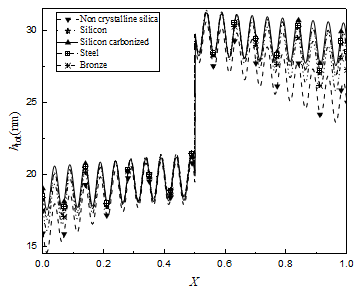
Fig. 8 Comparisons of the lubricating film thickness distributions for different bearing materials for the medium-level physical adsorption when w=187.2 N/m and Rz=3 nm
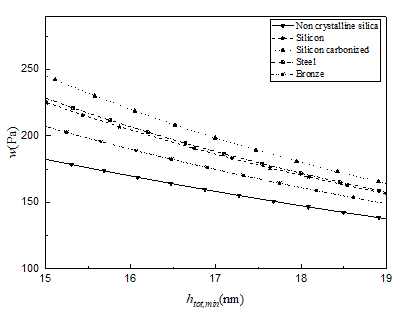
Fig. 9 The w versus curves for different bearing materials for the medium-level physical adsorption when Rz=3 nm
6. Conclusions
Mixed lubrication is investigated theoretically in the step bearing, considering the influences of the adhering layer, the surface protrusion and the bearing elastic deformation. Both the adhering layer and the intermediate fluid are present throughout the bearing. In this bearing, the sandwich film flow should be modeled mathematically correctly.
The numerical calculations were performed, and it was found that:
The effect of surface roughness is weaker for elastically deformed surfaces than for rigid surfaces. For a given operating condition, a bearing surface with a low Young’s modulus greatly reduces the maximum pressure and minimum bearing clearance, greatly changes both the film pressure profile and the lubricating film thickness distribution, and significantly reduces the film stiffness.
If the elasticity of the steel bearing is taken into account, both the film pressures and load increase less due to the surface roughness when compared to rigid surfaces, especially for strong physical adsorption. It is more evident for the bearing with a low elastic modulus.
If the bearing surfaces are rigid or elastic, surface roughness leads to the film pressure ripples. If the surface roughness is a relatively high, the surface elastic deformation considerably reduces the waviness of the pressure film.
When modelling the mixed lubrication in a thrust bearing with very small clearances, factors of adhering layer, surface roughness and surface elastic deformation ought to be considered, since the sizes of these three elements are all comparable to the bearing clearance.
