Skoči na glavni sadržaj

Nafta i Plin, Vol. 39. No. 158., 2019.

Stručni rad

Određivanje rasporeda veličine pora uz pretpostavku različitih pornih geometrija

Domagoj Vulin ; RGN Fakultet Sveučilišta u Zagrebu
Filip Vodopić ; RGN Fakultet Sveučilišta u Zagrebu
Marko Gaćina ; INA d.d.

Puni tekst: hrvatski pdf 11.922 Kb

str. 60-77

preuzimanja: 621

citiraj

Preuzmi JATS datoteku

Sažetak

Opisane su metode mjerenja kapilarnih tlakova te fizikalna povezanost kapilarnih tlakova, tj. močivosti i geometrije pora. Predstavljeni su različiti geometrijski modeli kojima se može predstaviti porni prostor uzorka stijene te su izračunate i uspoređene raspodjele veličina pora uz različite pretpostavke njihove geometrije. Ustanovljeno je kako pri najmanjim radijusima pora, odabir geometrije ne utječe bitno na procjenu njihove zastupljenosti, međutim kod većih pora pretpostavka geometrije pora može bitno promijeniti procjenu raspodjele veličina pora. Korištene su dvije različite metode računanja: metoda temeljena na procjenama radijusa zakrivljenosti meniskusa u kapilari i MSP-OBA metoda koja koristi omjer površine pora i njihovog opsega. Kako se zakrivljenost pore približava obliku kružnica, raspodjela će davati sve veće vrijednosti ekvivalentnog polumjera pora zbog smanjenja utjecaja zaostajanja močive faze u kutevima pora. Naposljetku, napravljena je i statistička analiza raspodjele veličine pora.

Ključne riječi

kapilarni tlak; močivost; raspodjela veličine pora; polumjer pora; geometrija pora; G faktor

Hrčak ID:

222606

URI

https://hrcak.srce.hr/222606

Datum izdavanja:

15.7.2019.

Posjeta: 1.486 *

Publication date: 15 July 2019

Volume: 39

Issue: 158

Pages: 60-77

DOI:

Article Information (continued)

Categories:

Subject: Stručni rad

Categories:

Subject: Professional Paper

Keywords:

Keyword: East-Med plinovod

Keyword: Levantska regija

Keyword: energetska geopolitika

Keyword: sigurnost opskrbe i energetska neovisnost

Keyword: geopolitički i geostrateški izazovi

Keyword: gravitirajuća regija

Keywords:

Keyword: East-Med gas pipline

Keyword: Levant region

Keyword: energy geopolitics

Keyword: security of supply and energy independence

Keyword: geopolitics and geostrategic challenges

Određivanje rasporeda veličine pora uz pretpostavku različitih pornih geometrija

Translated Title (en): Calculating pore size distribution with an assumption of different pore geometries

[ORCID] Vulin Domagoj[1]

Email: domagoj.vulin@rgn.hr

 

RGN Fakultet Sveučilišta u Zagrebu Faculty of Mining, Geology and Petroleum Engineering University of Zagreb Pierottijeva ul. 6, 10000, Zagreb

[ORCID] Domagoj Vulin[1]

Email: domagoj.vulin@rgn.hr

 

RGN Fakultet Sveučilišta u Zagrebu Faculty of Mining, Geology and Petroleum Engineering University of Zagreb Pierottijeva ul. 6, 10000, Zagreb

[ORCID] Filip Vodopić[2]

Email:

 

RGN Fakultet Sveučilišta u Zagrebu Faculty of Mining, Geology and Petroleum Engineering University of Zagreb Pierottijeva ul. 6, 10000, Zagreb

[ORCID] Marko Gaćina[3]

Email: marko.gacina@ina.hr

 

INA d.d. INA Inc. Avenija Većeslava Holjevca 10, 10000 Zagreb

Author notes:

Correspondence to: [*] Domagoj Vulin, RGN F, Pierottijeva ul. 6, 10000, Zagreb domagoj.vulin@rgn.hr

Abstract

Opisane su metode mjerenja kapilarnih tlakova te fizikalna povezanost kapilarnih tlakova, tj. močivosti i geometrije pora. Predstavljeni su različiti geometrijski modeli kojima se može predstaviti porni prostor uzorka stijene te su izračunate i uspoređene raspodjele veličina pora uz različite pretpostavke njihove geometrije. Ustanovljeno je kako pri najmanjim radijusima pora, odabir geometrije ne utječe bitno na procjenu njihove zastupljenosti, međutim kod većih pora pretpostavka geometrije pora može bitno promijeniti procjenu raspodjele veličina pora. Korištene su dvije različite metode računanja: metoda temeljena na procjenama radijusa zakrivljenosti meniskusa u kapilari i MSP-OBA metoda koja koristi omjer površine pora i njihovog opsega. Kako se zakrivljenost pore približava obliku kružnica, raspodjela će davati sve veće vrijednosti ekvivalentnog polumjera pora zbog smanjenja utjecaja zaostajanja močive faze u kutevima pora. Naposljetku, napravljena je i statistička analiza raspodjele veličine pora.

Translated Abstract

Methods for measuring capillary pressures are presented along with the correlation between capillary pressure, wetability and pore geometry. Different pore geometries are presented which can describe pore network of a rock sample. Furhermore, pore size distributions for each geometry are calculated. It is determined that pore geometry for small radius pores have a small impact on pore size distribution. However, pore geometry for larger pores can have a great impact on pore size distribution. Two different methods are used for calculating pore size distribution: method based on radii of curvature of interface in a capillary tube and MSP-OBA method which uses ratio of pore area and their respective perimeter. As the number of sides of polygonal geometries increases, pore size distribution will result in greater equivalent pore radii because of decreasing wetting phase retention in the pore corners. Finally, statistical analysis of pore size distribution is implemented.

Uvod

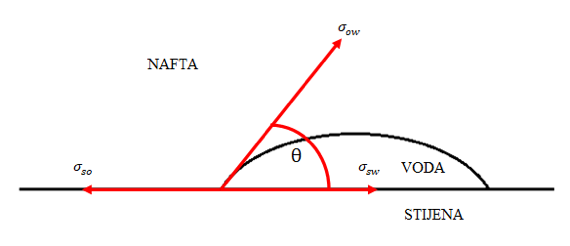
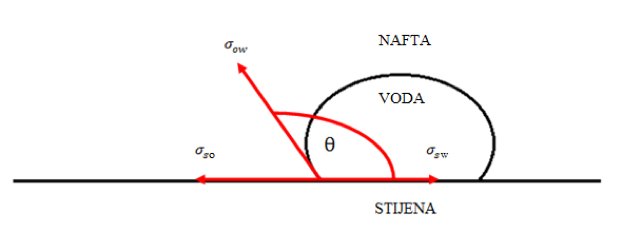
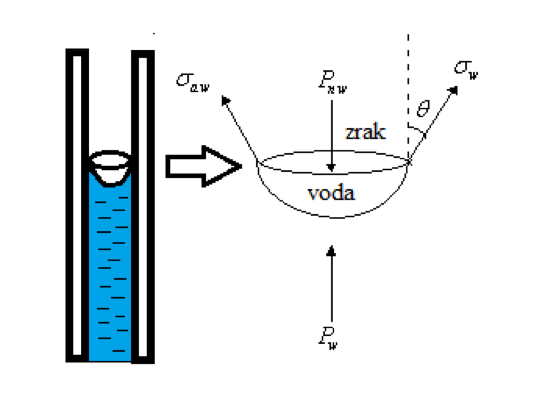
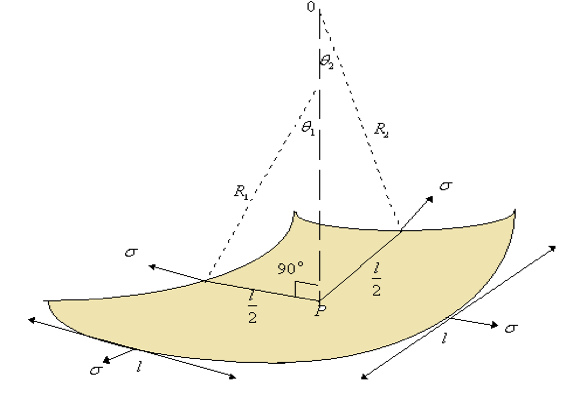
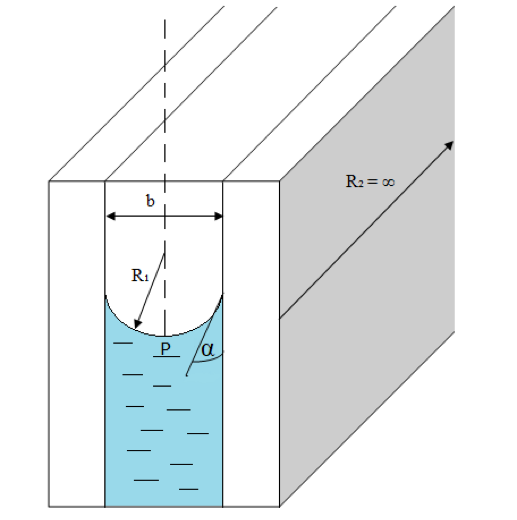
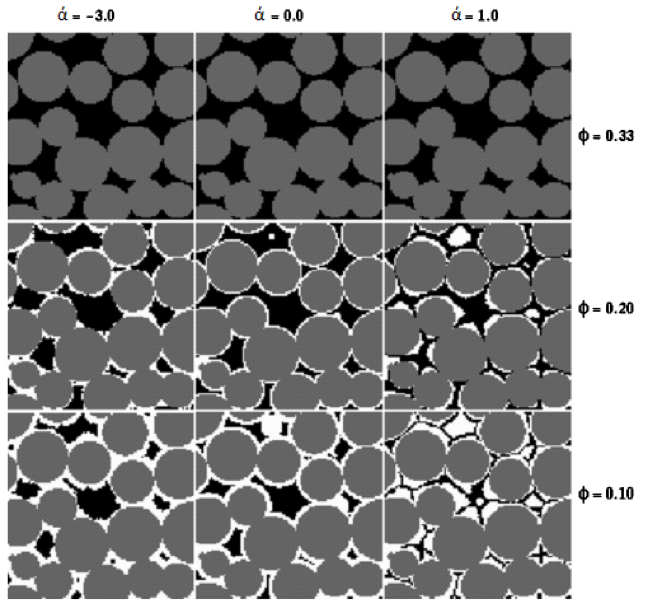
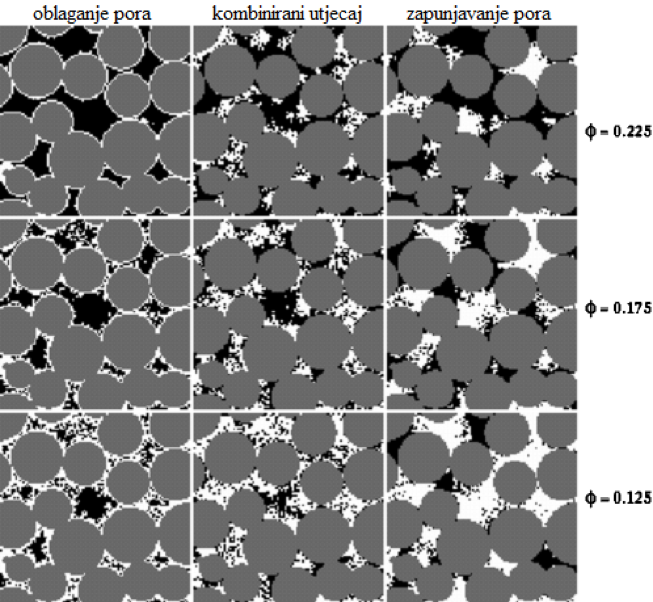
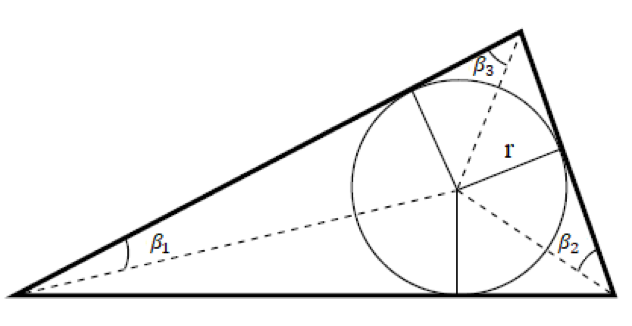
Raspored veličina pora ima značajnu ulogu pri određivanju zasićenja vodom iznad kontakta, odnosno razdjelnice nafta-voda te pri određivanju kapilarne blokade protoka. Također, utječe i na efektivnu propusnost poroznog medija, tj. na krivulju kapilarnog tlaka u ovisnosti o zasićenju fluidima. Kako se raspored veličine pora može odrediti iz prethodno spomenute analize, nužno je definirati pojavu kapilarnog tlaka. Kapilarni tlak je diferencijalni tlak koji se javlja na granicama faza (močive i nemočive) te je kao takav posljedica kapilarnih sila koje održavaju površinu granica faza u stanju ravnoteže, odnosno postiže se ravnotežno stanje (ekvilibrijum). Kapilarni se tlak javlja kao posljedica međupovršinske napetosti između faza koje su pak posljedica po intenzitetu nejednolikog međumolekularnog privlačenja između molekula koje se nalaze u unutrašnjosti fluida i molekula koje se nalaze na površini, tj. granici dvaju fluida. Međupovršinsku napetost predstavlja površinska sila koja djeluje u određenom smjeru na određenoj duljini: (1-1)
gdje je: σ - međupovršinska napetost [ Pa/m ] F - površinska sila [ N ] l - duljina na kojoj djeluje površinska sila [ m ] Intenzitet kapilarnog tlaka određuje i kontaktni kut (θ) između faza, koji se naziva kut močenja. U realnom slučaju, tj. u porama stijena mogu se nalaziti voda, nafta i/ili plin. Uzimajući za primjer slučaj da se u porama nalaze nafta i voda, razlikuju se vodomočive i naftomočive stijene. Veličina kuta močenja ovisio međupovršinskim napetostima, tj.o odnosu međupovršinskih sila stijena-nafta() i stijena-voda (). Slijedi: za onda je i stijena je vodomočiva(slika 1-1.), a ako je onda je i stijena je naftomočiva(slika 1-2.). U radu su uspoređene procjene raspodjele veličina pora uz pretpostavke različitih geometrija, čime se mijenjaju odnosi kontaktnog kuta i rezultantne močivosti, tj. sila adhezije na stijenu. Različite geometrije pora različito utječu na raspodjelu veličina, što je pokazano nakon statističke obrade te primjene različitih algoritama za procjenu veličina pora na temelju pretpostavljene distribucije te dominantne geometrije presjeka pornih kanala.

naftaiplin-60-77-g1.png naftaiplin-60-77-g2.png naftaiplin-60-77-g3.png naftaiplin-60-77-g4.png naftaiplin-60-77-g5.png naftaiplin-60-77-g6.png naftaiplin-60-77-g7.png naftaiplin-60-77-g8.png naftaiplin-60-77-g9.png naftaiplin-60-77-g10.png naftaiplin-60-77-g11.png naftaiplin-60-77-g12.png naftaiplin-60-77-g13.png naftaiplin-60-77-g14.png naftaiplin-60-77-g15.png

References

1 

AANONSEN, S.I.. Efficient history matching using a multiscale technique. (2005) In SPE reservoir simulation symposium. Society of Petroleum Engineers. . 2005.

2 

ALKHATIB, A. AND BABAEI, M.. Applying the Multi level Monte Carlo method for heterogeneity - induced uncertainty quantification of surfactant/polymer flooding. (2016) SPE Journal,. 21(04). 2016.

3 

ARCHER, R.A. Integration of Production Data Analysis Results into Geostatistical Models by Downscaling. (2007.) In Asia Pacific Oil and Gas Conference and Exhibition SPE. . 2007.

4 

HOTEIT, H. AND CHAWATHÉ, A.. Making Field-Scale Chemical Enhanced-Oil-Recovery Simulations a Practical Reality With Dynamic Gridding (2016.) SPE Journal. 21(06). 2016.

5 

HUNT, A., EWING, R., GHANBARIAN, B.. Percolation theory for flow in porous media (2014.) Springer. 880. 2014.

6 

JONOUD, S., WENNBERG, O.P., LARSEN, A. AND CASINI, G. Capturing the effect of fracture heterogeneity on multiphase flow during fluid injection (2013.) SPE Reservoir Evaluation and Engineering 16(02) 2013.

7 

MA, S., MASON, G., MORROW, N. R. Effect of contact angle on drainage and imbibition in regular polygonal tubes (1996.) Colloids and Surfaces A: Physicochemical and Engineering Aspects 117(03) 1996.

8 

MASON, G., MORROW, N. R. Capillary behavior of a perfectly wetting liquid in irregular triangular tubes (1991.) Journal of Colloid and Interface Science 14(1) 1991.

9 

MAYER, R.P. AND STOWE, R.A. Mercury Porosimetry-Breakthrough Pressure for Penetration Between Packed Spheres (1965.) J. Colloid and Interface Science 20, 893 1965.

10 

ØREN, P. E., BAKKE, S., ARNTZEN, O. J. Extending predictive capabilities to network models (1998.) SPE journal,  3(04), 324-336 1998.

11 

PIRI, M. Pore-scale modelling of three-phase flow. Centre for Petroleum Studies (2003.) Department of Earth Science and Engineering, Imperial College London. 2003.

12 

PRINCEN, H.M. Capillary Phenomena in Assemblies of Parallel Cylinders. I. Capillary Rise Between Two Cylinders () J. Colloid and Interface Science 30

13 

VALVATNE, P. H. Predictive pore-scale modelling of multiphase flow (Doctoral dissertation (2004.) Department of Earth Science and Engineering, Imperial College London). 2004.

14 

VULIN, D. Višefazni protok u poroznoj stijeni. (2019.) Interna skripta. Zagreb: RGN fakultet 2019.

15 

YOON, S., MALALLAH, A.H., DATTA-GUPTA, A., VASCO, D.W. AND BEHRENS, R.A. A multiscale approach to production-data integration using streamline models. (2001.) SPE Journal 6(02) 2001.

16 

Numbere, D.T. capillarypressure (2004.) University of Missouri-Rolla (4. 9. 2017.) 6(02) 2004. http://web.mst.edu/~numbere/cp/chapter%203.htm

This display is generated from NISO JATS XML with jats-html.xsl. The XSLT engine is libxslt.