APPLICATION OF THE SAP2000 COMPUTER PROGRAMME IN THE MODELLING OF AN UNDERGROUND QUARRY OF DIMENSION STONE

3.2. Input data

3.2.1. Geometry of the model

The default geometry of the model represents a quarter of the future excavation area, of which about a third is the excavation space and the rest is rock mass. Solid objects are used for the analysed model of the underground deposit of dimension stone. The model of the rock mass is divided into 5 different layers: the floor, the exploitation layer, the load-bearing lower layer of the immediate roof, the upper layer of the immediate roof and the layer of the upper roof, as shown in Figure 2.

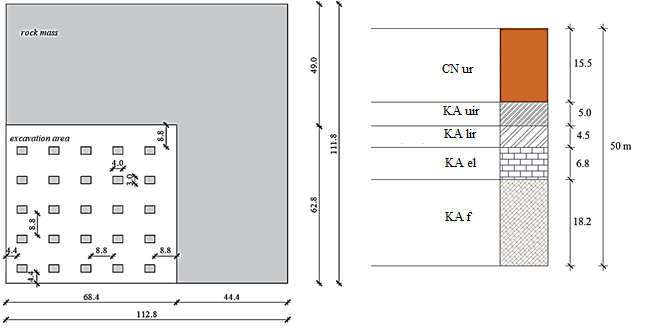
Figure 2: Geometry of the model: top plan at the quarter of the excavation area and layers of the rock mass.

3.2.2. Finite element mesh, assignment of loads and type of analysis

The possibility of phased modelling is used through “Stage construction analysis” in SAP2000. This enables a nonlinear static analysis in stages. Stage 1 represents the full rock mass model, stage 2 the post-exploitation model. Only the dead load of the layers is considered.

The model is divided into several smaller solid elements corresponding to the given geometry (see Figure 2), so that in the first stage it includes a full block with dimensions 112.8 m x 118.8 m, and in the second stage it includes an excavation according to Figure 2, as shown in Figure 3. The model contains 39,138 octagonal finite elements, and the total number of equilibrium equations is 121,176.

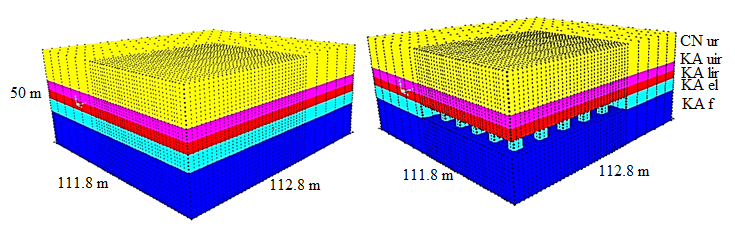
Figure 3: Finite element mesh of the model: a) Stage 1: the full block of the rock mass, b) Stage 2: the block after the exploitation.

3.2.3. Boundary conditions

At the bottom of the floor layer, the model is supported at all nodes in the x-, y- and z- directions, which prevents translational displacements and ensures the primary stability of the model. In the top view, over the entire height of the model, the boundary conditions are arranged according to Figure 4 due to symmetry, so that the model represents a quarter of the future exploitation field.

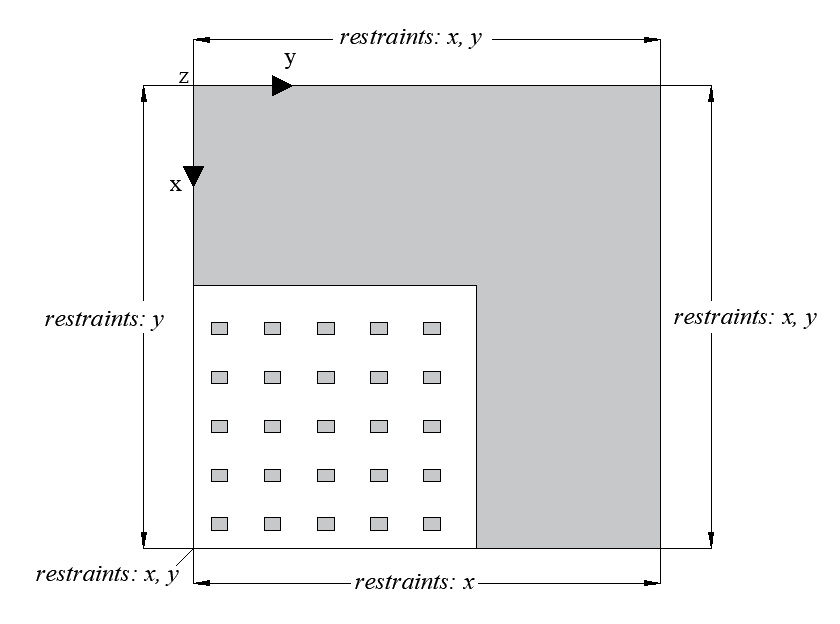
Figure 4: Floor plan view: boundary conditions

3.3. Results of numerical modelling

3.3.1. Stage 1: the full block model

For the complete block model (stage 1), the value of the primary vertical stresses in the central part of the exploitation layer is [TeX:] \sigma_{v} = 0.72\ MPa${\sigma }_v=0.72MPa$ (see Figure 5), which corresponds to the analytical stress calculation. The value ​​of primary horizontal stresses in the central part of the exploitation layer is [TeX:] \sigma_{h} = 0.39\ MPa${\sigma }_h=0.39MPa$.

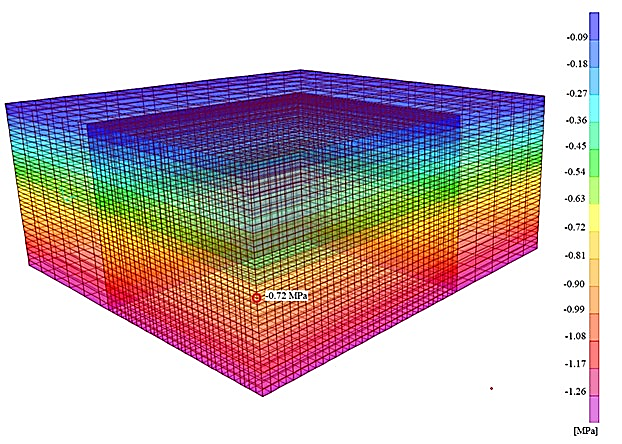
Figure 5: Stage 1: primary vertical stresses

The horizontal strains (x and y directions) are zero due to boundary conditions. The vertical strains (z-direction) are shown in Figure 6. The results are as expected: the values increase with depth, except for the layers of the immediate roof, since there the deformation modulus is much higher than in the upper roof layer (see Table 1).

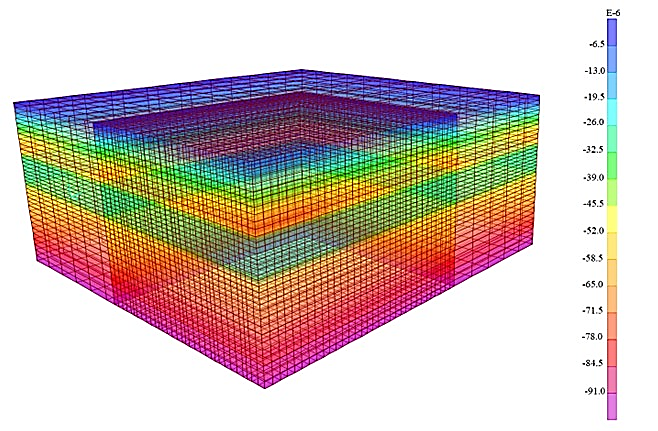
Figure 6: Stage 1: vertical strains

Figure 7 shows the vertical nodal displacements of the FEM mesh. The largest displacements are obtained at the top of the model and amount to 2.6 mm, whereas the displacements at the top of the exploitation layer (top of pillars) are 1.8 mm.

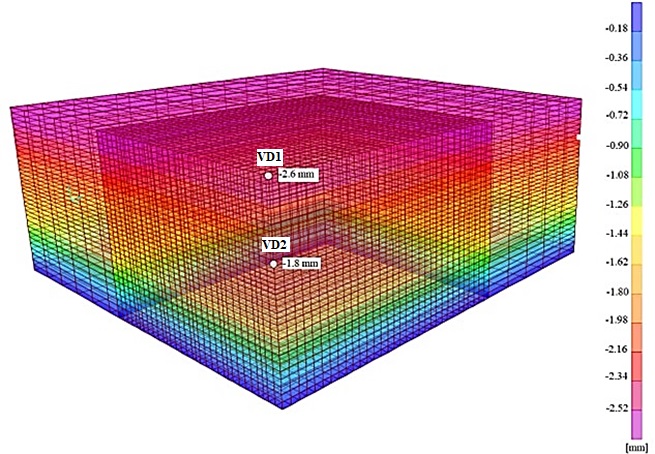
Figure 7: Stage 1: vertical displacements

3.3.2. Stage 2: post-exploitation model

For the post-exploitation model (stage 2), the highest values of vertical and horizontal stresses were obtained at the edges of pillars, [TeX:] \sigma_{v,\ max} = 12.22\ MPa${\sigma }_{v,max}=12.22MPa$ (see Figure 8) and [TeX:] \sigma_{h,\ max} = 4.52\ MPa${\sigma }_{h,max}=4.52MPa$.

The vertical stress at the centre of the most heavily loaded pillar is [TeX:] \sigma_{p} = 8.33\ MPa\ ${\sigma }_p=8.33MPa$(see Figure 8). The results of the vertical strains (z – direction) are in agreement with the previously determined stresses.

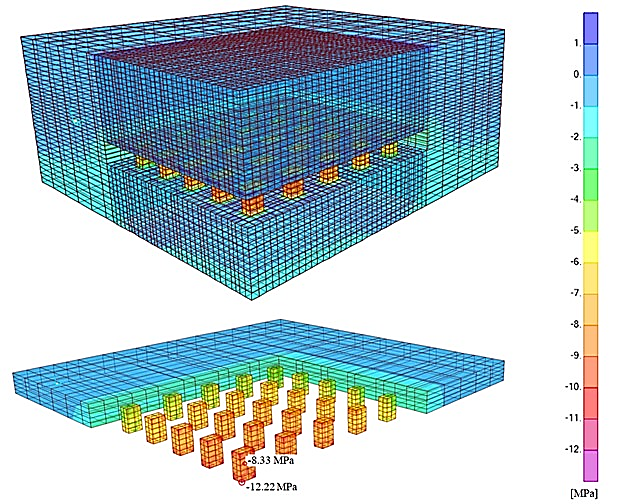
Figure 8: Stage 2: vertical stresses

​Figure 9 shows the vertical nodal displacements of the FEM mesh. To obtain the relative vertical displacements caused by excavation, the displacements of the stage 1 model must be subtracted from the total displacements. The obtained maximum value at the top of the model is 10 mm (relative value: 10 - 2.6 = 7.4 mm), and the maximum value at the top of the pillar is 9.1 mm (relative value: 9.1 - 1.8 = 7.3 mm). The vertical displacements at the top of the model at about 40 m from the excavation field correspond to the displacements of the complete block model (VD1 in Figures 7 and 9; 2.6 mm), as do the vertical displacements at the level of the top of pillars at about 25 m from the excavation field (VD2 in Figures 7 and 9; 1.8 mm).

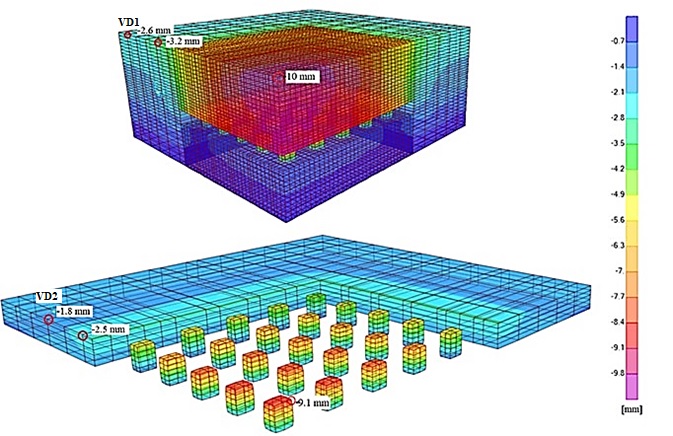
Figure 9: Stage 2: vertical displacements

4. Discussion

As far as controlling the results of numerical modelling is concerned, some revealing insights into the analysis of stresses can be obtained from simpler analytical solutions.

For a Poisson’s ratio of [TeX:] \upsilon = 0.35$\upsilon =0.35$ (see Table 1), the results for the full block model (section 3.3.1) confirm the relationship between the horizontal stresses [TeX:] \sigma_{h} = 0.39\ MPa${\sigma }_h=0.39MPa$ and the vertical stresses [TeX:] \sigma_{v} = 0.72\ MPa${\sigma }_v=0.72MPa$ according to the elasticity theory given in Equation 1 as follows:

[TeX:] \sigma_{h} = \frac{\upsilon}{1 - \upsilon}\sigma_{v}\text{\ \ \ \ \ }${\sigma }_h=\frac{\upsilon }{1-\upsilon }{\sigma }_v$ (1)

For the post-exploitation model (stage 2), the strength factor of the point with the highest stresses, calculated as the ratio between the uniaxial compressive strength of the rock mass [TeX:] \text{UCS} = 27.055\ MPa$\mathrm{\text{UCS}}=27.055MPa$ (see Table 1) and the maximum vertical stresses [TeX:] \sigma_{v,\ max} = 12.22\ MPa${\sigma }_{v,max}=12.22MPa$ (Figure 8), is [TeX:] f_{s} = 2.21$f_s=2.21$, which fulfils the stability condition, Equation 2:

[TeX:] f_{s} = \frac{\text{UCS}}{\sigma_{v,\ max}}\text{\ \ \ \ \ }$f_s=\frac{\mathrm{\text{UCS}}}{{\sigma }_{v,max}}$ (2)

The tributary area method, based on elementary concepts of static equilibrium, provides a simple method for determining the average state of axial stress in pillars, which can then be compared to the average strength of the rock mass representative of the particular pillar geometry (Brady and Brown, 2005). This is particularly true for a sufficiently large number of rooms and pillars when mining an ore body of uniform thickness and a lower thickness of overburden compared to the width of the mining area.

According to the theory of the tributary area method, the analytical expression for calculating the average value of the vertical stresses in the pillar [TeX:] \sigma_{p}${\sigma }_p$ is:

[TeX:] \sigma_{p} = \sigma_{v}\text{\ \ }\frac{A_{t}}{A_{p}}\text{\ \ \ }${\sigma }_p={\sigma }_v\frac{A_t}{A_p}$ (3)

Where:

[TeX:] \sigma_{v}${\sigma }_v$ – primary vertical stresses in the rock mass (stage 1),

[TeX:] A_{t}$A_t$ – the corresponding total area of the pillar of the roof deposits,

[TeX:] A_{p}$A_p$ – cross-sectional area of the pillar.

According to Equation 3, the determined average value of vertical stresses in the pillar is [TeX:] \sigma_{p} = 9.06\ MPa${\sigma }_p=9.06MPa$, considering the primary stress state in the exploitation layers of 0.72 MPa (see Figure 5). This value is slightly higher than the value of 8.33 MPa in the centre of the most heavily loaded pillar obtained in the numerical analysis. However, it is appropriate to consider the implicit limitations of the tributary area method, which are mainly related to the neglect of the effects of the location of a pillar within an ore body or mining panel. The only appropriate solution can be obtained by the numerical analysis shown in Figure 8.

One of the main objectives of the numerical analysis was to determine the effect of underground excavation on the redistribution of stresses in the surrounding rock mass. Based on the solutions for vertical stresses (see Figure 8), a stress change of less than 10% was determined at a distance of 20 m from the underground excavation. The situation is, of course, quite similar for point displacements of the model (see Figure 9).

5. Conclusions

A numerical analysis of the part of the underground quarry of dimension stone with the designed maximum dimensions of the rooms was carried out to determine their stability and influence on the redistribution of stresses in the surrounding rock masses. The numerical analysis of the analysed model was performed with the SAP2000 software, which is intended for solving the stress and strain state of three-dimensional models applying the finite element method. SAP2000 is primarily used for the modelling of building constructions; however, in this paper the application of the programme in the field of mining was presented.

The obtained results confirmed the predicted behaviour of the rock mass. The highest concentrations of stresses and strains are found in the edge regions of the pillars, so their correct design is crucial. The analytically calculated average vertical stress in the pillar by the tributary area method is 9.06 MPa. Numerically, 8.33 MPa is obtained, and since this is the value ​​in the pillar with the highest stresses, it can be confirmed that the results of the analytical calculation are on the safe side.

The strength factor of the point with the highest stresses was determined analytically and a value of 2.21 was obtained, which fulfils the stability condition.

6. References

Kruk, B., Dedić, Ž., Kruk, LJ., Peh, Z., Kovačević-Galović, E. and Gabrić, A.: Rudarsko-geološka studija potencijala i gospodarenja mineralnim sirovinama Istarske županije (Mining-geological study of potential and management of raw materials in the Istarska County). Hrvatski geološki institut, Zagreb (in Croatian)

Sari, M. (2022): Two- and three-dimensional stability analysis of underground storage caverns in soft rock (Cappadocia, Turkey) by finite element method. Journal of Mountain Science, 19 (4), 1182-1202.

SAŽETAK

Primjena računalnoga programa SAP2000 u modeliranju podzemnoga kamenoloma arhitektonsko-građevnoga kamena

Numerička analiza dijela podzemnoga kamenoloma arhitektonsko-građevnoga kamena s projektiranim maksimalnim dimenzijama podzemnih prostorija provedena je pomoću softvera SAP2000, temeljenoga na metodi konačnih elemenata. Glavni cilj analize bio je ispitati stanje stabilnosti i utjecaj na preraspodjelu naprezanja u okolnim stijenskim masama i time potvrditi primjenu teorije tributary area. Analitičkom primjenom teorije tributary area dokazano je zadovoljavajuće slaganje s numeričkim proračunom, pri čemu su rezultati dobiveni analitičkim proračunom na strani sigurnosti. Dobiveni rezultati potvrdili su predviđeno ponašanje stijenske mase, što potvrđuje primjenu SAP2000 softvera u području rudarstva, iako se radi o softveru s uobičajenom primjenom u području građevinarstva. Najveće koncentracije naprezanja i deformacija nalaze se u rubnim dijelovima stupova, stoga je njihovo pravilno projektiranje ključno. Određen je faktor sigurnosti točke s najvećim naprezanjima i dobivena je vrijednost od 2,21, čime je zadovoljen uvjet stabilnosti. Što se tiče utjecaja na okolno područje, na temelju dobivenih vertikalnih naprezanja na udaljenosti od 20 m od podzemnoga iskopa utvrđene su promjene naprezanja manje od 10 %.

Ključne riječi: SAP2000, numeričko modeliranje, metoda konačnih elemenata, podzemni kamenolom, arhitektonsko-građevni kamen

Authors’ contribution

Tanja Mališ (1) (PhD, Assistant Professor, Civil Engineering) performed the numerical analysis and consolidated the paper. Petar Hrženjak (2) (PhD, Associate Professor, Mining Engineering) performed the field research and laboratory tests, provided interpretations and presentation of the analysis results. Antonia Jaguljnjak Lazarević (3) (PhD, Associate Professor, Civil Engineering) provided the interpretation of numerical and analytical calculation. Mislav Mikulec (4) (mag. ing. min, Mining Engineering) performed numerical and analytical calculation for a smaller corresponding model through their master thesis (Mikulec, 2020).