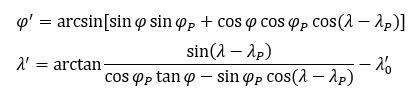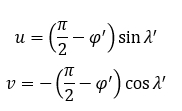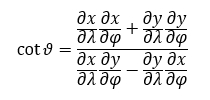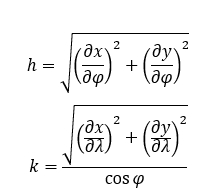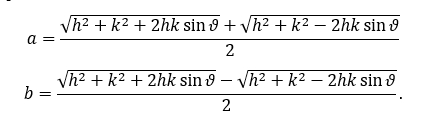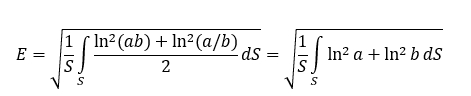A Low-Distortion Map of the World Ocean Without Discontinuities

1 Map projections of the World Ocean

Recent research on map projections sometimes tends to focus on continents rather than oceans. For example, the low-distortion maps ofCanters (2002) were all optimized for continents, and neglected distortions on oceans. While usual world maps do not have any significant data in oceans (e.g., political, agricultural, ethnographical maps), oceanographic research is also rising, producing data that concentrates on the hydrosphere of the Earth. Map projections for such themes should have their areas of low distortion in oceans. In this paper, the term World Ocean refers to the Pacific, Indian, and Atlantic Oceans altogether with all adjacent seas (i.e., not including the Caspian Sea).

First maps customized for the World Ocean as a single unit started to appear in the middle of the 20 ^th century. One may mention the Tetrahedric projection of Bartholomew from 1942 centred on the South Pole (Snyder 1993) as one of the first attempts to design a map of the World Ocean. However, this early map had severe discontinuities in the Pacific Ocean, and displayed the Arctic Ocean cut in three pieces.

Probably most mappings for the World Ocean were designed by Spilhaus. His maps were developed using two different basic ideas. His earlier projections applied former known mappings, like the Hammer, August or Adams projections in oblique transverse or plagal aspects (Spilhaus 1942,1983,Wray 1974). The apparent goals in selecting the aspect parameters were not only reducing the distortion in the oceans, but also to depict the World Ocean as a single, continuous unit. However, Spilhaus could not achieve the second goal completely. His projections interrupt the World Ocean not only across the Bering Strait (which may be an acceptable trade-off), but significant portions of the Caribbean Sea are also cut in his maps. Depending on the exact design, other discontinuities near the shorelines of the Pacific Ocean or in the South China Sea are also observable.

The reason of this is that common map projections have a cut at longitude 180°. For maps of land, this is not a big problem, as centring the map on longitude 10°E, this discontinuity is moved to meridian 170°W, cutting only a few tiny islands near the Bering Strait. However, this discontinuity runs along a half of a great circle, which holds even for maps in rotated aspects. On the other hand, the World Ocean has such a great extent, that it is impossible to place a half of a great circle so that it would not cross any large water body. Thus, only a more sophisticated map projection with less discontinuity could solve the continuous representation in plagal aspect.

Some later maps ofSpilhaus (1983) followed another path. He interrupted the Earth along complicated geographical lines (mostly along shorelines of oceans) and built compound map projections displaying different parts of the Earth in varying mappings. The reader may find details of this concept and a more elabo-rated history of oceanic maps in another co-authored paper of the author (Cameron and Kerkovits 2022).

An obvious advantage of the latter approach is that the more discontinuities we allow the more the distortions can be reduced. Placing discontinuities along natural boundaries may allow certain map themes to be plotted without discontinuities. A projection was developed using this method recently byCameron and Kerkovits (2022).

A disadvantage of this method is that the description of the discontinuities requires complicated, irregular lines, which can only be stored in GIS as complex polylines approximating the theoretical boundaries. Furthermore, sometimes even discontinuities along lands might be undesired by the mapmaker. Therefore, this paper presents another concept of creating an oceanic view of the Earth with the least possible discontinuities.

2 Design Principles

As stated previously, a map projection with discontinuity along meridian 180° is not sufficient for a map of the World Ocean, so the mapping is designed to have almost no places of discontinuity. However, while the Earth has a closed surface, the map plane is an open surface. Thus, it is not possible to construct a homotopy (continuous mapping) between them. Removing a single point from the surface of the Earth results in an open surface, making the homotopy onto the plane possible. So, one may conclude that it is necessary and sufficient to interrupt the surface of the Earth at a single point to create a map projection on the plane.Spilhaus (1983) did discuss this possibility, and recommended to move the discontinuity to 45°N 85°E.

At this point, it is necessary to define the shape of the Earth. For the sake of simplicity, it will be approximated by a unit sphere. The ~20 km difference between the sphere and the actual shape of the Earth can be safely neglected in small-scale maps.

Among previously known map projections, azimuthal, pseudoazimuthal, and polyazimuthal projections have a discontinuity only at the South Pole, which can be moved to any arbitrary point in plagal aspect. However, azimuthal and pseudoazimuthal projections have severe distortions in the outer hemisphere, so they are unacceptable candidates for a world map. Polyazimuthal mappings are complicated and obscure, their usefulness for world maps has not been investigated by anyone yet. Choosing only a single point of discontinuity, it is inevitable that distortions will rise compared to traditional world maps (as a side-effect of having less discontinuity), so they must be constrained by advanced methods: A tailor-made projection must be developed using numerical optimization.

Projections having a discontinuity at a single point will always have infinite linear scale along the metaparallel at that point. It is easy to see: this point is mapped to the boundary of the map (a closed curve), so this infinitely small point gets stretched to a finite line. Therefore, this point should be moved as far from the area of interest as possible to optimize distortion. This is most conveniently done by the metagraticule system introduced byWray (1974). Assuming that the point of discontinuity is at the South Pole, the graticule is rotated in the space. The rotated counterparts of the graticule lines are denoted by the prefix meta-. Applying the formulae of the projection for metalatitudes and metalongitudes instead of latitude and longitude, the discontinuity will be moved to the freely chosen South metapole. If the angles of rotation are not multiples of the right angle, the map projection is said to be in plagal aspect.

Optimization of map projections was discussed in detail byCanters (2002). He stated that existing projections may be arbitrarily modified using polynomial transformations. Polynomials may approximate any smooth function, so it may also be a reasonable approximation of the best possible map projection. However, the initial projection must be chosen carefully: polynomials may only approximate smooth mappings, so they never introduce or cancel discontinuities, and cannot cancel infinite distortions of the initial map. For example, if the stereographic projection were chosen as the initial projection, the South metapole will be infinitely far in the map regardless of the polynomial. On the other hand, the Lambert azimuthal equal-area projection has linear scale of zero in the direction of metameridians at the South metapole (it compresses map content in the meridian direction infinitely). This may also not be changed by any polynomial transformation. It is reasonable to assume that such infinite distortions are not present in the optimal projection (in this paper, the term optimal refers to the map projection that has the lowest distortion possible according to some distortion criterion; this has no implication on its practical usefulness at all), so a simple candidate for the initial projection is the azimuthal equidistant one.

3 Mathematical Basis

As this projection will be used in plagal aspect, one should use the metalatitude φ' and metalongitude λ' instead of latitude φ and longitude λ (Snyder 1987,Lapaine and Frančula 2016):

Here, the coordinates φ _P and λ _P of the metapole (which appoint a centre for the main topic of the map, that is the World Ocean) and the azimuth λ' ₀ of the prime metameridian may be subject of optimization.

In the next step, the azimuthal equidistant projection (Snyder 1987) is applied for the metacoordinates (planar coordinates for this intermediate plane are denoted by u and v):

Finally, this map is transformed by a fifth-degree polynomial transformation:

x = a ₁₀ u + a ₃₀ u ³ + a ₁₂ uv ² + a ₅₀ u ⁵ + a ₃₂ u ³ v ² + a ₁₄ uv ⁴

y = b ₀₁ v + b ₂₁ u ² v + b ₀₃ v ³ + b ₄₁ u ⁴ v + b ₂₃ u ² v ³ + b ₀₅ v ⁵

Some terms in the previous formula were omitted intentionally: traditional world maps are symmetrical to the horizontal and vertical axes. This double symmetry can be achieved if x is an odd function of u and an even function of v. On the other hand, y is an even function of u and an odd function of v for the same reason. This symmetry will not be reflected by the geographic graticule (in plagal aspect, only the mapped metagraticule is symmertrical). Nevertheless, this symmetry is useful, as the map frame (i.e., the mapped South metapole) and the distribution of distortion will still be symmetrical. The author found that this constraint is useful from an aesthetical point of view. Coefficients a _ij and b _ij were chosen by optimization.

The analysis of distortion follows the usual calculations. The mapped angle ϑ between the meridians and parallels is (Snyder 1987):

Next, the linear scales are calculated in the directions of meridians and parallels:

Finally, the semi-axes a and b of the Tissot indicatrix are:

Note, that in the three formulae above for cot ϑ, h and k, one may freely use the metacoordinates instead of the geographical ones to make derivation simpler. In this case, one yields the linear scales along metameridians and metaparallels for h and k, but a and b should remain the same.

The overall distortion value containing both the effects of the areal and angular distortions over large areas S can be measured effectively using the Airy-Kavrajskiy criterion (Frančula 1971):

This integral was evaluated numerically using two-point Gaussian quadrature generalized for irregular spherical polygons (Kerkovits 2020). Coastline coordinates were extracted from the Natural Earth (Kelso and Patterson, 2021) database.

The minimum search for Ewas carried out by a modified downhill simplex method (Kaczmarczyk, n. d.). To avoid reporting local minima, the algorithm restarted the downhill simplex method near the termination point of the previous run, and accepted the result only if two successive optimizations yielded (approximately) the same minimum. This was crucial: the optimization problem was not well-behaving, the downhill simplex method tended to converge to local minima.

4 Results of the Optimization

It turned out that simultaneous optimization of the aspect parameters φ _P , λ _P , λ' ₀, and coefficients a _ij , b _ij made the downhill simplex method unreliable, just asCanters (2002) observed. The method reported various local minima, and the convergence was very slow. Especially, the aspect parameters remained close to the initial values. Therefore, optimization was performed in a two-step process.

The first initial value was the oblique azimuthal equidistant projection ( a ₁₀ = b ₀₁ = 1, other a _ij , b _ij coefficients are 0) centred on 45°S 95°W like the azimuthal projections ofSpilhaus (1983). In the first step of the optimization, only the aspect parameters, φ _P , λ _P , λ' ₀, and the linear coefficients a ₁₀ and b ₀₁ were allowed to change. This allowed the method to extensively explore the parameter space regarding the effect of the aspect parameters, while the main characteristics of the distortion pattern remained intact. The result was assumed to have a set of aspect parameters close to the optimal. Thus, it was the starting value for the next optimization, where all parameters (even those that had already been optimized in the previous step) were allowed to change.

Running a naïve optimization for the full area of the world ocean (excluding the Caspian Sea) obtained the following values for the coefficients:

The Airy-Kavrayskiy criterion is: E = 0.440089.

These coefficients result in an unusable map projection (Fig. 1). The map frame is self-intersecting, and some lands are overlapping even near the area of optimization. Inclusion of narrow and long seas (such as the Red Sea) in the area of optimization is also responsible for the suboptimal result: being far from the large water bodies, they have large distortions. The optimization tried to reduce it as much as possible, at the expense of distortions in the three large oceans.

To improve results, the map frame was made convex. This condition was implemented as follows: coordinates along the map frame were calculated for each 1° metalongitude. The resulting polygon was first examined for self-intersections using the Shamos-Hoey algorithm (Shamos and Hoey 1976). If no intersections were reported, then cross products of vectors starting from each vertex were calculated. If all cross products had the same sign in the third coordinate, the polygon was convex. If any of the previous conditions fails, the algorithm assigned the floating-point representation of infinity to E without actually calculating it, so that the downhill simplex would avoid entering this part of the parameter space. The final coefficients are:

The Airy-Kavrayskiy criterion is: E = 0.475545, which indicates only 8 % increase of distortion compared to the unconstrained optimization.

The resulting map (Fig. 2 and3) became more usable, and its distortions were reduced on lands, so the coastlines are easier to recognize. This mapping is a much more useful tool than the previous one for creating maps of the World Ocean. The removal of the overlap did not increase the distortion significantly (in fact, there are areas, like the Gulf of Guinea and the western coasts of the Pacific Ocean, where the distortions slightly decreased). This variant is recommended over the previous one.

Another variant of this projection was created by excluding long, inland seas (Baltic Sea, Mediterranean Sea, Red Sea, Persian Gulf) from the area of the optimization. Convexity of the map frame was enforced also in this version. It was expected that the distortions can be reduced a bit further in the area of the large oceans. The result is:

The Airy-Kavrayskiy criterion is: E = 0.435487, however, it is not comparable to previous values, as it now corresponds to a slightly smaller area.

The map shown inFig. 4 does exhibit lower distortions in large oceans, but we must pay a high price for it: the Mediterranean Sea is extremely distorted, and the Caspian Sea became flattened at the left edge. These parts of the mapping are barely usable, so the map editor should probably cut them off before designing a map in this variant. The three large Oceans would fit in a vertical elliptical shape, which could be used as a map frame. Nevertheless, these disadvantages might hinder the usefulness of this variant, so the projections ofFigs. 2 -3 are preferred by the author.

5 Conclusions

Figs. 2 -4 show a map of the World Ocean in a way that is acceptable for use in cartography. Although distortions were optimized, the lack of discontinuities has a disadvantage: there are still severe distortions near the coastlines. Leaving the inland seas out of the optimization, distortions can be improved in the larger water bodies, but the inland seas become quite unreadable, so that variant is useful only if the map thematic does not extend to these seas at all.

Besides the previously mentioned disadvantages, the proposed map projection is one of those few mappings that can show the World Ocean as a single, continuous unit. As the map has no discontinuities even across lands, it can be used for maps of global relations across the World Ocean. The map has significantly lower distortion in oceans than the oblique azimuthal equidistant, which is now the only ubiquitous aphylactic mapping that can display the World Ocean without any discontinuity.

The experiences gained while tackling the problems during the optimizations may be useful for any other, even completely unrelated research in the field of low-distortion map projections.

1 Kartografske projekcije Svjetskog oceana

Nedavna se istraživanja kartografskih projekcija ponekad više fokusiraju na kontinente nego na oceane. Na primjer,Cantersove (2002) karte s malom distorzijom optimirane su za kontinente, a zanemarene su distorzije na oceanima.

Dok uobičajene karte svijeta nemaju nikakve značajne podatke o oceanima (npr. političke, poljoprivredne, etnografske karte), oceanografska su istraživanja također u porastu proizvodeći podatke koji se koncentriraju na Zemljinu hidrosferu. Kartografske bi projekcije za takve teme trebale imati područja male distorzije na oceanima. U ovom se radu pojam Svjetski ocean odnosi na Tihi, Indijski i Atlantski ocean zajedno sa svim susjednim morima (ne uključujući Kaspijsko jezero).

Prve su se karte prilagođene Svjetskom oceanu kao jedinstvenoj cjelini počele pojavljivati sredinom 20. stoljeća. Kao jedan od prvih pokušaja izrade karte Svjetskog oceana može se spomenuti Bartholomewova tetraedarska projekcija iz 1942. sa središtem na Južnom polu (Snyder 1993). Međutim, ta je rana karta imala ozbiljne diskontinuitete u Tihom oceanu i prikazivala je Arktički ocean izrezan na tri dijela.

Vjerojatno je većinu preslikavanja Svjetskog oceana dizajnirao Spilhaus. Njegove su karte razvijene s pomoću dviju različitih osnovnih ideja, a njegove su ranije projekcije primjenjivale prijašnja poznata preslikavanja, poput Hammerove, Augustove ili Adamsove projekcije u kosim poprečnim ili plagalnim aspektima (Spilhaus 1942,1983,Wray 1974). Očigledni ciljevi pri odabiru parametara aspekta nisu bili samo smanjenje distorzije oceana, već i prikazivanje Svjetskog oceana kao jedne, kontinuirane cjeline. Međutim, drugi cilj Spilhaus nije mogao u potpunosti ostvariti. Njegove projekcije prekidaju Svjetski ocean ne samo preko Beringovog tjesnaca (što može biti prihvatljiv kompromis), već su i značajni dijelovi Karipskog mora također isječeni na njegovim kartama. Ovisno o točnom dizajnu, mogu se uočiti i drugi diskontinuiteti u blizini obala Tihog oceana ili u Južnom kineskom moru.

Razlog tome je što uobičajene kartografske projekcije imaju rez na geografskoj dužini od 180°. Za karte kopna to nije veliki problem budući da se centriranjem karte na geografsku dužinu 10°E taj diskontinuitet pomiče na meridijan 170°W presijecajući samo nekoliko sićušnih otoka u blizini Beringovog prolaza. Međutim, taj se diskontinuitet proteže polovicom velike kružnice, što vrijedi čak i za karte u rotiranim aspektima. S druge strane, Svjetski ocean ima toliki opseg da je nemoguće postaviti polovicu velike kružnice tako da ne presijeca neku veliku vodenu površinu. Stoga bi samo sofisticiranija kartografska projekcija s manje diskontinuiteta mogla dati kontinuirani prikaz u plagalnom aspektu. Neke su kasnijeSpilhaus (1983) slijedile drugi put. Prekinuo je Zemlju uzduž kompliciranih geografskih linija (uglavnom uzduž obala oceana) i izgradio složene kartografske projekcije koje prikazuju različite dijelove Zemlje u različitim preslikavanjima. Čitatelj može pronaći pojedinosti toga koncepta i detaljniju povijest oceanskih karata u drugom autorovom radu u koautorstvu (Cameron i Kerkovits 2022).

Očita prednost potonjeg pristupa je da što više diskontinuiteta dopuštamo, više se deformacije mogu smanjiti. Postavljanje diskontinuiteta uzduž prirodnih granica može omogućiti iscrtavanje određenih tema karte bez diskontinuiteta. Projekciju su s pomoću te metode nedavno razviliCameron i Kerkovits 2022.

Nedostatak je te metode što opis diskontinuiteta zahtijeva komplicirane, nepravilne linije koje se mogu pohraniti u GIS samo kao složene polilinije koje aproksimiraju teorijske granice. Nadalje, ponekad kartografi ne žele diskontinuitet uzduž kopna. Ovaj rad, stoga, predstavlja još jedan koncept stvaranja oceanskog prikaza Zemlje sa što manje diskontinuiteta.

2 Principi dizajna

Kao što je prethodno navedeno, kartografska projekcija s diskontinuitetom uzduž meridijana 180° nije dovoljna za kartu Svjetskog oceana pa je preslikavanje dizajnirano tako da gotovo nema mjesta diskontinuiteta. Međutim, dok Zemlja ima zatvorenu plohu, ravnina karte otvorena je ploha. Stoga nije moguće konstruirati homotopiju (kontinuirano preslikavanje) među njima. Uklanjanje jedne točke s površine Zemlje rezultira otvorenom plohom, što omogućuje homotopiju na ravninu. Dakle, može se zaključiti da je nužno i dovoljno prekinuti Zemljinu površinu u jednoj točki da bi se stvorila kartografska projekcija na ravninu.Spilhaus (1983) je raspravljao o toj mogućnosti i preporučio pomicanje diskontinuiteta u 45°N 85°E.

U ovom je trenutku potrebno definirati Zemljin oblik. Radi jednostavnosti bit će aproksimiran jediničnom sferom.. Približno 20 km razlike između sfere i stvarnog Zemljinog oblika može se sa sigurnošću zanemariti na kartama sitnog mjerila.

Među dosad poznatim kartografskim projekcijama, azimutne, pseudoazimutne i poliazimutne projekcije imaju diskontinuitet samo na Južnom polu koji se može pomaknuti u bilo koju proizvoljnu točku u plagalnom aspektu. Međutim, azimutne i pseudoazimutne projekcije imaju ozbiljne distorzije u vanjskoj hemisferi pa su neprihvatljivi kandidati za kartu svijeta. Poliazimutna su preslikavanja komplicirana i nejasna, njihovu korisnost za karte svijeta još nitko nije istražio. Odabirom samo jedne točke diskontinuiteta neizbježno je da će distorzije porasti u usporedbi s tradicionalnim kartama svijeta (kao nuspojava manjeg diskontinuiteta) pa se moraju ograničiti naprednim metodama: projekcija po mjeri mora se razviti upotrebom numeričke optimizacije.

Projekcije koje imaju diskontinuitet u jednoj točki uvijek će imati beskonačno linearno mjerilo duž metaparalele u toj točki. To je lako vidjeti: ta je točka preslikana na granicu karte (zatvorena krivulja) tako da se ta beskonačno mala točka rasteže na konačnu liniju. Stoga tu točku treba pomaknuti što dalje od područja interesa kako bi se optimirala deformacija. To se najprikladnije postiže sustavom koordinatnog metasustava koji je uveoWray (1974). Pod pretpostavkom da je točka diskontinuiteta na Južnom polu, koordinatna mreža se okreće u prostoru. Rotirani parnjaci linija kartografske mreže označavaju se prefiksom meta-. Primjenom formula projekcije na metageografsku širinu i metageografsku dužinu umjesto na geografsku širinu i dužinu, diskontinuitet će se pomaknuti na slobodno odabrani južni metapol. Ako kutovi rotacije nisu višekratnici pravog kuta, kaže se da je kartografska projekcija u plagalnom aspektu.

Optimizaciju kartografskih projekcija detaljno je razmatraoCanters (2002). Naveo je da se postojeće projekcije mogu proizvoljno mijenjati upotrebom polinomskih transformacija. Polinomi mogu aproksimirati bilo koju glatku funkciju tako da to, također, može biti razumna aproksimacija najbolje moguće kartografske projekcije. Međutim, početna projekcija mora biti pažljivo odabrana: polinomi mogu samo aproksimirati glatka preslikavanja, tako da nikada ne unose niti poništavaju diskontinuitete i ne mogu poništiti beskonačne deformacije početne karte. Na primjer, ako je stereografska projekcija odabrana kao početna projekcija, južni metapol bit će beskonačno daleko na karti, bez obzira na polinom. S druge strane, Lambertova ekvivalentna azimutna projekcija ima linearno mjerilo jednako nuli u smjeru metameridijana na južnom metapolu (beskonačno komprimira sadržaj karte u smjeru meridijana). To, također, ne može biti promijenjeno nikakvom transformacijom s pomoću polinoma. Razumno je pretpostaviti da takve beskonačne distorzije nisu prisutne u optimalnoj projekciji (u ovom se radu pojam optimalna odnosi na kartografsku projekciju koja ima najmanju moguću distorziju prema nekom kriteriju distorzije; to nema utjecaja na njezinu praktičnu korisnost uopće), tako da je azimutna ekvidistantna projekcija jednostavan kandidat za početnu projekciju.

3 Matematička osnova

Budući da će se ova projekcija koristiti u plagalnom aspektu, treba koristiti metageografsku širinu φ' i metageografsku dužinu λ' umjesto geografske φ i dužine λ (Snyder 1987,Lapaine i Frančula 2016):

Ovdje koordinate φ _P i λ _P metapola (koje određuju središte za glavnu temu karte, a to je Svjetski ocean) i azimut λ' ₀ početnog metameridijana mogu biti predmet optimizacije.

U sljedećem se koraku azimutna ekvidistantna projekcija (Snyder 1987) primjenjuje na metakoordinate (koordinate za posrednu ravninu označene su s u i v):

Konačno, ta se karta transformira s pomoću polinoma petog stupnja:

x = a ₁₀ u + a ₃₀ u ³ + a ₁₂ uv ² + a ₅₀ u ⁵ + a ₃₂ u ³ v ² + a ₁₄ uv ⁴

y = b ₀₁ v + b ₂₁ u ² v + b ₀₃ v ³ + b ₄₁ u ⁴ v + b ₂₃ u ² v ³ + b ₀₅ v ⁵

Neki su članovi u prethodnoj formuli namjerno izostavljeni: tradicionalne karte svijeta simetrične su na vodoravnu i okomitu os. Ta se dvostruka simetrija može postići ako je x neparna funkcija od u i parna funkcija od v. S druge strane, y je parna funkcija od u i neparna funkcija od v iz istog razloga. Ta se simetrija neće reflektirati na kartografsku mrežu (u plagalnom aspektu, samo je slika metamreže simetrična). Unatoč tome, ta je simetrija korisna, jer će okvir karte (tj. slika južnog metapola) i distribucija distorzije i dalje biti simetrični. Autor je utvrdio da je to ograničenje korisno s estetskog gledišta. Koeficijenti a _ij i b _ij dobiveni su optimizacijom.

Analiza distorzija slijedi iz uobičajenog računanja. Preslikani kut ϑ između meridijana i paralela je (Snyder 1987):

Zatim se računaju faktori linearnih mjerila u smjerovima meridijana i paralela:

Konačno, poluosi a i b Tissotove indikatrise su:

Uočimo da se u trima gornjim formulama za ϑ, h i k mogu slobodno koristiti metakoordinate umjesto geografskih kako bi se izvođenje učinilo jednostavnijim. U tom slučaju dobivamo faktore linearnih mjerila uzduž metameridijana i metaparalela za h i k, ali a i b ostaju isti.

Ukupna se vrijednost distorzije koja sadrži učinke distorzije površina i kutova na velikim područjima S može učinkovito izmjeriti upotrebom kriterija Airy-Kavrajskoga (Frančula 1971):

Taj je integral numerički procijenjen s pomoću Gaussove kvadrature u dvjema točkama, generalizirane za nepravilne sferne poligone (Kerkovits 2020). Koordinate obale izvučene su iz baze podataka Natural Earth (Kelso i Patterson, 2021). Traženje minimuma od E provedeno je primjenom modificirane silazne simpleks metode (Kaczmarczyk, n. d.). Da bi se izbjeglo prijavljivanje lokalnih minimuma, algoritam ponovno pokreće silaznu simpleks metodu blizu točke završetka prethodnog izvođenja i prihvaća rezultat samo ako su dvije uzastopne optimizacije dale (približno) isti minimum. To je bilo presudno: problem optimizacije nije se dobro ponašao, silazna simpleks metoda težila je konvergirati lokalnim minimumima.

4 Rezultati optimizacije

Ispostavilo se da istovremena optimizacija parametara aspekta φ _P , λ _P , λ' ₀ i koeficijenata a _ij , b _ij čini silaznu simpleks metodu nepouzdanom, baš kao što je primijetioCanters (2002). Metoda je prijavila različite lokalne minimume, a konvergencija je bila vrlo spora. Konkretno, parametri aspekta ostali su blizu početnih vrijednosti pa je optimizacija provedena u dva koraka.

Prva je početna vrijednost bila kosa azimutalna ekvidistantna projekcija ( a ₁₀ = b ₀₁ = 1, ostali koeficijenti a _ij , b _ij su 0) sa središtem na 45°S 95°W poput azimutnih projekcijaSpilhaus (1983). U prvom je koraku optimizacije dopuštena samo promjena parametara aspekta φ _P , λ _P , λ' ₀ i linearnih koeficijenata a ₁₀ i b ₀₁ . To je omogućilo metodi da opsežno istraži prostor parametara u pogledu učinka parametara aspekta, dok su glavne karakteristike uzorka distorzije ostale netaknute. Pretpostavlja se da rezultat ima skup parametara aspekta blizu optimalnog. Dakle, to je bila početna vrijednost za sljedeću optimizaciju, gdje je svim parametrima (čak i onima koji su već bili optimirani u prethodnom koraku) bila dopuštena promjena.

Provođenjem naivne optimizacije za cijelo područje Svjetskog oceana (isključujući Kaspijsko jezero) dobivene su sljedeće vrijednosti za koeficijente:

Kriterij Airy-Kavrayskoga E = 0.440089.

Ti koeficijenti rezultiraju neupotrebljivom kartografskom projekcijom (slika 1). Okvir karte se sam siječe, a neka se zemljišta preklapaju čak i blizu područja optimizacije. Uključivanje uskih i dugih mora (kao što je Crveno more) u područje optimizacije također je odgovorno za suboptimalan rezultat: budući da su udaljena od velikih vodnih tijela, ona imaju veliku distorziju. Optimizacija ju je na račun distorzija u trima velikim oceanima pokušala smanjiti što je više moguće.

Figure 1. Unconstrained optimal map projection of the World Ocean / Slika 1. Bezuvjetna optimalna kartografska projekcija Svjetskog oceana

Da bi se poboljšali rezultati, okvir karte je učinjen konveksnim. Taj je uvjet primijenjen na sljedeći način: koordinate uzduž okvira karte izračunane su za svaki 1° metadužine. Rezultirajući je poligon prvo ispitan na samopresjek s pomoću algoritma Shamosa-Hoeya (Shamos i Hoey 1976). Ako nisu prijavljena nikakva sjecišta, tada su izračunani vektorski produkti počevši od svakog vrha. Ako su svi vektorski produkti imali isti predznak treće koordinate, poligon je bio konveksan. Ako bilo koji od prethodnih uvjeta ne uspije, algoritam je veličini E dodijelio vrijednost beskonačno bez da ju je zapravo izračunao, tako da bi silazna simpleks metoda izbjegla ulazak u taj dio prostora parametara. Konačni su koeficijenti:

Kriterij Airy-Kavrayskoga E = 0.475545 ukazuje na povećanje distorzije od samo 8 % u usporedbi s optimizacijom bez uvjeta.

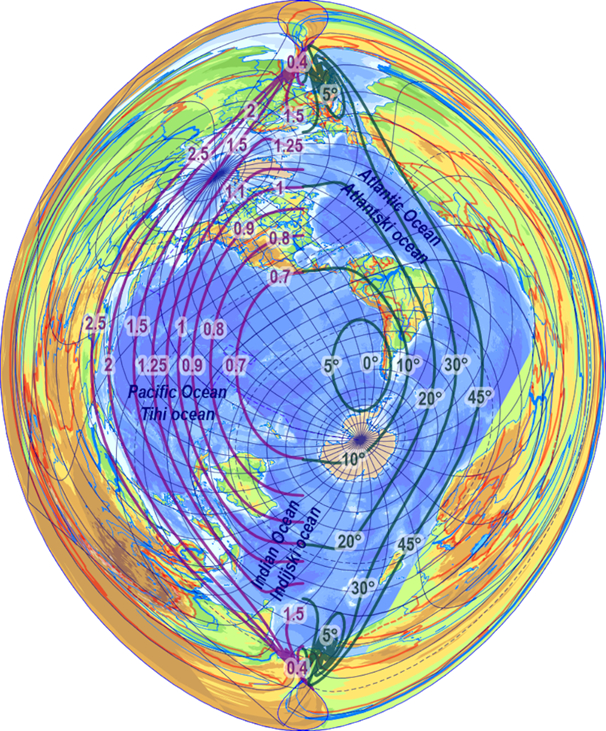
Dobivena je karta (sl. 2 i3) postala upotrebljivija, a njezina je distorzija smanjena na kopnu pa su obale lakše prepoznatljive. To je preslikavanje mnogo korisniji alat za izradu karata Svjetskog oceana od prethodnoga. Uklanjanje preklapanja nije značajno povećalo distorziju (zapravo, postoje područja, poput Gvinejskog zaljeva i zapadnih obala Tihog oceana, gdje su se distorzije malo smanjile). Ta se varijanta preporučuje u odnosu na prethodnu.

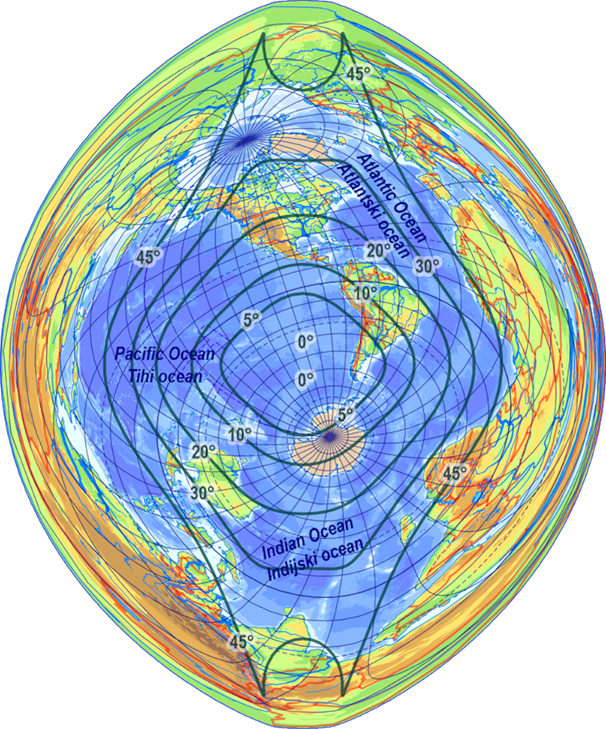
Figure 2. Optimal map projection of the World Ocean in a convex frame (isolines of areal scale) / Slika 2. Optimalna kartografska projekcija Svjetskog oceana u konveksnom okviru (izolinije prikazuju mjerilo površina)

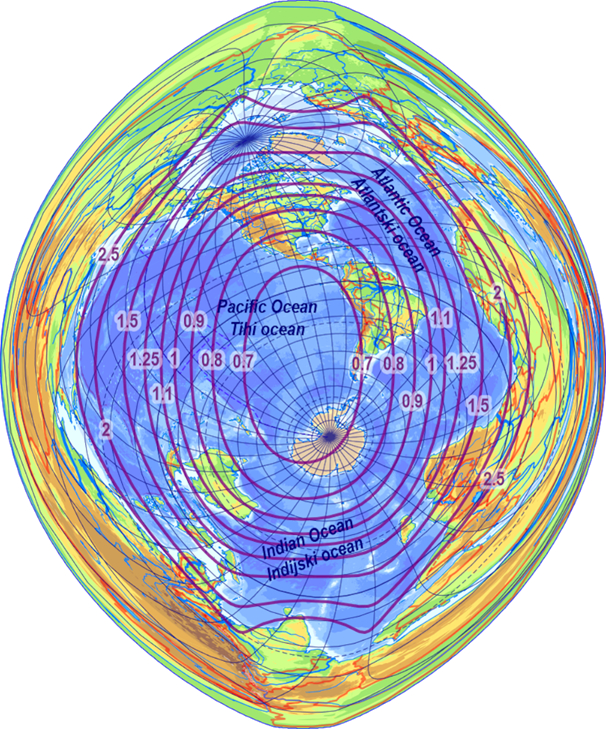
Figure 3. Optimal map projection of the World Ocean in a convex frame (isolines of maxi-mum angular deviation) / Slika 3. Optimalna kartografska projekcija Svjetskog oceana u konveksnom okviru (izolinije prikazuju maksimalno kutno odstupanje)

Druga je varijanta te projekcije nastalae isključivanjem dugih, unutarnjih mora (Baltičko more, Sredozemno more, Crveno more, Perzijski zaljev) iz područja optimizacije. Konveksnost okvira karte također je nametnuta u ovoj verziji. Očekivalo se da će se distorzije još malo smanjiti u području velikih oceana. Rezultat je:

Kriterij Airy-Kavrayskoga E = 0.435487, međutim ta vrijednost nije usporediva s prethodnim vrijednostima jer sada odgovara nešto manjem području.

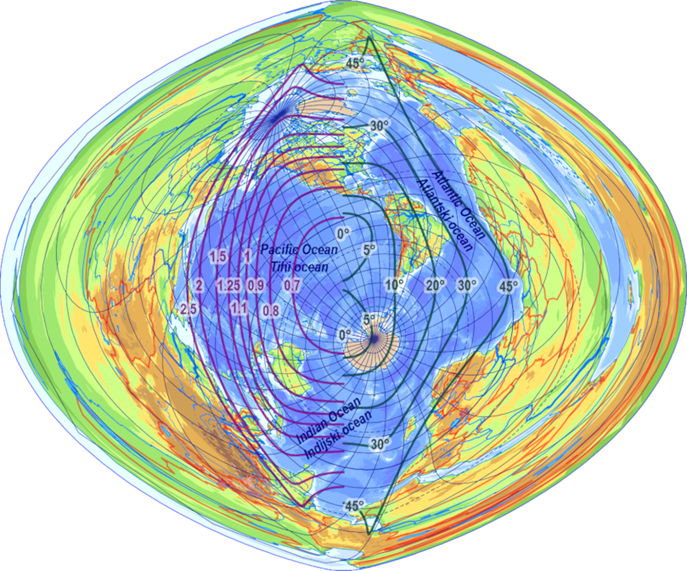
Karta prikazana naslici 4 pokazuje manju distorziju velikih oceana, ali moramo za to platiti visoku cijenu: Sredozemno je more izuzetno iskrivljeno, a Kaspijsko je jezero na lijevom rubu postalo spljošteno.. Ti su dijelovi preslikavanja jedva upotrebljivi pa bi ih urednik karte vjerojatno trebao odrezati prije dizajniranja karte u toj varijanti. Tri bi velika oceana stala u okomiti eliptični oblik koji bi se mogao koristiti kao okvir karte. Ipak, ti nedostatci mogu spriječiti upotrebljivost ove varijante tako da autor preferira projekcije nasl. 2 i3.

Figure 4. Optimal map projection of the World Ocean in a convex frame (inland seas exclud-ed) / Slika 4. Optimalna kartografska projekcija Svjetskog oceana u konveksnom okviru (bez unutarnjih mora)

5 Zaključci

Slike 2 -4 prikazuju kartu Svjetskog oceana na prihvatljiv način za upotrebu u kartografiji. Iako su distorzije optimirane, nedostatak diskontinuiteta ima ovu manu: još uvijek postoje ozbiljne distorzije u blizini obalnih linija. Izostavljanjem unutarnjih mora iz optimizacije, distorzije se mogu poboljšati u većim vodnim tijelima, ali unutarnja mora postaju prilično nečitljiva, tako da je ta varijanta korisna samo ako se tema karte ne proteže na ta mora.

Uz prethodno navedene nedostatke, predložena kartografska projekcija jedno je od onih rijetkih preslikavanja koja mogu prikazati Svjetski ocean kao jednu, kontinuiranu cjelinu. Kako karta nema diskontinuiteta čak ni preko kopna, može se koristiti za karte globalnih odnosa na Svjetskom oceanu. Karta ima značajno manju distorziju u oceanima od kose azimutalne ekvidistante koja je sada jedina sveprisutna afilaktička karta koja može prikazati Svjetski ocean bez ikakvog diskontinuiteta.

Iskustva stečena rješavanjem problema tijekom optimizacija mogu biti korisna za druga istraživanja na području kartografskih projekcija s malom distorzijom.