1. Introduction
Map projections are mappings of a curved surface, especially an ellipsoid or a sphere, into a plane (Lapaine 2017). Most often, they are given analytically by basic cartographic equations x=x(φ,λ), y=y(φ,λ) , where φ,λ are geographic or geodetic coordinates, and x, y are coordinates in the projection plane. They can also be specified by a table of coordinates or a description of the construction of the cartographic network (Frančula 2004).
Although they are called projections, they should not be equated with projections in descriptive geometry. In fact, we are talking about the mapping of a curved surface into a plane. Map projections can be classified into several classes or groups according to different criteria.
According to their mapping properties, they are divided into conformal, equivalent, equidistant and conditional projections. According to the position of the projection axis, they are divided into normal, transverse and oblique projections. According to the shape of the network of pseudomeridians and pseudoparallels, they are divided into conic, cylindrical, azimuthal, pseudoconic, pseudocylindrical, pseudoazimuthal, polyconic, circular and other projections (Lapaine, Frančula 2022).
Map projections often bear the name of their author, eg Mercator, Winkel Triple, Robinson. As a special group of map projections, geodetic projections, i.e. projections for the needs of the state survey, are often singled out.
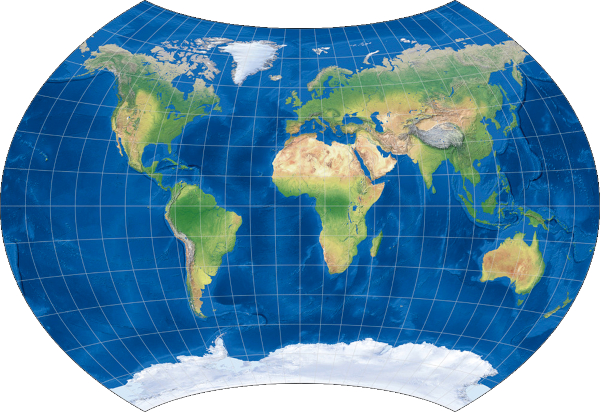
Map projections are necessary because the Earth is curved in shape, which is not possible to represent on a flat surface without distortion. Different map projections are used for different purposes, depending on the desired level of accuracy and the specifics of the area being mapped. For example, a map projection that is good for showing the whole world often may not be suitable for showing the details of a small region, nor to display the continents. For example, if we cut out the map of Africa (Figure 1b) from the world map created in the Eckert IV projection (Figure 1a),, we will get an unnecessarily elongated image of that continent. The correct choice of projection for the map of Africa is, for example, the azimuthal equivalent projection (Figure 1c).
Figure 1a. Map of the world in the Eckert IV projection / Slika 1a. Karta svijeta u projekciji Eckert IV
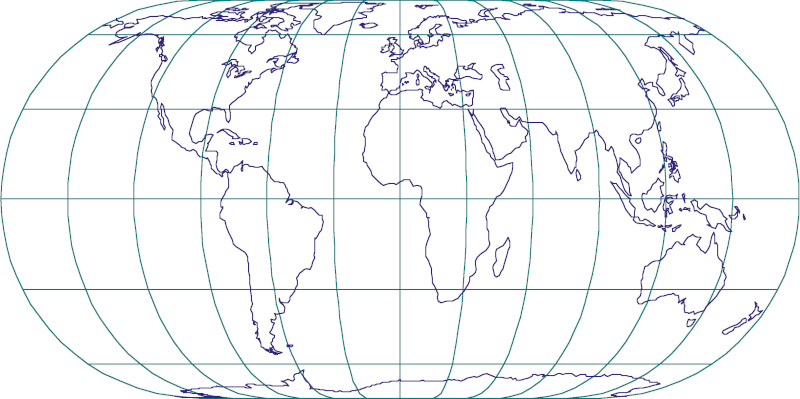
Figure 1b. Map of Africa in the Eckert IV projection – poor choice of projection for a map of Africa / Slika 1b. Karta Afrike u projekciji Eckert IV – loš izbor projekcije za kartu Afrike
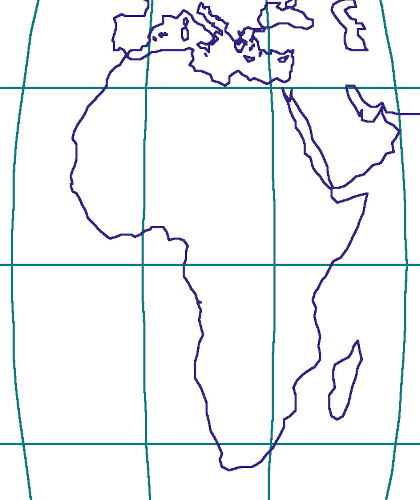
Figure 1c. Map of Africa in the Azimuthal Equivalent Projection – a good choice of projection for the map of Africa / Karta Afrike u azimutnoj ekvivalentnoj projekciji – dobar izbor projekcije za kartu Afrike
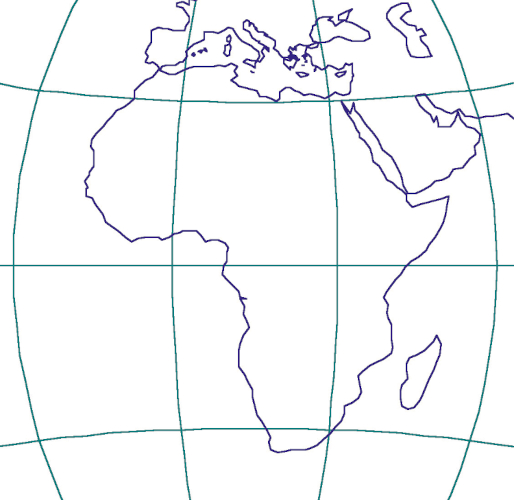
The use of map projections enables the numerical determination of distortions and their exclusion from the data taken from the maps. Map distortions are changes in lengths, area, angles and shapes resulting from the application of map projection.
The main problem in cartography is that it is not possible to map a spherical or ellipsoidal surface into a plane without distortion (Lapaine 2023). A poorly chosen map projection can actually be harmful. We tend to believe what we see, and when basic geographic relationships, such as shapes, sizes and directions are badly distorted, we tend to accept them as fact if we see them that way on maps. This can lead to very wrong impressions. For example, that the route from New York to Tokyo eastward, or that Greenland is only slightly smaller in size than Africa, although it is about 14 times smaller than Africa (Figures2a and2b) Our mental maps, the geographic "database" of the brain, are generated mostly from what we look at. Since globes are not common, most mental images of the Earth come from flat maps. A heavily distorted map view that is seen regularly (such as the one in the background of some television news) will after a while look familiar and therefore "look right". This can cause one's mental map of the world to become permanently distorted. Since no map projection provides a single scale across the entire area, it is important to determine to what extent it varies on the map. For example, on a world map, the qualitative distortion is obvious to the eye familiar with maps. It is possible to see to what extent land masses are inappropriately sized or changed in shape and to what extent meridians and parallels do not intersect at right angles or are not evenly distributed. On maps of countries or even continents, the distortion may not be visible to the eye, but becomes visible after careful measurement and analysis.
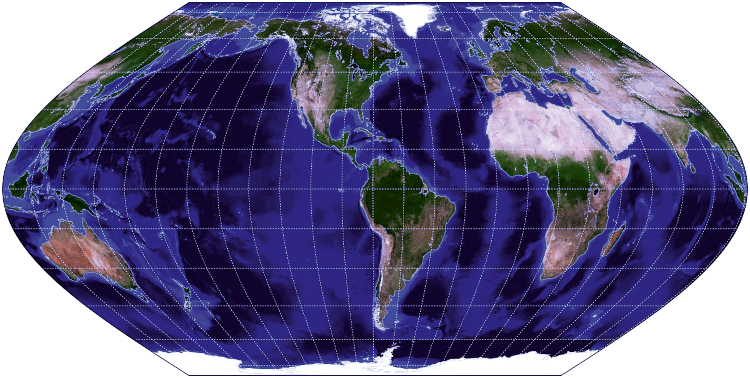
Figure 2a. World map in Mercator projection - a bad choice of projection for a world map (produced with G.Projector software and data world_topo_bathy_200407.jpg) / Slika 2a. Karta svijeta u Mercatorovoj projekciji – loš izbor projekcije za kartu svijeta (izrađeno s pomoću sotvera G.Projector i podataka world_topo_bathy_200407.jpg)
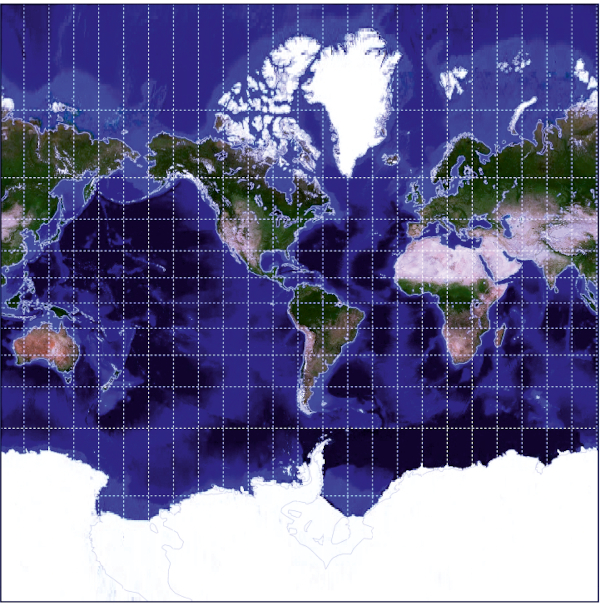
Figure 2b. World map in Eckert VI projection – a good choice of projection for the world map (produced with G.Projector software and data world_topo_bathy_200407.jpg) / Slika 2b. Karta svijeta u projekciji Eckert VI – dobar izbor projekcije za kartu svijeta (izrađeno s pomoću sotvera G.Projector i podataka world_topo_bathy_200407.jpg)
In 1777, Euler was the first to prove that there is a map without distortions. All map projections contain distortions of area, angles and/or distances. Some distortions can be controlled to preserve certain characteristics, but map projections then distort other characteristics of the displayed object.
The classic way of showing the distortions of a projection is the use of Tissot's indicatrix or deformation ellipses.Tissot (1881) described the construction of an ellipse that locally displays the amount and orientation of distortion components. Namely, every map projection can be locally approximated by affine mapping. By mapping a circle of infinitesimally small radius, an ellipse is obtained, which we call the distortion ellipse or Tissot's indicatrix. The axes of this ellipse are called the main directions and along them the local linear scale is the largest and smallest. Tissot's indicatrix is often used to illustrate scale variation on a map.
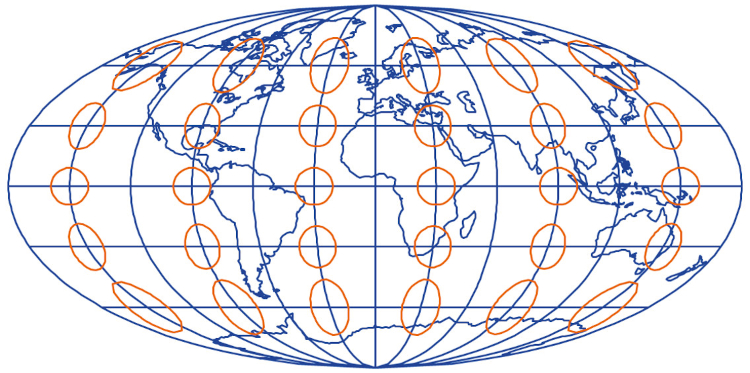
One indicatrix describes distortions at one point. Since distortions vary on the map, Tissot indicatrixes are generally placed at multiple locations on the map to illustrate the spatial distribution of distortions. The usual scheme places them at each intersection of the shown meridians and parallels (Figure 3). These schemes are important in the study of map projections, both for illustrating the distribution of distortions and for providing a basis for calculating the magnitude of distortions at each point.
On maps made in conformal projections Tissot's indicatrices are circles whose size varies depending on the location. On maps made in equivalent projections, all Tissot indicatrices have the same area, although their shapes and orientations differ depending on the location. In arbitrary projections, both the area and the shape of the indicatrix vary on the map.
Figure 3. Map of the world in the Apian II projection with Tissot's indicatrices / Slika 3. Karta svijeta u projekciji Apian II s ucrtanim Tissotovim indikatrisama
In the 1970s, Konusova proposed a local criterion. That criterion is the angular value. Let us call it the classification angle. The classification angle α is calculated as follows:
where a and b are the semi-axes of the deformation ellipse. Let us consider that formula in more detail.
In conformal projections at any point on the map, the linear scale does not depend on the direction a = b, so α=0. In equivalent projections, ab = 1, therefore, α=π/2. In equidistant projections, the effects of distortion of shapes (angles) and area are the same; in the formula, the numerator is equal to the denominator, α=π/4. Therefore, the quantitative assessment of the classification of projections according to the nature of the distorions based on the value of the classification angle can be carried out in the following way:
α=0 − conformal projections
α=π/4 − equidistant projections
α=π/2 − equivalent projections
In order to compare map projections with regard to their distortion characteristics, it is convenient to quantify the total distortion with a single measure. It is not as simple as it may seem.Tissot (1881) proposed to characterize the distortion of the map projection by the maximum value reached in the mapped area. Maximum distortion values can be calculated, but they have one major drawback. It does not take into account how the distortion is spatially distributed. To account for spatial variations in distortion, local measures can be integrated over the region of interest. The criteria of Jordan, Airy, Airy-Kavrayskiy and others are known.
It is important to note that all distortions can be eliminated if we know in which map projection the map was made. Cartographers usually want to create a map with as little distortion as possible. However, in some cases the approach is reversed. A cartogram (also a value area map or an anamorphic map) is a thematic map on which the distances in a line network or the area of territorial, usually administrative, units are deliberately distorted (Lapaine 2023).
Map projection is essential for navigation, especially for sailors and pilots who use charts for navigation. A loxodrome is a curve in a surface of rotation that intersects meridians at a same angle. A ship sails on loxodromes when it sails constantly on the same course on the way between two positions. In the normal aspect Mercator projection, loxodromes are straight lines. An orthodrome is a geodesic line on a sphere and therefore a part of a great circle. A ship sailing on an orthodrome takes the shortest route between two positions. However, on a map made in the normal aspect Mercator projection, the arc of the loxodrome between two points is shorter than the arc of the orthodrome connecting those same two points.
When expressing the problems it considers and when finding their analytical solutions, the theory of map projections applies the settings of many mathematical disciplines, such as plane and spherical trigonometry, differential geometry, differential and integral calculus, methods of numerical analysis, etc. Data on the shape and size of the Earth and coordinates points of the geodetic base and astronomical points, the theory of map projections takes over from geodesy and geodetic astronomy. The mutual connection of the theory of map projections with geography and other sciences, for the needs of which a large number of various maps are made, is also clearly expressed.
The basic tasks of the theory of map projections are as follows:
dissemination of knowledge about map projections;
development of the theory of map projections, primarily in the field of obtaining the best map projections, including "best" and "ideal";
examination of different map projections, their essence, properties, interdependence and efficiency of application in practice;
improvement of existing map projections and their standardization;
research into the role of map projections and their application in geoinformation systems;
improvement of research methods for new map projections, especially algorithms and appropriate software with improvements in computing techniques;
elaboration of other mathematical elements of the map, such as scale, division into sheets, etc., which appear in multi-sheet editions;
examining and solving tasks of a mathematical nature that appear when compiling maps (eg transforming map projections using various aids, including computers);
elaboration of the theory and methods of automation in the application of map projections.
2. Historical Development of Map Projections
The development of map projections ran parallel to the development of map making and cartography in general. The development of many sciences, technical achievements and the needs of everyday life over time have initiated ever wider demands for the production of various topographic and thematic maps of different scale and purpose, which required a continuous increase in the number of map projections and the improvement of the mathematical basis of the maps.
The beginnings of map projections are more then two thousand years old, since Greek scientists were the first to introduce mathematical principles into the basis of mapping the Earth and the starry sky and began to apply a network of meridians and parallels. A great role in the development of cartography was played by the works of Anaximander, Eratosthenes, Apollonius and Hipparchus (Snyder 1993).
It is believed that the first map in a projection was made by Thales from Miletus in 600 BC. It was a map of the celestial sphere in gnomonic projection. Among the oldest projections are the stereographic and orthographic ones used by the famous Greek astronomer and mathematician Hipparchus, also for making maps of the celestial sphere around 150 BC. From that time until today, several hundred map projections have been invented. In the 2nd century, Ptolemy wrote his capital work, Geography, which included a description of the compilation of maps and the determination of the Earth's dimensions, as well as the construction of map projections.
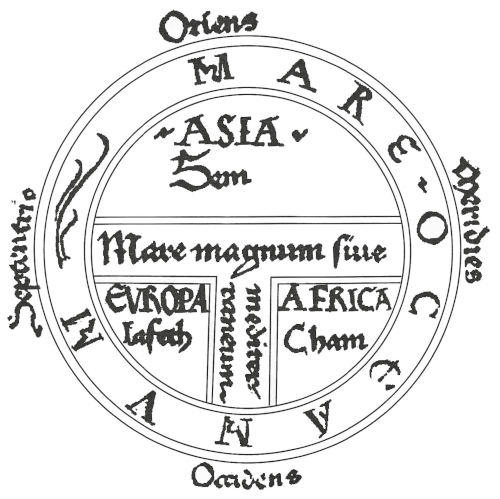
A T and O map or O–T or T–O map (orbis terrarum, with the letter T inside an O), also known as an Isidoran map, is a type of early world map that represents world geography as first described by the 7th-century scholar Isidore of Seville (c. 560–636) in his De Natura Rerum and later his Etymologiae (c. 625).Figure 4 shows the T and O map, from the first printed version of Isidore's Etymologiae, with the three known continents represented.
Figure 4. Isidoran T-O map from 1472 (https://en.m.wikipedia.org/wiki/File:Etymologiae_Guntherus_Ziner_1472.jpg) / Slika 4. Izidorska T-O karta iz 1472. godine (https://en.m.wikipedia.org/wiki/File:Etymologiae_Guntherus_Ziner_1472.jpg)
The epoch of the Middle Ages in Europe was marked by the appearance of the so-called monastery maps, which reflected the religious idea of the world without networks of coordinates and without the importance of map projections.
The special development of cartography began during the Renaissance − the period of great geographical discoveries. Accurate, reliable maps became necessary for managing the country, for military needs, for the development of trade and shipping. Such maps could only be compiled by applying the mathematical basis and the results of the land survey. Topographical maps appeared first.
At the end of the 16th and the beginning of the 17th century, a significant event in the further development and popularization of cartography was the compilation and publication of geographical atlases published by the famous Dutch cartographers Ortelius and Mercator. Mercator was the first to use the conformal cylindrical projection, which is still successfully used for maritime navigation charts.
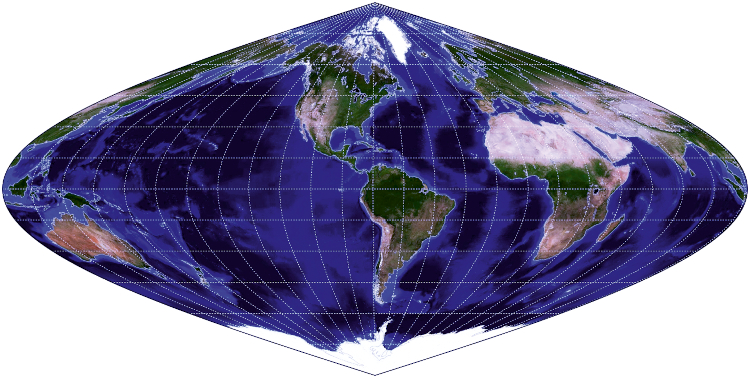
When making maps of the world and larger territories, the trapezoidal projection and the Appian projection were widely used at that time, which served as prototypes for later developed pseudocylindrical projections. In the 17th century, a new sinusoidal pseudocylindrical projection for the world map was proposed by the French cartographer Sanson (Figure 5).
Figure 5. World map in the Sinusoidal projection (produced with G.Projector software and data world_topo_bathy_200407.jpg) / Slika 5. Karta svijeta u sinusnoj projekciji (izrađeno s pomoću sotvera G.Projector i podataka world_topo_bathy_200407.jpg)
The development of the scientific basis of cartography and the beginning of the topographical study of the Earth and, as a result, a further increase in the accuracy and reliability of maps characterize the 18th century. A number of new projections proposed by Bonne (Figure 6), Lambert, Lagrange, Euler and others were introduced into cartographic practice.
Figure 6. World map in the Bonne projection (produced with G.Projector software and data world_topo_bathy_200407.jpg) / Slika 6. Karta svijeta u Bonneovoj projekciji (izrađeno s pomoću sotvera G.Projector i podataka world_topo_bathy_200407.jpg)
The Renaissance ended with the introduction of elementary mathematical analysis in the development of map projections. Such an analysis was especially applied to the Mercator projection in which loxodromes are shown as straight lines and to projections in which all shown parallels are divided by meridians at an equal distance, regardless of whether the parallels are circular arcs (Werner projection) or straight lines (sinusoidal). Map projections become more complex: instead of those whose cartographic networks are simply drawn because they consist of circular arcs and straight lines, there are those that are drawn by using tables of trigonometric functions.
Murdoch (1758) consciously set the requirement that the total area of the mapped area be correct, but he did not insist on the constancy of the local scale of the areas. The first intentional preservation of area fidelity at each point was done byLambert (1772) during his invention of cylindrical, azimuthal and conic equivalent projections. Halley geometrically proved the conformality of the stereographic projection, and Lambert did it with differential calculus and also invented three new conformal projections. Many map projections were created in the 19th and 20th centuries, but the basic principles were laid down by 1772 and especially in that year.
The most significant contribution of cartographers, surveyors and mathematicians of the 19th century to the theory of map projections was the establishment of solid mathematical principles. Lambert and Lagrange made a significant start in the 1770s, but Gauss and Tissot in particular made major contributions until the 1880s. Other researchers, such as Airy, Clarke, Schwartz and Peirce (Figure 7) focused on more specific but complex tasks, while Germain, Gretschel and Craig collected the various works of other scientists into separate monographs. New projections by Mollweide, Albers, Gall, and others contain simpler applications of mathematics, but still deserve names after their inventors. The accelerated development of the theory of map projections in that period can be seen in the large number of new projections and the number of published books and articles (Snyder 1993).
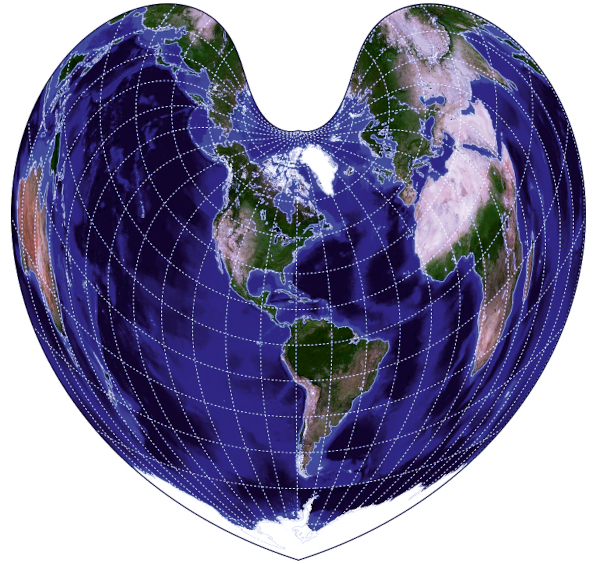
Figure 7. World map in the Peirce quincuncial projection (produced with G.Projector software and data world_topo_bathy_200407.jpg) / Slika 7. Karta svijeta u Peircejevoj kvinkunksnoj projekciji (izrađeno s pomoću sotvera G.Projector i podataka world_topo_bathy_200407.jpg)
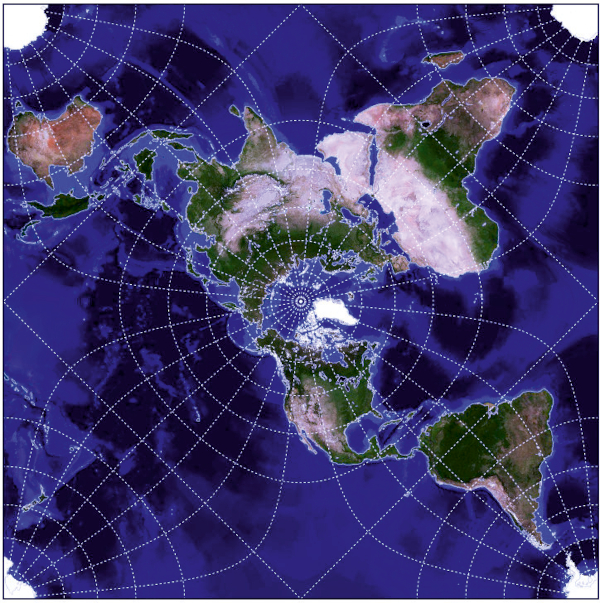
According toFrischauf (1905), the beginning of the theory of mapping one surface to another belongs to Lambert, who in Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten (Notes and additions to the basis of land and sky maps) in the third part of his Beyträge zum Gebrauch der Mathematik und deren Anwendung (Contributions to the use of mathematics and its applications, 1772,Figure 8), dealt with the generally set task of mapping the sphere and spheroid into a plane. Lambert's colleague Lagrange was inspired by his separation of variables in the expression for the differential of arc length in conformal mapping and solved the problem of conformal mapping of surfaces of revolution and published it in two treatises Sur la construction des cartes géographiques (On the construction of geographic maps, Nouveaux Mémoires de l'Académie Royal de Berlin, 1779).
Figure 8.Lambert J H (1772) Beiträge zum Gebrauche der Mathematik und deren Anwendungen, Dritter Theil − front page. / Slika 8.Lambert J H (1772) Beiträge zum Gebrauche der Mathematik und deren Anwendungen, Dritter Theil − naslovnica

At the beginning of the 19th century, military institutions began to produce topographical maps on a large scale, for which the mathematical basis is of particular importance because distances and directions were determined on these maps. In 1822, the Royal Scientific Society in Copenhagen posed a prize question: find a general solution to the task – to map a part of a given surface onto another given surface so that the image is similar to the original in the smallest parts. Gauss was awarded the prize for solving the problem. This work was first published in Schumacher's Astronomische Abhandlungen in 1825. Lagrange's and Gauss's discussions are contained in volume number 55 of Ostwald's classics of exact sciences.C.G.J. Jacobi (1866) noted in his Vorlesungen über Dynamik (Lectures on Dynamics), in lecture 28 Die kürzeste Linie auf dem dreiachsigen Ellipsoid. Das Problem der Kartenprojektion (The shortest line on a three-axis ellipsoid. The problem of map projection), about Gauss's work the following: "It contains Lagrange's work, which is only slightly supplemented without being mentioned". In addition, Gauss only gave examples of the mapping of surfaces of rotation.
Jacobi dealt with the mapping of an ellipsoid with unequal axis to a plane in the aforementioned lectures. He gave the first hint of such solutions in 1839 in the Monatsberichten der Berliner Akademie and in the 19th volume of the Crelles Journala. The complete solution in addition to other tasks (mapping a surface of revolution, a cone, a cylinder into a plane) was communicated by Cohn based on Jacobi's legacy in the 59th volume of the Crelles Journala under the title Über die Abbildung eines ungleichachsigen Ellipsoides auf einer Ebene, bei welcher die kleinsten Teile änlich bleiben (On mapping an ellipsoid with unequal axis to a plane, whereby the smallest parts remain similar). This paper also contains a very simple theory of conformal mapping of one surface to another. In the lectures on dynamics, Jacobi explains: "Success in solving the problem of conformal mapping of an ellipsoid is achieved by appropriate substitution and a method that leads to one partial differential equation. The observed point of the ellipsoid will be determined by the intersection of two curvature curves." By dividing the surface of the ellipsoid into elements limited by curves of curvature, Legendre already determined this surface (Exercices du calcul integral, Exercises from the integral calculus, 1811) and in the process found the appropriate variables with which the well-known mapping task could be solved. Schering gave a complete solution to that task based on Jacobi's hints in the paper Über die konforme Abbildung des Ellipsoides auf der Ebene (On the conformal mapping of ellipsoids to the plane), for which he was awarded the prize of the Georgia Augusta Faculty of Philosophy in 1858.
In the environment of numerous works on cartography, most of which deal with the methods of construction of cartographic networks, one should certainly refer to the truly classic work, the cornerstone of the theory of map projections by TissotMémoire sur la représentation des surfaces et les projections des cartes géographiques (Discussion on the representation of surfaces and projections of geographical maps, Paris 1881,Figure 9) whose main part, chapters I to IV, appeared already between 1878 and 1880 in Nouvelles Annales de Mathématiques, 2e série. According to Zöppritz (1884), Tissot's work was noticed in Germany and Austria as well, and Hammer translated it into German under the titleDie Netzentwürfe geographischer Karten nebst Aufgaben über Abbildung beliebiger Flächen aufeinander from one arbitrary surface to another (Map projections of geographic maps with tasks on mapping one arbitrary surface to another, Stuttgart 1887), in which many views of cartographic grids and tables are added.
Figure 9.Tissot A (1881) Mémoire sur la représentation des surfaces et les projections des cartes géographiques − front page. / Slika 9.Tissot A (1881) Mémoire sur la représentation des surfaces et les projections des cartes géographiques − naslovnica

After 1900, about fifty monographs on map projections were published in a dozen languages. There are several of them in the English language that are very often quoted. In chronological order according to the first edition, they are suHinks (1912−21) Map projections,Deetz and Adams (1921−44) Elements of Map Projection,Steers (1927−70) An Introduction to the Study of Map Projections,Melluish (1931) An Introduction to the Mathematics of Map Projections,Richardus and Adler (1972) Map Projections for Geodesists, Cartographers and Geographers,Maling (1973−92) Coordinate Systems and Map Projections,Snyder (1982) Map Projections Used by the U. S. Geological Survey andSnyder (1987) Map Projections: A Working Manual andSnyder (1993) Flattening the Earth. There is also a manual byBugajevski and Snyder (1995) Map Projections − A Reference Manual. Longer discussions with special topics on map projections by Adams (1918−45),Young (1920),Thomas (1952),Lee (1976) andSnyder (1985) should certainly be mentioned.
In the German language, the following monographs should be highlighted:Maurer (1935) Ebene Kugelbilder,Wagner (1949, 1962) Kartographische Netzentwürfe,Merkel (1956, 1958) Grundzüge der Kartenprojektionslehre,Hoschek (1969, 1984) Mathematische Grundlagen der Kartographie,Kuntz (1983) Kartennetzentwurfslehre, then a series of works by the Bulgarian surveyor Hristov, published in the Zeitschrift für Vermessungswesen, i.e. in the form of books (1943,1955) and a German translation from the CzechFiala (1957) Mathematische Kartographie.
In French, the following stand out:Driencourt and Laborde (1932) Traité des projections des cartes géographiques teReignier (1957) Les systèms de projection et leurs applications.
Many monographs were written in the former Soviet Union, and the most prominent authors are:Kavrajskij (1958−60),Solov'ev (1946, 1969),Graur (1938, 1956),Urmajev (1941),Ginzburg and Salmanova (1957),Meščerjakov (1968), ,Pavlov (1974),Vahramejeva, Bugajevskij and Kazakova (1986). A book by the Bulgarian surveyorHristov (1957) was also published in Russian.
Today, geoinformation systems (GIS) enable some tasks that were once almost exclusively solved on maps (various cartometric tasks) to be solved directly from databases. Based on this fact, it could be concluded that geoinformation systems diminish the importance of geographic maps. If it is observed from the above point of view, then it is correct, but on the other hand, geographical maps are very important for every GIS. They play a very important role in the creation of databases, but also as a form of presentation of output data.
Since each map is made in a certain map projection, it can be concluded that map projections are particularly important when creating geoinformation systems. When creating national digital databases of geodetic, topographic and cartographic data, which must form the basis of any GIS that is done for the territory of the entire country, the digitization method of existing maps is important. That is why most GIS software also contains a digitization module. In the application of this module, it is necessary to know the map projection of the original and the constants of the projection (eg the longitude of the central meridian or the latitude of the standard parallel and the linear scales along them).
These data are necessary in order to transform the coordinates from the local system of the digitizer into the map projection system of the original and then, using the inverse equations of the map projection, into the geographic coordinate system. This makes it possible for the GIS software to offer a geographic map in one of the most important map projections as one of the forms of output data presentation. In order to draw such a map, it is necessary to calculate the rectangular coordinates x,y in the selected map projection from the geographic coordinates.
When creating software for any GIS, it is therefore necessary to know basic and inverse equations for a large number of map projections. Thus, computer-supported methods in the production of maps and especially geoinformation systems did not diminish, but rather increased, the importance of map projections. More than 1,000 papers on map projections published after 1960 and registered in the bibliography ofSnyder and Steward (1988) testify that this statement is correct.
3. Historical Development of Map Projections in Croatia
There is no comprehensive historical account of map projections and the people who dealt with their theory on the territory of Croatia. Croatian greats bear witness to the scientific tradition in Croats that goes back to the 12th century. Some of them made such contributions to science that their achievements mean new stages in the development of science. These are, for example, Herman Dalmatin in the 12th century and Josip Ruđer Bošković in the 18th century (Figure 10), who can be considered the forerunners of Croatian geodesy and cartography.
Figure 10. Map of the Papal State by J. R. Bošković and Ch. Maire from 1755. / Slika 10. Karta Papinske države J. R. Boškovića i Ch. Mairea iz 1755. godine
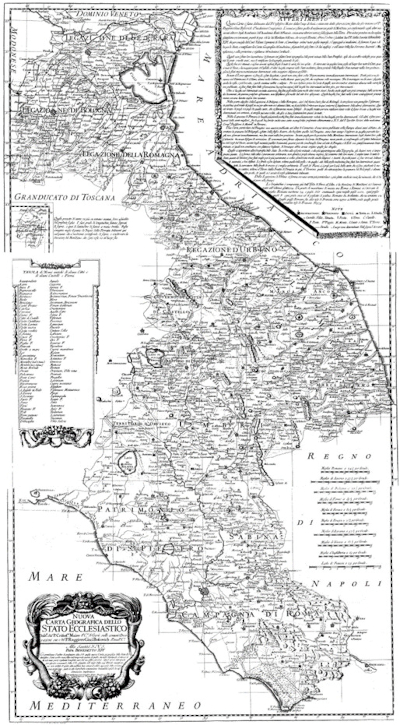
During the 19th and early 20th centuries, cadastral surveys were carried out on the territory of Croatia and plans were made in several coordinate systems. We call all these systems old. As the plans created in these systems were in use, the need arose to establish a connection between these systems and the Gauss-Krüger projection system. The old survey was carried out by experts under the leadership of institutions whose headquarters were in the administrative centers of the administrations of the time (Vienna, Budapest), so that very little data has been preserved to date, from which it would be possible to see how these works were carried out. The old coordinate systems in Croatia are: Kloštar-Ivanički, Budapest, Viennese, Krim and oblique conformal cylindrical projection. Insights into the origin of old systems and their characteristics are covered in several articles (Filkuka 1922,Sirks 1936,Čubranić 1947,Borčić 1954), and the bookTechnische Anleitung zur Ausführung der trigonometrischen Operationen des Katasters from 1875 by J. Marek is particularly important.
B. Borčić and N. Frančula worked with colleagues on the topic of Determining the elements of mutual transformation between projections and coordinate systems of the old and new land survey in the territory of SRH in the period 1962-66. The basic results of extensive research were published in the publication Old coordinate systems in the territory of SR Croatia and their transformation into Gauss-Krüger projection systems (Borčić, Frančula 1969). Later, Frančula specially treated the double oblique conformal cylindrical projection (Frančula 1972).
Although important research was carried out on map projections on Croatian territory in the 19th and early 20th centuries, it seems that there is still material that should be studied. For example, these are Mittheilungen des k. k. Militär-Geographischen Institutes which were published in Vienna, and in which, among other things, Hartl's relatively comprehensive articles on map projections (1886,1896) were published.
David Segen received his PhD at the Faculty of Philosophy in Zagreb in 1889 as the first PhD in the field of mathematics at the University of Zagreb. There he then teaches a series of courses, among which is Perspektivne mrežotine kartografijske (Cartographic networks of perspective) He wrote an extensive article entitledOn drawing networks for geographical maps, which was published in Izviešće o Kr. velikoj realci u Osieku at the end of the school year 1880/1. In addition, in 1893, he published an article in Nastavni vjesnik entitledOsnove reljef perspektive (Basics of perspective of relief).
Marije Kiseljak taught Mathematical Theory of Cartography (1922−23) and Cartography (1923−25) at the then Geodetic and Engineering Department of the Technical University in Zagreb.
Since November 1945, Vladimir Vranić has been working at the Geodetic Department of the Technical Faculty as a professor of Mathematical Cartography. Important for the history of map projections is his paperOn the derivation of the formulas of spherical trigonometry with the help of stereographic projection (1927), translated into German Über die Ableitung der Formeln der spärischen Trigonometrie mit Hilfe der stereographischen Projektion (1928).
Željko Marković (1889−1974) led mathematics at the Technical Faculty in Zagreb for many years. He did not teach cartography, but it is important that in his Higher Mathematics textbooks he treated conformal mappings in great detail, with special reference to conformal mappings of a sphere and ellipsoid in cartography (Marković 1965).
Regarding the history of map projections, it is good to note that all generations of mathematics students who took the Complex Analysis course were familiar with stereographic projection and conformal mapping. Namely, if the space of complex numbers is to be compactified, one infinitely distant element is added to it, and this can be done and clearly displayed by using stereographic projection. Conformal mappings are an integral part of Complex Analysis, the only question is whether to approach them abstractly, as Kurepa and Kraljević (1986) do, or concretely with examples from cartography (Marković 1965).
We should also mention that Vilko Niče in hisPerspective, which has seen several editions since 1953, deals with perspective projection of the sphere, among other things, and in the chapter on applications of central projection, he elaborates on stereographic and gnomonic projection.
Tomo Jakić (1879−1966) from Požega was a professor of mathematics and physics at grammar schools in Požega and Zagreb. In Nastavni vjesnik, which was published in Zagreb in 1916 for the 24th year, he published a very extensive article entitled Drawing networks for geographic maps . The article was published in four installments with a total of 52 pages.
Artur Franović-Gavazzi (1861−1944) was the most prominent physical geographer in Croatia at the turn of the century. Important for the history of map projections is his 66-page booklet entitled Kartografijske projekcije (Cartographic Projections), which, along with other manuscripts of his lectures at the University, was reproduced and published by the Academic Geographical Club in Zagreb (Gavazzi 1933).
In the 20th century, a number of geodetic experts worked in Croatia, for whom map projections were not their main area of interest, but they still left a written mark in that part of cartography. We list them in chronological order:V. Filkuka (Projections of land surveying in Croatia and Slavonia, 1922),N. P. Abakumov et al. (Projection of cadastral survey in the Kingdom of SHS, 1928-29), N. Čubranić ( Projection systems in Croatia, 1947, Table for length reduction in Gauss Krüger projection, 1948),E. Adamik (Reduction of direction and length in Gauss-Krüger projection, 1949),L. Randić (On the construction of verticals in stereographic projection, 1953),M. Bolt (Transformation of coordinates between adjacent coordinate systems of Gauss Krüger projections, 1974),Z. Narobe (Simplified way of calculating the convergence of the meridian for the needs of gyroscopic orientation, 1975),R. Solarić (Calculation of coordinates of points in the Mercator projection using a pocket computer, 1980) andM. Cigić (Transformation of coordinates from systems of the old measurement into systems of Gauss Krüger projection and vice versa, using a pocket computer, 1981).
Croatia became a member of the International Cartographic Association (ICA) in Barcelona in 1995, where the first national report for the period 1991−1995 was submitted. Reports were also submitted for 1995–1999 in Ottawa, for 1999–2003 in Durban, for 2003–2007 in Moscow, for 2007–2011 in Paris, for 2011–2015 in Rio de Janeiro, for 2015–2019 in Tokyo and for 2019−2023 in Cape Town. The Republic of Croatia has a complete overview of its cartographic activities over the past 32 years. All national reports are published on the ICA website and in the Cartography and Geoinformation journal. M. Lapaine was the chairman of the ICA Committee of Map Projections in the period 2011−2019.
4. Official Map Projections in Croatia
One of the basic issues of official cartography is the choice of the state projection, that is, the choice of the state coordinate system. Such a choice was relevant at the beginning of the 20th century, then with the creation of the Independent State of Croatia and the creation of the modern Republic of Croatia.
The question of the choice of projection and coordinate systems was raised in 1921. The then director of the cadastre entrusted the elaboration of this problem to a well-known geodetic scientist, professor A. Fasching, who came to Zagreb from Budapest. How complex a job it was, can be seen very well from the literature (Savezna geodetska uprava, 1953).
As soon as we talk about map projections, Jordan's famous saying comes to mind for all experts: "No institution penetrates so deeply into the essence of the entire survey and mapping of a country, as the choice of projection and coordinate system. If a mistake is made here, it will haunt many generations". According toAbakumovu (1946), in Croatia we felt these prophetic words to the full extent right on our own skin. We inherited several coordinate systems from the former Austro-Hungarian Monarchy. Abakumov wrote about the issue of choosing the most suitable projection for the Independent State of Croatia in 1942 and considered two variants of the Gauss-Krüger projection, their advantages and disadvantages.
The Gauss-Krüger projection is widely used in geodetic practice (Frančula 1974). In many European countries, this projection has been adopted as the official state projection. It is known that it was chosen as early as 1924 for the territory of the former Yugoslavia and that the rectangular coordinates of the state triangulation points were calculated and displayed in that projection. Considering the new circumstances, and especially regarding the shape of the Republic of Croatia, it was necessary to investigate the most favorable projection. The scientific and professional project Selection of state map projection was proposed to the State Geodetic Administration in 1994, 1995, 1997 and 1998.
At the end of 1999, the State Geodetic Administration of the Republic of Croatia recognized the problem of the mathematical basis of official cartography and ordered the preparation of the project "Proposal of official map projections of the Republic of Croatia" from the Faculty of Geodesy of the University of Zagreb. Based on the conducted tests, taking into account the analysis of the existing map projections in the Republic of Croatia, taking into account the recommendations and experiences of international bodies and associations, taking into account the national interests and the needs for defining the geodetic spatial system of the Republic of Croatia, the following official map projections are proposed:
Table 1. Proposal of official map projections of the Republic of Croatia
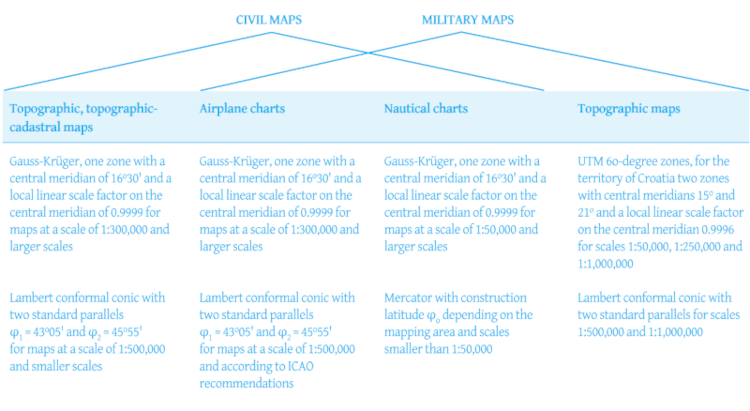
On the basis of the Law on the State Survey and Cadastre of Real Estate (Narodne novine, No. 128/99), the Government of the Republic of Croatia, at its session held on August 4, 2004, adopted the Decision on establishing the official geodetic datums and map projections of the Republic of Croatia. According to that Decision:
The coordinate system of the transverse Mercator (Gauss-Krüger) projection – abbreviated HTRS96/TM, with the central meridian 16°30' and the local linear scale factor on the central meridian 0.9999 is determined by the projection coordinate system of the Republic of Croatia for the area of the cadastre and detailed state topographic cartography.
The coordinate system of the normal aspect Lambert conformal conic projection – abbreviated HTRS96/LCC, with standard parallels 43°05' and 45°55' is determined by the projection coordinate system of the Republic of Croatia for the area of overview state cartography.
Coordinate systems of map projections are based on the Croatian terrestrial reference system.
For the needs of the Armed Forces of the Republic of Croatia, the projection coordinate system of the Universal Transverse Mercator projection (UTM) is adopted in accordance with the Standardization Agreement STANAG 2211, NATO member state, 5th edition of July 15, 1991.
5. Map Projections in Croatian Education
In general, almost nothing is taught about map projections in Croatian secondary schools, and relatively little in secondary schools for the education of geodetic technicians. These are: Geodetic Technical School in Zagreb, Civil Engineering and Geodetic School in Osijek, Cvilc Engineering Technical School in Rijeka, Technical School in Pula, Civil Engineering and Geodetic Technical School in Split, A. M. Reljković High School in Slavonski Brod, Craft and Technical School in Dubrovnik and Civil Engineering School in Čakovec.
The Institute of Cartography of the Faculty of Geodesy of the University of Zagreb was founded by an act of the University of Zagreb on May 22, 1956 at the Geodesy Department of the then Technical Faculty. The establishment of the Institute of Cartography was preceded by the establishment of the Chair of Cartography in 1951 after the election of Branko Borčić as an associate professor, i.e. the gradual formation of the Cartographic Laboratory, which was started by Ivan Kreiziger as early as 1948. Considerable teaching activity in the field of cartography existed even before the establishment of the Chair of Cartography. However, since its establishment, and especially since the establishment of the Institute of Cartography, significant scientific and professional activity has developed.
At today's Faculty of Geodesy of the University of Zagreb, there is a long-term continuity in the teaching of map projections and geodetic drawing. Professors Marije Kiseljak, PhD, Vladimir Vranić, PhD, Anton Fasching, PhD, Nikolaj P. Abakumov, Franjo Braum, PhD, Mato Janković, Branko Borčić, PhD, Nedjeljko Frančula, PhD, and Miljenko Lapaine, PhD, taught about map projections.
Stjepan Horvat (1895−1985) taught geodetic cartography in the 30s of the 20th century as part of the course State surveying. Until recently, very little was known about him because he was forced to emigrate after the Second World War. For the history of map projections, his works are very important both in terms of content and scope. If only his works in the field of geodesy and cartography were to be counted, the number would be more than hundreds, with a total of more than 2,000 pages.
Antal (Antun, Anton) Fasching (1879−1931) was one of the most educated Hungarian surveyors. He published about 70 works. In Zagreb, he taught Higher Geodesy, Cartography, State Surveying and Photogrammetry in the period from 1923 to 1928. In addition to his teaching work, his scientific work is also very important for the theory of map projections, primarily on solving the issue of choosing a state projection.
Nikolaj Pavlovič Abakumov (1882−1965) was elected in 1927 as a full professor at the Geodetic Department of the Technical Faculty in Zagreb, where he taught State Surveying, Higher Geodesy, Spherical Astronomy, Practical Astronomy, Applied Astronomy, Positional Astronomy, Photogrammetry, Cartography, Mathematical cartography, Applied cartography and Geophysics. Let us mention that Borčić, writing his textbook Mathematical Cartography, cited in the list of literature and lectures by Professor Abakumov at the Technical Faculty in Zagreb.
Branko Borčić (1908−1977) received his doctorate in 1964 at the Faculty of Architecture, Civil Engineering and Geodesy in Ljubljana with the thesisMathematical basis of the world map on a scale of 1:1,000,000. Since 1951, he has been an associate professor at the Technical Faculty in Zagreb, where he obtained his habilitation in 1956 with the work Contribution to the solution of coordinate transformation between adjacent coordinate systems in the Gauss-Krüger projection. Since 1960, he has been a full-time professor at the Faculty of Architecture, Civil Engineering and Geodesy in Zagreb. He wrote about issues of mathematical and geodetic cartography and published in Geodetskom glasnik (1939-40), Geodetska služba (1951), Geodetski list (1955, 1960, 1975), Građevinar (1958). His textbooks on map projections and Gauss-Krüger projection were used for years as the only manuals of their kind in Croatia (Figure 11).
Figure 11.Borčić B (1976) Gauss-Krügerova projekcija meridijanskih zona – front page / Slika 11.Borčić B (1976) Gauss-Krügerova projekcija meridijanskih zona − naslovnica

Nedjeljko Frančula graduated in 1962 from the Surveying Department of the Faculty of Architecture, Civil Engineering and Surveying in Zagreb. He received his doctorate in 1971 in Bonn (Landwirtschaftliche Fakultät) with the thesisDie vorteilhaftesten Abbildungen in der Atlaskartographie. In his doctoral dissertation, Frančula investigated the projections that would be best for making world maps. In doing so, he proposed 14 new projections, which, according to him, were named Frančula I−XIV (Jung 2021,Figure 12). In 1996, he was elected to the permanent position of full professor in technical sciences − the field of geodesy at the Faculty of Geodesy, University of Zagreb. In addition to Zagreb, he taught at undergraduate and postgraduate studies at the Faculty of Architecture, Civil Engineering and Geodesy in Ljubljana in 1974–76. The Senate of the University of Zagreb appointed him professor emeritus in 2007, and in 2008 he was declared an emeritus member of the Croatian Academy of Engineering. In 2013, the Croatian Geodetic Society awarded him the Golden Globe Lifetime Achievement Award.
Figure 12. World map in the Frančula XIII projection / Slika 12. Karta svijeta u projekciji Frančula XIII
Miljenko Lapaine graduated from the Faculty of Science and Mathematics of the University of Zagreb in the field of theoretical mathematics. He became a Doctor of Technical Sciences at the Faculty of Geodesy of the University of Zagreb by defending his dissertationMapping in the Theory of Map Projections .. He has been a professor emeritus since 2018. He published more than 1000 papers including several books. He participated as a representative of Croatia at all international cartographic conferences organized by the International Cartographic Association (ICA) from 1989 to 2019. Thanks to him, Croatia became a full member of the ICA in 1995. Miljenko Lapaine was elected an Honorary Fellow of the ICA in recognition of his many outstanding contributions to the ICA and his exceptional promotion of cartography at the international level. He is the president of the Croatian Cartographic Society and the executive editor of the Cartography and Geoinformation journal.
6. Conclusion
Map projections represent a special branch of cartography. They can be divided in various ways. The basic problem of the theory of map projections is that a spherical or ellipsoidal surface cannot be mapped onto a plane without distortion. The historical development of map projections begins several hundred years BC, and continues to this day. Map projections had and still have their application in Croatia. The article investigates and presents official map projections in Croatia and map projections in Croatian education.
1. Uvod
Kartografske projekcije su preslikavanja zakrivljene plohe, posebno elipsoida ili sfere, u ravninu (Lapaine 2017). Najčešće se zadaju analitički osnovnim kartografskim jednadžbama x=x(φ,λ), y=y(φ,λ) , gdje su φ,λ geografske ili geodetske koordinate, a x, y koordinate u ravnini projekcije. Mogu se zadati i tablicom koordinata ili opisom konstrukcije kartografske mreže (Frančula 2004).
Iako se zovu projekcije, ne treba ih poistovjećivati s projekcijama u matematici. Zapravo je riječ o preslikavanjima zakrivljene plohe u ravninu. Kartografske projekcije mogu se svrstati u nekoliko klasa ili skupina prema različitim kriterijima.
Po svojstvima preslikavanja dijele se na konformne, ekvivalentne, ekvidistantne i uvjetne projekcije. Po položaju osi projekcije dijele se na uspravne, poprečne i kose projekcije. Po obliku mreže pseudomeridijana i pseudoparalela dijele se na konusne, cilindrične, azimutne, pseudokonusne, pseudocilindrične, pseudoazimutne, polikonusne, kružne i ostale projekcije (Lapaine, Frančula 2022).
Kartografske projekcije često nose ime svojeg autora, npr. Mercatorova, Winkelova trostruka, Robinsonova. Kao posebna skupina kartografskih projekcija često se izdvajaju geodetske projekcije, tj. projekcije za potrebe državne izmjere.
Kartografske projekcije su neophodne jer je Zemlja približno sfernog oblika koji nije moguće preslikati u ravninu bez deformacija. Različite kartografske projekcije koriste se u različite svrhe, ovisno o željenoj razini točnosti i specifičnostima područja koje se kartira. Na primjer, kartografska projekcija koja je dobra za prikaz cijelog svijeta najčešće nije prikladna za prikaz detalja male regije, ni za prikaz kontinenata. Na primjer, ako iz karte svijeta izrađene u projekciji Eckert IV (slika 1a) izrežemo kartu Afrike (slika 1b), dobit ćemo nepotrebno izduženu sliku tog kontinenta. Ispravan odabir projekcije za kartu Afrike je primjerice azimutna ekvivalentna projekcija (slika 1c).
Primjena kartografskih projekcija omogućuje numeričko određivanje deformacija i njihovo isključivanje iz podataka preuzetih s karata. Deformacije karte su promjene duljina, površina, kutova i oblika koje proizlaze iz primjene kartografske projekcije.
Glavni problem u kartografiji je što nije moguće preslikati sfernu ili elipsoidnu površinu u ravninu bez deformacija (Lapaine 2023). Loše odabrana kartografska projekcija zapravo može biti štetna. Skloni smo vjerovati onome što vidimo, a kada su temeljni geografski odnosi, poput oblika, veličina i smjerova jako deformirani, skloni smo ih prihvatiti kao činjenicu ako ih tako vidimo na kartama. To može dovesti do vrlo pogrešnih dojmova. Na primjer, da je ruta New Yorka do Tokija prema istoku, ili da je Grenland po veličini samo nešto manji od Afrike iako je od nje oko 14 puta manji (slike2a i2b) Naše mentalne mape, geografska "baza podataka" mozga, generiraju se najvećim dijelom iz onoga što gledamo. Budući da globusi nisu uobičajeni, većina mentalnih slika Zemlje dolazi iz ravnih karata. Jako iskrivljen prikaz na karti koji se redovito vidi (kao što je ona na pozadini nekih televizijskih vijesti) nakon nekog vremena izgledat će poznato i stoga "izgledati ispravno". To može uzrokovati da se nečija mentalna karta svijeta trajno iskrivi. Budući da nijedna kartografska projekcija ne omogućava jedinstveno mjerilo na cijelom području, važno je odrediti u kojoj mjeri ono varira na karti. Primjerice, na karti svijeta, kvalitativna deformacija je očigledna oku upoznatom s kartama. Moguće je uočiti u kojoj su mjeri kopnene mase neprikladne veličine ili promijenjena oblika te u kojoj se mjeri meridijani i paralele ne sijeku pod pravim kutom ili nisu ravnomjerno raspoređeni. Na kartama zemalja ili čak kontinenata, deformacija možda neće biti vidljiva oku, ali postaje vidljiva nakon pažljivog mjerenja i analize.
Euler prvi je 1777. godine dokazao da ne postoji karta bez deformacija. Sve kartografske projekcije sadrže deformacije površina, kutova i/ili udaljenosti. Neke deformacije mogu se kontrolirati kako bi se sačuvale određene karakteristike, ali kartografske projekcije onda deformiraju druge karakteristike prikazanog objekta.
Klasičan način prikazivanja deformacija neke projekcije je upotreba Tissotovih indikatrisa ili elipsa deformacija.Tissot (1881) je opisao konstrukciju elipse koja lokalno prikazuje iznos i orijentaciju komponenti deformacija. Naime, svaka kartografska projekcija može se lokalno aproksimirati afinim preslikavanjem. Preslikavanjem kružnice infinitezimalno malog radijusa dobiva se elipsa koju nazivamo elipsom deformacija ili Tissotovom indikatrisom. Osi te elipse nazivaju se glavnim smjerovima i uzduž njih je lokalno linearno mjerilo najveće, odnosno najmanje. Tissotova indikatrisa često se koristi za ilustraciju varijacije mjerila na karti.
Jedna indikatrisa opisuje deformacije u jednoj točki. Budući da deformacije variraju na karti, općenito se Tissotove indikatrise postavljaju na više mjesta na karti kako bi se ilustrirala prostorna promjena deformacija. Uobičajena shema postavlja ih na svako sjecište prikazanih meridijana i paralela (slika 3). Te sheme su važne u proučavanju kartografskih projekcija, kako za ilustraciju raspodjele deformacija tako i za pružanje osnove za računanje veličine deformacija u svakoj točki.
Na kartama izrađenima u konformnim projekcijama Tissotove indikatrise su kružnice čija veličina varira ovisno o lokaciji. Na kartama izrađenima u ekvivalentnim projekcijama sve Tissotove indikatrise imaju istu površinu, iako se njihovi oblici i orijentacije razlikuju ovisno o lokaciji. U proizvoljnim projekcijama, i površina i oblik indikatrisa variraju na karti.
Sedamdesetih godina prošlog stoljeća Konusova je predložila lokalni kriterij. Taj kriterij je kutna vrijednost. Nazovimo ga kutom klasifikacije. Kut klasifikacije α računa se na sljedeći način:
gdje su a i b poluosi elipse deformacija. Razmotrimo tu formulu detaljnije. U konformnim projekcijama u bilo kojoj točki na karti linearno mjerilo ne ovisi o smjeru, a = b, pa je prema tome α=0. U ekvivalentnim projekcijama ab = 1, dakle, α=π/2. U ekvidistantnim projekcijama učinci deformacija oblika (kutova) i površina su isti; u formuli je brojnik jednak nazivniku, α=π/4. Stoga se kvantitativna procjena podjele projekcija prema prirodi deformacija na temelju vrijednosti kuta klasifikacije može provesti na sljedeći način:
In conformal projections at any point on the map, the linear scale does not depend on the direction a = b, so α=0. In equivalent projections, ab = 1, therefore, α=π/2. In equidistant projections, the effects of distortion of shapes (angles) and area are the same; in the formula, the numerator is equal to the denominator, α=π/4. Therefore, the quantitative assessment of the classification of projections according to the nature of the distorions based on the value of the classification angle can be carried out in the following way:
α=0 − konformne projekcije
α=π/4 − ekvidistantne projekcije
α=π/2 − ekvivalentne projekcije
Da bi se usporedile kartografske projekcije s obzirom na njihove karakteristike deformacija, prikladno je kvantificirati ukupnu deformaciju jednom jedinom mjerom. To nije tako jednostavno kao što se može činiti.Tissot (1881) je predložio karakterizirati deformaciju kartografske projekcije maksimalnom vrijednošću postignutom na kartiranom području. Maksimalne vrijednosti deformacija mogu se izračunati, ali imaju jedan veliki nedostatak. Ne uzima se u obzir kako je deformacija prostorno raspoređena. Da bi se uzele u obzir prostorne varijacije distorzije, lokalne mjere mogu se integrirati na području interesa. Poznati su kriteriji Jordana, Airyja, Airy-Kavrajskoga i drugih.
Važno je napomenuti da se sve deformacije mogu otkloniti ako znamo u kakvoj je kartografskoj projekciji karta izrađena. Kartografi obično žele izraditi kartu sa što manje deformacija. Međutim, u nekim slučajevima pristup je obrnut. Kartogram (također karta vrijednosnog područja ili anamorfna karta) je tematska karta na kojoj su udaljenosti u nekoj linijskoj mreži ili površine teritorijalnih, najčešće administrativnih, jedinica namjerno deformirane (Lapaine 2023).
Projekcija karte ključna je za navigaciju, posebno za mornare i pilote koji se koriste kartama za navigaciju. Loksodroma je krivulja na rotacijskoj plohi koja siječe meridijane pod jednakim kutom. Brod plovi po loksodromi kad na putu između dviju pozicija plovi stalno po istom kursu. U uspravnoj Mercatorovoj projekciji loksodrome su ravne crte. Ortodroma je geodetska linija na sferi i prema tome dio velike kružnice. Brod koji plovi po ortodromi prelazi najkraći put između dviju pozicija. Međutim, na karti izrađenoj u uspravnoj Mercatorovoj projekciji luk loksodrome između dviju točaka kraći je od luka ortodrome koja spaja te iste dvije točke.
Pri izražavanju problema koje razmatra i pri pronalaženju njihovih analitičkih rješenja, teorija kartografskih projekcija primjenjuje postavke mnogih matematičkih disciplina, kao što su ravna i sferna trigonometrija, diferencijalna geometrija, diferencijalni i integralni račun, metode numeričke analize itd. Podatke o obliku i veličini Zemlje i koordinatama točaka geodetske osnove te astronomskih točaka, teorija kartografskih projekcija preuzima iz geodezije i geodetske astronomije. Isto je tako jasno izražena obostrana povezanost teorije kartografskih projekcija s geografijom i drugim znanostima za čije se potrebe izrađuje velik broj raznovrsnih karata.
Osnovni su zadatci teorije kartografskih projekcija sljedeći:
širenje znanja o kartografskim projekcijama;
razvoj teorije kartografskih projekcija, ponajprije u području dobivanja najboljih kartografskih projekcija, uključujući "najbolje" i "idealne";
ispitivanje različitih kartografskih projekcija, njihove biti, svojstava, međuovisnosti i učinkovitosti primjene u praksi;
usavršavanje postojećih kartografskih projekcija i njihova normizacija;
istraživanje uloge kartografskih projekcija i njihove primjene u geoinformacijskim sustavima;
usavršavanje metoda istraživanja novih kartografskih projekcija, osobito algoritama i odgovarajućeg softvera uz poboljšanja tehnika računanja;
razrada drugih matematičkih elemenata karte kao što su mjerilo, podjela na listove itd., a pojavljuju se pri izdanjima na više listova;
ispitivanje i rješavanje zadataka matematičkog karaktera koji se pojavljuju pri sastavljanju karata (npr. transformiranje kartografskih projekcija primjenom različitih pomagala, uključujući računala);
razrada teorije i metoda automatizacije u primjeni kartografskih projekcija.
2. Povijesni razvoj kartografskih projekcija
Razvoj kartografskih projekcija tekao je usporedno s razvitkom izradbe karata i kartografije općenito. Razvoj mnogih znanosti, tehnička dostignuća i potrebe svakodnevnoga života s vremenom su inicirali sve šire zahtjeve za izradbom raznovrsnih topografskih i tematskih karata različitog mjerila i namjene, što je zahtijevalo neprekidno povećavanje broja kartografskih projekcija i usavršavanje matematičke osnove karata.
Počeci kartografskih projekcija stari su više od dvije tisuće godina, otkad su grčki znanstvenici prvi uveli matematičke principe u osnovu preslikavanja Zemlje i zvjezdanoga neba te počeli primjenjivati mrežu meridijana i paralela. Veliku su ulogu u razvoju kartografije odigrali radovi Anaksimandara, Eratostena, Apolonija i Hiparha (Snyder 1993).
Smatra se da je prvu kartu u nekoj projekciji izradio Tales iz Mileta 600. godine prije Krista. Bila je to karta nebeske sfere u gnomonskoj projekciji. Među najstarije se projekcije ubrajaju stereografska i ortografska koje je upotrijebio poznati grčki astronom i matematičar Hiparh, također za izradbu karata nebeske sfere oko 150. godine prije Krista. Od toga doba do danas izumljeno je nekoliko stotina kartografskih projekcija.U 2. st. Ptolemej je napisao kapitalno djelo Geografija u koje je uključio opis sastavljanja karata i određivanje Zemljinih dimenzija te konstrukciju kartografskih projekcija.
T i O karta ili O–T ili T–O karta (orbis terrarum, sa slovom T unutar O), također poznata kao Izidorova karta, vrsta je rane karte svijeta koja predstavlja svijet kako ga je prvi opisao učenjak iz 7. stoljeća Izidor Seviljski (oko 560.–636.) u svom djelu De Natura Rerum i kasnije u svojim Etymologiae (oko 625.). Naslici 4 prikazana je T i O karta, iz prve tiskane verzije Izidorove Etymologiae, na kojoj su označena tri poznata kontinenta.
Epohu srednjovjekovlja u Europi obilježila je pojava tzv. samostanskih karata, koje su odražavale religioznu predodžbu svijeta bez mreža koordinata i bez značaja kartografskih projekcija.
Osobit je razvoj kartografije započeo za renesanse − razdoblja velikih geografskih otkrića. Postale su nužne točne, pouzdane karte za upravljanje državom, za vojničke potrebe, za razvoj trgovine i pomorstva. Takve su karte mogle biti sastavljene samo primjenom matematičke osnove i rezultata izmjere zemljišta. Najprije su se pojavile topografske karte.
Krajem 16. i početkom 17. st. značajan je događaj u daljnjem razvoju i popularizaciji kartografije bio sastavljanje i izdavanje geografskih atlasa u izdanju poznatih nizozemskih kartografa Orteliusa i Mercatora. Mercator je prvi primijenio konformnu cilindričnu projekciju koja se do danas uspješno koristi za pomorske navigacijske karte.
Pri izradbi karata svijeta i teritorija većih dimenzija široku su primjenu tada imale trapezna projekcija i Apianova projekcija, koje su poslužile kao prauzori za kasnije razrađene pseudocilindrične projekcije. U 17. je stoljeću novu sinusnu pseudocilindričnu projekciju za kartu svijeta predložio francuski kartograf Sanson (slika 5).
Razrada znanstvene osnove kartografije i početak topografskog izučavanja Zemlje te kao rezultat toga daljnje povećanje točnosti i pouzdanosti karata obilježuju 18. stoljeće. U kartografsku je praksu uveden niz novih projekcija što su ih predložili Bonne (slika 6), Lambert, Lagrange, Euler i drugi.
Renesansa je završila uvođenjem elementarne matematičke analize u razvoj kartografskih projekcija. Takva je analiza posebno primijenjena na Mercatorovu projekciju u kojoj su loksodrome prikazane kao pravci i na projekcije u kojima su sve prikazane paralele podijeljene meridijanima na jednakom razmaku, bez obzira jesu li paralele kružni lukovi (Wernerova projekcija) ili pravci (sinusna). Kartografske projekcije postaju složenije: umjesto onih čije se kartografske mreže jednostavno crtaju jer se sastoje od kružnih lukova i pravaca, pojavljuju se takve koje se crtaju uz pomoć tablica trigonometrijskih funkcija.
Murdoch (1758) je svjesno postavio zahtjev da ukupna površina preslikanog područja bude korektna, ali nije ustrajao na konstantnosti lokalnog mjerila površina. Prvo namjerno očuvanje površinske vjernosti u svakoj točki učinio jeLambert (1772) pri svojem izumu cilindričnih, azimutnih i konusnih ekvivalentnih projekcija. Halley je geometrijski dokazao konformnost stereografske projekcije, a Lambert je to učinio diferencijalnim računom te izumio također tri nove konformne projekcije. Mnoge su kartografske projekcije nastale i u 19. i 20. stoljeću, ali su osnovni principi postavljeni do 1772. i osobito u toj godini.
Najznačajniji doprinos kartografa, geodeta i matematičara 19. stoljeća teoriji kartografskih projekcija bio je uspostavljanje čvrstih matematičkih principa. Lambert i Lagrange napravili su značajan početak 1770-ih, ali su naročito Gauss i Tissot dali velike doprinose do 1880-ih. Drugi istraživaći, kao Airy, Clarke, Schwartz i Peirce (slika 7) usredotočili su se na specifičnije, ali složenije zadatke, dok su Germain, Gretschel i Craig skupili različite radove drugih znanstvenika u posebne monografije. Nove projekcije Mollweidea, Albersa, Galla i drugih sadrže jednostavniju primjenu matematike, ali ipak zaslužuju nazive prema svojim izumiteljma. Ubrzani se razvoj teorije kartografskih projekcija u tom razdoblju uočava većim brojem novih projekcija i brojem objavljenih knjiga i članaka (Snyder 1993).
PremaFrischaufu (1905) početak teorije preslikavanja jedne plohe na drugu pripada Lambertu, koji se u Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten (Napomene i dopune zasnivanju karata zemljišta i neba) u trećem dijelu svojih Beyträge zum Gebrauch der Mathematik und deren Anwendung (Doprinosi uporabi matematike i njezine primjene, 1772,slika 8), bavio općenito postavljenom zadaćom preslikavanja sfere i sferoida u ravninu. Lambertov je kolega Lagrange bio nadahnut njegovim razdvajanjem varijabli u izrazu za diferencijal duljine luka pri konformnom preslikavanju te riješio problem konformnog preslikavanja rotacijskih ploha i objavio ga u dvije rasprave Sur la construction des cartes géographiques (O konstrukciji geografskih karata, Nouveaux Mémoires de l'Académie Royal de Berlin, 1779).
Početkom 19. st. vojne ustanove počele su izradu topografskih karata u krupnim mjerilima, za koje matematička osnova ima posebnu važnost jer su se na tim kartama određivale udaljenosti i smjerovi. Godine 1822. postavilo je Kraljevsko znanstveno društvo u Kopenhagenu nagradno pitanje: naći opće rješenje zadatka − dio zadane plohe preslikati na drugu zadanu plohu tako da slika bude u najmanjim dijelovima slična izvorniku. Za rješenje zadatka nagradu je dobio C. F. Gauss. Taj je rad najprije objavljen u Schumacherovim Astronomische Abhandlungen 1825. godine. Lagrangeova i Gaussova rasprava sadržane su u svesku broj 55 Ostwaldovih klasika egzaktnih znanosti.Jacobi (1866) je primijetio u svojim Vorlesungen über Dynamik (Predavanja o dinamici), u 28. predavanju Die kürzeste Linie auf dem dreiachsigen Ellipsoid. Das Problem der Kartenprojektion (Najkraća linija na troosnom elipsoidu. Problem kartografske projekcije), o Gaussovu radu sljedeće: "U njemu je sadržan Lagrangeov rad, koji je samo malo dopunjen, a da nije spomenut". Gauss je osim toga dao samo primjere preslikavanja rotacijskih ploha.
Preslikavanje raznoosnog elipsoida u ravninu obradio je u spomenutim predavanjima Jacobi. Prvi je nagovještaj takva rješenja dao 1839. u Monatsberichten der Berliner Akademie i u 19. svesku Crelles Journala. Potpuno rješenje uz druge zadatke (preslikavanje rotacijske plohe, stošca, valjka u ravninu) priopćio je Cohn na temelju Jacobijeve ostavštine u 59. svesku Crelles Journala pod naslovom Über die Abbildung eines ungleichachsigen Ellipsoides auf einer Ebene, bei welcher die kleinsten Teile änlich bleiben (O preslikavanju raznoosnog elipsoida u ravninu, pri čemu najmanji dijelovi ostaju slični). Taj rad sadrži također vrlo jednostavnu teoriju konformnog preslikavanja jedne plohe na drugu. U predavanjima o dinamici Jacobi objašnjava: "Uspjeh rješenja zadatka konformnog preslikavanja elipsoida postiže se odgovarajućom supstitucijom i metodom koja vodi na jednu parcijalnu diferencijalnu jednadžbu. Uočena točka elipsoida bit će određena presjekom dviju krivulja zakrivljenosti". Rastavljanjem plohe elipsoida na elemente ograničene krivuljama zakrivljenosti već je tu plohu odredio Legendre (Exercices du calcul integral, Vježbe iz integralnog računa, 1811) i pritom pronašao odgovarajuće varijable s pomoću kojih se poznati zadatak o preslikavanju mogao riješiti. Ernst Schering je dao potpuno rješenje tog zadatka na temelju Jacobijevih nagovještaja u radu Über die konforme Abbildung des Ellipsoides auf der Ebene (O konformnom preslikavanju elipsoida u ravninu) za koji je 1858. nagrađen nagradom Filozofskog fakulteta Georgia Augusta.
U okruženju mnogobrojnih radova o kartografiji, od kojih se većina bavi metodama konstrukcije kartografskih mreža, trebalo bi se svakako osvrnuti na zaista klasično djelo, kamen temeljac teorije kartografskih projekcija TissotaMémoire sur la représentation des surfaces et les projections des cartes géographiques (Rasprava o prikazivanju ploha i projekcijama geografskih karata, Pariz 1881,slika 9) čiji se osnovni dio, poglavlja I do IV, pojavio već izmđu 1878. i 1880. u Nouvelles Annales de Mathématiques, 2e série. Prema Zöppritzu (1884), Tissotov je rad bio zapažen i u Njemačkoj i Austriji, i Hammer ga je preveo na njemački pod naslovomDie Netzentwürfe geographischer Karten nebst Aufgaben über Abbildung beliebiger Flächen aufeinander (Prikazi kartografskih mreža geografskih karata uz zadatke o preslikavanju jedne proizvoljne plohe na drugu, Stuttgart 1887), u kojemu su pridodani mnogi prikazi kartografskih mreža i tablice.
Nakon 1900. objavljeno je pedesetak monografija o kartografskim projekcijama na desetak jezika. Na engleskom jeziku ima ih nekoliko koje se vrlo često citiraju. Kronološkim redoslijedom prema prvome izdanju to suHinks (1912−21) Map projections,Deetz i Adams (1921−44) Elements of Map Projection,Steers (1927−70) An Introduction to the Study of Map Projections,Melluish (1931) An Introduction to the Mathematics of Map Projections,Richardus i Adler (1972) Map Projections for Geodesists, Cartographers and Geographers,Maling (1973−92) Coordinate Systems and Map Projections,Snyder (1982) Map Projections Used by the U. S. Geological Survey iSnyder (1987) Map Projections: A Working Manual. Tu je i priručnikBugajevskoga i Snydera (1995) Map Projections − A Reference Manual. Svakako treba spomenuti i dulje rasprave s posebnim temama o kartografskim projekcijama Adamsa (1918−45),Younga (1920),Thomasa (1952),Leeja (1976) iSnydera (1985).
Na njemačkom jeziku treba istaknuti sljedeće monografije:Maurer (1935) Ebene Kugelbilder,Wagner (1949, 1962) Kartographische Netzentwürfe,Merkel (1956, 1958) Grundzüge der Kartenprojektionslehre,Hoschek (1969, 1984) Mathematische Grundlagen der Kartographie,Kuntz (1983) Kartennetzentwurfslehre, zatim niz radova bugarskoga geodeta Hristova, objavljenih u Zeitschrift für Vermessungswesen, odnosno u obliku knjiga (1943,1955) i njemački prijevod s češkogFiala (1957) Mathematische Kartographie.
Na francuskom se jeziku ističu:Driencourt i Laborde (1932) Traité des projections des cartes géographiques teReignier (1957) Les systèms de projection et leurs applications.
U bivšem je Sovjetskom Savezu napisano mnogo monografija, a najistaknutiji autori su:Kavrajskij (1958−60),Solov'ev (1946, 1969),Graur (1938, 1956),Urmajev (1941),Ginzburg i Salmanova (1957),Meščerjakov (1968), ,Pavlov (1974),Vahramejeva, Bugajevskij i Kazakova (1986). Na ruskom je jeziku objavljena također knjiga bugarskoga geodetaHristova (1957).
Danas geoinformacijski sustavi (GIS) omogućuju da se neki zadatci koji su se nekada gotovo isključivo rješavali na kartama (razni kartometrijski zadaci) sada rješavaju izravno iz baza podataka. Na temelju te činjenice moglo bi se zaključiti da geoinformacijski sustavi umanjuju važnost geografskih karata. Ako se to promatra s navedenog stajališta, onda i jest točno, no s druge su strane geografske karte vrlo važne za svaki GIS. One imaju vrlo važnu ulogu pri stvaranju baza podataka, ali i kao jedan od oblika prezentacije izlaznih podataka.
Budući da se svaka karta izrađuje u određenoj kartografskoj projekciji, može se zaključiti da su kartografske projekcije osobito važne pri stvaranju geoinformacijskih sustava. Pri stvaranju nacionalnih digitalnih baza geodetskih, topografskih i kartografskih podataka, koje moraju činiti temelj svakoga GIS-a što se radi za područje čitave države, važna je metoda digitalizacije postojećih karata. Zbog toga većina GIS-softvera sadrži i modul za digitalizaciju. U primjeni tog modula nužno je poznavati kartografsku projekciju izvornika i konstante projekcije (npr. geografsku dužinu srednjeg meridijana ili širinu standardne paralele i linearna mjerila uduž njih).
Ti su podatci nužni da bi se koordinate iz lokalnog sustava digitalizatora transformirale u sustav kartografske projekcije izvornika i potom pomoću inverznih jednadžbi kartografske projekcije u sustav geografskih koordinata. Time je omogućeno da GIS-softver kao jedan od oblika prezentacije izlaznih podataka nudi geografsku kartu u nekoj od većeg broja najvažnijih kartografskih projekcija. Da bi se takva karta nacrtala, nužno je iz geografskih koordinata izračunati pravokutne koordinate x, y u izabranoj kartografskoj projekciji.
Pri izradi softvera za bilo koji GIS potrebno je, prema tome, poznavati osnovne i inverzne jednadžbe za veći broj kartografskih projekcija. Dakle, računalno podržane metode u izradbi karata i poglavito geoinformacijski sustavi nisu umanjili, nego su povećali važnost kartografskih projekcija. Da je ta tvrdnja točna svjedoči više od 1000 radova o kartografskim projekcijama objavljenih nakon 1960, a registriranih u bibliografijiSnydera i Stewarda (1988).
3. Povijesni razvoj kartografskih projekcija u Hrvatskoj
Sveobuhvatni povijesni prikaz o kartografskim projekcijama i osobama koje su se bavile njihovom teorijom na tlu Hrvatske ne postoji. Hrvatski velikani svjedoče o znanstvenoj tradiciji u Hrvata koja seže u 12. stoljeće. Neki su od njih dali takve doprinose znanosti da njihova dostignuća znače nove etape u razvoju znanosti. To su primjerice Herman Dalmatin u 12. stoljeću i Josip Ruđer Bošković (slika 10) u 18. stoljeću koje možemo smatrati pretečama hrvatske geodezije i kartografije.
Tijekom 19. i početkom 20. stoljeća izvodila se na području Hrvatske katastarska izmjera i izrađeni su planovi u nekoliko koordinatnih sustava. Sve te sustave nazivamo starima. Kako su planovi izrađeni u tim sustavima bili u uporabi, pojavila se potreba za uspostavom veze između tih sustava i sustava Gauss-Krügerove projekcije. Staru su izmjeru izvodili stručnjaci pod vodstvom ustanova čija su sjedišta bila u administrativnim centrima tadašnjih uprava (Beč, Budimpešta), tako da je do danas očuvano vrlo malo podataka iz kojih bi se moglo vidjeti kako su ti radovi izvođeni. Stari koordinatni sustavi na području Hrvatske su: Kloštar-Ivanički, Budimpeštanski, Bečki, Krimski i kosa konformna cilindrična projekcija. Uvid u postanak starih sustava i njihove karakteristike obrađeni su u nekoliko članaka (Filkuka 1922,Sirks 1936,Čubranić 1947,Borčić 1954), a osobito je važna knjiga J. MarekaTechnische Anleitung zur Ausführung der trigonometrischen Operationen des Katasters iz 1875.
B. Borčić i N. Frančula radili su sa suradnicima na temi Odrediti elemente međusobne transformacije između projekcija i koordinatnih sustava stare i nove izmjere zemljišta na području SRH u razdoblju 1962−66. Osnovni rezultati provedenih opsežnih istraživanja objavljeni su u publikaciji Stari koordinatni sustavi na području SR Hrvatske i njihova transformacija u sustave Gauss-Krügerove projekcije (Borčić, Frančula 1969). Poslije je Frančula posebno obradio dvostruku kosu konformnu cilindričnu projekciju (Frančula 1972).
Premda su provedena važna istraživanja o kartografskim projekcijama na tlu Hrvatske u 19. i početkom 20. stoljeća, čini se da ima još materijala koji bi trebalo proučiti. Na primjer, to su Mittheilungen des k. k. Militär-Geographischen Institutes što su izlazili u Beču, a u kojima su među ostalim objavljeni i relativno opsežni članci H. Hartla o kartografskim projekcijama (1886,1896).
David Segen doktorirao je na Mudroslovnom fakultetu u Zagrebu 1889. kao prvi doktor iz područja matematike na zagrebačkom Sveučilištu. Tu potom predaje niz kolegija, među kojima i Perspektivne mrežotine kartografijske. Napisao je opsežan članak pod naslovomO crtanju mreža za geografijske karte, što je objavljen u Izviešću o Kr. velikoj realci u Osieku koncem šk. god. 1880/1. Osim toga objavio je 1893. u Nastavnom vjesniku članak pod naslovomOsnove reljef perspektive.
Marije Kiseljak je predavao Matematičku teoriju kartografije (1922−23) i Kartografiju (1923−25) na tadašnjem Geodetsko-inženjerskom odjelu Tehničke visoke škole u Zagrebu.
Vladimir Vranić od studenoga 1945. radi na Geodetskom odjelu Tehničkog fakulteta kao profesor Matematičke kartografije. Za povijest kartografskih projekcija važan je njegov radO izvođenju formula sferne trigonometrije s pomoću stereografske projekcije (1927), u prijevodu na njemački Über die Ableitung der Formeln der spärischen Trigonometrie mit Hilfe der stereographischen Projektion (1928).
Željko Marković (1889−1974) predvodio je dugo godina matematiku na Tehničkom fakultetu u Zagrebu. Nije predavao kartografiju, ali je važno da je u svojim udžbenicima iz Više matematike vrlo detaljno obradio konformna preslikavanja, s posebnim osvrtom na konformna preslikavanja sfere i elipsoida u kartografiji (Marković 1965).
Za povijest kartografskih projekcija dobro je zabilježiti i to da su svi naraštaji studenata matematike koji su slušali kolegij Kompleksna analiza upoznati sa stereografskom projekcijom i konformnim preslikavanjima. Naime, želi li se prostor kompleksnih brojeva kompaktificirati, dodaje mu se jedan beskonačno daleki element, a to se može učiniti i zorno prikazati s pomoću stereografske projekcije. Konformna su preslikavanja sastavni dio Kompleksne analize, pitanje je samo pristupiti li im apstraktno, kao što rade primjerice Kurepa i Kraljević (1986), ili konkretno s primjerima iz kartografije (Marković 1965).
Spomenimo također da Vilko Niče u svojojPerspektivi, koja je od 1953. doživjela nekoliko izdanja, obrađuje među ostalim i perspektivnu projekciju kugle, a u poglavlju o primjenama centralne projekcije obrađuje stereografsku i gnomonsku projekciju.
Tomo Jakić (1879−1966) iz Požege bio je profesor matematike i fizike na gimnazijama u Požegi i Zagrebu. U Nastavnom vjesniku, koji 1916. izlazi u Zagrebu već 24. godište, objavio je vrlo opsežan članak pod naslovomCrtanje mreža za geografske karte. Članak je izašao u četiri nastavka na ukupno 52 stranice.
AArtur Franović-Gavazzi (1861−1944) najistaknutiji je fizički geograf u Hrvatskoj na prijelazu stoljeća. Za povijest kartografskih projekcija važna je njegova knjižica od 66 stranica pod naslovom Kartografijske projekcije, koju je uz druge rukopise njegovih predavanja na Sveučilištu umnožio i izdao Akademski geografski klub u Zagrebu (Gavazzi 1933).
U 20. je stoljeću u Hrvatskoj djelovao niz geodetskih stručnjaka kojima kartografske projekcije nisu bile osnovno područje zanimanja, ali su ipak ostavili pisani trag i u tom dijelu kartografije. Navodimo ih kronološkim redoslijedom:V. Filkuka (Projekcije zemaljske izmjere u Hrvatskoj i Slavoniji, 1922),N. P. Abakumov i dr. (Projekcija katastarskog premera u Kraljevini SHS, 1928-29), N. Čubranić (Projekcioni sistemi u Hrvatskoj, 1947,Tablica za redukciju dužina kod Gauss Krügerove projekcije, 1948),E. Adamik (Redukcija smjera i dužine u Gauss-Krügerovoj projekciji, 1949),L. Randić (O konstrukciji vertikala u stereografskoj projekciji, 1953),M. Bolt (Transformacija koordinata između susjednih koordinatnih sistema Gauss Krügerove projekcije, 1974),Z. Narobe (Pojednostavljen način računanja konvergencije meridijana za potrebe žiroskopske orijentacije, 1975),R. Solarić (Računanje koordinata točaka u Mercatorovoj projekciji primjenom džepnog računala, 1980) iM. Cigić (Transformacija koordinata iz sustava stare izmjere u sustave Gauss Krügerove projekcije i obrnuto, primjenom džepnog računala, 1981).
Hrvatska je postala članicom Međunarodnoga kartografskog društva (International Cartographic Association – ICA) u Barceloni 1995. godine, gdje je podnijela svoj prvi nacionalni izvještaj za razdoblje 1991–1995. Podneseni su izvještaji i za 1995–1999. u Ottawi, za 1999–2003. u Durbanu, za 2003–2007. u Moskvi, za 2007–2011. u Parizu, za 2011–2015. u Rio de Janeiru, za 2015–2019. u Tokiju i za 2019−2023. u Cape Townu. Republika Hrvatska ima cjelovit pregled svojih kartografskih aktivnosti u protekle 32 godine. Svi nacionalni izvještaji objavljeni su na web-stranicama ICA-e i u časopisu Kartografija i geoinformacije. M. Lapaine bio je predsjedavajući Povjerenstva za kartografske projekcije ICA-e u razdoblju 2011−2019.
4. Službene kartografske projekcije u Hrvatskoj
Jedno je od osnovnih pitanja službene kartografije izbor državne projekcije, odnosno izbor državnog koordinatnog sustava. Takav je izbor bio aktualan početkom 20. stoljeća, zatim stvaranjem Nezavisne Države Hrvatske i stvaranjem suvremene Republike Hrvatske.
Pitanje izbora projekcije i koordinatnih sustava bilo je pokrenuto 1921. godine. Tadašnji je direktor katastra povjerio razradu tog problema poznatom geodetskom znanstveniku, profesoru A. Faschingu, koji je u Zagreb došao iz Budimpešte. Koliko je to bio složen posao, vrlo dobro se može vidjeti iz literature (Savezna geodetska uprava, 1953).
Čim se povede govor o kartografskim projekcijama, nehotice dolazi u sjećanje svim stručnjacima poznata izreka Jordana: "Ni jedna ustanova ne zadire tako duboko u suštinu cjelokupne izmjere i kartiranja jedne zemlje, kao izbor projekcije i koordinatnog sistema. Ako se ovdje načini pogreška ta se sveti na mnogim generacijama". PremaAbakumovu (1946), u Hrvatskoj smo te proročanske riječi osjetili u punoj mjeri baš na svojoj koži. Od bivše Austro-Ugarske Monarhije naslijedili smo nekoliko koordinatnih sustava. O pitanju izbora najprikladnije projekcije za Nezavisnu Državu Hrvatsku pisao jeAbakumov 1942. i razmatrao dvije varijante Gauss-Krügerove projekcije, njihove prednosti i nedostatke.
Gauss-Krügerova projekcija ima vrlo široku primjenu u geodetskoj praksi (Frančula 1974). U mnogim je europskim državama ta projekcija usvojena kao službena državna projekcija. Poznato je da je ona izabrana još 1924. godine za područje bivše Jugoslavije i da su se pravokutne koordinate točaka državne triangulacije računale i prikazivale u toj projekciji. S obzirom na nove okolnosti, a napose u pogledu oblika Republike Hrvatske i njezina protezanja, bilo je potrebno istražiti najpovoljniju projekciju. Državnoj geodetskoj upravi predložen je znanstveno-stručni projekt Izbor državne kartografske projekcije 1994., 1995., 1997. i 1998. godine.
Državna geodetska uprava Republike Hrvatske krajem 1999. godine prepoznala je problem matematičke osnove službene kartografije i naručila od Geodetskog fakulteta Sveučilišta u Zagrebu izradu projekta "Prijedlog službenih kartografskih projekcija Republike Hrvatske". Na temelju provedenih ispitivanja, uzevši u obzir analizu postojećih kartografskih projekcija u Republici Hrvatskoj, uvažavajući preporuke i iskustva međunarodnih tijela i udruženja, uzevši maksimalno u obzir nacionalne interese i potrebe za definiranje geodetskog prostornog sustava Republike Hrvatske predložene su sljedeće službene kartografske projekcije:
Tablica 1. Prijedlog službenih kartografskih projekcija Republike Hrvatske
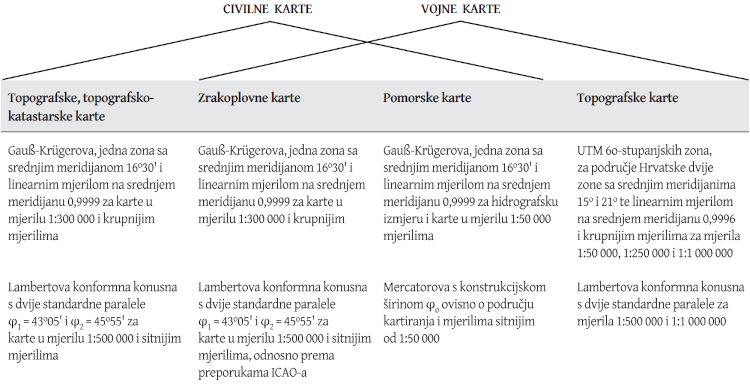
Na temelju Zakona o državnoj izmjeri i katastru nekretnina (Narodne novine, br. 128/99) Vlada Republike Hrvatske na sjednici održanoj 4. kolovoza 2004., donijela je Odluku o utvrđivanju službenih geodetskih datuma i kartografskih projekcija Republike Hrvatske. Prema toj Odluci:
Koordinatni sustav poprečne Mercatorove (Gauss-Krügerove) projekcije – skraćeno HTRS96/TM, sa srednjim meridijanom 16°30' i linearnim mjerilom na srednjem meridijanu 0,9999 određuje se projekcijskim koordinatnim sustavom Republike Hrvatske za područje katastra i detaljne državne topografske kartografije.
Koordinatni sustav uspravne Lambertove konformne konusne projekcije – skraćeno HTRS96/LCC, sa standardnim paralelama 43°05' i 45°55' određuje se projekcijskim koordinatnim sustavom Republike Hrvatske za područje pregledne državne kartografije.
Koordinatni sustavi kartografskih projekcija temelje se na hrvatskom terestričkom referentnom sustavu.
Za potrebe Oružanih snaga Republike Hrvatske usvaja se projekcijski koordinatni sustav univerzalne poprečne Mercatorove projekcije (Universal Transverse Mercator – UTM) sukladno Sporazumu o standardizaciji STANAG 2211, država članica NATO saveza, 5. izdanje od 15. srpnja 1991.
5. Kartografske projekcije u hrvatskom školstvu
O kartografskim projekcijama u Hrvatskim srednjim školama općenito se ne predaje gotovo ništa, a relativno malo u srednjim školama za obrazovanje geodetskog tehničara. To su: Geodetska tehnička škola u Zagrebu, Graditeljsko-geodetska škola u Osijeku, Građevinska tehnička škola u Rijeci, Tehnička škola u Puli, Graditeljsko-geodetska tehnička škola u Splitu, Srednja škola A. M. Reljkovića u Slavonskom Brodu, Obrtnička i tehnička škola u Dubrovniku i Graditeljska škola u Čakovcu.
Zavod za kartografiju Geodetskog fakulteta Sveučilišta u Zagrebu osnovan je aktom Sveučilišta u Zagrebu 22. svibnja 1956. na Geodetskom odjelu tadašnjega Tehničkog fakulteta. Osnivanju Zavoda za kartografiju prethodilo je osnivanje Katedre za kartografiju 1951. nakon izbora Branka Borčića za izvanrednog profesora, odnosno postupno formiranje Kartografskog laboratorija, što ga je započeo Ivan Kreiziger već 1948. Znatna nastavna djelatnost na području kartografije postojala je i prije osnutka Katedre za kartografiju. Međutim, od njezina se osnutka, a pogotovo od osnutka Zavoda za kartografiju, razvila i značajna znanstvena i stručna djelatnost.
Na današnjem Geodetskom fakultetu Sveučilišta u Zagrebu postoji dugogodišnji kontinuitet u nastavi kartografskih projekcija i geodetskog crtanja. O kartografskim projekcijama predavali su profesori: dr. Marije Kiseljak, dr. Vladimir Vranić, dr. Anton Fasching, Nikolaj Abakumov, dr. Franjo Braum, Mato Janković, dr. Branko Borčić, dr. Nedjeljko Frančula i dr. Miljenko Lapaine.
Stjepan Horvat (1895−1985) predavao je 30-ih godina 20. stoljeća Geodetsku kartografiju u okviru kolegija Državna izmjera, odnosno Premjeravanje države. O njemu se do nedavno vrlo malo znalo jer je nakon Drugog svjetskog rata bio prisiljen emigrirati. Za povijest kartografskih projekcija njegovi su radovi vrlo važni i po sadržaju i po opsegu. Ako bi se prebrojili samo njegovi radovi s područja geodezije i kartografije, dobio bi se broj veći od stotine, s ukupno više od 2000 stranica.
Antal (Antun, Anton) Fasching (1879−1931) bio je jedan od najizobraženijih mađarskih geodeta. Napisao je oko 70 radova. U Zagrebu je predavao Višu geodeziju, Kartografiju, Državnu izmjeru i Fotogrametriju u razdoblju od 1923. do 1928. godine. Osim nastavnog rada, za teoriju kartografskih projekcija vrlo je važan i njegov znanstveni rad, u prvom redu na rješavanju pitanja izbora državne projekcije.
Nikolaj Pavlovič Abakumov (1882−1965) izabran je 1927. za redovitog profesora na Geodetskom odjelu Tehničkog fakulteta u Zagrebu i tu je do potkraj 1950. predavao Državnu izmjeru, Višu geodeziju, Sfernu astronomiju, Praktičnu astronomiju, Primijenjenu astronomiju, Pozicionu astronomiju, Fotogrametriju, Kartografiju, Matematičku kartografiju, Primijenjenu kartografiju i Geofiziku. Spomenimo da je Borčić, pišući svoj udžbenik Matematička kartografija, citirao u popisu literature i predavanja profesora Abakumova na Tehničkom fakultetu u Zagrebu.
Branko Borčić (1908−1977) doktorirao je 1964. na Fakulteti za arhitekturo, gradbeništvo in geodezijo u Ljubljani tezomMatematička podloga karte svijeta u mjerilu 1 : 1 000 000. Od 1951. izvanredni je profesor na Tehničkom fakultetu u Zagrebu, gdje se 1956. habilitirao radom Prilog rješavanju transformacije koordinata između susjednih koordinatnih sistema kod Gauss-Krügerove projekcije. Od 1960. redoviti je profesor Arhitektonsko-građevinsko-geodetskog fakulteta u Zagrebu. Pisao je o pitanjima matematičke i geodetske kartografije te objavljivao u Geodetskom glasniku (1939−40), Geodetskoj službi (1951), Geodetskom listu (1955, 1960, 1975), Građevinaru (1958). Njegovi su se udžbenici o kartografskim projekcijama i Gauss-Krügerovoj projekciji koristili godinama kao jedini priručnici te vrste u Hrvatskoj (slika 11).
Nedjeljko Frančula diplomirao je 1962. na Geodetskom odjelu Arhitektonsko-građevinsko-geodetskog fakulteta u Zagrebu. Doktorirao je 1971. u Bonnu (Landwirtschaftliche Fakultät) tezomDie vorteilhaftesten Abbildungen in der Atlaskartographie. U svojoj doktorskoj disertaciji Frančula je istraživao projekcije koje bi bile najbolje za izradu karata svijeta. Pri tome je predložio 14 novih projekcija koje su prema njemu dobile ime Frančula I−XIV (Jung 2021,slika 12). U trajno zvanje redovitog profesora za područje tehničkih znanosti − polje geodezija izabran je na Geodetskom fakultetu Sveučilišta u Zagrebu 1996. godine. Osim u Zagrebu predavao je na dodiplomskom i poslijediplomskom studiju i na Fakultetu za arhitekturu, građevinarstvo i geodeziju u Ljubljani 1974–76. Senat Sveučilišta u Zagrebu imenovao ga je professorom emeritusom 2007, a 2008. proglašen je za člana emeritusa Akademije tehničkih znanosti Hrvatske. Hrvatsko geodetsko društvo dodijelilo mu je 2013. nagradu za životno djelo Zlatni globus.
Miljenko Lapaine diplomirao je na Prirodoslovno-matematičkom fakultetu Sveučilišta u Zagrebu na području teorijske matematike. Doktor tehničkih znanosti na Geodetskom fakultetu Sveučiliša u Zagrebu postao je obranom disertacijePreslikavanja u teoriji kartografskih projekcija. Professor emeritus je od 2018. godine. Objavio je više od 1000 radova. Sudjelovao je kao predstavnik Hrvatske na svim međunarodnim kartografskim konferencijama u organizaciji Međunarodnoga kartografskog društva (International Cartographic Association − ICA) od 1989. do 2019. godine. Njegovom zaslugom Hrvatska je 1995. godine postala punopravnom članicom ICA-e. Miljenko Lapaine izabran je za počasnog člana ICA-e (Honorary Fellow of the ICA) u znak priznanja za njegove mnogobrojne izvanredne doprinose ICA-i i za njegovu iznimnu promociju kartografije na međunarodnoj razini. Predsjednik je Hrvatskoga kartografskog društva i izvršni urednik časopisa Kartografija i geoinformacije.
6. Zaključak
Kartografske projekcije posebna su grana kartografije. Mogu se podijeliti na razne načine. Osnovni problem teorije kartografskih projekcija je u tome što se sferna ili elipsoidna ploha ne mogu preslikati u ravninu bez deformacija. Povijesni razvoj kartografskih projekcija započinje nekoliko stotina godina pr. Kr., a traje do danas. Kartografske projekcije imale su i imaju svoju primjenu u Hrvatskoj. U članku su istražene i prikazane službene kartografske projekcije u Hrvatskoj i kartografske projekcije u hrvatskom školstvu.


















