INTRODUCTION
Authenticating with signatures individually can be considered as major attributes of a person. Like other authentication methods such as smart cards, fingerprints, PINs and passwords, signatures cannot be forgotten, lost or stolen. That is why the there is a huge demand for signature verification. The major challenge is to come up with more accurate automated signature verification systems. This handwritten signature verification can be done online and offline automatically. In online signature verification system many electronic devices like digital pens, digitizers and tablets are used. You need a still image to see your signature offline. Verification of the signatures in offline is the method used most commonly as it requires no additional equipment to record the signature which can be done even without a signer. If a person tries to copy the other person’s signature without his knowledge, it is considered as a forgery. This forgery can be divided as three different categories: random, trick and simple, depending on the knowledge of the signature done by a forger. Forger creates its own dash pattern because it has information about the signer's name when it doesn't know the exact signature. It is an example for a simple forgery. Suppose counterfeiter attempts to counterfeit without knowing the name or signature, this is a random counterfeit. Over the last two decades, the field of signature verification has created many innovations on behalf of many other researchers. In the local histogram feature approach1-7, polar and Cartesian coordinates are used to separate the signature into different zones. In each zone, Histogram features like Directional Gradient (HOG) Histogram and Local Binary Pattern (LBP) Histogram has to be calculated. In LBP, there is variant called Block wise Binary Pattern (BBP)8 which is generally used to separate a signature into many 3×3 blocks. Another method, known as writer independent9 values properties such as shape and texture of a signature. This method extracts black and candidate pixels. The distance moment10 based on the structural information and point-to-point temporal records of envelope by finding out the point-to-point distance. A novel autonomous system for signature detection depending on architecture of neural network has been proposed by Shikha et al.11. Self Organizing Map (SOM) is the learning algorithm used, which classifies patterns based on a Multilayer Perceptron (MLP). Shekaret et al.12 proposed a morphologically structured spectrum constructed in the form of a lattice. The signature is equally divided into 8 grids of same size using this method. A different method was proposed by Bhattacharya et al.13 called as Pixel Matching Technology (PMT). The reference signature is mapped with each pixel in the template of a signature in this approach. SVM based verification is done in a system which verifies the offline signature proposed by Sheth and Kruty14. Yasmine et. al15 proposed a new one class SVM based system which verifies the signature online. The template of an original signature done by a signer is used in this method.
RELATED WORKS AND MOTIVATION
Signatures are the most socially and legally recognized means of personal authentication and, therefore, a modality that faces high levels of attack. Signature verification plays an important role in identifying forged signatures. Biometric application. Biometrics measures an individual's unique physical or behavioral characteristics with the goal of recognizing or authenticating an identity. This motivates to develop an high accurancy based offline signature recognition system. The performance of a validation model depends on the set of features used in the model. Much work has been done in connection with offline signature verification, which uses different types of feature sets to work with the model. In most works, the features are topology, geometric information, gradients, structural information, and concave base16,17. Ferrer et al.18 proposed a method using the set of geometric features given in the description of the signature envelope and stroke distribution. After that, hidden Markov models, support vector machines and Euclido removal classifiers were used for review processes. Zulnarnain et al. In recent works, a signature inspection method was introduced based on geometric features such as triangular pages, angles and ranges derived after triangulation of the signature image. For classification, they used Euclidean classifier and voting based classifiers. Some plants are reported for gray value distribution20,21, pixel orientation22-24, pixel environment25 and curvature functions26. Graph metric functions are also available in the literature27. In28, the authors proposed a form function called a string torque and analyzed the upper and lower signatures. Support vector machine (SVM) was used with code characteristics for signature confirmation. One model has been used in combination with several features to improve the classification accuracy of the model. For example, in29 with directional characteristics, exercise information and gray value distribution were used. The authors used 16 serious features obtained from the distribution of pixels in the diluted Signature valley. Combinations of different types of characteristics express feature extraction unit. Of course, to use a model for 16 time applications, momentary information calculations are mathematically considered with 16 timing functions. In the recent work30 proposed by Serdouk et al., Directional distribution is not the only feature extraction policy. Here, combining the longest barrel function in the direction combined with the gradient of the local binary pattern (GLBP), and the longest run strengthens the horizontal, vertical direction, and two main diagonal directions considered Combined to do. So you used a combination of topology and color history features. As a phase feature, the longest pixel is used. Gradation information is extracted with neighboring local binary patterns (GLBP). GLBP calculations on each pixel of the signature image can cost cost. Serdouk et al. We proposed a verification system based on the artificial immune recognition system. A template-based validation scheme is also presented31. The method they provide is based on using a grid template to encode the geometry of the signature. Also note that many prior art works use an ensemble of multiple classifiers to achieve the best results. Oi et al.32 Recent studies have presented a framework based on discrete Radon transforms (DRTs), principal component analysis (PCA), and stochastic neural networks (PNNs) to identify counterfeiting from actual signatures. rice field. However, in an application, the designed hardware device needs to run fast for classification and decision making. Table 1 outlines the existing methods and their classification methods. Zois Elias et al.33 addresses a feature extraction scheme based on the detection of first-order transitions between asymmetric lattice arrangements of simple pixel structures. Experiments were conducted with a group of decisions, accompanied by a selection of reinforcement features, using only unlinked or blinded training and test datasets, all derived from four widely used signature database. Sharif et al.34 used the geometric features and the features generated from the study of the local pixel distribution. They used genetic algorithm-based feature selection and eventually SVM for the classification work. Batool et al.35 presented a way to generate features by determining the pixel distribution in the signature area. I used SVM for classification. The ratio of training and test variables is shown in the experiment as 70:30. Ajij et al.36 introduces a new feature set based on the quasi-straightness of boundary pixel execution for signature verification. The basic combination of direction codes extracts the quasi-segments from the signature boundary pixels and retrieves the feature sets from the various quasi-line classes. Several methods or detection models have been developed, but the results of existing methods confirm that there is still room for improvement in terms of accuracy and robustness. In addition, you have the opportunity to propose a powerful feature set that works in conjunction with less complex classifiers for better performance. It would be even more beneficial if the feature set could be easily extracted from the signature image. In this article, we have proposed a new feature set from the Extreme Points Warping that defines the signature stroke. The following sections detail the proposed methods and test results. The contributions of this article are described further in the text. • This method introduces a new way to select features from signatures. This combination of forms a new signing feature. • In our approach, the average of the extracted features passes through a classifier for verification. • However, by demonstrating the experiment based on the actual data set, the robustness and efficiency of the proposed method.
PROPOSED TECHNIQUE
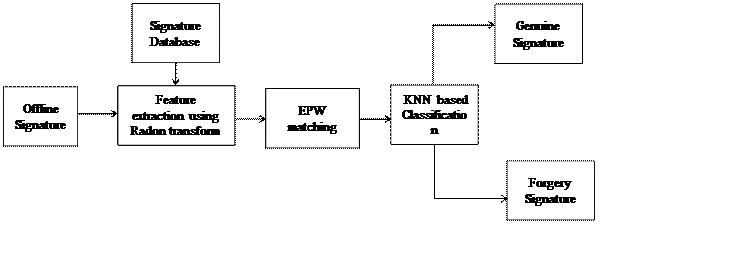
The block diagram of proposed forgery signature recognition system is shown in Figure 1. System consists of different blocks which will explain below. The system that we have introduced is divided into three phases: (a) Enrolment of signatures (Creating model) (ii) Training the signatures (iii) Signature Verification. The given system’s block diagram is described in Figure 1.
In the first phase, to find the parameters which characterize the variance of the signatures which are used as a reference, we use a set of signatures for reference. The extracted parameters along with the set of reference signatures are stored in the system database with unique user identification. During training phase we select few signatures which are genuine and forged to train K-NN classifier. Further in third phase, the claimed person’s signatures which are used for references are compared with the test signature. If the similarity measure is greater than or equal to the threshold value given in classifier, then the authentication of person is done and it will be denied otherwise.DRT & EXTRACTING THE FEATURE
Discrete Radon Transform is a representation of a shadow or a projection at an angle of original image in each column of a matrix. It is expressed as follows:
R_j=∑_(i=1)W_ij I_i,...j = 1, 2, ..., Nφ·Nθ. (1)
where Rj is jth beam pixels overall intensity, Ψ denotes overall image pixels, wij is the donation of ith pixel to jth beam sum. Furthermore, Ii is ith Pixel’s intensity, Nφ is Beams/angle which are non-overlapping and Nθ is total number of angles. The pen-strokes and background of a signature image has to be mapped to one and zero respectively to extract the global features. Then the speckle noise is removed using median filtering. Finally the signature image’s DRT is found.
ALIGNMENT OF SIGNATURE
To compare the signatures of different lengths Extreme Points Warping Algorithm is used. Rather than warping the whole signal, only few selected (Peaks & Valleys) important points will be warped in Extreme Points Warping (EPW) algorithm. The minimum total distance between the two vectors will be found to get the best straight alignment between the two vectors. We need to align the observation sequence to make sure that every observation sequence is a signature image’s rotation invariant representation. Two observation sequences optimal alignment is obtained in linear way. Then the observation sequences are shifted iteratively with respect to one another. Calculation of the distances between corresponding observations is done in any iteration. When the average distance is minimum between the consecutive observations, then the alignment will be optimal. The average distance between the optimally aligned vectors can be found to get the distance between two signatures.
ENROLLMENT
Five signatures are used for each user in our system during enrolment to this system. The distance between each of the pair is found by pair-wise aligning these signatures, with the help of EPW algorithm. We calculated the following reference set statistics using the alignment scores obtained: a. Average distance to the farthest signature, (dmax) b. Average distance to the nearest signature, (dmin)
TRAINING
In training data set we have two: five- signatures, where one of them is genuine signatures and remaining is forgery. These signatures will be used to get the threshold value which helps us to separate the genuine and forgery classes. The reference signatures are different from these signatures. Initially we need to compare each training signature with signatures in the reference set which is claimed to belong. We use EPW algorithm for that which gives a 2-D feature vector (pmin, pmax). These values are normalized by taking the averages of the corresponding reference set (dmin, dmax) the feature set distribution is found by using equation (2) and (3).
Nmax = dmax/pmax, (2)
Nmin = dmin/pmin. (3)
With the normalized features, forgery and genuine samples in the training set are separated well due to the distribution of these normalized data. We can see that the distance measured of the vectors is normalized by the averages of corresponding reference set. By this we can remove the user dependent thresholds need which is generally used while deciding whether the given signature is similar enough to that of the reference set.
CLASSIFICATION
The Trained classifier is tested using the data set which consists of five genuine and five forgery signatures. The signatures used during the enrolment and training phases are different from these signatures. To find whether the test signature is forgery or genuine, first we need to compare the signature with all the reference signatures which belongs to the ID claimed using EPW algorithm. The distance values (pmin, pmax) which are normalized by the averages of reference set who claimed it (dmin, dmax), Finally trained classifier is used to classify whether the signature is forgery or genuine by using the normalized values.
EXPERIMENTAL RESULTS
Proposed system uses 30 genuine signature patterns and 20 Skill forged signature patterns for each user. In addition, we've added five real-world signature samples from a random user to avoid getting fake signatures from the skill. Similarly, in the testing phase, another 10 original signature samples from the same user, 5 skill counterfeit signature samples from that user, and 5 original signature samples from user are combined and tested. The signature verification efficiency is evaluated by two parameters: (i) false acceptance rate (FAR) and (ii) false rejection rate (FRR). Recognition rate is one more parameter to consider when assessing classifier performance. Details and examples are given in Figures 2-7.
Type I error or False Rejection Rate (F R R) FRR=(No.of genuine signatures identified as forged)/(No.of genuine signature samples) ×100 %. (4)
Type II error or False Acceptance Rate (F A R): FAR=(No.of forged signatures identified as genuine)/(No.of forged signature samples) ×100 %. (5)
Recognition rate: The classifier accuracy is identified by this parameter, which is given by: Recognition rate=(No.of correctly indentified signature samples)/(No.of signature samples) ×100 %. (6)
| Users | No. of signature | FRR | FAR | Accuracy |
| User1 | 50 | 5/50 = 10 % | 3/50 = 6 % | 45/50 = 90 % |
| User 2 | 50 | 3/50 = 6 % | 4/50 = 8 % | 47/50 = 94 % |
| User 3 | 50 | 4/50 = 8 % | 2/50 = 4 % | 46/50 = 92 % |
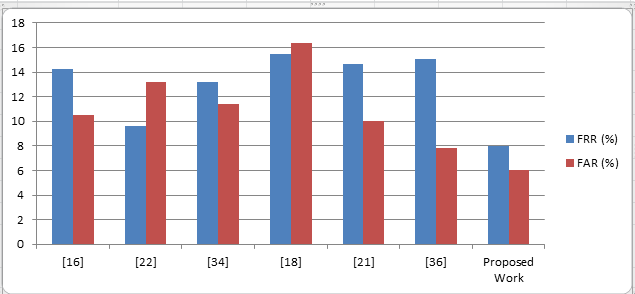
| Methods | FRR ( %) | FAR ( %) |
| 16 | 14,21 | 10,48 |
| 22 | 09,64 | 13,16 |
| 34 | 13,16 | 11,38 |
| 18 | 15,50 | 16,39 |
| 21 | 14,66 | 10,01 |
| 36 | 15,04 | 7,85 |
| Proposed Work | 8 | 6 |
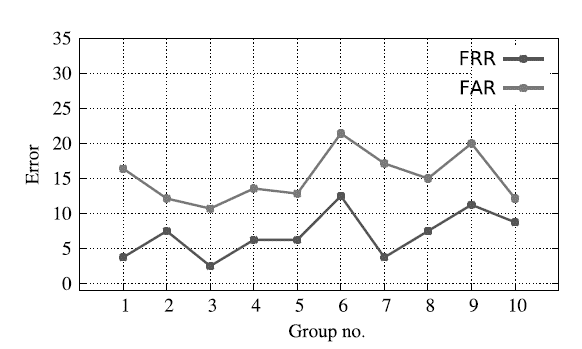
Good results obtained for many individuals (50 signers), but poor results for some one reduces the overall average accuracy. We have showed the error rate for each group of our data set in Figure 6. In which each group has 50 signers. In this study, we measured the performance of the proposed system with characteristics of each signature after the KNN was implemented in the signature to represent it in the validation system as shown in Table 2. In addition, the study estimated 93,1 % recognition accuracy using 100 users with 5 000 signature samples. It is also clear that a small number of signature features during the training phase will result in less valid results, higher FARs and FRRs, and less accuracy. It is also noted that the work has achieved a comparable and sometimes better performance than other systems as shown in table 3. From Figure 8 it is clearly indicated that proposed method having less error rate (FAR, FRR) compare to various existing methods.
In addition, the results obtained in this experiment show that not only the components (as a function) obtained from the KNN analysis widely adopted in previous studies, but also other items can be used for online and offline signature verification.CONCLUSIONS
In this offline signature classification, two class pattern recognition is used to approach the problem which uses the K-NN classifier. The robust and stable method, DRT is used to extract the global features of the signature. DRT establishes simulated evolution of time evolution from one vector feature with the next and using EPW it helps us to develop a signature model. The validation results confirm the better effectiveness of the proposed method, as it achieved an accuracy of 93,1 % with 100 users and 5 000 signatures consists of real and artificial signatures.