1. INTRODUCTION
Vibratory conveying devices (vibratory conveyors, bowl feeders, vibratory elevators) are widely employed in various industries. The most common and constructively simple conveying devices are equipped with a drive, performing harmonic (sinusoidal) oscillations, the conveying track with a linear trajectory of vibration at a certain angle to the plane of conveying[1-3]. Generally, they transport relatively small and not very massive products by moving them with hopping. However, for conveying heavy and bulky cargo or fragile and explosive products, it is necessary to ensure the moving of products without hopping. But to achieve a high conveying velocity, it is necessary to ensure a large amplitude of longitudinal oscillations, and in vibratory devices with linear harmonic oscillations, the increase of vibration amplitude inevitably leads to the moving of products with hopping. The increase of conveying velocity in non-hopping modes, and as a result, the enhance in productivity, can be reached in vibratory devices with independent longitudinal and normal (two-component) vibrations of the conveying track. The simplest example of two-component vibration is elliptical vibration when longitudinal and normal oscillations are harmonic with a phase difference between them, and the conveying track vibrates in an elliptical trajectory[2,4,5]. Theoretical and experimental studies show that vibratory conveying by elliptical vibration significantly enhances the conveying velocity and expands the elevation angles compared to conveying by linear harmonic vibration. Even higher values of velocity and elevation angles can be reached by implementing polyharmonic oscillations. Vibratory conveying by polyharmonic oscillations is considered in[6-8].
The maximal conveying velocity is achieved when both components (longitudinal and normal) are oscillations with piecewise constant acceleration[9,10]. However, the large amplitude of longitudinal oscillations, necessary to ensure high velocity, can be achieved using inertial or electromagnetic drives, which implement harmonic vibration in industrial conveying devices, usually in near-resonant modes, when non-sinusoidal vibration is difficult to obtain. At the same time, the amplitudes of normal oscillations should be relatively small in non-hopping modes of the products’ moving, when the maximal normal acceleration does not exceed the gravitational acceleration g. In this way, it is much easier to implement non-sinusoidal normal oscillations. Therefore, the author proposed to use longitudinal harmonic oscillations and normal oscillations with piecewise constant acceleration, the conveying with which was studied in[11] by an approximate harmonic balance method and in[12] only for a mode without stages of particle’s standing relative to vibrating track. However, when using these results, the accuracy of determining velocity is insufficient, especially at large inclination angles and the large asymmetry of normal oscillations. The optimal values of the phase difference angle have not been determined, but they significantly affect the conveying velocity.
The purpose of this paper is to investigate vibratory conveying by longitudinal harmonic oscillations and normal oscillations with piecewise constant acceleration, using a step-by-step integration method, which makes it possible to study the conveying velocity dependence on vibration parameters and to determine their optimal values, in particular, the value of phase difference angles, with a given accuracy.
2. EQUATIONS OF THE MOTION OF A MATERIAL POINT ON THE VIBRATING TRACK
Theoretical and experimental investigations have shown that the theory of a material point moving on a vibrating surface with dry friction describes with sufficient accuracy the process of vibratory conveying of piece products [2,13-16]. This paper continues the previous author’s study [7,12], where the vibratory conveying with longitudinal harmonic and polyharmonic normal oscillations was considered. It describes the vibration of the conveying device’s track, inclined to the horizon under angle α, by equations in the fixed Cartesian coordinate system X1OY1 (Figure 1); the X-axis is taken along the inclined upward direction (longitudinal) on a track’s plane, and the Y-axis is taken perpendicularly (normal) to a plane:
(1)
where A is the amplitude of longitudinal oscillations, Ai is the amplitude of ith harmonic of normal oscillations, ω is the frequency of oscillations, n is the number of harmonics, ε is the phase difference angle, and t is the time.

Fig. 1 Diagram of the forces acting on a conveying particle
The effectiveness of the process of vibratory conveying can be estimated by the value of dimensionless velocity V, which determines the mean conveying velocity v per unit frequency and amplitude of longitudinal oscillations:
(2)
Having determined the value of V, we can calculate the vibratory conveying velocity at the known amplitude and frequency of longitudinal oscillation: v = AωV.
Differential equations describe the motion of a particle of mass m in the coordinate system XOY (Figure 1) connected with a vibratory track[13]:
(3)
where F is the frictional force, N is the force of normal reaction, and frictional force changes according to the dry friction law: –μN ≤ F ≤ μN, where μ is the frictional coefficient. Using the values of dimensionless time τ = ωt and dimensionless distance χ = x / A, the system of Eqs. (3) in the motion modes without hopping (y = 0), can be represented by different equations, describing acceleration χ″ and velocity χ′ as the functions of dimensionless parameters, in different stages of movement during the period of oscillations T. Using step-by-step integration method, dimensionless velocity V dependence on several dimensionless parameters was investigated with the optimal condition, when the minimal normal acceleration is equal to the gravitational acceleration g. Velocity V achieves its maximum at the certain (optimal) values of difference phase angles ε and the certain ratios of normal harmonics’ amplitudes. In turn, these optimal values depend on a number of harmonics n, on the inclination angle parameter Θ, and the vibration parameter q, which are determined as follows:
(4)
In particular, it is shown that dimensionless velocity V increases with the increase in the number of harmonics n, but with each successive number n, this increase is less significant. Thus, the use of polyharmonic normal oscillations with n > 10 is irrational, and it is more profitable to use normal oscillations with piecewise constant acceleration.
3. VIBRATORY CONVEYING WITH DIMENSIONLESS PARAMETERS PROVIDING MAXIMUM VELOCITY
Two-component vibration that includes the longitudinal harmonic oscillations and the normal oscillations with piecewise constant acceleration (piecewise linear velocity) was studied in[12], presenting the variation of acceleration in the form (Figure 2a), described as follows:
(5)
where , , .
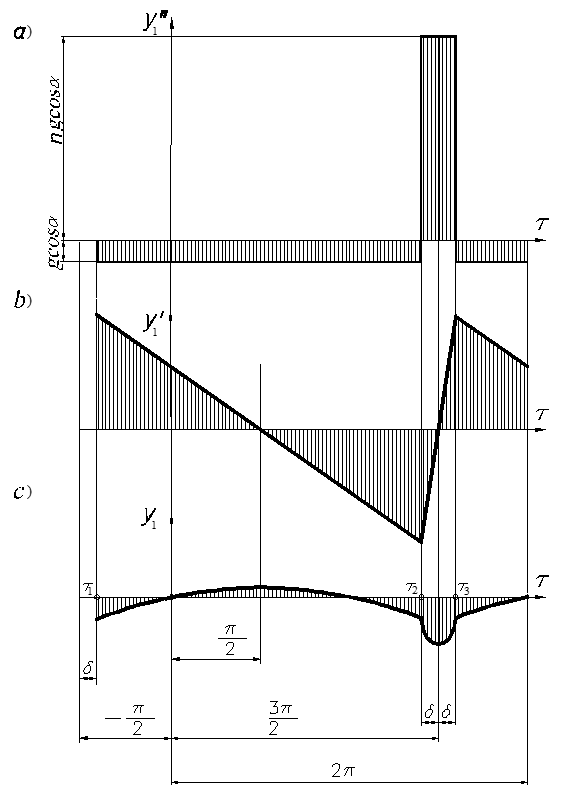
Fig. 2 Normal oscillations with piecewise constant acceleration:
a) acceleration; b) velocity; c) displacement
By integrating Eq. (5) twice, we obtain the equations for the variation of vibration velocity (Figure 2b) and displacement (Figure 2c) in the normal direction: piecewise linear velocity and displacement in the form of two segments of parabolas during the period of vibration.
(6)
where . The values of the integration constants are determined from the condition of continuity of the function y(τ).
Thus, we represent two-component vibration with longitudinal harmonic oscillations x1 and normal oscillations y1 with piecewise constant acceleration, described by equations:
(7)
After substitution these equations in the system of Eqs. (3), using the values of dimensionless time τ = ωt and dimensionless distance χ = x / A, in the non-hopping modes of motion (when y=0), under the methodology described in [7], we obtain the equation of the varying of moving particles acceleration during the period of vibration:
(8)
The values of θ1,2± in Eq. (8) are different for different stages of the particle’s moving. The graph of dimensionless velocity χ′ varying during the vibration period on different stages is shown in Figure 3.
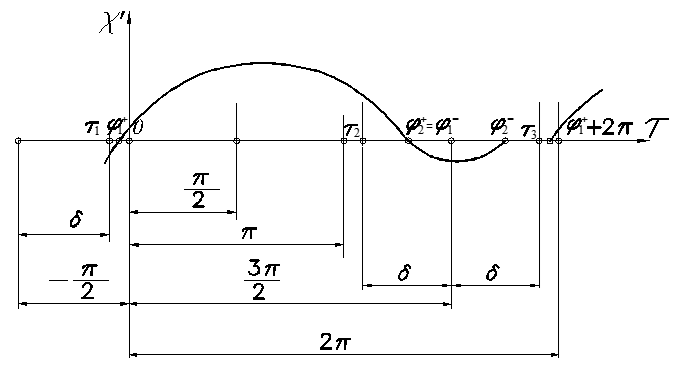
Fig. 3 Conveying velocity variation during vibration period in the motion mode with stick (+ – 0)
The particles move in different modes, depending on the existence of different stages during the period of vibration, these stages can be sliding motion forward, sliding motion backward, and standing without moving, relative to the vibrating track (stick)[13]. Let us indicate sliding motion forward by “+”, sliding motion backward by “–” and stick (standing relative to vibrating track) indicated by “0”. To reach the maximum velocity V, it is necessary that the stage of sliding motion backward (–) is situated inside the region τ2 < τ < τ3, and the stage of sliding motion forward (+) begins at . The stage of sliding motion forward lasts from τ = φ1+ to τ = φ2+, and sliding motion backward lasts from τ = φ1– to τ = φ2–. The stage of sliding motion forward consists of two steps: 1st step, which lasts from τ = φ1+ to τ = τ2, in which the frictional force F = 0 and in Eq. (8) θ1,2± = θ1 = qΘ, and 2nd step, that lasts from τ = τ2 to τ = φ2+, in which the frictional force and θ1,2± = θ2+ = q (1+n+Θ). The stage of sliding motion backward (step 3) lasts from τ=φ2+=φ1– to τ=φ2–, in which and θ1,2± = θ2– = –q (1+n–Θ). The last step 4 - the stage of standing without moving (stick) lasts from τ = φ2– to τ = φ1+ + 2π. This mode (+ – 0) is the mode 3A according to the classification by Blekhman[13].
The value of φ2+ is determined as the nearest root (φ2+ > φ1+) of equation:
(9)
Equating φ1– = φ2+ then determine φ2– as the nearest (φ2– > φ1–) root of equation:
(10)
Integrating Eq. (8), we obtain the dependencies of variation in a particle’s velocity at all steps:
(11)
(12)
(13)
Dimensionless velocity can be determined by the formula[12]:
(14)
where S1, S2, S3, and S4 are the dimensionless distances of a particle at four different steps during the vibration period (Figure 3), calculated by equations:
(15)
(16)
(17)
On the 4th stage of stick S4 = 0.
The maximum velocity is achieved when φ1+ =τ1, the condition of it, as follows from Eq. (8), is= τ1. Thus, the optimal value of the phase difference angle for this mode (+ – 0) is determined by the formula, obtained from the system of Eqs. (9), (10):
(18)
In certain circumstances (a large value of n, when q (1+n–Θ) ≥ 1, or when there are no solutions of the system of Eqs. (9), (10) on the segment τ2 < τ < τ3), the stage of sliding motion backward is absent. In this case, the mode (+ 0) – mode 4A in classification by Blekhman[13] is released, and S3 = S4 = 0 in Eq. (14). When the solution of the system of Eqs. (8), (10) φ2– ≥ φ1++2π, the mode without sticks (+ –) – mode 2[13] is released, which was considered by the author in[12]. The conveying velocity χ′ variation during the vibration period on different steps of this mode is shown in Figure 4[12].
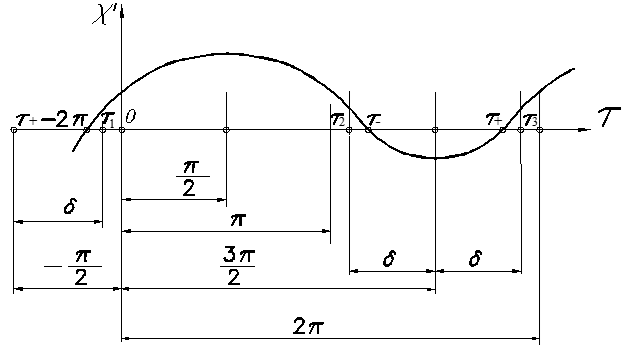
Fig. 4 Conveying velocity variation during vibration period in the motion mode without sticks (+ –)
The stage of sliding motion forward consists of three steps: the 1st step lasts from τ = φ1+ = τ+ – 2π to τ = τ1, in which θ1,2± = θ2+ = q (1+n+Θ) in Eq. (8), the 2nd step lasts from τ = τ1 to τ = τ2, in which θ1,2± = θ1 = qΘ and the 3rd step lasts from τ = τ2 to τ = φ2+ = τ–, in which θ1,2± = θ2+ = q (1+n+Θ). The stage of sliding motion backward lasts from τ = τ– to τ = τ+, in which θ1,2± = θ2–= –q (1+n–Θ). Integrating Eq. (8), we obtain the dependencies of variation in a particle’s velocity at four steps of stages:
(19)
(20)
(21)
(22)
The initial moments of the sliding motion forward τ = τ+ and sliding motion backward τ = τ– are determined as the roots of the system of nonlinear equations:
(23)
(24)
The dimensionless distances of a particle at four different stages during the vibration period (Figure 4) are calculated by equations:
(25)
(26)
(27)
(28)
Equations (19)-(28) were obtained by the author in[12].
The boundary between modes (+ – 0) and (+ –) (modes 3A and 2, according to[13]) depends on the relationship between parameters n, q, and Θ, and can be determined from Eqs. (9), (10) with unknown τ– and one of these three parameters, assuming φ2– = τ3:
(29)
(30)
Figure 5a demonstrates the relationship between these parameters on the boundary between modes as the dependence of limited value q1 on Θ and n. The mode 2 (+ –) takes place at q < q1; the modes 3A and 4A (+ – 0) or (+ 0) – at q > q1. Usually, in the vibratory conveying devices used in industry, particularly devices with electromagnetic drives, the value of the parameter is within 0.01 < q < 0.1. As is seen from Figure 5a, the vibratory devices with not very large asymmetry of normal oscillations (n < 4) will work in mode 2 (+ –).
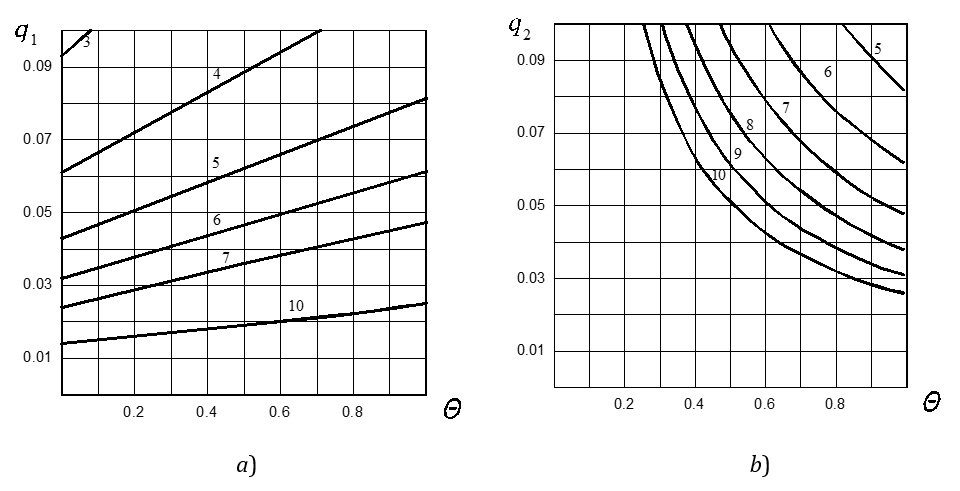
Fig. 5 Dependence of limited values of parameter a) q1 and b) q2 on inclination angle parameter Θ with different indexes of asymmetry n from 1 to 10
As the studies show, in this mode, the maximum V occurs when the final moment of the sliding motion backward τ+ = τ3. Using this in the system of Eqs. (23), (24), we obtain a formula for determining the value of optimal phase difference angle in mode (+ –):
(31)
Equations (18) and (31) give the same value of optimal angle εo at q = q1.
With a certain relationship between parameters (the large values of Θ and n), the final moment of the sliding motion forward φ2+ < τ2, and it needs to decrease the angle ε, calculated by Eq. (18), in order to ensure φ2+ = τ2. The boundary of this relationship can be determined from the system of equations with unknown ε and q:
(32)
(33)
This system of equations allows the optimal angle εo when q > q2 to be determined. However, when q < q2, the value of angle εo is determined from Eq. (18). The graphs of the boundary for determining the optimal angle ε are presented in Figure 5b as a dependence of limited value q2 on Θ and n.
4. DEPENDENCE OF VELOCITY ON DIMENSIONLESS VIBRATION PARAMETERS
By setting the values of dimensionless parameters Θ, q, n, the initial and final moments of steps of motion can be determined from the system of Eqs. (9), (10), or (23), (24). Then, it is possible to determine the particle moving mode (2, 3A, or 4A) and calculate the value of dimensionless velocity V from Eq. (14), substituting into it the values of dimensionless distances at different steps from Eqs. (15)-(17) for modes 3A and 4A or (25)-(28) for mode 2. For the calculations, a MathCAD-program was developed, which determines the motion mode, and then calculates the dimensionless velocity V and the optimal angles ε = εo from Eqs. (18), (31), or (32)-(33) with a step-by-step integration method, obtaining a result with a given accuracy.
The maximum value of V is reached at a certain phase difference angle ε = εo, which depends on parameters Θ, q, and n. The inclination angle parameter varies in the range 0 < Θ < 1 from horizontal conveying (α = 0) to the maximal inclination angle, equal to the angle of friction. Dimensionless velocity V is almost independent of the parameter q, which varies in the range 0.02 < q < 0.1. The dependencies of velocity V on inclination angle parameter Θ, with values of parameters 0.02 < q < 0.1, for the index of asymmetry n = 1 – 10 are shown in Figure 6 by continuous lines. For comparison the same dependencies for polyharmonic normal oscillations with a number of harmonics n, equal to the corresponding value of index asymmetry, are shown by dashed lines.
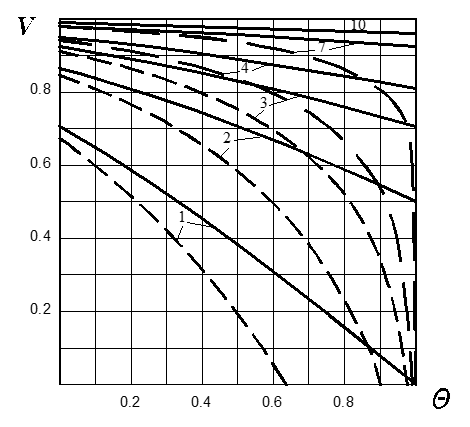
Fig. 6 Dependence of dimensionless velocity V on inclination angle parameter Θ with vibration parameter q = 0.05 and different indexes of asymmetry n from 1 to 10
Maximal dimensionless velocity V, decreases with the increasing of inclination angle parameter Θ. It is irrational to use the values of Θ > 0.9, because the stability of conveying may be disturbed due to the possible variability of the frictional coefficient.
The comparison between vibratory conveying by normal oscillations with piecewise acceleration and the one by normal polyharmonic oscillations shows the advantage of the former in velocity values, especially with the increase of inclination angle parameter Θ (increasing of lifting angles α).
The dependencies of dimensionless velocity V on the index of asymmetry n with different values of inclination angle parameter Θ are shown in Figure 7.
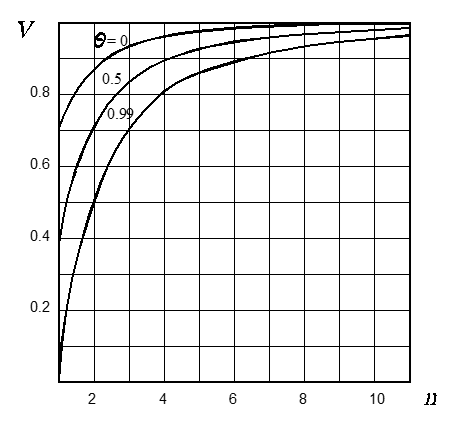
Fig. 7 Dependence of dimensionless velocity V on the index of asymmetry n with vibration parameter q=0.05 and different inclination angle parameters Θ
Velocity V increases as n increases, however, with each subsequent increase in n, the increase in V is less significant. The value of dimensionless velocity V increases more essentially at large values of parameter Θ. It is irrational to use the values n > 10, even at large values of Θ, because the increase of V becomes minimal, but the load on the device’s drive increases.
5. DEPENDENCE OF OPTIMAL PHASE DIFFERENCE ANGLE ON DIMENSIONLESS VIBRATION PARAMETERS
Maximum dimensionless velocity V is achieved at the optimal value of phase difference angle ε = εo, which varies within Θ < εo < 90° and depends on the values of parameters Θ, q, and n.
Graphs of optimal angle εo dependence on parameters Θ with different indices of asymmetry n are shown in Figure 8a for q = 0.01 and in Figure 8b for q = 0.1. Continuous lines in Figure 8a show graphs at n = 1, 3, and 10, dashed lines – graphs at n = 2 and 5; c>ontinuous lines in Figure 8b show graphs at n = 1, 5, and 10, dashed lines – at n = 3 and 7. Graphs of optimal angle εo dependence on the index of asymmetry n with different values of the parameter are shown in Figure 9a for q = 0.01 and in Figure 9b for q = 0.05. Continuous lines in Figure 9b show graphs at Θ = 0 and 0.9, dash-dot line – graph at Θ = 0.3, and dashed lines – at Θ= 0.5 and 0.7.
As is seen from Figures 8 and 9, the optimal phase difference angle εo increases with the increase in parameters n and Θ at small values of parameter q. The change of εo is less significant with increasing n, and at the certain value of Θ, which decreases with increasing q, optimal angle εo practically does not depend on n, and with a further increase in Θ, angle εo decreases with increasing n. In contrast to the dependence of dimensionless velocity V, which is almost unaffected by q, the optimal phase difference angle εo significantly depends on q. The optimal angle εo always increases with the decrease in parameters q.
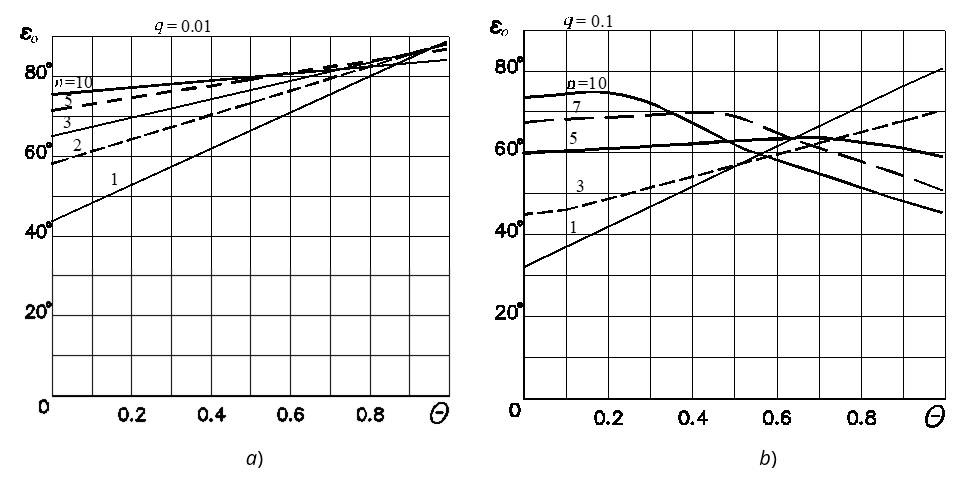
Fig. 8 Dependence of optimal phase difference angle εo on inclination angle parameter Θ with different indexes of asymmetry n: a) q = 0.01; b) q = 0.1
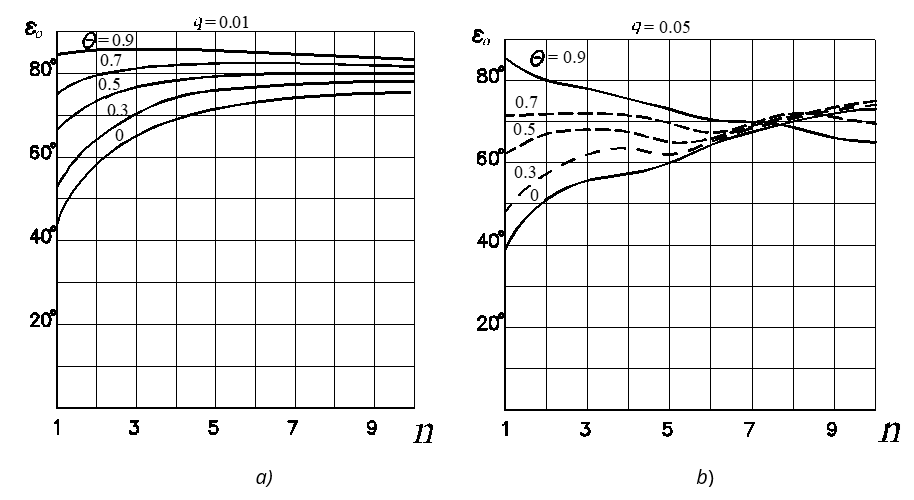
Fig. 9 Dependence of optimal phase difference angle εo on the index of asymmetry n with different inclination angle parameters Θ: a) q = 0.01; b) q=0.05
It is important to determine the optimal values of phase difference angles as well as the effect of deviations of these values from the optimal ones on the conveying velocity. The calculations show that the dependence of V on angle ε is displayed as a smooth curve in the region of maximum. So, inaccuracy in determining the values of optimal phase difference angles with an error of ±5-7° will lead to a slight decrease in conveying velocity. However, significant non-observance of optimal phase difference angles may lead to an essential decrease in conveying velocity and even to movement in the opposite direction.
6. CONCLUSIONS
Vibratory conveying of a material point, moving on an inclined track, that performs two-component vibration in non-hopping modes of particles moving when particles slide without detachment from the surface is considered. This vibration consists of harmonic longitudinal oscillations in the direction of conveying along the conveyor’s track and normal oscillations with piecewise constant acceleration in the direction perpendicular to the conveying surface. The effectiveness of the process of vibratory conveying can be estimated by the value of dimensionless velocity V, which determines the mean conveying velocity v divided by the frequency and amplitude of longitudinal oscillations. The dimensionless velocity V (conveying velocity) dependence on several dimensionless parameters is studied. These parameters are the inclination angle parameter Θ – tangent of inclination angle divided by the friction coefficient, the intense vibration parameter q – the ratio of the gravitational acceleration to the longitudinal acceleration amplitude, multiplied by the frictional coefficient, the index of asymmetry n – the ratio of the gravitational acceleration to the maximal acceleration of normal oscillations.
Dimensionless velocity V significantly depends on the phase difference angle ε, the optimal value of which (ε = εo) varies within 0 < εo < 90° and depends on the parameters Θ, q, and n. The equations for determining the optimal angle εo for three different non-hopping modes are obtained. The boundaries of the existence of these three modes, depending on the values of parameters Θ, q, and n, are determined.
Vibratory conveying by normal oscillations with piecewise constant acceleration provides an advantage in conveying velocity compared to conveying with normal polyharmonic oscillations, and this advantage increases with increasing the elevation angles.
For further research, it seems interesting to check the obtained theoretical results through experimental studies of two-component vibration conveying, both for normal oscillations with piecewise constant acceleration and for polyharmonic normal oscillations. It also seemsinteresting to create experimental vibratory devices with harmonic longitudinal oscillations and normal oscillations with piecewise constant acceleration to determine the possibility of their use in the industry.
