1. Introduction
Due to their attractive properties, wireless networks with distributed Medium Access Control (MAC) are being used more and more frequently, and this trend is likely to continue in the foreseeable future. A well-known example of such a network is a Wireless Local Area Network (WLAN), specified in IEEE 802.11 standard[1], which uses the Distributed Coordination Function (DCF) for distributed medium access. Other examples of distributed MAC networks include Wireless Sensor Networks (WSNs), Vehicular Ad Hoc Networks (VANETs) and Wireless Personal Area Networks (WPANs). Hence, a variety of distributed MAC protocols and various extensions of existing protocols have been proposed in the literature.
Most of the proposed protocols are based on the countdown-based medium contention used in DCF. In it, each transmission is preceded by a contention period divided into timeslots of predefined duration. At the beginning of contention, each competing station randomly selects a number called Backoff Counter (BC) from a predefined range. In each timeslot in which the channel remains idle, stations decrement their BCs by one, and the station that manages to decrement its BC to zero is the winner and starts transmitting. The other stations sense that the medium has become busy and freeze their BC countdown to be continued in the next medium contention. In addition to DCF, there is one more countdown-based contention method commonly used in distributed wireless MAC protocols, called the Enhanced Distributed Channel Access (EDCA). EDCA was first introduced in the IEEE 802.11e standard and is used mainly in MAC protocols based on this standard with the aim of providing Quality of Service (QoS) by differentiating traffic classes. The EDCA countdown is similar to DCF, but introduces a slight change in the countdown process: with DCF, stations decrement their BCs only in idle timeslots, but with EDCA a station decrements its BC by one even during a busy timeslot, i.e. during another station’s transmission. Although this change is seemingly irrelevant, it can lead to different network performance results, especially in heavily congested networks.
The performance characteristics of a wireless network, such as throughput, jitter and delay, depend on a complex set of parameters, including the number of active stations, data frame size, and channel quality. Thus, it is necessary to thoroughly analyze each proposed MAC protocol to understand its properties, determine the optimal set of parameter values for specific network scenarios, investigate ways to further improve protocol performance, and compare its performance with other MAC protocols. Two main methods for MAC performance analysis are simulations and analytical models. Computer simulations of the protocol under consideration allow researchers to accurately replicate the operation of competing stations in software, which provides very precise results compared to use of the real-world protocol. The main drawback of computer simulations is that they are time-consuming, especially when large number of different network scenarios need to be tested (e.g. when searching for an optimal set of MAC parameters for a particular network). In contrast, analytical models of MAC protocols rely on the mathematical abstraction of certain network characteristics through relatively simple equations, allowing for rapid evaluation of protocol behavior. This approach includes techniques like stochastic modelling, probability theory, queuing theory, and statistics. However, models of MAC protocols usually imply various approximations and simplifications. Before a specific model is used for MAC analysis, it must therefore be validated, usually by comparing it with simulation results.
The peculiarities of the EDCA countdown have long been recognized and taken into account in the modelling of the IEEE 802.11e MAC[2, 3]. More recent models of EDCA-based MAC protocols aim to represent a network more generally by omitting some of the usual assumptions. Examples include modelling a network with imperfect channel[4] or with unsaturated stations[5]. With the development of IEEE 802.11 standards and a variety of new MAC protocols proposed in the literature, new analytical models are being developed to enable performance analysis of MAC protocols in new network technologies[6, 7], and proposed extensions to the EDCA method[8, 9]. Since the EDCA countdown is often used in protocols that distinguish between different traffic types, there are several models of EDCA-based MAC protocols for vehicular networks[10, 11]. In[12], the network performance in error-prone channels is modeled, while[13] presents a model for a newly proposed EDCA-based protocol.
Recently, several wireless MAC protocols using a constrained priority freezing mechanism[14] have been proposed in the literature[15, 16]. The mechanism is an extension of the usual countdown procedure and can be combined with other contention methods, such as the sliding contention window[17]. It has been shown that the use of constrained priority freezing can increase throughput in congested networks, and that it can also be used for traffic differentiation[15]. An analytical model for using the protocol this mechanism and the DCF type of countdown has been developed[18], but no model exists when the EDCA type of countdown is used. Therefore, in this paper, a new model for a simple protocol that uses EDCA countdown and constrained priority freezing is developed and validated. The presented model assumes that all traffic belongs to the same class and should therefore serve as a basis for the development of a more complex model that includes traffic differentiation.
2. Related work
2.1 Medium contention in IEEE 802.11: difference between DCF and EDCA types of countdown
The IEEE 802.11 group of standards specifies two medium access control methods: collision-free centrally controlled access and distributed access based on medium contention. The former method is embedded in the Point Coordination Function (PCF), but this mode is optional and is rarely implemented in real-world devices. Thus, the latter method serves as the primary mode of media access in 802.11 wireless networks and is implemented as the Distributed Coordination Function (DCF). DCF is based on the Carrier-sense multiple access with collision avoidance (CSMA/CA) algorithm, in which each media transmission is preceded by a contention phase in which active stations compete for the rights to the medium. The aim of the contention is to determine a single active station that is allowed to transmit data. If two or more stations start transmitting at the same time, their signals collide, resulting in an unsuccessful transmission for the stations involved, and a waste of channel time. This situation is known as a collision. As the transmitting stations cannot detect the collision due to the high strength of their own signal, each data transmission should be followed by a short acknowledgment message (ACK) from the receiving station. If the transmitting station does not receive an ACK message after its transmission, it concludes that a collision has occurred and the transmission was not successful.
Although the different versions of the IEEE 802.11 standard introduce various minor changes to the media contention process, they are all based on the countdown mechanism and follow the same basic rules. Each competing station randomly selects a number from the range [0, W–1], called the Backoff Counter (BC) where W is called the Contention Window. A contention begins after the medium has been free for one Distributed Interframe Space (DIFS) time, when the stations start counting down their selected BCs. The contention is divided into timeslots (TS), and after each idle TS (when no transmission can be sensed) the stations decrement their respective BCs by one. If the medium is busy, a station freezes its current BC value for use in the following contention. A station wins access to the medium (i.e. it wins the contention) and starts transmitting when its BC value reaches zero. Therefore, the BC values represent the priorities of the station, where stations with lower BCs have higher priorities and Contention Window W defines a set of available priorities for each station.
It is obvious that there is a balance between the duration of contention (when a medium is not used) and the collision rate: a smaller contention window would result in shorter contention but more frequent collisions, while a very large contention window would result in few collisions but very time-consuming contention. To manage contention the size of the window, IEEE 802.11 uses the binary exponential backoff (BEB): after each collision, the stations involved double their contention window (up to the maximum size Wmax), and after each successful transmission, a station resets its contention window to the initial size W0. Thus, a collision is used as a sign of network congestion and causes the stations that were affected by the collision to double their contention windows, to reduce the probability of selecting the same BC as another station in the network.
The BC countdown mechanism explained above is not only used in wireless local area networks, but also forms the basis for many other distributed wireless MAC protocols, such as vehicular ad hoc networks (VANETs), personal area networks (PANs), wireless sensor networks (WSNs), etc.
In 2005. the IEEE published the 802.11e amendment to the standard[19] with the aim of categorizing data traffic and providing a higher probability of transmission for high-priority data. This is achieved through a method of media access called Enhanced Distributed Channel Access (EDCA). Contention is still based on the BC countdown, but EDCA introduces four traffic classes, with each class using its own set of parameters during media contention, namely the initial contention window W0, the maximum contention window Wmax, and the duration of the inter-frame space (called AIFS –Arbitration Inter-Frame Spacing). By using smaller values for these parameters, data belonging to higher-priority traffic has a higher chance of (successfully) accessing the medium than lower-priority data. However, EDCA also introduces a subtle change to the countdown mechanism that is often overlooked in the literature: a competing station decrements its BC by one at the beginning of a timeslot, rather than at the end of an idle timeslot. This means that in the EDCA variant of the countdown, the stations decrement their BCs by one even in busy timeslots, when one or more stations transmit their data.
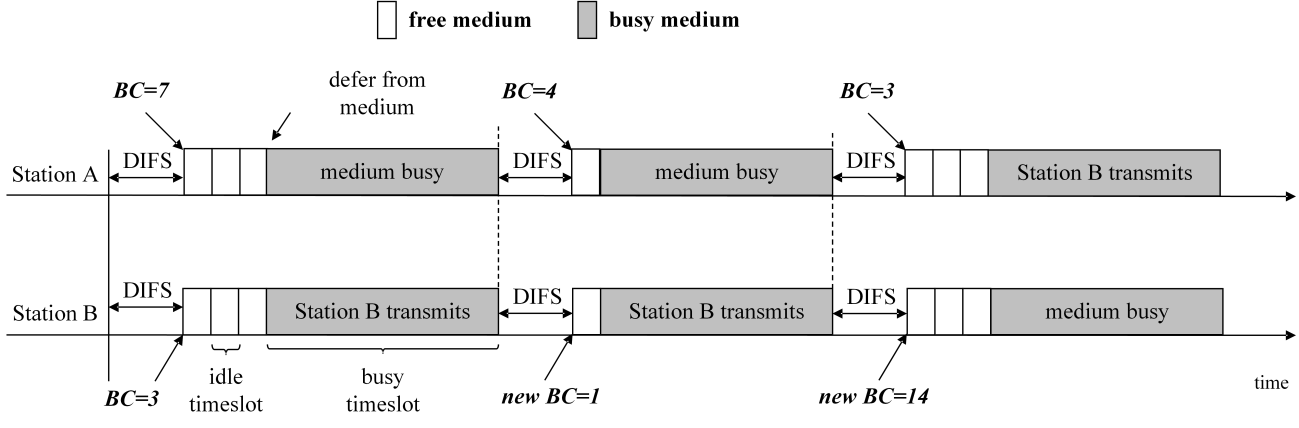
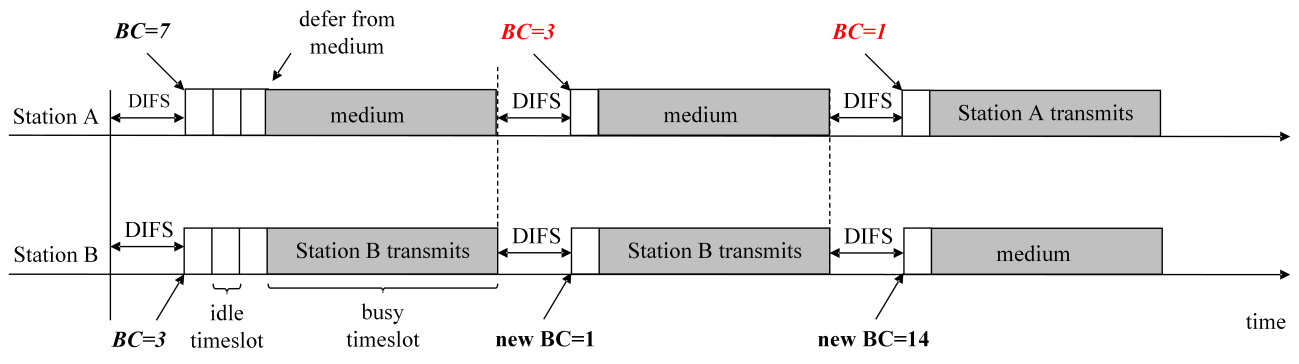
The difference in the countdown procedure between DCF and EDCA is illustrated in Figure 1. The figure shows three consecutive contentions between two active stations, A and B, which decrement their BCs according to the DCF and EDCA countdown in Figure 1, a and b, respectively. In both examples, the stations enter the first contention with BC(A) = 7 and BC(B) = 3. Station B wins after 3 idle timeslots, sends data, and enters the second contention with a new, randomly selected BC(B) = 1. However, after losing in the first contention, station A enters the second contention with a different value of BC(A), although in both cases it lost the contention after 3 idle timeslots. This is because in the case of the EDCA countdown, station A decrements its BC value by one during the transmission of station B. The same difference between DCF and EDCA countdowns is seen in the second contention and the subsequent transmission: EDCA station A enters the third contention with a BC decremented by 2, while DCF decrements the BC by only 1 compared to the beginning of the second contention. As a result, the third contention takes 3 timeslots in the example with DCF stations, and only 1 timeslot in the case of EDCA stations.
Although the difference between the DCF and EDCA countdown process may seem trivial, it can lead to a significant disparity in protocol performance. One can conclude that the EDCA type of countdown provides a faster countdown of randomly selected BC values compared to the DCF countdown. This leads to a shorter duration of contention, but higher collision rates, especially in heavily congested networks[20].
a) DCF type of countdown
b) EDCA type of countdown
Fig. 1 The difference between a) DCF and b) EDCA countdown
2.2 Constrained priority freezing mechanism
A station that loses media contention freezes its current (decremented) BC value and uses this value for the next contention. Thus, once a station randomly selects its BC value, this BC value is decremented through one or more successive contentions until it finally reaches zero and the station wins access to the medium. Only after the transmission does a station randomly select a new BC. In[14], constrained priority freezing is proposed, which is an extension of the standard countdown-based contention method. The main idea of this mechanism is to limit the number of consecutive contention losses a station can suffer before it is forced to abandon its current BC value. This is achieved by introducing a new parameter called the freezing limit (FL): if a station loses a medium contention in FL+1 consecutive contentions after randomly selecting its BC, it may not freeze its current BC and use it in the next contention. Instead, it must select a new BC from its current Contention Window. To keep track of the number of lost contentions, each station maintains a variable called the Freezing Counter (FC), which is incremented by one each time a station loses a contention, and is reset to zero when it selects a new BC (due to winning the medium access or exceeding the freezing limit). While in[14] the mechanism is embedded as part of the MAC in 802.11-based WLANs, it can also be used in other wireless networks that employ countdown-based contention as a method to control media access.
Since it has been shown that the constrained priority freezing mechanism can lead to a reduction in collision rate, it has since been used as part of several other protocols proposed in the literature[15],[16].
2.3 Modelling of contention-based wireless MAC protocols
Analytical models of countdown-based wireless MAC protocols are usually based on a multi-dimensional Markov chain, which is used to represent the behavior of a single contending station. Each state of the chain represents a particular combination of the values of the MAC parameters that define the current operational state of the station. In successive discrete times, a station changes from one state to the next with a certain probability. The states in a chain usually represent different values of BC, BEB stage, channel status during the previous timeslot (idle or busy), probability that the station has no data to transmit, and so on. Such a chain makes it possible to analytically represent the operation of an observed station. Assuming that all active stations operate in the same way and the transition probabilities of the Markov chain are constant, important statistics can be derived for the entire network, including throughput, collision probability, duration of contention, packet delay, etc.
The Markov chain as a basis for modelling wireless MACs was first used in Bianchi’s seminal work[21], which analyzes the performance of a saturated one-hop DCF WLAN network. Bianchi’s work is widely cited (over 6500 citations) and serves as the basis for many other published models of various proposed wireless MAC protocols. These models usually omit one of Bianchi’s assumptions, such as the introduction of retransmission retry limit, unsaturated stations, channel errors, hidden stations, or differentiated data priorities[3]. It is understandable that, with the development of the 802.11 standard and the deployment of wireless networks in emerging new areas, new models for corresponding protocols have been developed[22].
Although often neglected, the difference between the DCF and EDCA type of countdown has also been recognized in the published models of various MAC protocols. The first model that takes into account the peculiarities of the DCF countdown (namely the freezing of BC at the beginning of a busy timeslot) is presented in[23], where two different transmission probabilities are assigned to the timeslot, depending on whether the previous timeslot was idle or busy. Finally, the Bianchi’s original model has been updated to reflect the real nature of the IEEE 802.11 DCF function[24]. Similarly, models for protocols using the EDCA type of countdown use different Markov chain transition probabilities to more accurately reflect this particular countdown mechanism.
In[18], a mathematical model for a basic constrained priority freezing mechanism is presented. In[16], a protocol using the constrained priority freezing mechanism is proposed for use in Industrial Wireless Networks (IWNs) and a model for such a protocol is developed. However, both models assume a DCF countdown type. Currently, there is no model for the EDCA type of countdown for protocols that use a version of the constrained priority freezing mechanism.
3. Model of protocol using EDCA type of countdown and constrained priority freezing
In this section, we develop a model for a one-hop network with n active competing stations that use the constrained priority freezing mechanism and the EDCA countdown (i.e. decrement their BCs by one in both idle and busy timeslots). The flowchart for such a protocol is shown in Figure 2.
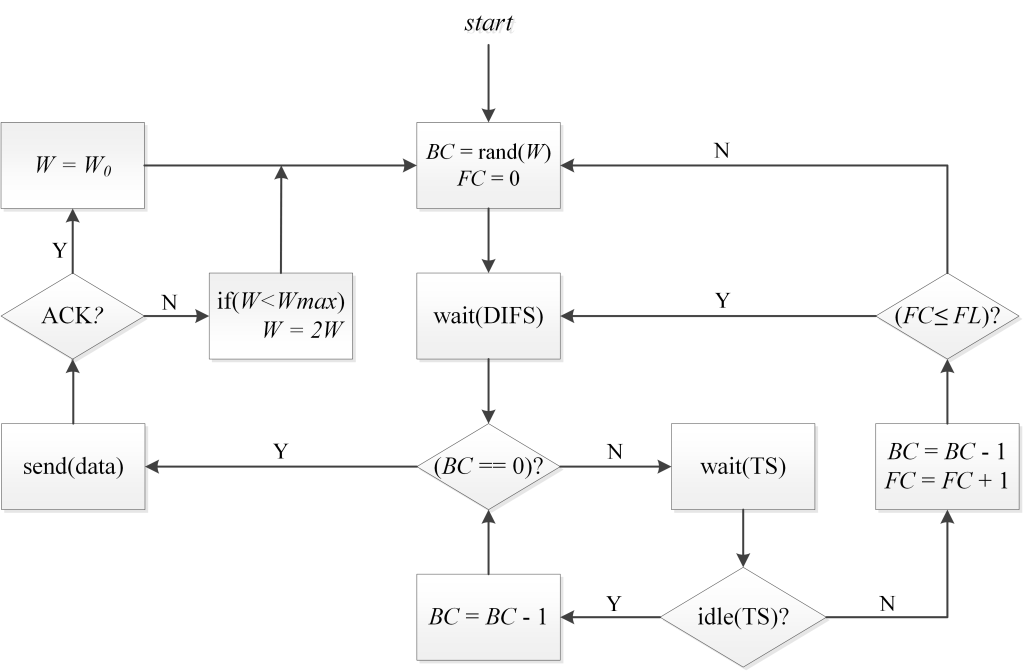
Fig. 2 Flow diagram of the modeled MAC protocol with EDCA countdown and constrained priority freezing
The main assumption in our model is that the conditional probability T that the observed transmitting station suffers a contention loss is constant for all timeslots and independent of the current contention window size of the station. This is the probability that at least one of the (n–1) remaining stations starts transmitting in the random timeslot under consideration. Since we assume that the probability T is constant for all stations and timeslots, the probability that the observed station suffers a contention loss while its BC is greater than zero is also constant and equal to T. The validity of this assumption has been proved in[25] and[26]. In addition to the main assumption, we assume that:
the channel is ideal, i.e. there are no channel errors (collisions are the only cause of unsuccessful transmissions),
there is no retransmission retry limit, i.e. the number of retransmissions is unlimited,
active stations are saturated, i.e. they always have new data to send,
the timeslots are synchronized for all stations,
ACK timeouts and EIFS times are ignored,
all traffic belongs to the same traffic class.
The last assumption means that we do not aim to model IEEE 802.11e MAC, since the standard includes four different traffic classes, each with its own set of contention parameters. However, the model presented in this paper can serve as a first step in developing such a model, or in developing a model for any other MAC protocol that includes the EDCA type of countdown and constrained priority freezing.
In the model, the operation of a single observed competing station is modeled using a three-dimensional Markov chain, where each dimension is used to represent modifications of a particular parameter during media contention:
the first dimension is used to represent the BEB process of the station, i.e., the doubling of its contention window after experiencing a collision and the reset to the minimum initial value after a successful transmission
the second dimension is used to represent the BC management of a station, i.e. its random selection and decrementation
the third dimension is used to represent the incrementing of the FC by a station after a loss of contention and reset of the FC to zero after exceeding the freezing limit
Therefore, at any time of the station’s activity, its state is represented by the triplet {s, i, j}, where:
s represents the BEB stage of the station that defines the size of its contention window: Ws = W0∙2s, 0≤ s ≤m, Wmax = W0∙2m;
i represents the value of the BC of the station in the current timeslot, i ∊ [0, Ws−1];
j represents the value of the FC of the station in the current timeslot, j ∊ [0, FL].
The resulting Markov chain model for the operation of a single station is shown in Figure 3. Due to the complexity of the model, Figure 3a depicts the transitions within a single BEB stage, while Figure 3b shows the transitions between the states of different stages.
For better readability, the first coordinate in the states of Markov chain has been omitted in Figure 3a. Since only transitions in a single, generic BEB stage are shown in Figure 3a, the first coordinate should simply be s in all states shown. Certain states in each BEB stage are highlighted in color in Figure 3. The green-shaded states are those where a station’s FC equals FL: if a station loses the contention in one of these states, it must select a new BC from the current contention window to be used in the next contention. The red-shaded part of each BEB stage represents the “initial” states of the station, i.e. those states with j = 0. After the random selection of the BC, a station must be in one of these states. As in Figure 3a represents the probability that the station enters one of these states in the BEB stage s due to the random selection of a new BC. In other words, As is the sum of the probability sels and the probability that the station selects a new BC from stage s after transmission (after successful transmission for s=0, and after a collision for s>0). The blue-shaded part in Figure 3a represents the winning states of the station, i.e. the states with i = 0. After reaching one of these states, the station begins its transmission. Each transmission has the probability of success (1–T), and the probability of collision T. In the case of success, the station enters one of the initial states of BEB stage 0. If, on the other hand, the station experiences a collision, it enters one of the initial states in the next BEB stage. An exception is the last BEB stage m (with Wm = Wmax = W0∙2m): after transmitting from this stage and experiencing collision, a station returns to one of the initial states of the same stage m.
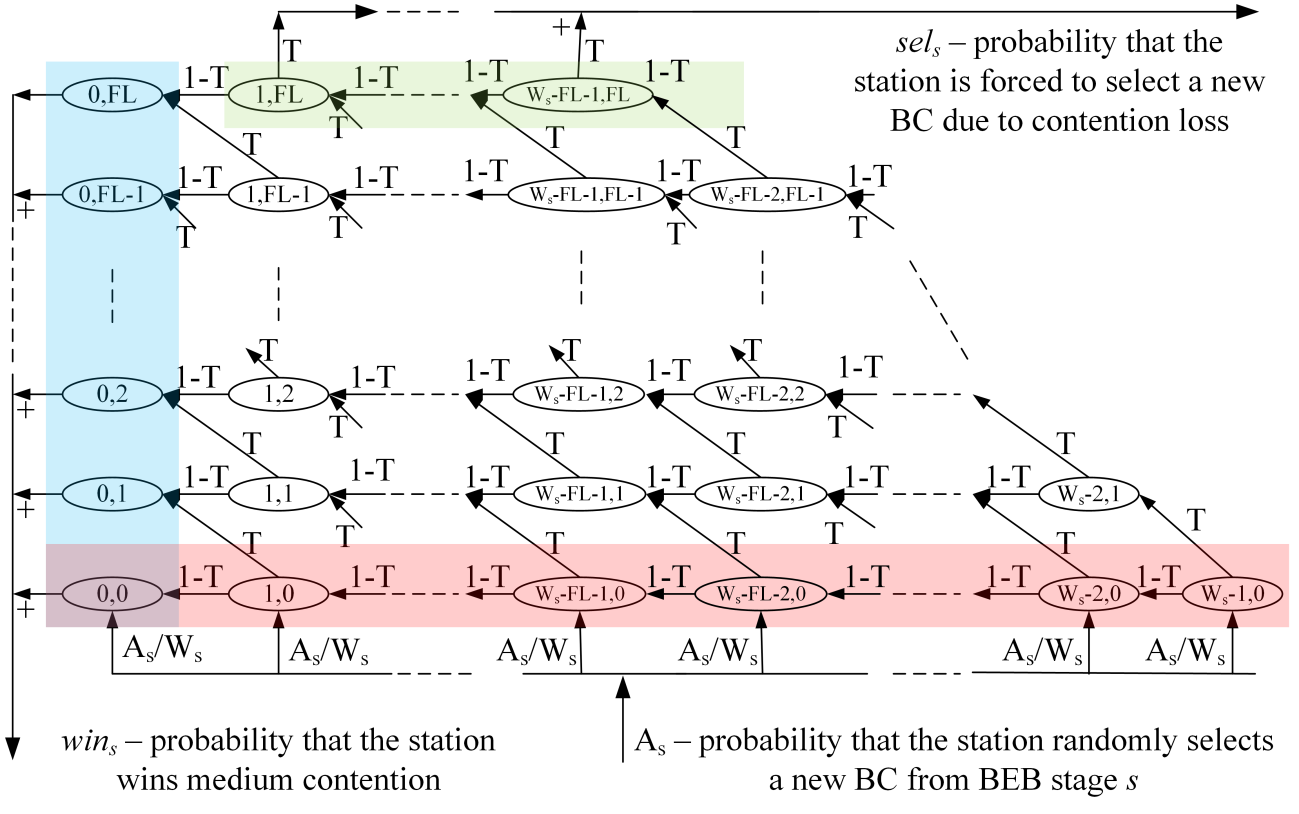
a) Transitions within a single BEB stage
b) Transitions between BEB stages
Fig. 3 Markov chain representing the operation of a single station
Let us adopt the notation P{s1, i1, j1 | s0, i0, j0} = P{s(t + 1) = s1, x(t + 1) = i1, y(t + 1) = j1 | s(t) = s0, x(t) = i0, y(t) = j0}. The probabilities for the one-step transition in the chain are given with:
The probabilities of all other one-step transitions are equal to zero. Here, T represents the conditional probability that the observed transmitting station experiences a collision. Correspondingly, (1–T) is the conditional probability that the observed transmitting station experiences a successful transmission.
Analysis of the presented Markov chain is done in two steps:
first, by analyzing the transition probabilities for the part of the Markov chain that represents a single BEB stage, the probabilities of all states belonging to the same stage are expressed as a function of the probability of a single state {s, Ws–1, 0};
then the probabilities of all states (including all BEB stages) in the chain are expressed as a function of the probability of a single state {s, Ws–1, 0}.
Afterwards, the probability τ that a randomly selected station starts transmitting in a randomly selected timeslot can be obtained. From this, various performance metrics for the entire network are calculated, such as collision probability, the average contention duration and the network throughput.
Let bs,i,j= limt→∞ P{s(t) = s, i(t) = i, j(t) = j} be the limit distribution of our Markov chain. Due to the properties of the chain, this is the same as the stationary distribution. One should note that not all states {s, i, 0} have the same probability: the state {s, Ws, 0} can only be reached by randomly selecting a new BC (either after the transmission or because too many consecutive contention losses occur and the freezing limit is exceeded), while all other states {s, i, 0} can be reached by randomly selecting new BC = i or by selecting a large BC and counting down to i without experiencing contention loss. Thus, the probabilities of these states can be expressed as:
(1)
where As represents the probability that a station is forced to randomly select a BC from the contention window Ws. Thus, for all states {s, i, 0}, the steady-state probability can be written as:
(2)
For states {s, i, j>0}, the probabilities are given with:
(3)
since these states can be entered in two ways: either by reducing BC during an idle timeslot (with probability 1–T), or by reducing BC and incrementing FC during a busy timeslot (with probability T). The transition to the state {s, i, j>0} is only possible if the previously selected BC value satisfies the condition BC = x ≥ i + j. In this case, the probability of entering the state {s, i, j>0} is equal to the probability that the station loses medium contention (i.e. senses a busy timeslot) j times and experiences an idle timeslot (x–i–j) times in (x–i) consecutive timeslots following BC selection. Let ps,x,0→s,i,j denote the probability that a station, starting from the state {s, x, 0} after random selection of BC = x reaches the state {s, i, j} without selecting a new BC between these two events:
(4)
In this expression, the binomial coefficient represents the number of different trajectories from the state {s, x, 0} to the state {s, i, j}, with each of them having probability Tj∙(1–T)x–i–j. The probability of steady state {s, i, j} can now be expressed as the sum of all the probabilities of all possible trajectories that can lead to this state after the selection of a new BC in the BEB stage s:
(5)
After substituting k = x–i–j and As/Ws = bs,Ws–1,0 we get:
(6)
Therefore, the probabilities of all other states in the BEB stage s are now expressed as a function of the probability of the state {s, Ws–1, 0} and of the probability T that the observed station loses media contention in a randomly selected timeslot.
In the next step of the Markov chain analysis, the probabilities of each state {s, Ws–1, 0}, s ∊ [0, m], are given as a function of the probability of state {0, W0–1, 0}. This also means that the probabilities of all states are indirectly specified as a function of the probability of this state.
Let Gs be the probability that a station in BEB stage s must select a new BC due to its FC exceeding FL, and let this probability be expressed in units of the probability of state {s, Ws–1, 0}. The probability Gs can be calculated as the probability that a station enters one of the states {s, i>0, FL} and then experiences a busy timeslot:
(7)
From Eq. (6), Gs can be expressed as:
(8)
Furthermore, let αs be the probability that a station in BEB stage s wins the media contention, but experiences a collision, also expressed in units of the probability of state {s, Ws–1, 0}. In other words, αs is the probability that a station in BEB stage s completes its BC countdown (i.e. reaches one of the states {s, 0, j}) in the same timeslot as one or more other active stations:
(9)
Using Eq. (6), αs is calculated as:
(10)
A state {s, Ws–1, 0}, where 0 < s < m, can be reached in two ways:
by counting BC down to zero in BEB stage s−1, winning the contention and a collision occurring,
by experiencing FL+1 consecutive contention losses since the last BC selection while in BEB stage s.
Therefore, the probability of entering the state {s, Ws–1, 0} is given by:
(11)
From this, the probability of state {s, Ws–1, 0} can be calculated as:
(12)
The expression for the probability of state {m, Wm–1, 0} is somewhat different, because this state belongs to the last BEB stage, so it can also be reached by experiencing collision when transmitting while in stage m. Therefore:
(13)
Finally, probabilities of all states {s, Ws–1, 0}, s>0, can be expressed as a function of the steady-state probability of {0, W0–1, 0}:
(14)
(15)
Of course, the sum of probabilities of all states in the chain must be equal to 1:
(16)
In these equations, the state probabilities depend on the conditional probability T, in turn depends on the probability τ that the observed station starts its transmission in a randomly selected time slot (i.e. wins in medium contention):
(17)
where n is the number of competing stations, and (1–τ) is the probability that one of the remaining (n–1) stations does not start its transmission in the timeslot under consideration. The probability τ in turn is a function of T, since there is the probability that the observed station is in one of the transmitting states in which its BC is zero:
(18)
The probability T is a strictly increasing function of τ, while τ is a strictly decreasing function of T. Therefore, these two functions have a unique intersection point. As usual with more complex Markov chain models of the observed station[24], our model does not provide a closed-form solution, but the set of our nonlinear fixed-point equations can be solved quickly using typical numerical methods.
The numerical solution of Eqs. (14)–(18) is beyond the scope of this paper, but it should be noted that we used a simple fixed-point iteration and that the number of iterations required to determine the probability τ with the accuracy of 10–12 is less than 50 in the worst case. On a computer with Intel Pentium G2030 3 GHz CPU and 8 GB RAM, the time required to numerically determine the values of τ and T for 288 different network scenarios is less than 10 seconds.
After obtaining the probability τ, various network statistics can be determined, of which the network throughput is usually the most important. Throughput is measured in bits per second (bps, b/s) and indicates the amount of data successfully transmitted per unit of time.
The probability that a random timeslot is idle, from the channel point of view is equal to the probability that none of the n active stations transmits in a timeslot under consideration:
(19)
Of course, the probability that the observed timeslot is busy is also given with:
(20)
These are timeslots that contain either one transmission (timeslot contains a successful transmission) or more than one transmission (timeslot contains a collision of two or more simultaneous transmissions). The probability that a timeslot contains a successful transmission is equal to the probability that exactly one station transmits in the timeslot under consideration, while none of the other (n–1) stations transmit:
(21)
Therefore, the probability that a timeslot contains a collision is given with:
(22)
The probability that a busy timeslot contains successful data transfer is equal to:
(23)
while Pc = (1–Ps) represents the proportion of busy timeslots that contain collisions. The expected contention duration, expressed in idle timeslots, can be calculated as follows:
(24)
Finally, the network throughput can be determined as the ratio of the average amount of data successfully transferred per busy timeslot and the average duration of contention and busy timeslot:
(25)
where:
avgDataSize is the average size of the transferred data frames (for simplicity, in this paper we assume that all data frames in the same scenario are the same size),
TSdur is the duration of an idle timeslot (depends on the version of the 802.11 standard),
SuccDuration is the average duration of a successful transmission and includes the time needed required to transmit the data frame, the DIFS and SIFS times, and the duration of the recipient’s acknowledgement message (depends on the frame size and the version of 802.11 standard),
ColDuration is the average time the channel is busy during a collision and includes time required to transmit the collided data frames as well as the DIFS and EIFS times (depending on the size of the largest frame in the collision and the version of the 802.11 standard).
The method used in this paper to calculate the throughput is a derivation of the method presented in[21].
4. Model validation
To validate the proposed model, its results are compared with the results obtained when simulating a network of stations with EDCA countdown and constrained priority freezing. A custom simulation tool was written in MATLAB, focusing on the MAC-level performance of the protocol to avoid influences that higher levels within the protocol stack might have on the results. Additionally, the custom simulator is faster than the usual simulators used in the literature, such as “ns-3”[27], and allows easy and detailed extraction and display of results. A single-hop ad hoc network with n saturated stations was simulated. The simulation time was measured in idle timeslots. Each network scenario was executed 10 times and lasted 1 million timeslots. Only the data of the last 0.9 million timeslots were considered to capture the steady-state condition results. The different scenarios are created by changing the following parameters:
number of active stations n: 3 to 50;
freezing limit FL: 0 to 20;
transmitted frame sizes: 290 B, 1040 B or 7280 B (corresponding to 7 aggregated frames);
initial window size W0: 16 or 32;
set of network parameters, such as interframe time durations and channel data rates, in accordance with the 802.11g and 802.11n standards, as shown in Table 1.
In total, the model results were evaluated in almost 300 different network scenarios.
Table 1 Network parameters used for model validation
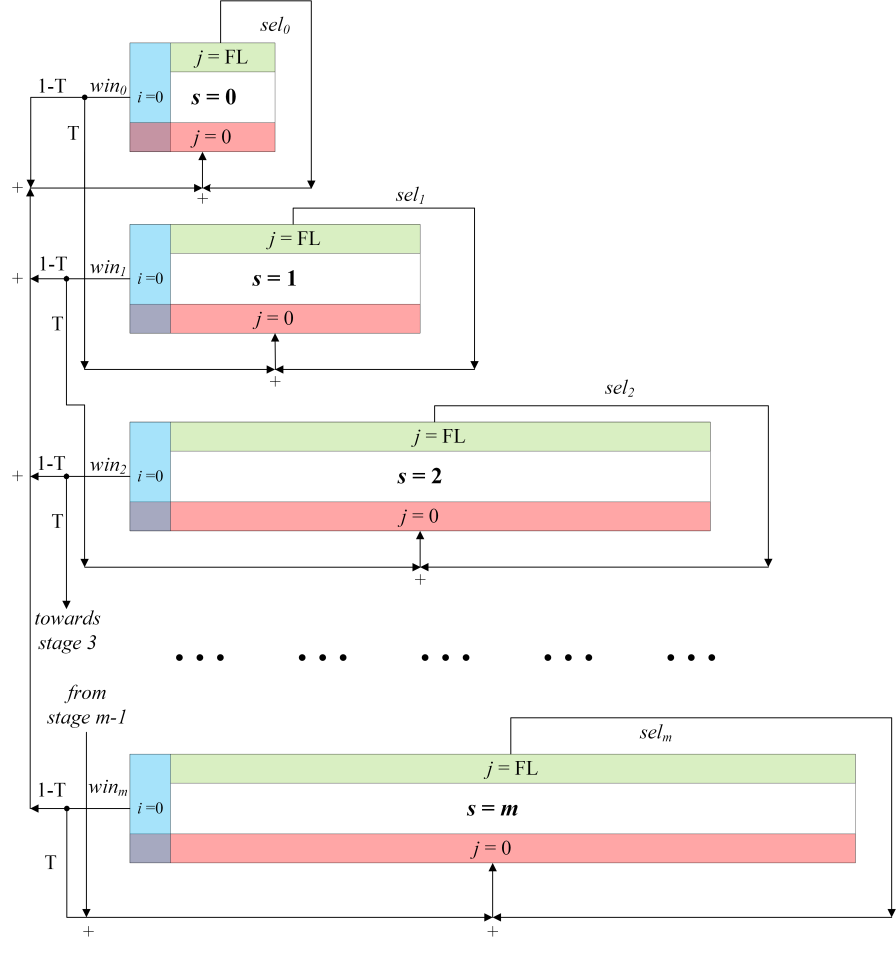
The main goal of Markov chain analysis is to determine the probability τ that the considered station starts transmitting in a random timeslot since the further network properties are calculated from this probability. Thus, in the first step of the model validation, we compare the probability τ in the model and in the simulations. Figure 4 shows the probability τ calculated from the model and obtained from simulations for two initial window sizes W0. The probability τ is shown as a function of the FL, from FL = 0 to FL = 20. The model results are shown as lines, and simulation results as dots, for different numbers of active stations (n = 3, 6, 10, 20, 35, 50). As can be seen, the model produces the largest errors for small networks (n = 3, 6) with a small freezing limit (FL = 0, 1, 2), where the relative error of the model reaches up to 4%. However, for all other scenarios (including small networks with FL ≥ 3), the relative error of the probability τ determined by the model is less than ±1% when compared to the simulations.
The accuracy of the model decreases in small networks because our assumption that the probability T (that the observed station loses medium contention) is independent of the BEB stage of the station loses validity. Consider a case where the observed station is in an advanced BEB stage (s > 0). This means that a collision has occurred and at least one other station has also doubled its contention window. In a small network with only three competing stations, only one station remains with an initial contention window W0, selecting small BC values, while the other two stations (the observed one and its collision partner) use larger contention windows, select on average larger BCs and have a lower chance of winning the medium in the following contention(s). In such a situation, only one station in the entire network has the right to select small BCs on average and the model incorrectly predicts that the probability of losing the media contention is the same as in a situation where the observed station uses the initial window. This is emphasized for networks where stations use small FLs, as they are less likely to count down their selected BCs to zero due to the highly constrained priority freezing. Therefore, the model overestimates the probability that the observed station starts transmission in a randomly selected timeslot, causing errors shown in Figure 4.
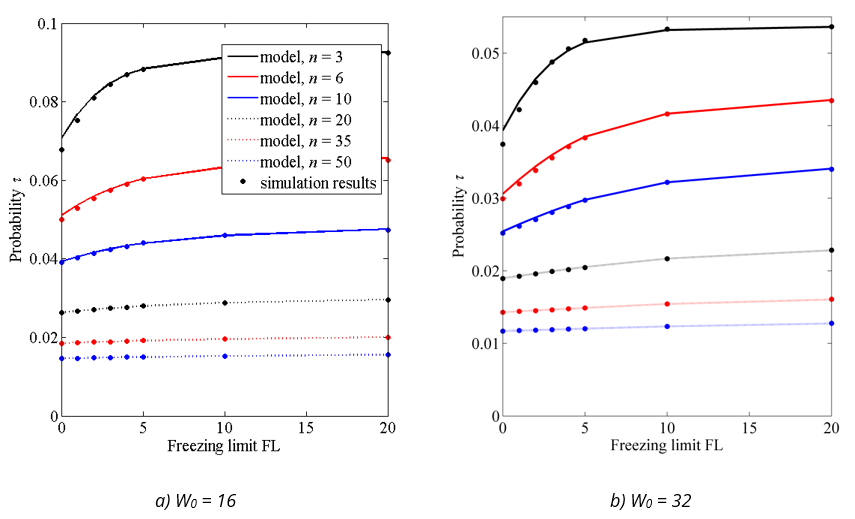
Fig. 4 Probability τ, comparison of model and simulation results for W0 = 16 (a) and W0 = 32 (b)
Now we evaluate the accuracy of the model in predicting the network throughput, calculated using Eqs. (19)–(25). The throughput depends not only on the contention parameters, such as initial window and FL, but also on all the parameters listed in Table 1 and on the sizes of the transmitted frames. To cover different scenarios, Figure 5, Figure 6 and Figure 7 show the results for three different cases:
low data rate and large frames (802.11g parameter set, 1040 B sized frames),
low data rate and small frames (802.11g parameter set, 290 B sized frames),
high data rate and aggregated frames (802.11n parameter set, aggregation of 7 1040 B sized frames).
The throughput is expressed as a fraction of channel bandwidth and shown as a function of the freezing limit for 3, 6, 10, 20, 35 and 50 active stations.
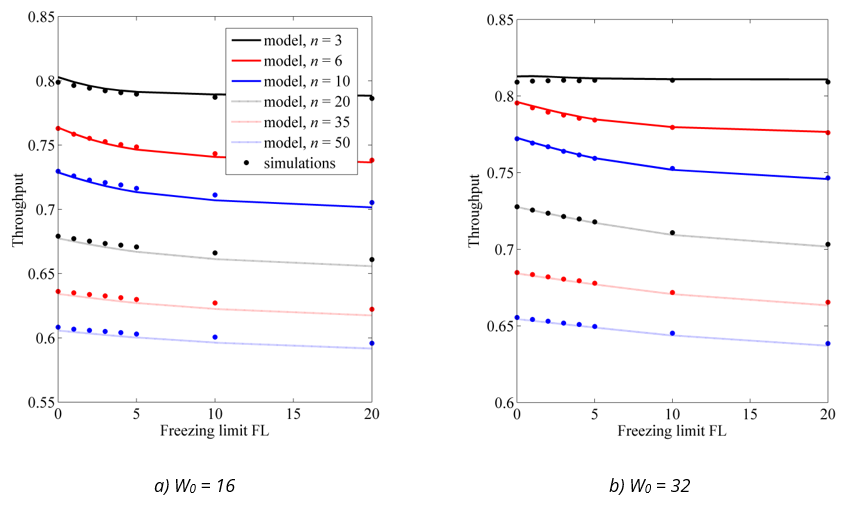
Fig. 5 Comparison of network throughput from the model and simulations for low data rate and large data frames (a) W0 = 16 (b) W0 = 32
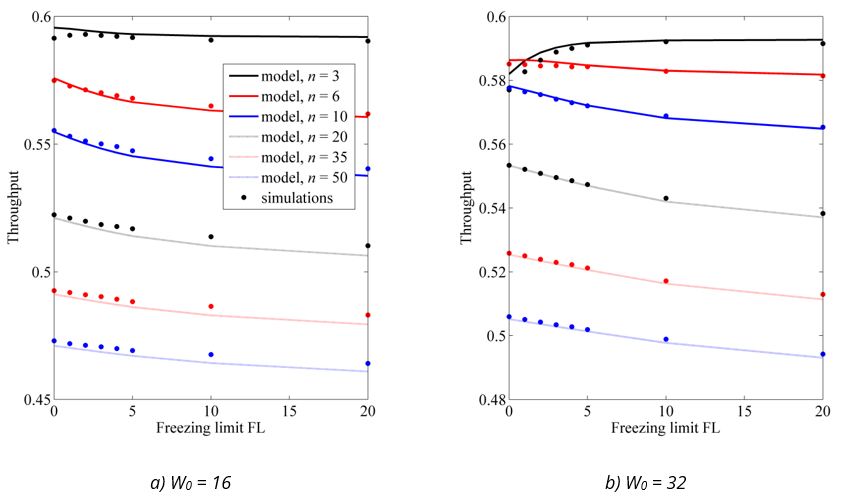
Fig. 6 Comparison of network throughput from the model and simulations for low data rate and small data frames (a) W0 = 16 (a) W0 = 32
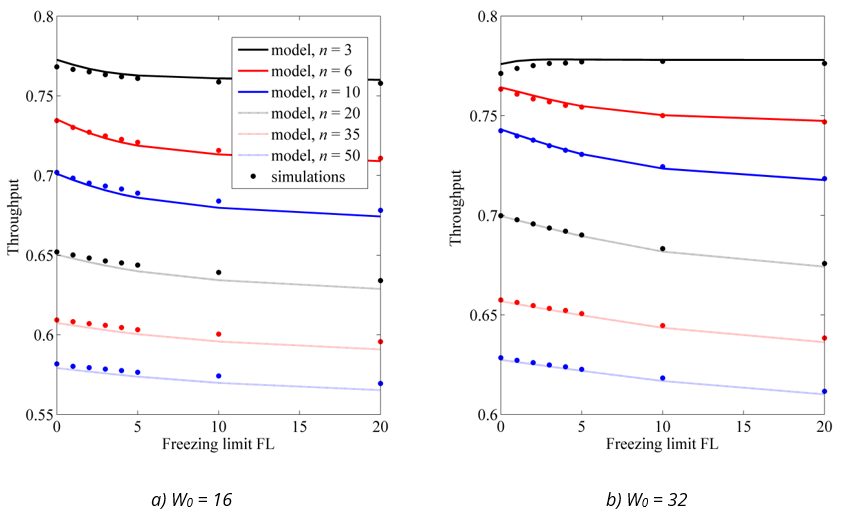
Fig. 7 Comparison of network throughput from the model and simulations for high data rates and aggregated data frames (a) W0 = 16 (a) W0 = 32
The model is very accurate in predicting the network throughput for all cases considered. The model results deviate from the simulation results by less than ±0.8% in all scenarios. This even applies to small networks with highly constrained priority freezing. This is because most of transmissions in such networks are successful: the model overestimates the collision rate (due to the overestimation of the probability τ), but the transmissions are overwhelmingly successful, which reduces the impact of an incorrect estimate of the collision rate on the overall throughput results.
It should be noted that the time required to run all simulations is measured in hours, as opposed to seconds for computing the model results.
5. Conclusion
In this paper, we presented a new model for a wireless network protocol in which competing stations use the EDCA countdown enhanced with the constrained priority freezing mechanism. A single hop network with saturated stations was considered and traffic differentiation was ignored. The model is based on a three-dimensional Markov chain used to represent the operation of a single active station. From the chain, the probability that the station accesses the medium in a random timeslot is determined using numerical techniques. This probability is then used to calculate various network characteristics, in particular the network throughput.
The model is validated by comparing its results with simulation results in almost 300 different network scenarios. The scenarios are designed by varying the initial contention window sizes, data frame sizes, number of active stations and channel data rates. The model is highly accurate in predicting the network throughput: the relative difference between the throughput calculated with the model and the throughput determined in simulations is not greater than 0.8% in any of the scenarios considered.
The model presented is the first to accurately predict the characteristics of the network when EDCA countdown (as opposed to DCF countdown) is paired with constrained priority freezing. As such, the model can serve as a basis for modelling and analyzing modern wireless MAC protocols that incorporate additional mechanisms, such as different traffic classes, multi-hop networks, or another variant of the countdown-based wireless MAC standard. By assigning different freezing limit values to different traffic classes, further traffic differentiation could be achieved. This is particularly important for future networks in which time-critical data are to be transmitted, such as ad hoc vehicular networks. Since constrained freezing offers increased throughput in heavily congested networks, the model presented could also be used to analyze the performance of future MAC protocols for dense networks.
