INTRODUCTION
Nowadays, firms with different types of profitability are facing financial problems in the sense that they are missing financial funds for the realization of projects which will increase their value. Therefore, a firm needs to find an investor who will secure needed funds. In the perfect world, investors should invest in all projects whose return is bigger than the return of an alternative investment with an alternative rate of return. The imperfection of a relationship between a firm and an investor is described as information asymmetry, which causes a lot of attractive projects to fail due to the lack of financing. Because of that, this problem has significant economic implications and the question is being raised about a type of contract between a firm and an investor which will ease the consequences of information asymmetry. In designing the contract, it must be considered that an investor is usually not aware of information about the profitability of a firm or the value of the project. In the literature, this problem was faced in different ways. Leland and Pyle[1] are describing a signaling model in which the information about a project’s quality is known only to an entrepreneur, and are showing how the willingness to invest, is a signal about a project’s quality. Bhattacharya[2] follows this approach in his analysis of dividends as signals and draws interesting comparatively static results. Myers and Majluf[3] analyze a model in which a manager has information about a value of a firm and a net present value of an investment. The firm can be in two different states and the sum value of the firm is divided into new and old shareholders depending on the market value of the firm, the intrinsic value of the firm, and the investment. Gibbons[4] is assuming that a project value is a common knowledge, but, unlike the analysis of Myers and Majluf, Gibonns analyses the whole specter of equity shares that a firm can offer to an investor. He is describing the concept of perfect Bayesian equilibrium and in a signaling game of a firm and an investor presents conditions under which there is the existence of a pooling or a separating equilibrium in a model with two types of a firm. Forges and Renault[5] are dealing with the concepts of equilibriums, especially the perfect Bayesian equilibrium, which is needed for the analysis of the more complex games. A signaling game is a dynamic game with incomplete information, and for the analysis of that type of game, knowledge about the Bayesian formula and conditional probability[6] is needed. Also, Bergemann and Morris[7] are covering both topics, the concept of equilibriums and the Bayesian formula, in their work about games with incomplete information, while Bergh, Ketchen, and others[8] talk about information asymmetry in the management practice. On the same track is Oskar Colombo[9] with his work about signaling as a way to overcome information asymmetries and reduce the uncertainty while in the search for fresh capital. Chandra[10] is solely focused on investment and management portfolio, and approaches the subject from a finance domain standpoint. Gibbons [4; p.207] states that a separating equilibrium always exists in the signaling game of a firm and an investor. In this article, it is shown that this result is incorrect. The signaling game in the article is shown graphicly so the clear order of moves and payoffs is visible. In the comprehensive analysis, it is clearly stated for which probabilities of the firm’s types exist either the separating or the pooling equilibrium. The results shown in the model with the two types are generalized in the extended model with the three types of firms. The function that describes the lowest equity stake which a rational investor would accept when he creates a belief about a type of firm is shown both graphicly and analytically, along with her properties. The analysis of level lines of the lowest equity stake function enables to differentiate cases and to describe the equilibrium. The contribution is reflected in a visual display of conditions under which there is the existence of the pooling, the semi-pooling, and the separating equilibrium in the model with three types of firms. In practice, especially in capital markets, it is usual that a relationship between a firm and an investor is characterized by information asymmetry. The firm’s situation is clear due to superior information and rational strategy is easy to find. However, in a perfect Bayesian equilibrium, the investor’s strategy needs to be in accordance with a created belief about which type could have sent the signal. Therefore, practical use of a concept for an investor willing to invest money in a capital market would be to create a belief and make a rational choice based on the frequency of occurrence of each type of firm in a market and his knowledge about a market. It is important to highlight that a firm should anticipate the behavior of an investor in order to be sequentially rational. That being said, the model with three types is more precise than a model with two types because it is more realistic to expect a higher diversity of firms in a market. After the introduction, the article is revising Gibbon’s model with two types of firms and the stated results are being reviewed. In the chapter that follows model is being expended from the two to the three types of firms and conditions under which there is the existence of the pooling, the semi-pooling, and the separating equilibrium, are being derived and shown both graphicly and analytically.
THE MODEL WITH TWO TYPES OF FIRMS
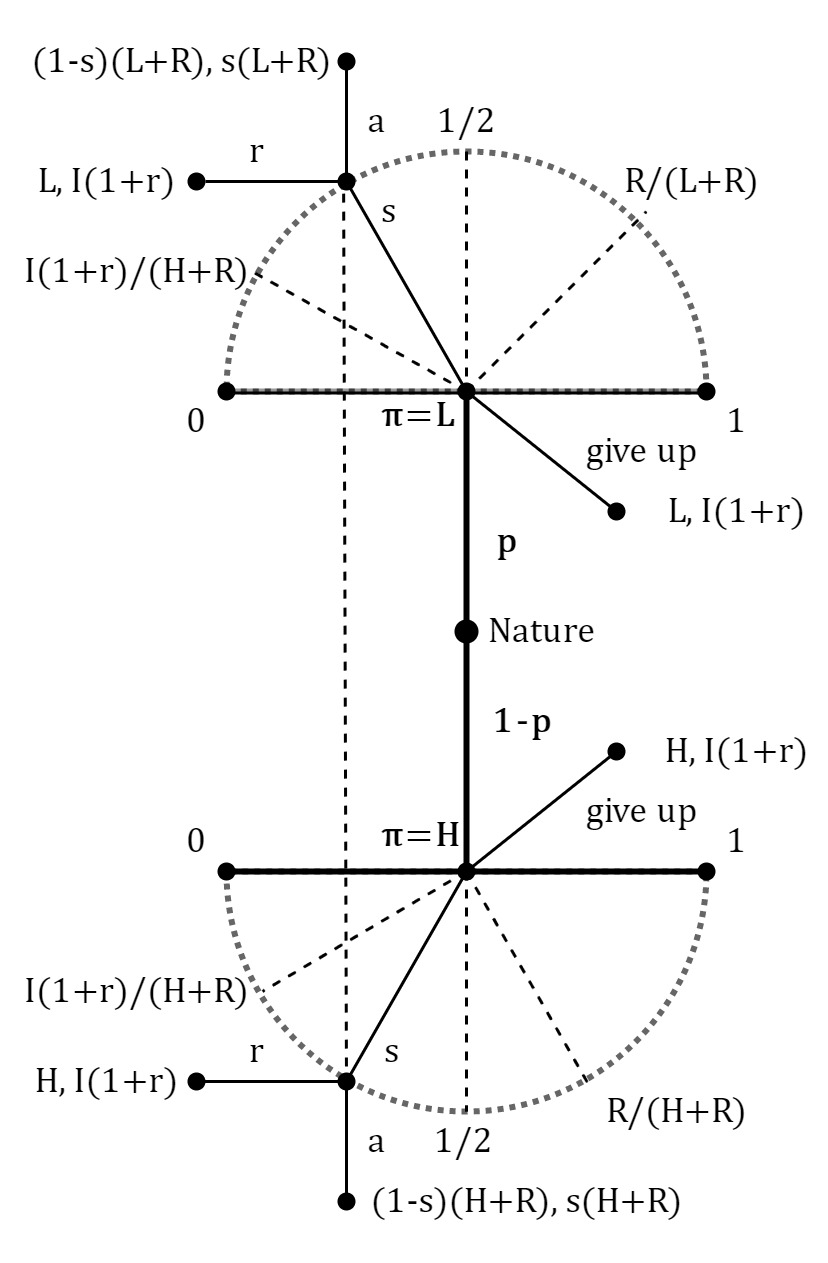
Different types of firms have different profitability, π. It is assumed that p represents the probability that a firm’s profit is low, π = L and that 1-p represents the probability that the firm’s profit is high, π = H, where H > L > 0. To realize an investment opportunity with the payoff R, the firm needs to find an investor who will invest the sum I. Attractiveness of the project is described with the inequality R > I (1 + r), where r represents the investor’s alternative rate of return. To compensate for the needed funds, the firm will offer to the investor an equity stake, s є [0,1], in the aggregate value of the firm after the project’s realization, π+R. The investor can accept or refuse the offer, but, because the game is played under the condition of information asymmetry, he does not have the information about the firm’s profitability. The firm can also decide not to undertake the project. The article will define a perfect Bayesian equilibrium in a signaling game between the firm and the investor. Figure 1 shows the signaling game between the firm and the investor along with the timing and payoffs of the players. Nature plays the first move and determines a type of firm. The firm knows which type has been determined and has the interval of strategies s є [0,1] from which one is designated in Figure 1 along with the corresponding information set. If the firm decides to give up the project, the game ends. The investor has two strategies for each offer received by the firm, accept the offer, a, or refuse, r. Payoffs of the players are indicated at the final nodes of the game, left being the payoff of the firm and right being the payoff of the investor. For the firm it is only rational to offer an equity stake, s, if and only if, (1-s)(π+R)≥π, π+R-s(π+R)≥π, R≥s(π+R), s≤R/(π+R) (1)
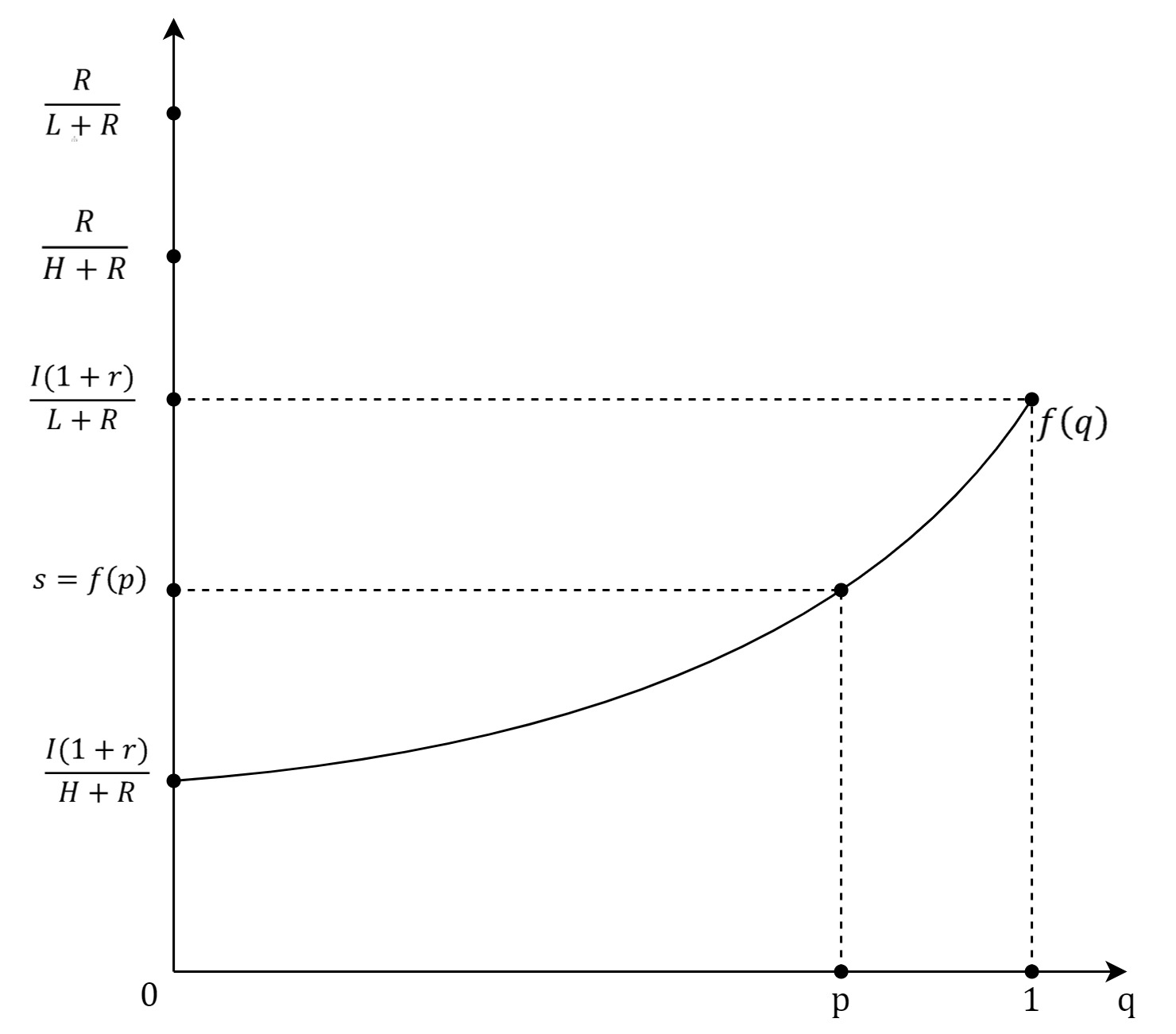
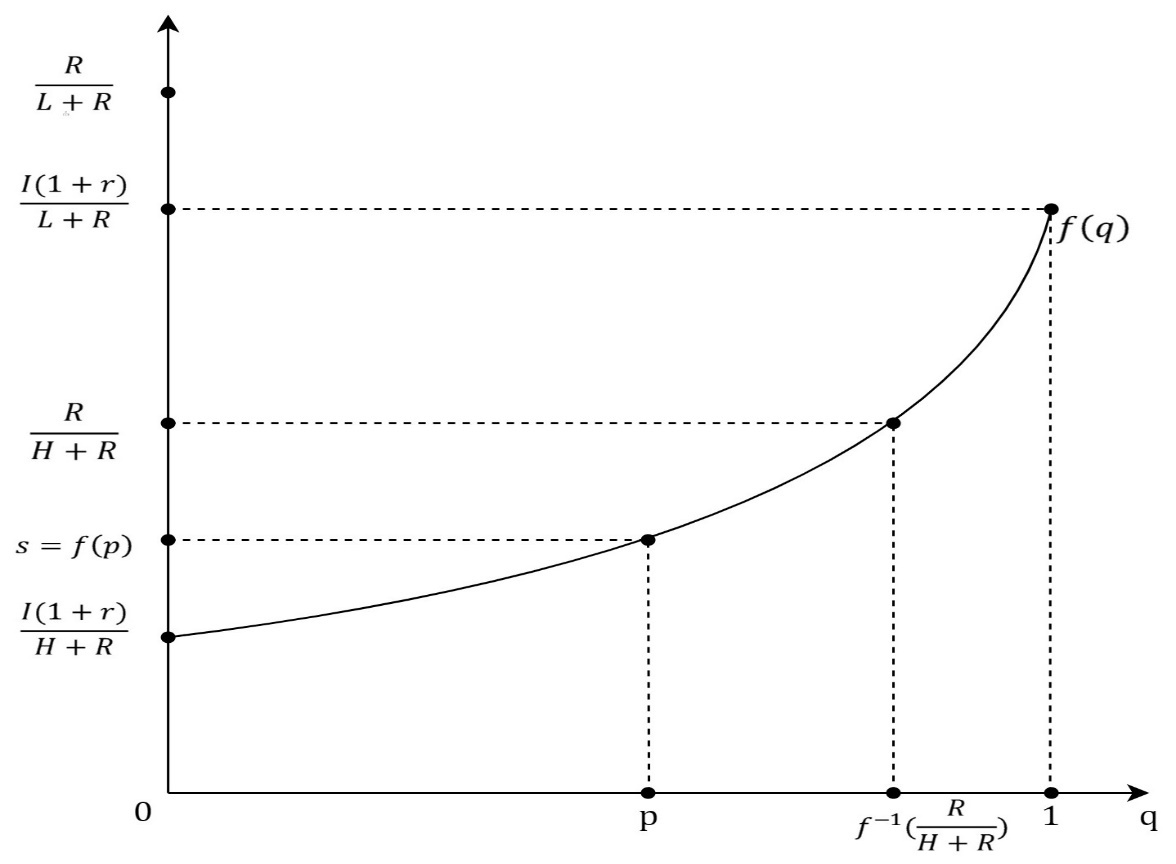
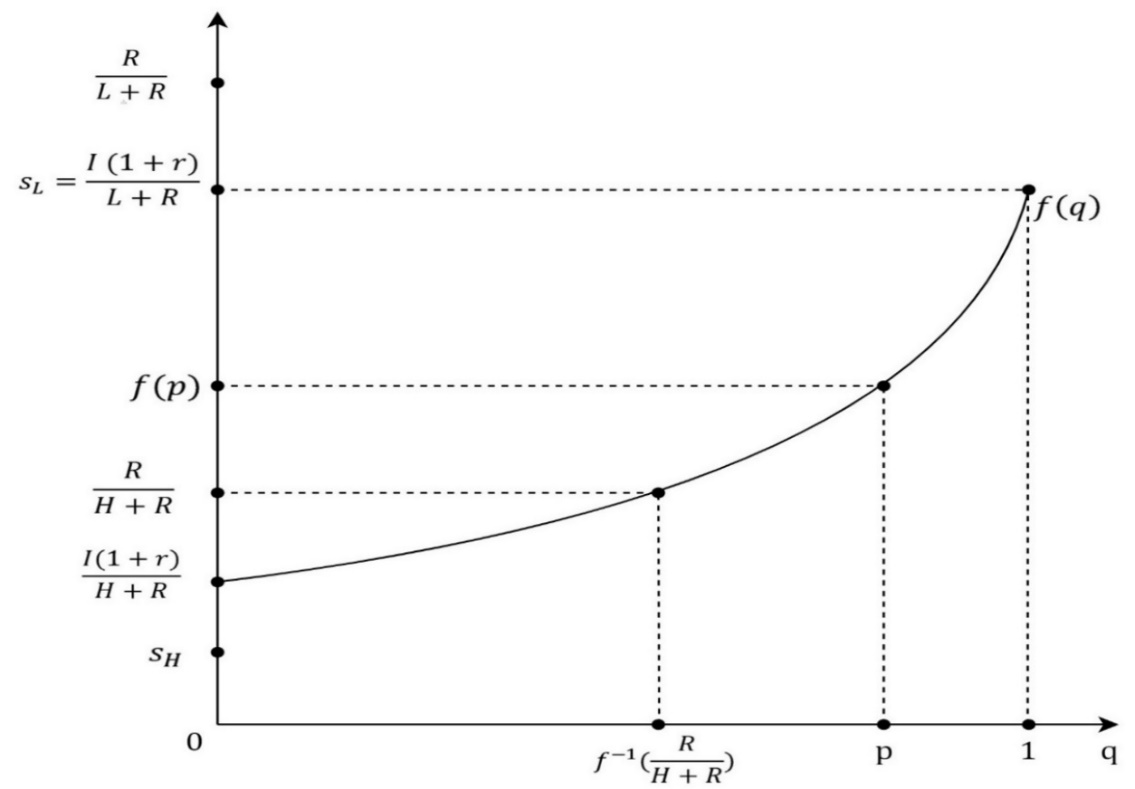
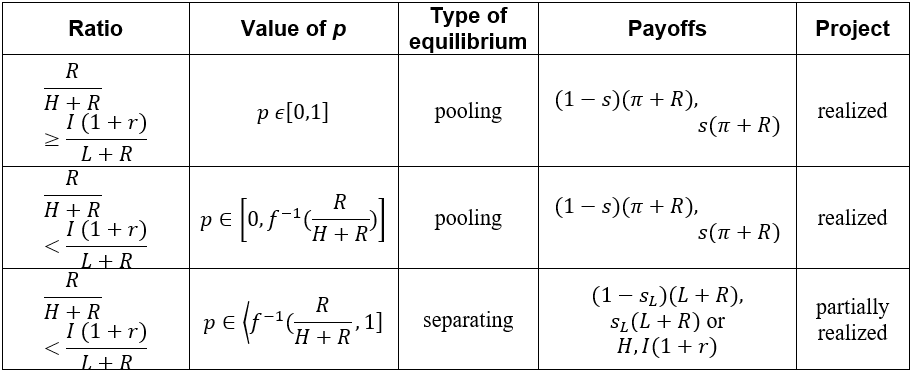
Otherwise, the firm will be at a loss if the investor accepts an equity stake, s, that does not satisfy the equation. In a signaling game, a Receiver, because of the condition of information asymmetry, interpreters a move played by a Sender as a signal which informs him about a type of a Sender. Therefore, a Receiver’s strategy needs to be following a created belief or a probability, about which type could have played the move. For the Receiver’s strategy to be a part of the perfect Bayesian equilibrium, the created belief needs to be determined by the Bayesian formula and a strategy of the Sender. Hence, the investor’s belief is described with q = p, where p stands for the probability by which Nature determines the type of firm or a frequency of the type of firm in a market. If there were no information asymmetry every belief will be equal to 1. For every offer, s, received by the firm, the investor has a belief, q, that the offer is sent by the L-type of the firm. Then, 1-q is the probability that the offer is sent by H-type of the firm and the corresponding payoff of the investor is qs(L+R)+(1-q)s(H+R)=s (2) If the investor rejects the offer, then his payoff is equal to I(1+r). For the investor, it is rational to accept the offer s, if and only if, s[qL+(1-q)H+R]≥I(1+r), s≥I(1+r)/(qL+(1-q)H+R)=f(q). (3) The lowest offer which the investor accepts is s=f(0)=(I(1+r))/(H+R), when he is certain that the H-type offered the equity stake. A graph of the function f(q), shown in Figure 2, will be used for a description of the perfect Bayesian equilibrium. In the perfect Bayesian equilibrium, the firm’s strategy needs to be per the criteria, s≤R/(π+R). The investor’s strategy also needs to be under the criteria, s≥f(q), depending on the created belief, q. The project will be realized only when the firm’s offered equity stake is equal to or bigger than the equity stake the investor would accept, s_F≥s_I. Furthermore, depending on the belief, q, the H-type equity share, s_H=R/(H+R), and the equity share the investor would accept when certain L-typed played the move, s=f(1)=(I (1+r))/(L+R), there can exist a pooling or a separating equilibrium inside the perfect Bayesian equilibrium. In the pooling equilibrium, both types of firms could have played the same move and the signal does not inform the investor about the type of firm. If R/(H+R)≥(I (1+r))/(L+R) then the pooling equilibrium exists for every probability, p, that the firm is L-type. The equilibrium is described with the firm’s offer, s = f (p), which the investor accepts, Figure 2. Lower equity stakes, ones that will be better for the firm, the investor does not accept if his belief is still q = p. If R/(H+R)<(I (1+r))/(L+R) and the investor’s belief that the L-type sent the offer is small enough, p∈[0,f^(-1) (R/(H+R))], then the offer, s = f (p), which the investor accepts is still the description of pooling equilibrium, Figure 3. If R/(H+R)<(I (1+r))/(L+R) and the investor’s belief that the L-type sent the offer is big enough, p∈⟨f^(-1) (R/(H+R)┤),├ 1], then pooling equilibrium does not exist, Figure 4. In that case, exists separating equilibrium in which the L-type offers equity stake, s_L=(I(1+r))/(L+R) which the investor accepts and the H-type offers equity stake, s_H<(I(1+r))/(L+R) , which the investor rejects. Offers s ϵ 〈R/(H+R),s_L 〉 are not rational for the H-type of the firm so the investor’s belief is described with q = 1 and he will reject them. Offers s≤R/(H+R) the investor also rejects the belief described with q = p. Offer s_L which the investor accepts for the H-type is not rational and the result is the perfect Bayesian equilibrium. It is important to notice that if R/(H+R)>(I (1+r))/(L+R), for H-type it is better to offer s_L then s_H and then separating equilibrium does not exist.In the separating equilibrium, for the described values of the ration and the value of p, the project gets realized for both types of firms. However, in the pooling equilibrium, the project gets realized only for the L-type of the firm. In that case, the payoff for the L-type will be (1-s_L )(L+R),s_L (L+R), and the payoff for the H-type will be H,I(1+r). Even though the game is not modeled in that manner, it is noticeable, when R/(H+R)≤s=f(p) holds, that the H-type would have an interest in signaling the investor about the type, in other words, for H-type it would be beneficiary to lower the belief, p, that the firm is L-type because that would mean the realization of the project and the better welfare.
THE MODEL WITH 3 TYPES OF FIRMS
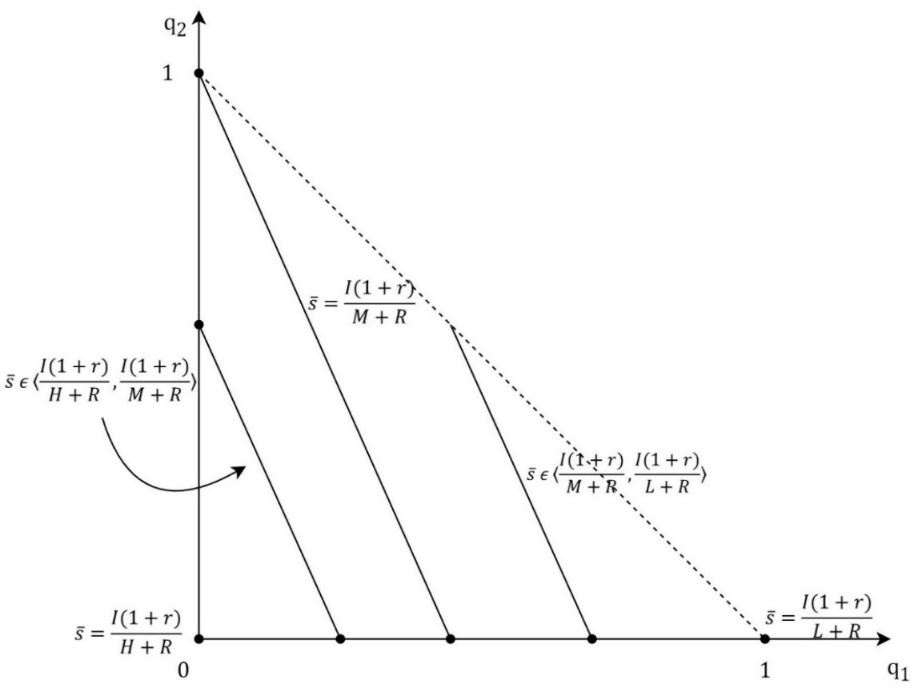
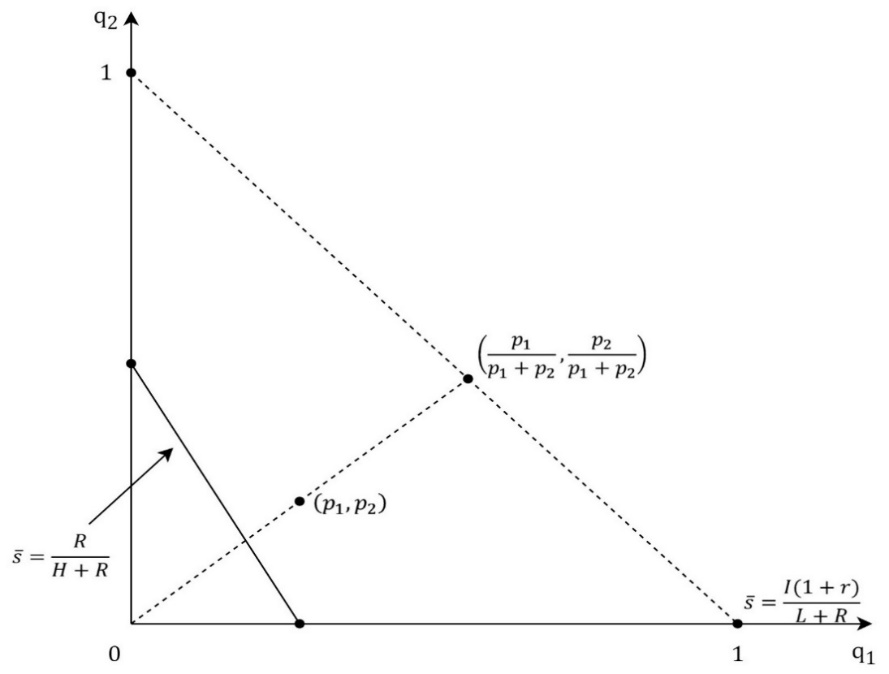
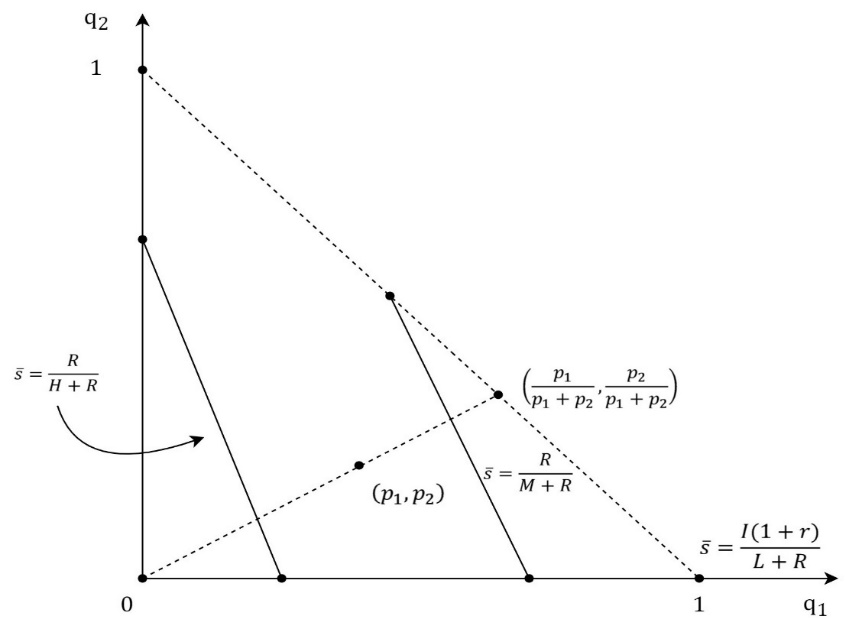
The previous analysis can be expended by adding the M-type of a firm whose profit is π = M, where H>M >L>0. Therefore, a probability that a firm is the L-type is p_1, a probability that a firm is the M-type is p_2, and a probability that a firm is the H-type is 1-p_1-p_2. The signaling game between a firm and an investor in the model of 3 types of a firm has the same structure as the model of 2 types of a firm. The investor’s belief that an offer comes from the L-type, the M-type, or the H-type is described with probabilities q_1, q_2 and 1-〖q_1- q〗_2. If the investor accepts the offer his payoff is q_1 s(L+R)+q_2 s(M+R)+(1-q_1-q_2 )s(H+R)=s[q_1 L+q_2 M+(1-q_1-q_2 )H+R] (4) Otherwise, the investor’s payoff is I(1+r). For the investor, it is rational to accept the offer if and only if s[q_1 L+q_2 M+(1-q_1-q_2 )H+R]≥I(1+r), s≥I(1+r)/(q_1 L+q_2 M+(1-q_1-q_2 )H+R)=g(q_1,q_2 ). (5) The graph of function g(q_1,q_2 ) is shown in Figure 5. The function g(q_1,q_2 )=(I(1+r))/(H+R-q_1 (H-L)-q_2 (H-M)) is strongly increasing and the following inequalities hold g(0,0)=(I(1+r))/(H+R)<g(0,1)=(I(1+r))/(M+R)<g(1,0)=(I(1+r))/(L+R). (6) The equation of the level line of the function g(q_1,q_2 ) is g(q_1,q_2 )=s ̅, (I(1+r))/(H+R-q_1 (H-L)-q_2 (H-M))=s ̅, H+R-q_1 (H-L)-q_2 (H-M)=(I(1+r))/s ̅ , q_1 (H-L)-q_2 (H-M)=H+R-I(1+r)/s ̅ (7) Interval of s ̅ is [(I(1+r))/(H+R),(I(1+r))/(L+R)] and for boundary values level sets are points. Figure 6 shows the level line for the function g(q_1,q_2 ). The absolute value of the slope of the level curve is (H-L)/(H-M) and it is bigger than 1. The following cases should be observed: 1.) case: If R/(H+R)≥(I (1+r))/(L+R) then the firms offer, s=g(p_1,p_2 ), is the description of the pooling equilibrium where the investor’s belief is described with q=(q_1,q_2 )=(p_1,p_2 ) and the investor accepts the offer. Lower offers, the ones that will be better for the firm, the investor will not accept if his belief does not change. The pooling equilibrium then exists for every probability distribution of the firm’s types. 2.) case: If R/(H+R)<(I (1+r))/(L+R) and g(p_1,p_2 )≤R/(H+R) then the firms offer, s=g(p_1,p_2 ), which the investor accepts, is still the description of the pooling equilibrium. 3.) case: If R/(H+R)<(I (1+r))/(L+R) and g(p_1,p_2 )>R/(H+R) then the pooling equilibrium does not exist.
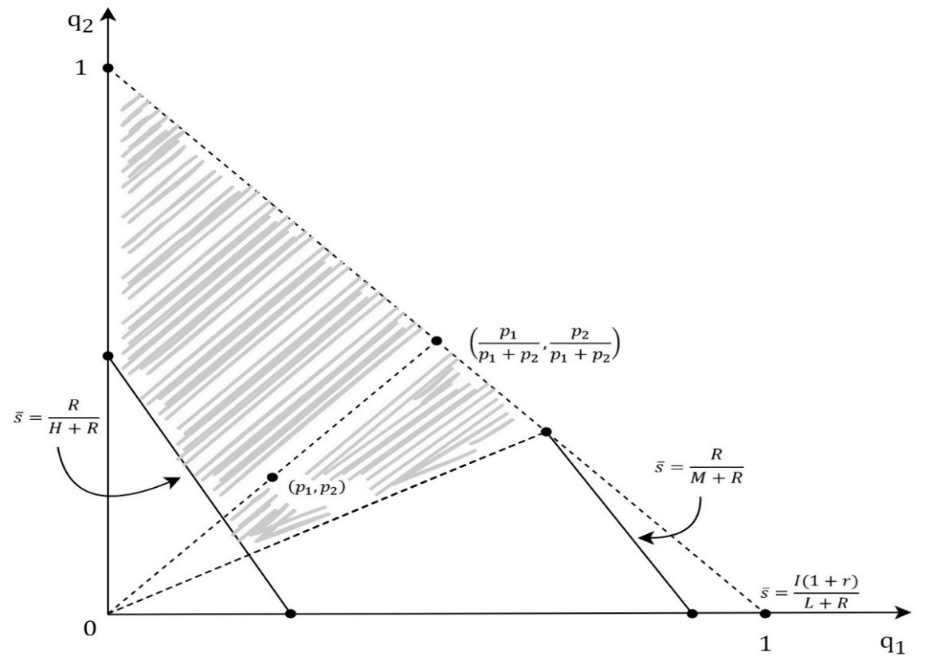
The next subcases should be observed: 3.a) subcase: If R/(H+R)≥(I (1+r))/(L+R) then in the perfect Bayesian equilibrium, the H-type of the firm offers the equity stake, s_H<(I(1+r))/(H+R), which the investor rejects. The next two types offer the same equity stake, s=g(p_1/(p_1+p_2 ),p_2/(p_1+p_2 )) which the investor accepts because his belief is determined by the Bayesian formula and the firm’s strategy, Figure 7. For equity stake offers, which are not included in the firm’s strategy, the investor’s belief is determined by the Bayesian formula and the principle that lower shares could only be offered by the type of the firm for whom it is rational to offer the lower share. Therefore, for the offers, s ϵ〈R/(H+R),g(p_1/(p_1+p_2 ),p_2/(p_1+p_2 ))〉, which would put the L-type and the M-type in the better position, the investor’s belief is described with q=(p_1/(p_1+p_2 ),p_2/(p_1+p_2 )), and he rejects the offers. The equity stake offers, s<R/(H+R), the investor also rejects because then his belief is q=(p_1,p_2) and g(q)=g(p_1,p_2 )>R/(H+R)≥s. It is also important to notice that for the H-type there is no rational offer which the investor would accept. 3.b) subcase: If R/(M+R)<(I (1+r))/(L+R) and g(p_1/(p_1+p_2 ),p_2/(p_1+p_2 ))≤R/(M+R) then still the H-type offer,s_H<(I(1+r))/(H+R), which the investor rejects, and the L-type and the M-type offer, s=g(p_1/(p_1+p_2 ),p_2/(p_1+p_2 )), which the investor accepts, are the description of the perfect Bayesian equilibrium, Figure 8. The perfect Bayesian equilibrium exists for the probabilities which are described within the shaded are excluding the level line when s ̅=R/(H+R). 3.c) subcase: If R/(M+R)<(I (1+r))/(L+R) and g(p_1/(p_1+p_2 ),p_2/(p_1+p_2 ))>R/(M+R), then equity stake offers, s_H<(I(1+r))/(H+R), s_M<(I(1+r))/(M+R) and s_L=(I(1+r))/(L+R), are the description of the perfect Bayesian equilibrium, where the investor accepts only the offer from the L-type, s_L. If s_H≠s_M, then the game has got the separating equilibrium, Figure 9. If s∈〈R/(M+R),s_L 〉, then the investor’s belief is q=(1,0), g(q)=(I(1+r))/(L+R)=s_L>s and the investor rejects the offer. If s∈⟨R/(H+R),├ R/(M+R)]∖┤ {s_H,s_M } then the investor’s belief is q=(p_1/(p_1+p_2 ),p_2/(p_1+p_2 )), g(q)=g(p_1/(p_1+p_2 ),p_2/(p_1+p_2 ))>R/(M+R)≥s and the investor rejects the offer. If s≤R/(H+R) and s∉{s_H,s_M } then the investor’s belief is q=(p_1,p_2 ),g(q)=g(p_1,p_2 )>R/(H+R)≥s and the investor rejects the offer, which is in accordance with the perfect Bayesian equilibrium.CONCLUSION
Firms that do not have enough funds to take advantage of a valuable investment opportunity, need to find an investor, whose funds can secure the realization of the project. Both, a firm and an investor, need to decide under the condition of information asymmetry because the investor does not know the firm’s profitability. The relationship is modeled as a signaling game and this article is revising Gibbon’s model with two types of firms along with the analysis of the derived result. The article is precisely defining which small enough probabilities of the L-type of a firm will cause the existence of the pooling equilibrium. Also, the article defines which big enough probabilities of the L-type of a firm will cause the existence of the separating equilibrium. The conditions are stated under which a separating or a pooling equilibrium does not exist. The revision of Gibbon’s results is complemented with the graphical representation of the game, which is showing the timing and the payoffs of the game. The description of equilibrium is done by defining a function, along with its graph, for the lowest equity stake that would be accepted by the investor who is rational and has created a belief about a firm’s profitability. The signaling model is expended adding one more type of a firm and also is the set of possible equilibriums. The function for the lowest equity stake that would be accepted by the investor who is rational and has created a belief about a firm’s profitability is shown graphicly in a three-dimensional space, along with its properties. The analysis of the level lines of the function enables to differentiate cases and to describe conditions under which there is an existence of a pooling, a semi-pooling, and a separating equilibrium. Analytical description of the conditions complements the graphical description which gives clear visibility of the share of the financially attractive projects which do not get realized. The limitation of the article is that it only analyzes an equity stake offered in exchange for the funds needed for the project’s realization. Future research may include the analysis of more types of firms and different types of contracts, between a firm and an investor, which will reduce the negative economic consequences occurring because of the number of financially attractive projects that do not get realized.