INTRODUCTION
For evaluation of business enterprises, complex multi-parameter econometric models are build up. As it is well known that tiny variations of input data may induce large changes on output, econometric models are employed for the analysis of the sensitivity of an entity to viable internal and external conditions often changing very abruptly. As probing input data combinations is impossible partly due to obvious danger of irreparable damages to the entity, experimenting on the mathematical model is safe and allows for reliable what-if analysis and forecasting. Econometric models are sets of mutually conjugate equations based on time series of economic categories often delayed. Such models consist generally of two elements: time series of econometric categories and set of coefficients relating them. Thus accuracy of coefficients is crucial for reliability of the model. Common methods of evaluation of coefficients are e.g. ARMA (Autoregressive Moving Average), ARIMA (Autoregressive Integrated Moving Average), ARMAX (Auto Regressive Integrated Moving Average with eXogeneous Input) or regression-based methods. Unfortunately, this gives point estimates only while due to imminent inaccuracy of learning datasets they are rather interval estimates. There are generally two attempts to overcome this limitation – Monte Carlo simulations and fuzzy number or interval arithmetic – both have pros and cons. Fuzzy number methods despite intense research and development still suffer problems concerning computation complexity as well as convergence1. However, the solution may be obtained in a single computation pass2. Oppositely Monte Carlo based methods are presently very well explored. However, in order to produce reliable results, they require multiple repetitions of every simulation pass and subsequent statistical analysis. Another problem is the need to use long and uncorrelated series of random numbers, however present day pseudorandom number generators, like Mersenne Twister3, Matsumoto4, allows to overcome this limitation. The direct bonus of this procedure is obtaining empirical probability distribution estimate of output data. Furthermore, due to enormous computation power of contemporary computers, considerable computation complexity of Monte Carlo based methods is no more the problem5. One of the problems of MC based methods is often complex and hard to assess structure and hierarchy of conditional decisions. In the article, hypothesis is verified that Monte Carlo based Characteristic Surface Model is useful for modelling of economic output of a single small touristic entity in the era of pandemic. Alongside numerical efficiency of the Model, ability to recreate typical scenarios will be investigated as well as ability of assessment of risk level and of estimation of fluctuations level. For the case study, Croatian touristic industry was selected due to its specificity including strong influence on the State economy. The Methodology section consists of 6 subsections. In the first specificity of tourism in Croatia is analysed. In the second one, Characteristic Surface Method, extended characteristic surface model (eCSM) is introduced as an efficient tool for determination of stochastic coefficients in econometric models. Accordingly, relevant terminology is explained. In the next section, Design of the Numerical Experiments, experimental setup is presented and explained. In the fourth section, econometric model of hypothetic private, small touristic entity is presented as a base for calculations presented in the next section. Characteristics of layers adopted in this exemplary case is presented in Layers Data subsection. In the last subsection computer program written as test tool for the case study has been described, as well as other software utilized. In the next section, Results, attempt is made to perform numerical modelling of evolution of consumer sentiment using characteristic surface method on the example of tourism industry in the era of SARS-Cov-2 pandemic. In particular, applicability of estimation of influence of input data, (e.g. population structure) on model output values is analysed. Computational results for eight different scenarios are presented; two examples display influence of discounts on final profit of the entity. Next two sections are devoted to discussion of results and presentation of final conclusions.
METHODOLOGY
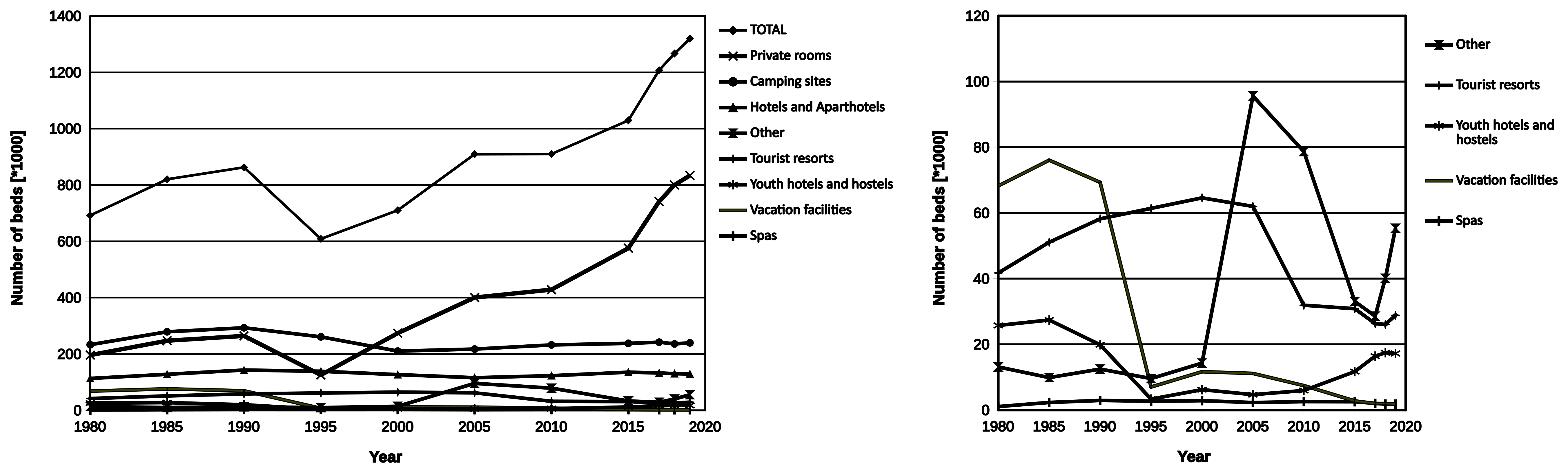
Specificity of Tourism in Croatia For the case study, tourism in Croatia has been chosen due to its remarkable specificity. Economics of Croatia, as well as more than 40 other countries, depends heavily on tourism. According to some authors, share of tourism in overall economy for 2017 was about 19,6 %, which is almost one third of the whole services sector ‒ 70,1 %6,7 compared to industrial output at 26,2 % and agriculture 3,6 %. Other sources give even higher figures up to 25 % in year 2019 and 383 400 jobs (9,3 % of population) involved in the tourism industry8. Different figures may result from taking into account real contribution to Gross Domestic Product (GDP) accounted for 15.2 billion of US$9, while the other may include revenues (13 billion US$ in year 2019) of touristic industry only8. Due to analysis of Orsini and Ostojić10, Croatia has the highest share of tourist revenues in GDP among countries like Cyprus, Greece, Malta, Italy, and Spain. This makes Croatian economy very sensitive to even minor fluctuations. At real GDP PPP accounting $116,34 in 20197 Croatia was 85th country in the world, however taking into account GDP per capita ($28 602) was even higher ‒ 72nd which means substantial progress if compared to year 20177,11. After a collapse initiated in 2008 by world financial crisis Croatia started recovery in late 2014 which culminated in 2019 at GDP growth rate at 2,9 %, declining public debt (to 73,2 % of GDP) (The World Bank12) and notable reduction of unemployment rate to below 7 % from 15 % in 2015 (7). It was speculated that due to SARS-Cov-2 outbreak, GDP may shrink by more than 8,1 %. Unemployment rate was estimated at 7,5 % in 2020 Q311 while previous estimates were even higher at 9 %. While governmental emergency package (Croatia Week13) may help reducing the economy downturn, it was forecasted, that it would increase budget deficit and substantial rise of public debt even up to 84 % GDP by the end of 2020. Moreover, a fiscal deficit may set a record rising close to 7 % of GDP. It was expected that economy would rebound in the second half of 2020 (The World Bank,12) but no conclusive figures are available yet. It is expected that pre-epidemic levels may be reached no sooner than in 202214. Decline in number of overnights in 2020 was not distributed evenly. For example, Rab island, claimed as “Covid free zone” noticed only minor decrease of number of tourists15. This stresses up role of FUD (fear, uncertainty and doubt) in planning or abandoning holiday travel plans. Characteristics of tourism in Croatia changed abruptly in 1995. Up to 1995 the shares of domestic and foreign tourists were comparable, however thereafter share of domestic tourists remained on war time level, while number of foreign tourists rapidly rebounded to a record number of 21 million in 2019 (5 % increase vs. 201816-18). This has changed in 2020, as in March only drop of 75 % in number of tourists was recorded year to year19. Figures for the April were even more severe reaching 99,8 % drop19. However preliminary data showed that in a whole year reduction of overnights was lesser than expected, at 54,0 million versus 91,24 million in year 2019 (59,2 %)18,20. Accommodation structure is one of the most interesting factors of Croatian tourists industry17,18. While number of beds in hotels and camping sites barely grows or even decreases, number of beds in private accommodation entities more than tripled compared to year 1995 (Figure 1). Not only does it make Croatian tourism unique, but also has important social and economic consequences e.g., by helping reducing jobless rate (very high among youth, 17,8 % in 201921) as many facilities are operated by families. Another fast-growing tourism sector is nautical tourism18; p.33, which stayed unexpectedly strong amid epidemic in year 202022. This may be attributed to adventurous nature of sailors. Structure of private accommodation in Croatia is moderately diversified. Based on data from rental agencies, offered entities range from small, one or two apartments (rooms or studios) facilities up to luxury micro hotels for say ten families. What makes them distinct from regular hotels is management ‒ private accommodation is by rule governed by a single family or even one person only. Average number of overnights per arrival depends on the month. In the summer, it approximates to six days/one week (July, August), 5 days in June and September and less than three days in the rest of the year. This is probably caused by policy of owners of private accommodations and camps who restrict reservations to the whole week in high season and lift that limitation in other months17,18. Furthermore, number of overnights vary during the year and peaks in July/August far more than in other countries10. Strong seasonality is another weakness of tourist industry.
Average number of overnights per arrival depends on country of origin too. While tourists from Germany, Czech Republic and Poland arrive to Croatia for one week on average (7,2, 6,8 and 6,5 respectively), the ones from Austria, Slovenia, Hungary, UK and Italy stay for approximately 5 days18. Visits from other countries are shorter than four days. According to governmental data in 2020 only number of overnights generated by tourists from Poland was substantially higher than in 201923, peaking at 12,4 % of all bed nights a bit less than Slovenes tourists (13,5 %) but ahead of Czechs (9,2 %) and Austrians (6 %) while Germans retained first place with 33,3 % of all overnight stays24. What is intriguing is that the choice of accommodation type strongly depends on the country of origin. It may be best presented as dependency of proportion of number of overnights in private accommodation and the number of overnights in hotels, on the country of origin – P/H. Based on data from y.201918, four different groups may be spotted (Figure 2). The first one contains only one country – Poland (P/H = 7,67). The second group consists of Czech Republic, Hungary, Germany, Italy and Slovenia (2,1 < P/H > 5,42). To the third one belongs France and “other countries” (1,5 < P/H > 1,7). The last one consists of USA, Austria and UK (P/H < 1.0). While sentiment of Polish tourists toward private accommodation may be attributed to more affordable prices or just preferred form of vacationing, the difference between Austria and Germany is more difficult to understand. Both countries are comparably wealthy and are in similar distance from Croatia with Austria being obviously nearer. This puzzle should be explained in separate research. There is one more thing to note, namely rapid grow of P/H factor for some countries like Poland or Czech Republic with stagnation for others like Slovenia, UK or USA (Figure 2, right). P/H factor lesser than one, spotted for travellers from USA, Canada or UK may be attributed to luggage limitations imposed by airlines. This makes hotels the first choice for accommodation. However, this does not explain low value of P/H factor for Austria i.e. 0,9 (0,7 in 2018), as Croatia is easily accessible by car and there are no serious luggage limitations. Larger figures for private accommodation may result also from that increase of number of hotel beds requires more investments, thus owners of private accommodations tune to market requirements faster. Analysis of available offers suggests that typical price per week/per arrival ranges from 400 up to 600 €, however prices over 1000 € per week are not uncommon. It should be stressed that as the euro is widely accepted (and often expected) in all payments (services, restaurants, tolls and goods) it became the second currency of Croatia, even prior to official access to Eurozone, expected as soon as in year 2022 as Croatia currently participates in the ERM II since July 10th 202025.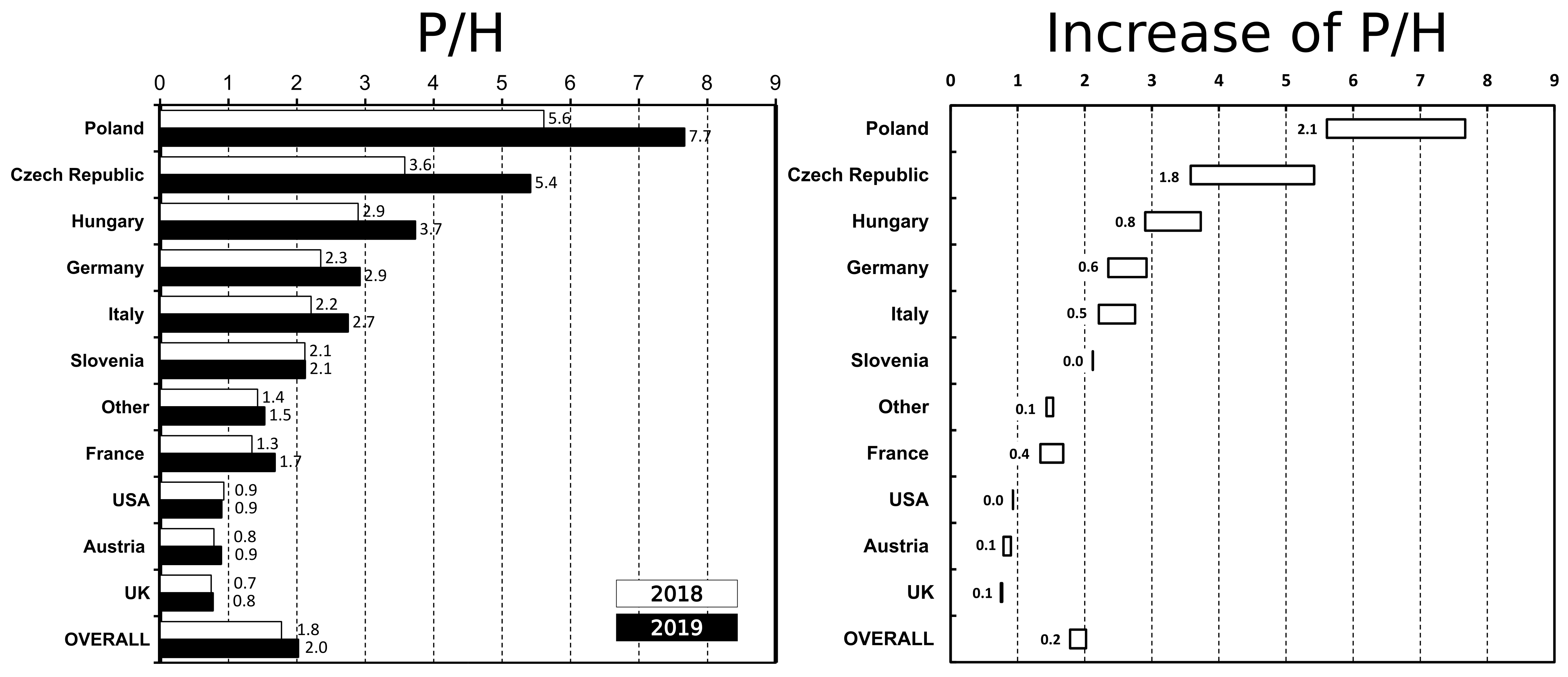
*all values are estimated or assumed and varied depending on test Layers data Identification of layers is the key point of the model. While sentiments are usually inert, in response to intense signals (e.g. disasters like epidemic or earthquake) they may change rapidly. For example recovery of frozen economy, thereafter lockdown will take some time due to aversion to the risk especially present in the tourist industry. Obviously, there is no rest in the presence of risk (excluding people adherent to risk). Identification of layers and their sensitivity to variety of signals is complex task, requiring not only access to raw data but trained experts and specialized software too. Luckily, this does not need to be done frequently as once computed layers do not change rapidly or change in the predictable manner.
In order to study a numerical experiment three layers have been assumed in the try to model recovery from the lockdown. As layers are shaped according to bivariate correlated Gaussian distribution (1), they are fully defined by 6 parameters: standard deviations (σ1 and σ2), means (μ1 and μ2), correlation coefficient (ρ) i.e. components of covariance matrix, and share in the population (S). All values are presented in the Table 2. Probability density function f(x) of bivariate correlated Gaussian distribution is defined by the formula:
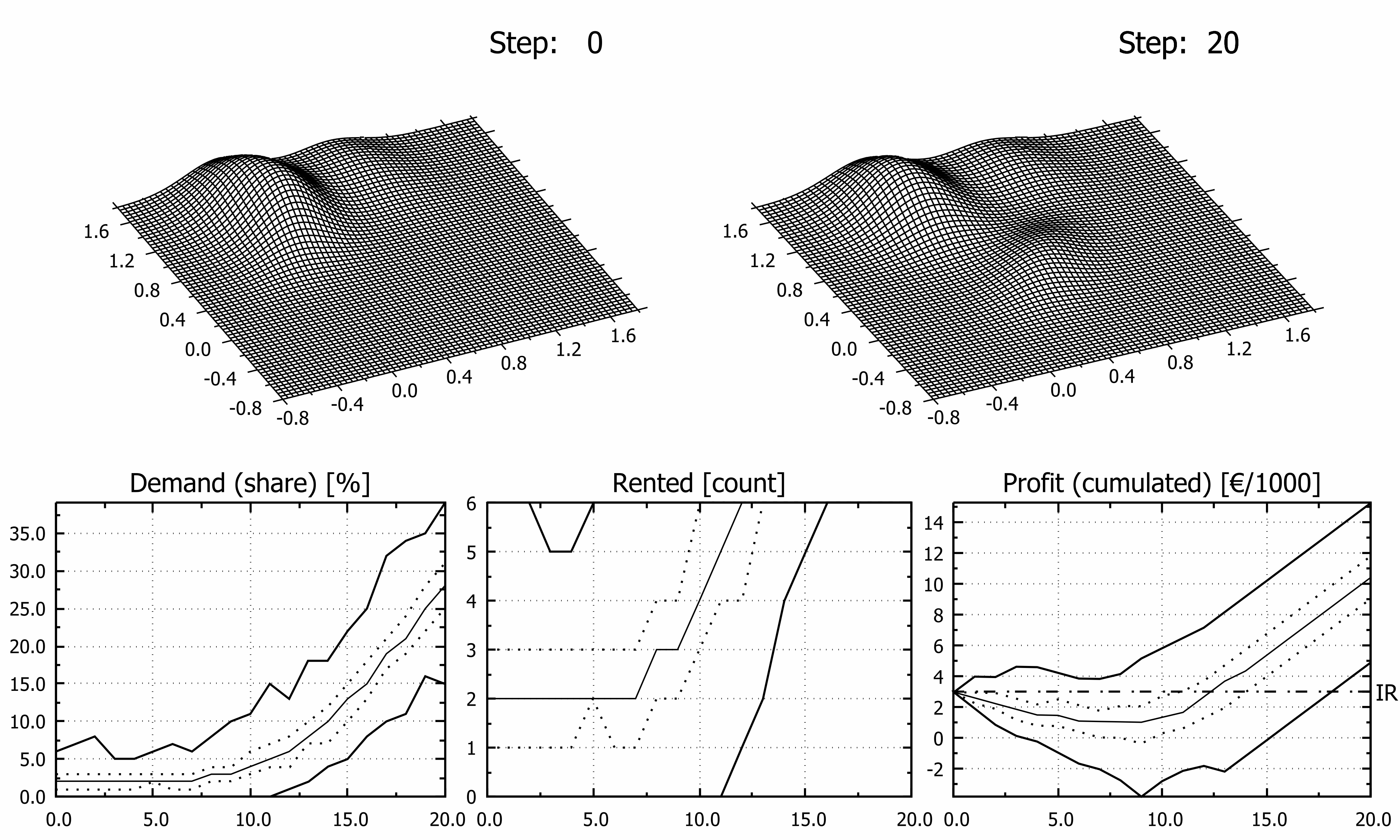
where x represents 2D point coordinates, µ denotes the mean (2D point as well) and C -1 is inverse of related covariance matrix. For higher dimensions formula stays the same excluding normalizing factor which depends on the dimensionality. In all scenarios Layer L3 migrates steadily from the selected initial state to the final state (ref. Table. 2). Uniform displacement per time step was hereby implemented nevertheless it may be step dependent. Layer L3A describes sentiments during normal season while layer L3B describes sentiments in the middle of first epidemic wave. The other layers have been assumed static in order to reduce number of variables in numerical experiments. However, in fully developed model they should “migrate” too and relative share of layers would probably change as well. Although variable, time dependent or stochastic displacement of the surface may be easily applied, it is out of scope and goal of this article as it introduces many new factors irrelevant to current discussion. It may be assumed that L1 and L2 layers represent domestic tourists not very favoring modelled destination, and less prone to foreign travel ban. Resulting Characteristic Surface may be symbolically denoted as CS = S1∙L1 + S2∙L2 + S3∙L3(t). Computer Program and Other Software Used Model has been implemented as C language console program (GCC compiler, tdm-1, v.5.1.0), source code is available for research groups on demand. According to the algorithm used, computing time scales linearly with the size of the population sample ‘N’ and number of repetitions ‘K’, thus BigO is of rank N×K. Use of regular laptop was sufficient for all calculations. Typical time of the single simulation was approximately 0,1 seconds over 20 week period (computed using clock() function), it was tested that 100 repetitions were optimal for convergence while not affecting significantly computing time. Charts have been prepared using gnuplot 5.4.135 and tuned using Inkscape 1.0236, if required. Obtained results are presented mainly on multi image (hybrid) charts. Images are arranged in two rows. Top row presents shape of Characteristic Surface before and thereafter migration of the monitored surface while a lower row shows estimated share of demand of monitored entity, number of apartments rented and cumulated profit respectively. In all charts lines presents minimum/maximum (solid bold line), lower and upper quartile (dotted line) and median (solid line) of depicted category. Vertical scales are expressed as percentage “Demand (share)” chart, as count of items in “Rented” chart and in thousands of euro (“Profit (cumulated)” chart). On the “Profit” chart black dashed horizontal line at y = 3, labelled ‘IR’ on secondary ‘Y’ axis depicts initial financial resources.RESULTS
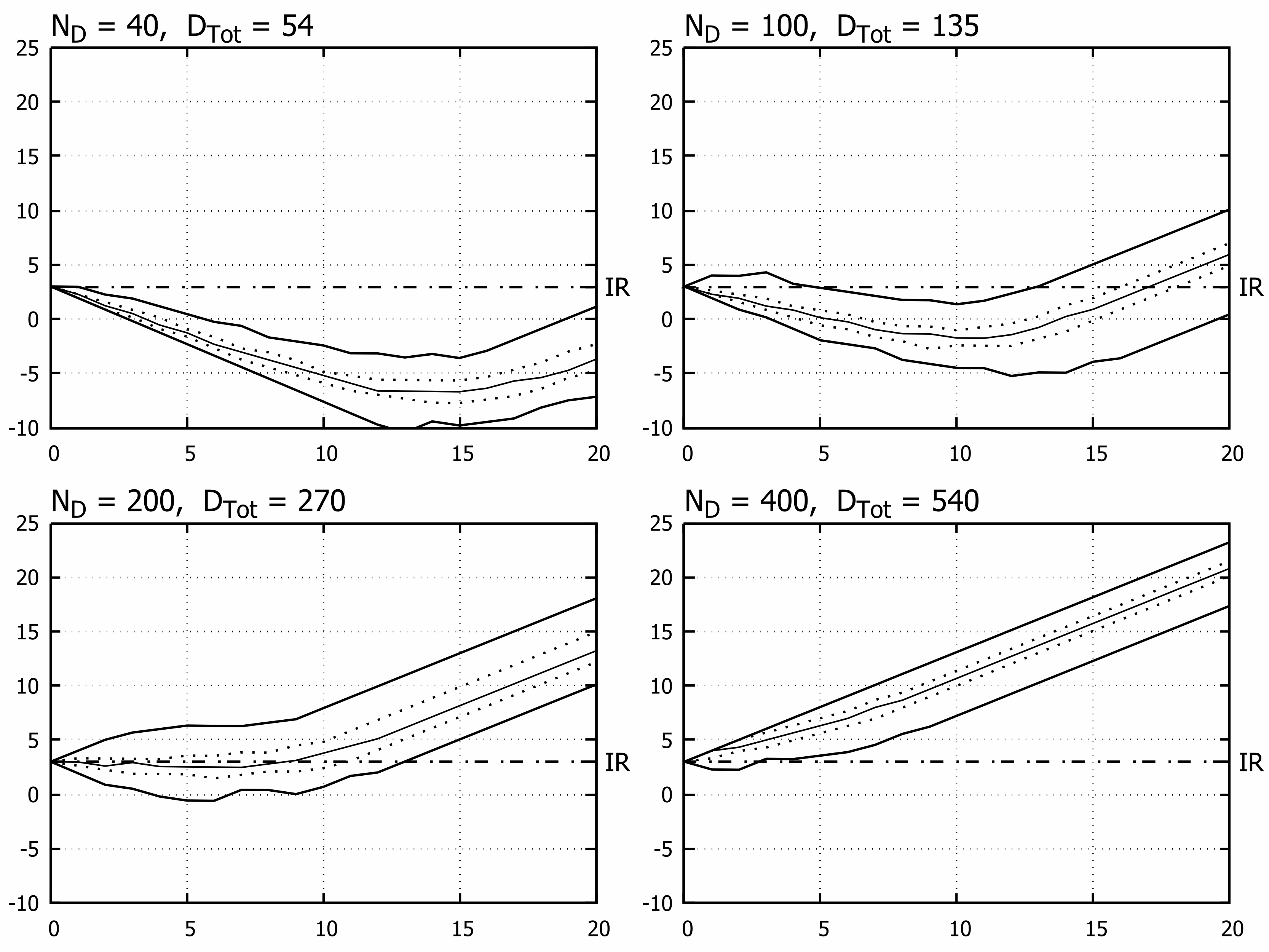
From a plenty of possible and tested scenarios seven were selected for the presentation of the model (Figures 3 to 9). Migration of the third layer from epidemic L3B state toward one of states L3A, L3C or L3D was assumed in all investigated cases but first two. Four more experiments were done in order to reveal influence of scale effect on estimated profit (Fig.10). Basic values of attributes of the model are presented in the Table 1. Maximum theoretical cumulated profit after whole season was 27 400€ (all apartments rented all the time) while the highest possible loss 21 200€ (no guests at all). In Figure 3 results of simulation assuming undisturbed season are presented, i.e. parameters of all disputed layers are constant over time. Specifically, this means that L3B layer was identical to L3A layer i.e. characteristic surface was the same in the course of simulation so it is drawn once in that Figure.

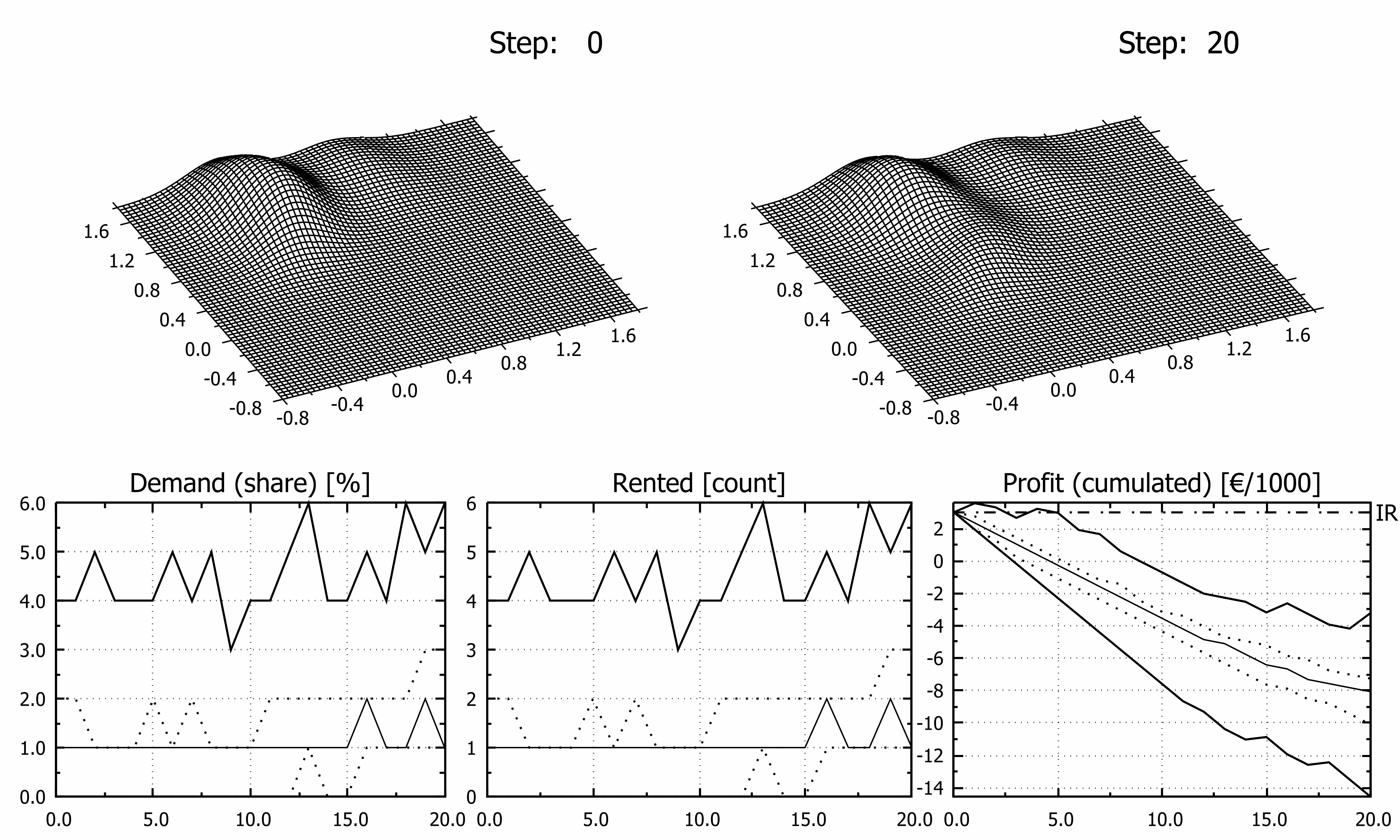
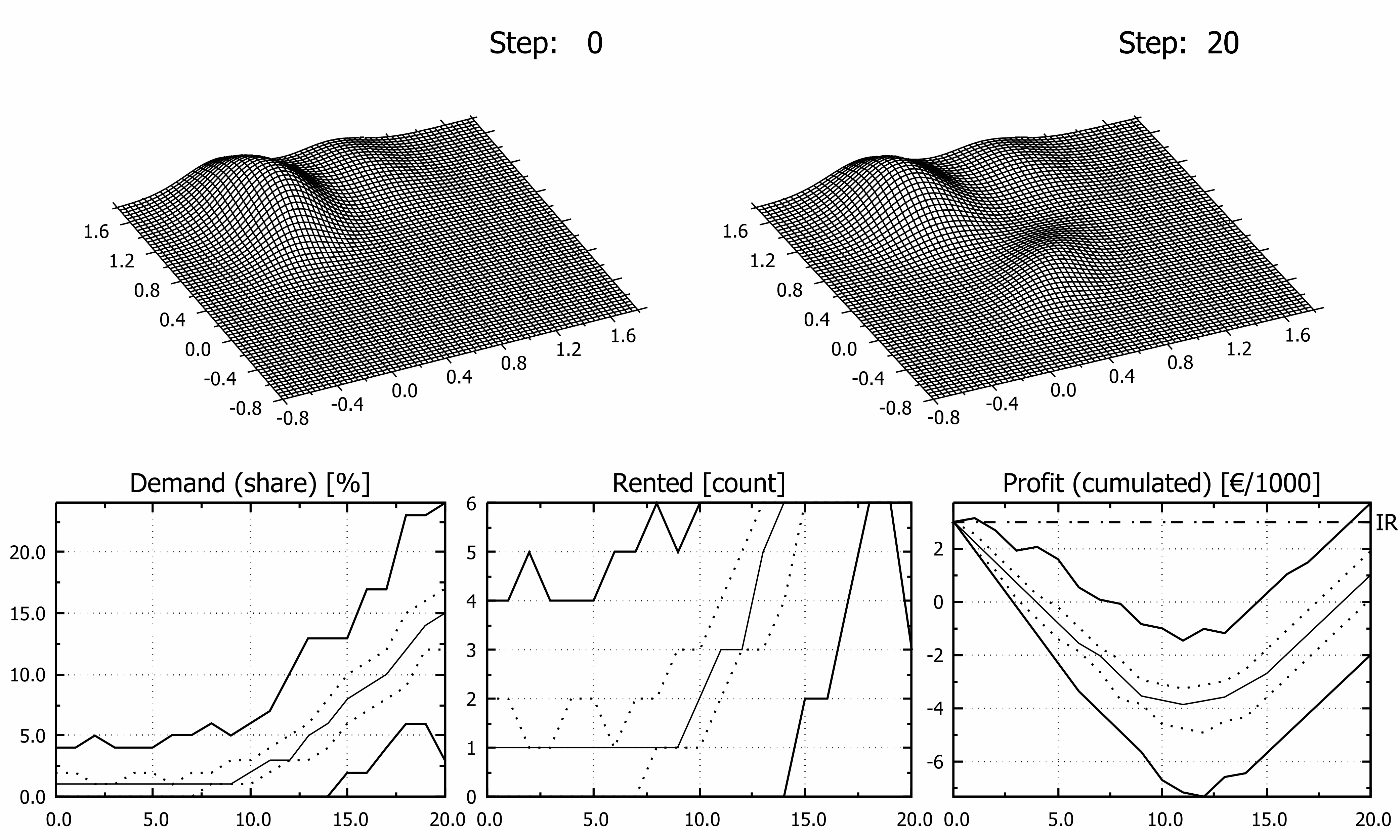
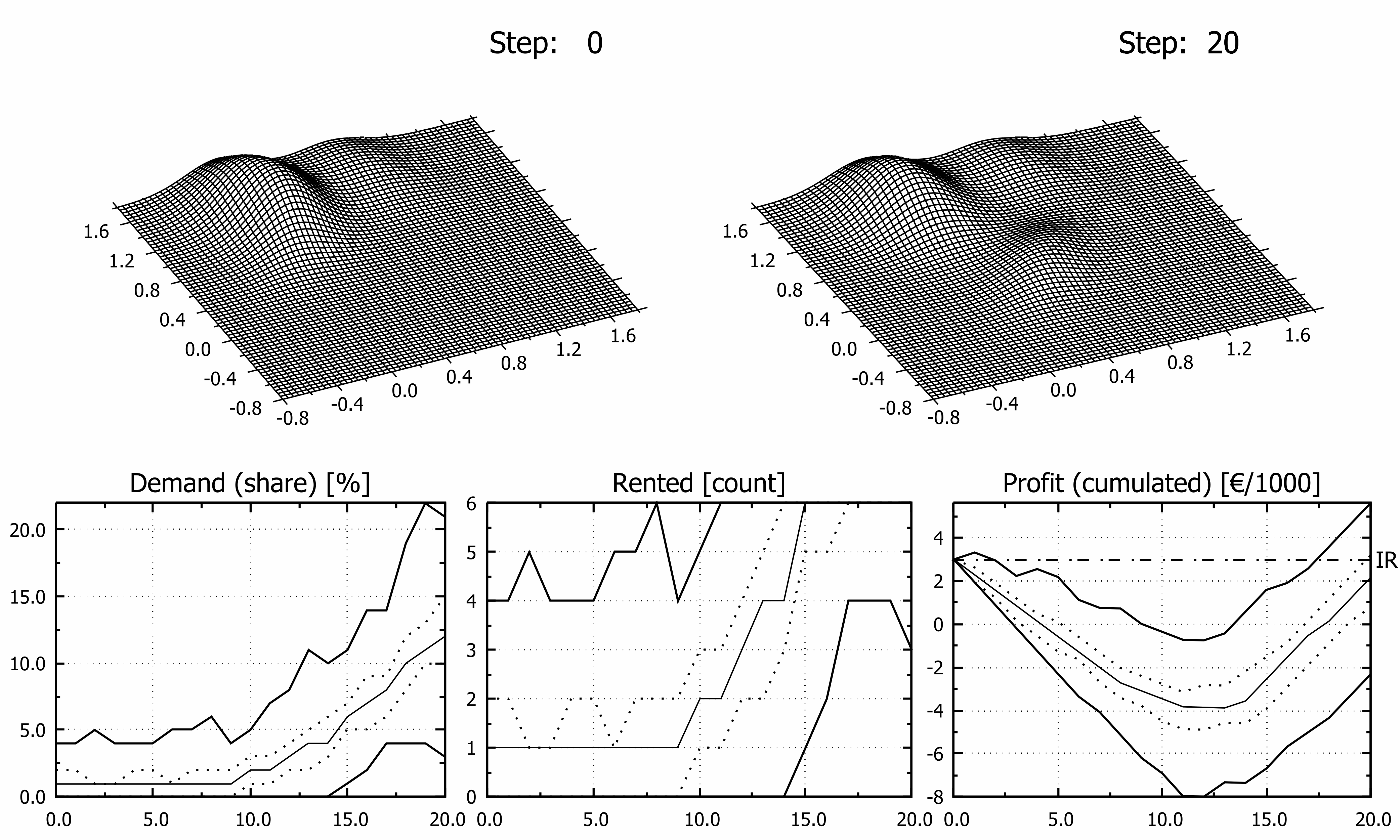
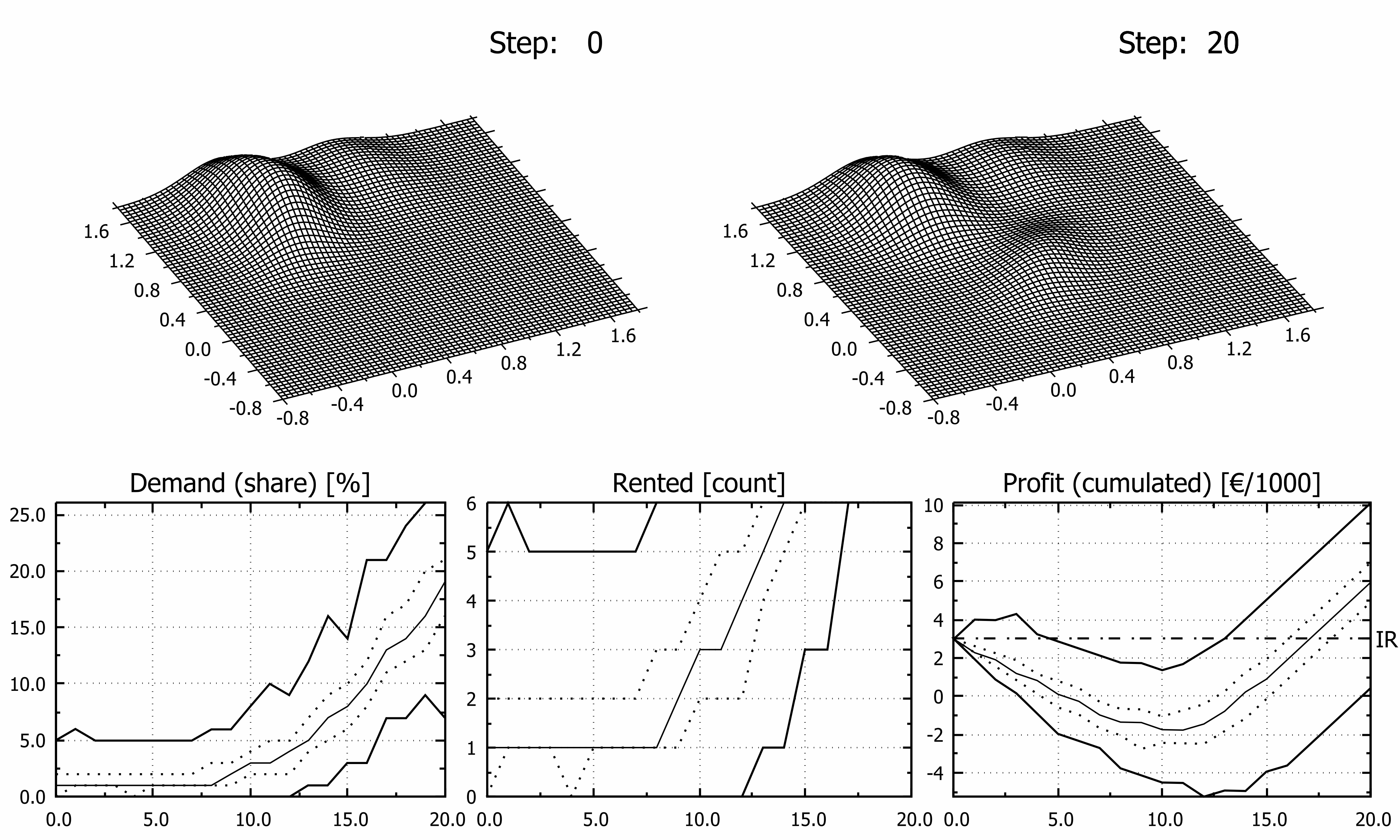
DISCUSSION
Results presented in the previous section suggest that Characteristic Surface model is useful for modelling of economic output of a single small touristic entity in the era of pandemic. As the Model is founded on very weak assumptions, it is very general as well, and may be easily adopted to a variety of scenarios. Numerical efficiency of the Model is satisfactory and the Model itself scales linearly with number of repetitions and size of population involved. However, referential implementation of the Model may still be optimized by parallelization of computations for larger samples. According to results presented above, the Model exhibits ability to recreate typical business scenarios. The Model is sensitive to even small variations of the input data in all tested scenarios. Every parameter of the Model may be treated as a specific “degree of freedom” of its own variability range. Even after restricting number of options to M = 2, number of layers to L = 3 and omitting parameters of econometric model, number of possible combinations (Cartesian product) of remaining parameters: data of Layers (6×L, float numbers), population size N (positive integer), criterion function definitions (numerable, infinite), transfer function definitions (numerable, greater or equal 1) is infinite. For the selected case study on forecasting of recovery of Croatian tourism industry from epidemic, a few conclusions can be made. As increasing rate of rented apartments is crucial for cumulated profit, it may be assessed in a different manner. One possibility is that high social skills of the host, commonly addressed as emotional intelligence, may help increase attractiveness of a given entity over competitors. In terms of Characteristic Surface Model, this may be expressed as an additional push from social skills on layer L3 toward higher competitiveness (bigger µ1 values). Enhancement of the offer is possible as well. Markus et al.37 suggest that introduction of additional items like sports activities to the offer, may help increase sales. Applying discounts may increase the number of rented apartments but may deteriorate profit, thus it must be precisely computed. Surely, small revenues are always better than no revenues, however discounts must be calculated in order to maximize incomes. On the country level, there are more options available. In the first place, I would mention reducing stress and fear of potential guests, as there is no holidays in the presence of critical risk. This may be obtained by several means including (but not limited to) additional, low cost health assurance, increase of number of events for tourists – festivals, concerts or charming fisherman’s evenings, improving operation of highways toll system which currently is highly inefficient, safer organization of travelers resting places & fuel stations and strong support for domestic tourism. Of course, these remedies must be introduced by governmental agencies. Hypothesis may be formulated that post epidemic tourists are more adventurous then others and expect active offers, like nautical tourism, biking, climbing. This might be verified in dedicated research. As shown in the Results section, the Model allows for risk assessment for selected scenario. Furthermore, according to properties of MonteCarlo method, range of variability for computed outputs may be estimated.
CONCLUSIONS
Presented hereby method seems to be useful for the what-if analysis, giving quantitative answers thus allowing for decision making at known risk. While using of the model is rather simple, fine-tuning of crucial parts of the model might not be easy and may require a lot of additional research including variety of methods from simple A/B testing up to the most complex AI/ML. In particular, layers for the specific population may be subject of scientific research on its own. Results may be published by governmental agencies ready for use by individual entrepreneurs. Furthermore, besides new computational method, model introduces own descriptive language suitable for discussion concerning behaviour of analysed population. As assumptions the Model is built upon are very weak, it has almost no limitations. The main problems are proper identification and attribution of layers, determination of the response patterns (i.e. evolution of CS due to signals and time) and adoption of proper criterion function. Model easily scales with population size and may be applied to small, medium and large-scale systems. Although shown on the example of tourist industry, presented Model is universal and may be implemented for a variety of scenarios, including forecasting of general elections, demand on selected goods or number of visitors in National Park at a variety of weather conditions. Due to universal basics of the model another possible fields of implementation are sciences like physics or engineering. Possible areas of further development include methods of determination of Characteristic Surface, introduction of innovative transfer functions and development of time dependent criterion functions, including past experience simulation.