License (open-access, http://creativecommons.org/licenses/by-sa/4.0/):
CC-BY-SA
License (open-access):
Prava korištenja: CC-BY-SA
License (open-access):
Journal content is published under CC-BY-SA licence.
Publication date: 2020
Volume: 19
Issue: 33
Recenzija, prikaz
Mjerenje duljina i površina u Google Mapsu i Google Earthu
Nedjeljko Frančula
Google je 2005. godine pokrenuo na internetu Google Maps, uslugu namijenjenu snalaženju u prostoru i kretanju od jedne točke do druge automobilom, javnim prijevozom, pješice, biciklom ili zrakoplovom. Pritom je u izradi matematičke osnove karata primijenio postupak u kojem su geodetske koordinate na elipsoidu φ i λ preslikane u ravninu po formulama uspravne Mercatorove projekcije za preslikavanje sfere.
Google Maps; Google Earth; Mercatorova projekcija
243433
30.6.2020.
Posjeta: 2.615 *
Distance Calculator (2020) Distance Calculator – How far is it?.https://www.timeanddate.com/worldclock/distance.html ( 23.04.2020. )
Frančula N (2019) A New Mathematical Basis of Google Maps / Nova matematička osnova Google Mapsa. Kartografija i geoinformacije, 18, 31, 109-114. https://doi.org/https://doi.org/10.32909/kghttps://hrcak.srce.hr/222074 ( 23.04.2020. )
Frančula N, Tutić D, Lapaine M, Viličić M (2019) Google Earth and Map Projections / Google Earth i kartografske projekcije. Kartografija i geoinformacije, 18, 32, 192-199. https://doi.org/https://doi.org/10.32909/kghttps://hrcak.srce.hr/236159 ( 23.04.2020. )
Kupier J A, Ayers A J, Holm M E, Nowak M J (2014) Python Coding of Geospatial Processing in Web-based Mapping Applications. In Proceedings of the 13th Python in Science Conference, edited by S. van der Walt, and J. Bergstra, 41-47.http://conference.scipy.org/proceedings/scipy2014 ( 23.04.2020. )
Lapaine M, Frančula N, Vučetić N (1993) Površina hrvatskog mora i otoka. CAD Forum 1993, Zbornik radova, CAD sekcija Saveza društava arhitekata Hrvatske, Zagreb 47-52.https://www.bib.irb.hr/296039 ( 23.04.2020. )
MathWorks (2020) areaint – Surface area of polygon on sphere or ellipsoid.https://www.mathworks.com/help/map/ref/areaint.html ( 23.04.2020. )
PROJ 7.0.0 (2020) Geodesic calculation.https://proj.org/geodesic.html ( 23.04.2020. )
Skopeliti A, Stamou L (2019) Online Map Services: Contemporary Cartography or a New Cartographic Culture?. ISPRS International Journal of Geo-Information, 8, (5) 215, 1-28. https://doi.org/https://doi.org/10.3390/ijgi8050215https://www.mdpi.com/2220-9964/8/5/215 ( 23.04.2020. )
Wikipedia (2020a) Greenland.https://en.wikipedia.org/wiki/Greenland ( 23.04.2020. )
Wikipedia (2020b) Africa.https://en.wikipedia.org/wiki/Africa ( 23.04.2020. )
Wikipedia (2020c) Australia.https://en.wikipedia.org/wiki/Australia ( 23.04.2020. )
Wikipedia (2020d) Geodesics on an ellipsoid.https://en.wikipedia.org/wiki/Geodesics_on_an_ellipsoid ( 23.04.2020. )
Zinn (2010) Web Mercator: Non-Conformal, Non-Mercator.http://www.hydrometronics.com/downloads/Web%20Mercator%20-%20Non-Conformal,%20Non-Mercator%20(notes).pdf ( 23.04.2020. )
In 2005, Google Maps was launched on the internet as a service intended to aid orientation in space and navigation from one point to another by car, public transport, on foot, by bicycle, or by plane. In making the mathematical basis of the maps, Google Maps applied a procedure in which geodetic coordinates on the ellipsoid φ and λ were mapped into a plane according to the formulas of the normal Mercator projection for mapping a sphere. This approach can be interpreted as a double projection of the ellipsoid into a plane. First, the ellipsoid is mapped to a sphere, whereby the geographic coordinates on the sphere are the same as the geodetic coordinates on the ellipsoid. Next, the sphere is mapped into a plane using the Mercator normal projection formulas (Frančula 2019). The main reason why Google adopted this approach for the production of Google Maps was that the formulas for mapping the sphere are much simpler, and therefore five times quicker to calculate, than the formulas for mapping the ellipsoid (Zinn 2010). This approach produces a new map projection close to Mercator’s, with the important difference that it is not conformal, like the Mercator projection, but approximately conformal, since the maximum distortion of the angles is not greater than approximately 23 arc minutes (Zinn 2010). It is known as the Web Mercator projection. Since mid-2018, Google Maps has also been available in a new mathematical base (accessed by clicking ‘Globe’ on the menu). Most of the maps in the new mathematical base are in the Web Mercator projection, though the smallest-scale maps are not maps of the world, but maps of the hemisphere in an azimuthal projection (Frančula 2019).
In 2005, Google also launched Google Earth. This is a virtual globe, that is, a three-dimensional (3D) software depiction of the Earth on the screen of a computer or smartphone. The general perspective projection was implemented for the cartographic depiction (Frančula et al. 2019). We assume that the same approach as in Google Maps was used also in Google Earth, that is, geodetic coordinates from the ellipsoid were included in the general perspective projection formulas for mapping the sphere.
Accordingly, maps in both Google Maps and Google Earth were acquired by mapping the ellipsoid, not the sphere, onto a plane. This must be emphasised, since Google Maps and Google Earth both have tools for measuring lengths and areas. When using these tools, lengths and areas will be the dimensions they are on the ellipsoid, free of the influence of projection distortions.
Many authors are not aware of this and claim the opposite is true. For example,Kupier et al. (2014) claim that the maps in the Web Mercator projection, which forms the mathematical base of Google Maps, “should not be used for … computing lengths or areas because of the distortion inherent in the projection”. They compare the results of measuring areas in the USA on Google Maps and on a map produced in the Albers conical equivalent projection, in which the differences are about 40%.Skopeliti and Stamou (2019) claim, “On the contrary, although a distance measure tool is provided in Wikimapia and Google Maps, distance measurements do not always correspond to true distances, due to great deformations away from the Equator”.
We will demonstrate that measurement of lengths and areas in Google Maps is free from the influence of projection distortions by measuring the shortest distance, that is, the length of geodesic line, between Madrid and Moscow, and the area of Greenland on maps in the Web Mercator projection.
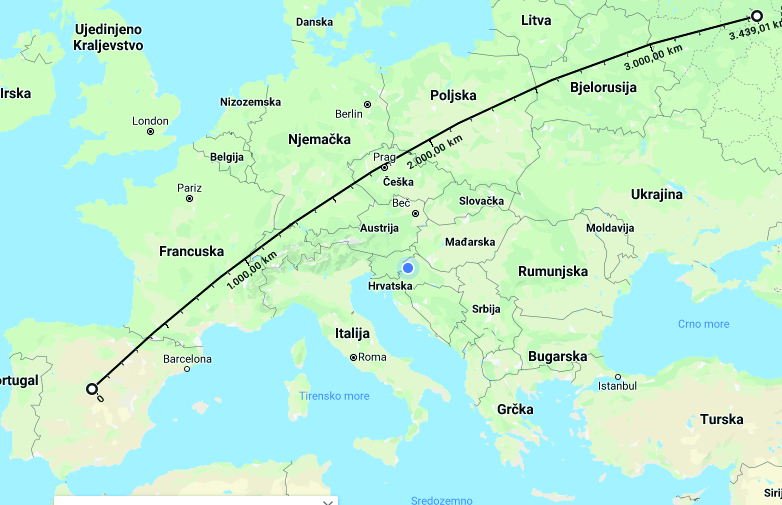
To measure the distance from Madrid to Moscow, we right-clicked on Madrid and selected ‘Measure the distance’, then clicked on Moscow (Figure 1). The result was 3,439 km. According toDistance Calculator (2020), the distance is 3,448 km. Obviously, the result using Google Maps was free from projection distortion.
To measure the area of Greenland, we right-clicked on a starting-point and selected ‘Measure the distance’. We traced the coastline of Greenland roughly and finished back at the starting-point. A pop-up box then shows the length of the coastline to be 8,021 km and the area 2,146,522 km2 (Figure 2). According toWikipedia 2020a, the area of Greenland is 2,166,086 km2, so obviously that by measuring the area on Google Maps, the area on the ellipsoid was obtained, thus free of the projection distortion. We should mention that on the Web Mercator projection, Greenland is only a little smaller than Africa, although it is actually about 14 times smaller. According toWikipedia 2020b, Africa has a area of 30,370,000 km2.
To measure lengths and areas in Google Earth, we selected ‘Show ruler’ on the toolbar. In the box that appears we selected ‘Lines’ and kilometres as the unit. We measured the distance between Kuala Lumpur and Jakarta by clicking on Kuala Lumpur and then on Jakarta. The result was 1,178 km (Figure 3). According toDistance Calculator (2020), the distance is 1,175 km.
We will present another proof that measuring in Google Earth produces the dimensions on the ellipsoid. We measured the length of the equatorial arc on the map of the hemisphere between the meridians λ = –30o i λ = 30o and the length of the meridian arc between the parallels φ = 30o i φ = –30o. The result for the length of the arc at the equator was 6,673 km (exact length is 6,679 km), while for the length of the arc on the meridian it was 6,649 km (exact length is 6,640 km). Due to the flattening of the Earth at the poles, the length of the arc at the equator is greater than at the meridian. The measurement error regarding the length of the arc at the equator was only 0.09%, and at the meridian it was 0.13%.
To measure area, we selected ‘Polygon’, for the unit of ‘Perimeter’, kilometres, and for the unit of ‘Area’, square kilometres. The result for the length of the coastline of Australia was 13,938 km, and the area was 7,599,812 km2. According toWikipedia 2020c, the area of Australia is 7,692,024 km2. Since we were using a small-scale map and only traced the coastline of Australia roughly, and since the area we measured only differed from the exact one by 1.33%, we concluded that our measurement corresponded to the area on the ellipsoid.
How were the distances and areas in the above examples calculated? If you right-click anywhere in Google Maps and select What’s in here? a pop-up box shows the name of the object and its geodetic coordinates down to six decimal points (Figure 5) or in degrees of minutes and seconds down to tenths of seconds.
In Google Earth, on the lower part of the screen the geodetic coordinates which correspond to the current position of the cursor on the screen are shown. The coordinates are given in degrees, minutes and seconds, with a rate of precision of hundredths of seconds (Figure 6).
It is logical to assume that the lengths and areas in Google Maps and Google Earth are calculated on the ellipsoid, since the geodetic coordinates for all points are known. In the literature, formulas for calculating the length of geodesic lines and the areas of polygons on the ellipsoid have been provided (Wikipedia 2020d). There are also algorithms and software for calculating the lengths of geodesic lines on the ellipsoid (PROJ 7.0.0 2020) and the areas of polygons on the ellipsoid (MathWorks 2020).
The fact that distances and areas are measured on the ellipsoid does not mean that map projections have been avoided. They are essential for all displays on the computer screen. Only when the display on the screen is in a particular map projection it is possible to click on an individual point and from the projection coordinates and use of inverse cartographic equations calculate geographic or geodetic coordinates.
Finally, it should be noted that lenghts and areas can be determined by measuring on maps in any projection, if one takes into account the distortions of the projection. As far back as 1993, the size of a certain area of the Croatian sea and islands was determined from a 1:1,000,000 scale map in the Gauss-Krüger conformal projection (Lapaine et al. 1993).
Google je 2005. godine pokrenuo na internetu Google Maps, uslugu namijenjenu snalaženju u prostoru i kretanju od jedne točke do druge automobilom, javnim prijevozom, pješice, biciklom ili zrakoplovom. Pritom je u izradi matematičke osnove karata primijenio postupak u kojem su geodetske koordinate na elipsoidu φ i λ preslikane u ravninu po formulama uspravne Mercatorove projekcije za preslikavanje sfere. Taj se postupak može interpretirati kao dvostruka projekcija elipsoida u ravninu. Prvo je elipsoid preslikan na sferu uz uvjet da su geografske koordinate na sferi jednake geodetskim koordinatama na elipsoidu. Potom je sfera preslikana na ravninu po formulama uspravne Mercatorove projekcije (Frančula 2019). Glavni razlog Googleove primjene takvog postupka u izradi Google Mapsa jednostavnije su formule za preslikavanje sfere te stoga i pet puta brže računanje nego po formulama za preslikavanje elipsoida (Zinn 2010). Opisanim postupkom preslikavanja dobivena je nova kartografska projekcija bliska Mercatorovoj s bitnom razlikom da nije konformna poput Mercatorove projekcije, već približno konformna jer maksimalne deformacije kutova nisu veće od približno 23 lučne minute (Zinn 2010). Projekcija je poznata pod imenom web-Mercatorova projekcija. Od sredine 2018. karte Google Mapsa dostupne su i u novoj matematičkoj osnovi (treba kliknuti Globe u izborniku). Većina karata i u novoj matematičkoj osnovi je u web-Mercatorovoj projekciji, ali karta najsitnijeg mjerila nije karta svijeta već karta hemisfere u azimutnoj projekciji (Frančula 2019).
Google je 2005. pokrenuo i Google Earth. To je virtualni globus, tj. trodimenzionalni (3D) softverski prikaz Zemlje na ekranu računalnog monitora ili pametnog telefona. Za kartografske prikaze primijenjena je opća perspektivna projekcija (Frančula i dr 2019). Naša je pretpostavka da je Google u Google Earthu, primijenio isti postupak kao i u Google Mapsu, tj. u formule opće perspektivne projekcije za preslikavanje sfere uvrstio geodetske koordinate s elipsoida.
Prema tome karte i Google Mapsa i Google Eartha dobivene su preslikavanjem u ravninu elipsoida, a ne sfere. To je važno naglasiti jer Google Maps i Google Earth imaju alate za mjerenje duljina i površina. Mjereći tim alatima, duljine i površine bit će veličine na elipsoidu, dakle oslobođene utjecaja deformacija projekcije.
Mnogi autori toga nisu svjesni i tvrde suprotno. Npr.Kupier i dr. (2014) tvrde da karte u web-Mercatorovoj projekciji, koja čini matematičku osnovu Google Mapsa, ne bi trebalo upotrebljavati za računanje duljina i površina zbog velikih deformacija projekcije (Web Mercator projection should not be used for generating buffers or computing lengths or areas because of the distortion inherent in the projection). Uspoređuju rezultate mjerenja površina na području SAD-a na Google Mapsu i karti izrađenoj u Albersovoj konusnoj ekvivalentnoj projekciji pri čemu su razlike u površinama oko 40 %.Skopeliti i Stamou (2019) tvrde da alat za mjerenje duljina u Google Mapsu ne daje točne rezultate zbog velikih deformacija koje nastaju udaljavanjem od ekvatora (On the contrary, although a distance measure tool is provided in Wikimapia and Google maps, distance measurements do not always correspond to true distances, due to great deformations away from the Equator).
Da su mjerenja duljina i površina na kartama u Google Mapsu oslobođena utjecaja deformacija projekcije, pokazat ćemo na primjeru mjerenja najkraće udaljenosti, tj. duljine geodetske linije, između Madrida i Moskve i površine Grenlanda na kartama u web-Mercatorovoj projekciji.
Za mjerenje udaljenosti Madrid – Moskva kliknemo desnom tipkom miša na Madrid i izaberemo Izmjeri udaljenost i potom kliknemo na Moskva (slika 1). Dobivena duljina je 3439 km. PremaDistance Calculatoru (2020) duljina je 3448 km. Očito da smo i mjerenjem na Google Mapsu dobili duljinu oslobođenu deformacija projekcije.
Za mjerenje površine Grenlanda kliknemo desnom tipkom miša na početnu točku i izaberemo Izmjeri udaljenost. Približno smo pratili obalnu liniju Grenlanda i završili na početnoj točki. Tada se u posebnom okviru ispiše ukupna duljina obalne linije 8021 km i površina 2 146 522 km2 (slika 2). PremaWikipediji 2020a površina Grenlanda je 2 166 086 km2 pa je očito da je mjerenjem površine na Google Mapsu dobivena površina na elipsoidu, dakle oslobođena deformacija projekcije. Spomenimo da je na karti u web-Mercatorovoj projekciji Grenland po veličini samo nešto manji od Afrike iako je od nje oko 14 puta manji. PremaWikipediji 2020b Afrika ima površinu od 30 370 000 km2.
Za mjerenje duljina i površina u Google Earthu biramo Prikaži ravnalo na traci s alatima. U okviru koji se pojavi biramo Linija i za jedinice kilometre. Izmjerit ćemo duljinu između Kuala Lumpura i Džakarte klikom na Kuala Lumpur i potom na Džakartu. Dobivena je duljina od 1178 km (slika 3). PremaDistance Calculatoru (2020) ta je duljina 1175 km.
Da se mjerenjem duljina na kartama Google Eartha dobivaju veličine na elipsoidu, pružit ćemo još jedan dokaz. Izmjerit ćemo na karti hemisfere duljinu luka ekvatora između meridijana s dužinama λ = –30o i λ = 30o i duljinu luka meridijana između paralela sa širinama φ = 30o i φ = –30o. Za duljinu luka na ekvatoru mjerenjem smo dobili 6673 km (točna duljina 6679 km), a za duljinu luka na meridijanu 6649 km (točna duljina 6640 km). Zbog spljoštenosti Zemlje na plovima, duljina luka na ekvatoru dulja je od one na meridijanu. Pogreška mjerenja duljine luka na ekvatoru je samo 0,09%, a na meridijanu 0,13%.
Za mjerenje površine biramo Poligon, za jedinicu Perimetra tj. opsega kilometre i za jedinicu Područja, tj. površine kvadratne kilometre. Za duljinu obalne linije Australije dobiveno je 13 938 km, a za površinu 7 599 812 km2. PremaWikipediji 2020c površina Australije je 7 692 024 km2. S obzirom na to da smo mjerili na karti sitnog mjerila i samo približno obilazili obalnu liniju Australije i da se izmjerena površina razlikuje od točne za samo 1,33%, možemo zaključiti da smo mjerenjem dobili površinu na elipsoidu.
Postavlja se pitanje kako su izračunane duljine i površine u prethodnim primjerima. Klikne li se u Google Mapsu desnom tipkom miša na bilo koju točku i izabere Što je ovdje? u posebnom okviru ispisuje se ime objekta i geodetske koordinate u stupnjevima sa šest decimala (slika 5) ili u stupnjevima minutama i sekundama s preciznošću od desetinke sekunde.
Na Google Earthu u donjem dijelu ekrana stalno su vidljive geodetske koordinate koje odgovaraju trenutnom položaju kursora na ekranu. Koordinate su ispisane u stupnjevima, minutama i sekundama s preciznošću od stotinke sekunde (slika 6).
Logično je pretpostaviti da se duljine i površine u Google Mapsu i Google Earthu računaju na elipsoidu jer su za sve točke poznate geodetske koordinate. U literaturi su objavljene formule za računanje duljine geodetske linije i površine poligona na elipsoidu (Wikipedia 2020d). Postoje i algoritmi i softver za računanje duljina geodetskih linija na elipsoidu (PROJ 7.0.0 2020) i površina poligona na elipsoidu (MathWorks 2020).
To što se duljine i površine računaju na elipsoidu ne znači da su kartografske projekcije izbjegnute. One su neizbježne za sve prikaze na ekranu računala. Jedino kada je prikaz na ekranu u određenoj kartografskoj projekciji, moguće je klikom na pojedinu točku iz projekcijskih koordinata inverznim kartografskim jednadžbama izračunati geografske ili geodetske koordinate.
Na kraju treba reći da se duljine i površine mogu određivati mjerenjem na kartama u bilo kojoj projekciji ako se pri tome uzimaju u obzir deformacije projekcije. Na taj je način već 1993. određena površina hrvatskog mora i otoka s karte mjerila 1:1 000 000 u Gauss-Krügerovoj, dakle konformnoj, projekciji (Lapaine i dr. 1993).