1. INTRODUCTION
The current research is centred on addressing the critical issues related to Reliability, Availability, and Maintainability (RAM) in process industries where uninterrupted operation and minimal downtime are crucial. Each component of the RAM acronym can be briefly explained as follows[1]:
Reliability is the measure of the probability that a system will operate without failures or breakdowns over a specific period. High reliability indicates that the system is less prone to failures, which is essential for ensuring continuous and stable operations in process industries.
Availability estimates the percentage of time a system or equipment is operational and ready to perform its intended function when needed. High availability means that a system is readily available for use, which is essential in industries where production schedules and processes must be maintained without significant interruptions.
Maintainability refers to the ease with which a system or equipment can be restored to operational status after a failure or breakdown. It includes factors like repairability, the availability of spare parts, and the skills and resources needed for maintenance. High maintainability is essential for minimizing downtime and ensuring all the issues are solved quickly and cost-effectively.
An appropriate modelling technique addressing RAM issues, as highlighted by Narendra et al.[1], can be harnessed for the creation of mathematical models, aiding in practical applications.
The process industries are not only the backbone of both domestic and global markets but also play a pivotal role in shaping a country's economic well-being, significantly impacting its Gross Domestic Product (GDP). Over the past few decades, rapid transformations in various scientific domains have placed significant pressure on these industries to meet continuously evolving customer demands. At times, certain regulatory norms and restrictions on health, safety, and quality imposed by governments have also compelled them to incorporate essential parameters such as Safety, Quality, Cost, Deliverability, and Reliability into their inherent operational strategies.
The contemporary hybridized model of the global market has transformed the business environment like a game of snakes and ladders, where quick peaks and falls are possible. However, it has also opened doors to infinite opportunities.
The framework of this case study is intended to introduce an interdisciplinary scientific approach to solving real-world industrial RAM problems. Employing rigorous effort while modelling complex systems helps in achieving sustainable solutions. Such studies offer valuable insights for addressing the situation at hand. The following sections will cover various aspects of this study, including the literature review, the framework with system descriptions, performance modelling, a discussion of results, and a summary of the key findings and contributions.
2. LITERATURE REVIEW
Recent years have seen substantial research contributions in the field of RAM processes from both researchers and practitioners. These efforts have significantly aided in advancing the growth and development of process industries. Below are highlighted noteworthy works addressing these industrial issues.
Goel[2] emphasised certain important factors that might be helpful while selecting an appropriate technique for modelling system behaviour. These factors are:
Singh and Garg[3] used Markov approach for the availability assessment of the veneer-making system of the plywood industry. Sharma and Kumar[4] applied Markovian approach to developing a mathematical model of the systems of a urea manufacturing plant. Sachdeva et al[5] applied Petri nets for the modelling of the pulping unit of a paper manufacturing plant. Gupta and Tewari[6] used Markov chains for the modelling of the different systems of a coal-based power plant.
Thangamani[7] applied Generalized Stochastic Petri nets for the modelling and analysis of a lube oil system of a combined cycle thermal power plant. Ranjan et al[8] developed a competing risk model using Markov process considering exponential failure distribution. The obtained results would be helpful in minimizing the risks associated owing to both aging and accidental failures of industrial systems.
Aggarwal et al[9] performed a RAM assessment of the skim powder-making system of a milk plant. Markov birth-death technique has been used for developing mathematical models of the systems and sub-systems.
In recent years, Malik and Tewari[10,11] developed performance models using Markov chains for different systems of a thermal power plant. Further particle swarm optimization (PSO) technique has been applied for optimizing the results. Li et al[12], Kumar et al[13,14,15,16], Kuchárik and Balogh[17], Kumar and Tewari[18] and Parkash and Tewari applied[19] extended versions of PN based approach for developing performance models of different industrial systems.
More recently, Farahani et al[20] described the use of Markov chains to carry out the analysis of time-dependent behaviours of the system and to predict the probable failure nature of industrial systems. Malhotra[21] developed a generalized method based on Markovian approach to determine different measures such as transition probabilities, mean time to failure, reliability, and availability for a two-unit cold redundant system with varied demand. Nivas[22] proposed a Markov model to compute the system reliability and profit analysis on which the decision to offer a cost-free warranty for users is based.
The above-discussed literature on RAM practices reveals that these state space modelling tools are highly efficient and accurate in their performance while also reducing computational efforts. These tools can effectively address complex RAM issues such as failure and repair dependencies, and share maintenance facilities for different units that have different effects and different resource requirements. In such situations, Markov process and Petri Nets are preferred. In this particular study, the Markov process is employed for modelling purposes. These two modelling techniques may be briefly described as follows:
Markov method is indeed a powerful modelling and analysis tool with various applications, including the analysis of time-based reliability and availability. It is commonly used in engineering, economics, and various other fields to study systems with dynamic states and transitions over time. It considers various states, including full operating conditions, reduced modes of operation, and failed states, represented by circle, oval, and rectangle shapes, with each state transition depicted by an arrow, as illustrated in Figure 4.
Petri nets (PN) are a bipartite graphical modelling tool comprising places, transitions, arcs, and tokens represented by circles, rectangles, and arrows. Tokens are positioned within places and transition between places is enabled through arcs. Adam Petri introduced this influential modelling technique in 1962. Today, it boasts several extensions that enhance its capabilities and is facilitated by software tools that streamline modelling and computations.
3. FRAMEWORK OF PRESENT RESEARCH WORK
The essential steps, necessary for the modelling and analysis of a system, are illustrated in the block diagram shown in Figure 1.
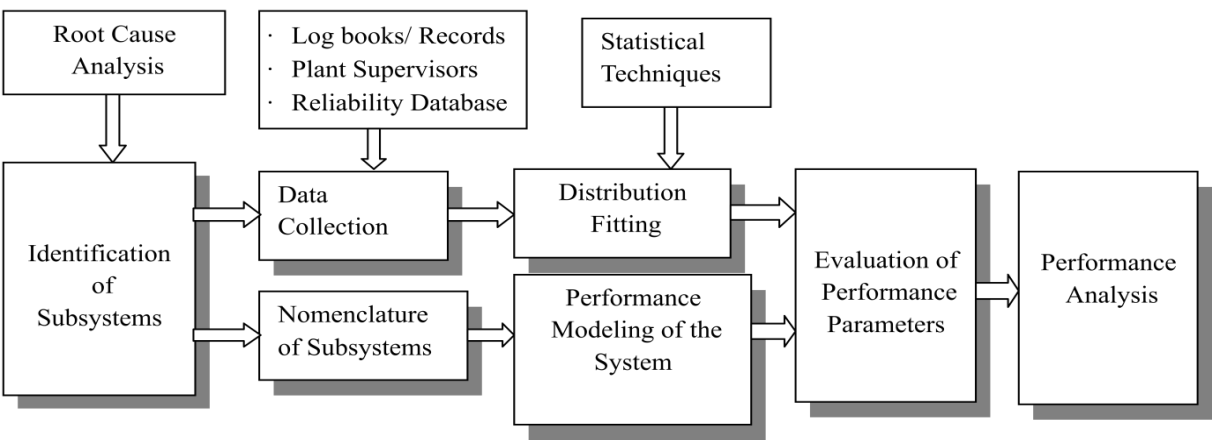
Fig. 1 Framework for the performance modelling and analysis
In this approach, the case study begins by selecting the system, identifying its subsystems, and specifying their nomenclatures. A Root Cause Analysis (RCA) is conducted for every component, as illustrated by the RCA diagram shown in Figure 2. A list of probable causes and symptoms of failure is prepared. Failure and repair data are obtained from the plant in consultation with experienced plant officials. As the collected data might not be in an appropriate order, it is fitted into appropriate continuous time distribution using an appropriate statistical approach such as the least squares method as recommended by Ebeling[23]. An illustrative example of the data fitting concept is explained in Section 5.
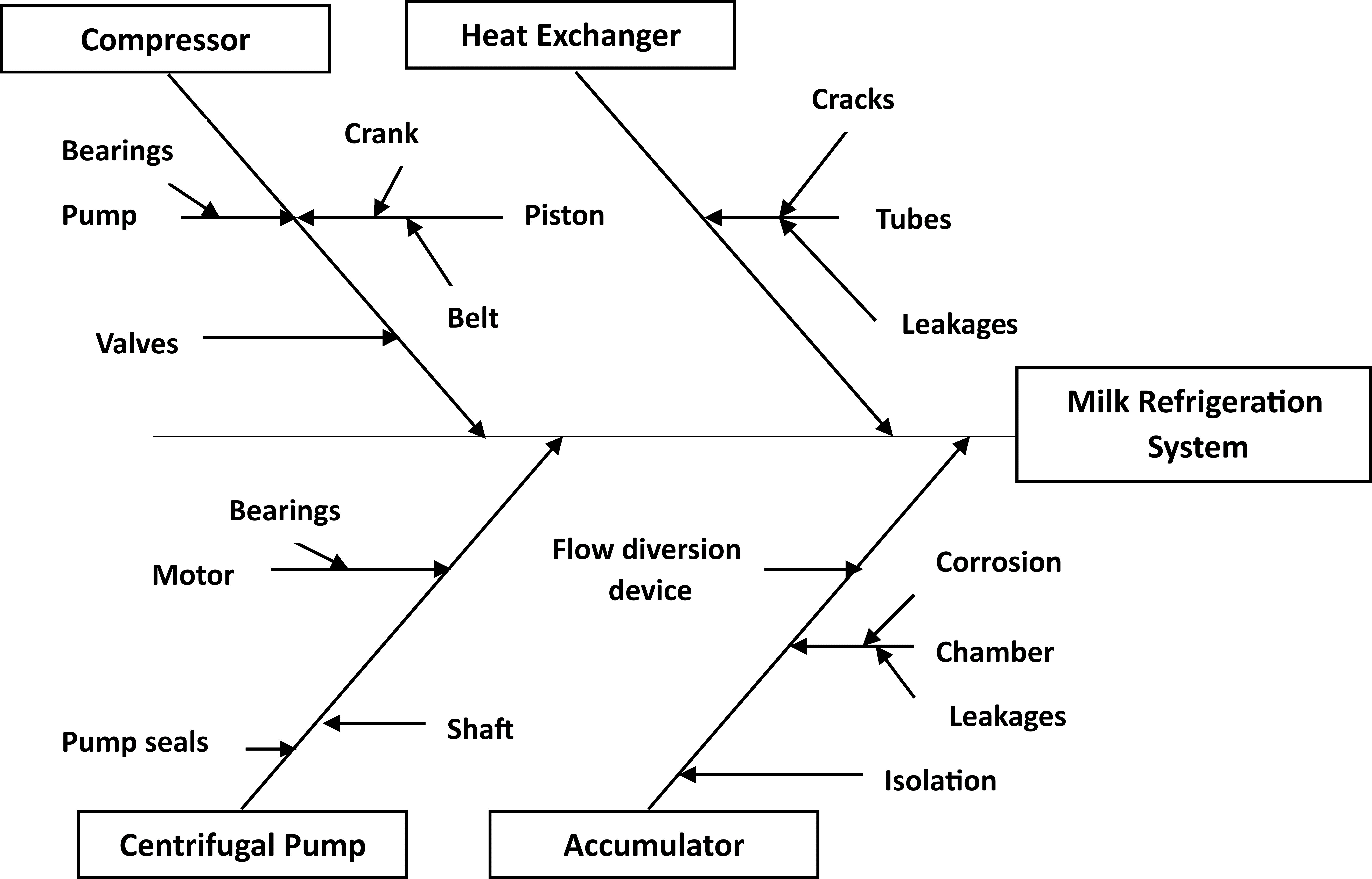
Fig. 2 Root cause diagram of the milk refrigeration system
3.1 SYSTEM DESCRIPTION
The present study intends to identify some critical performance issues of a live industrial system using a suitable and efficient analytical modelling technique. A reputed milk processing plant situated in Ambala, India, has been chosen as the case study. One of its major functional units is refrigeration, which is the breath of the milk plant. Its failure may critically affect the quality of the milk products. The flow diagram of this system consists of several main subsystems as shown in Figure 3.
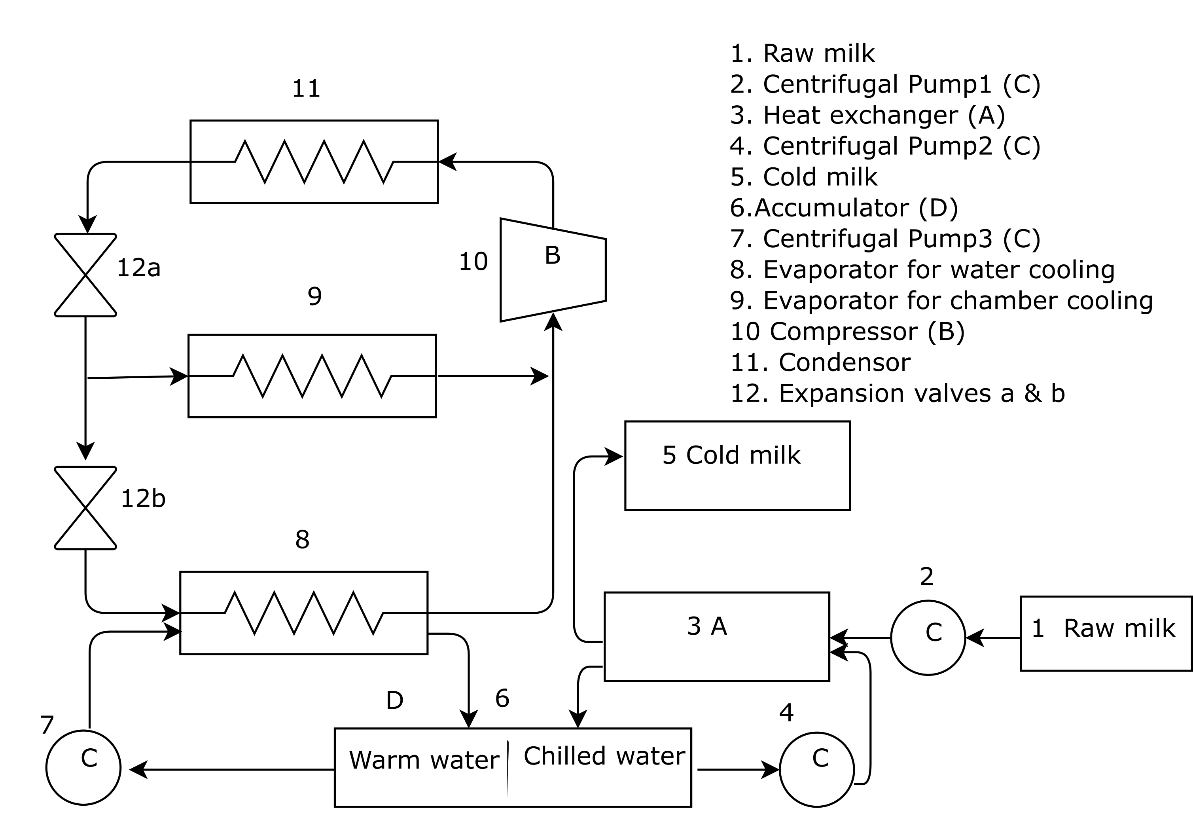
Fig. 3 Flow Diagram of the Refrigeration System
The Milk Refrigeration system, reported in this work comprises four sub-systems namely Heat Exchanger (A), Compressor (B), Centrifugal Pumps(C), and Accumulator (D) out of which Compressor and Pumps are essentially supported with stand by units. Later two sub-systems may also be operated with reduced capacities. The performance modelling is carried out for these sub-systems that are prone to failure. The specific notations and symbols used for its sub-systems are described as:
4. PERFORMANCE MODELLING AND ANALYSIS
In order to develop a mathematical model of the milk refrigeration system Stochastic Markov approach has been applied. Required failure and repair data were obtained from the plant in consultation with experienced maintenance personnel. These are shown in Table 1.
Table 1 Failure and repair data of milk refrigeration system
Assumptions
While developing a performance model of the system under study, certain assumptions have been made. These are:
With the above assumptions and notations, a transition diagram of the system has been developed, as shown in Figure 4.
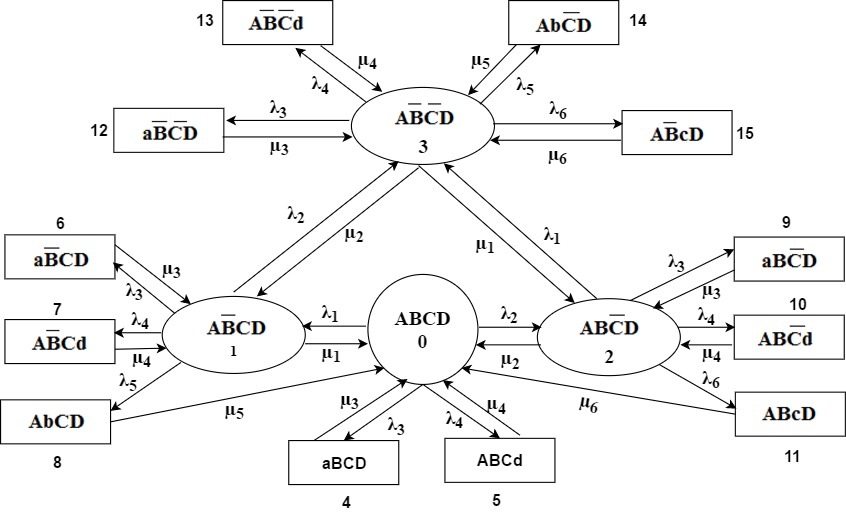
Fig. 4 Transitions diagram of milk refrigeration system
A set of ordinary differential equations is written from the transition diagram shown in Figure 4. These may be obtained with two possible situations, namely transient and steady states.
Transient state
Steady-state
Steady-state equations can be obtained by imposing the condition that:
Limit t→ ∞, Limit d/dt→0.
Now, Eqs. (1) to (8) reduce to the following equations:
Table 2 System’s availability with varying failure (λ1) and the repair (µ1) rates of ‘compressor’
Table 3 System’s availability with varying failure (λ2) and the repair (µ2) rates of ‘centrifugal pumps’
Table 4 System’s availability with varying failure (λ3) and the repair (µ3) rates of ‘heat exchanger’
Table 5 System’s availability with varying failure (λ4) and the repair (µ4) rates of ‘accumulator’
Fig. 5 Effects of the failure and the repair rates of ‘compressor’ on the availability
Fig. 6 Effects of the failure and the repair rates of ‘centrifugal pumps’ on the availability

Fig. 7 Effects of the failure and the repair rates of ‘heat exchanger’ on the availability
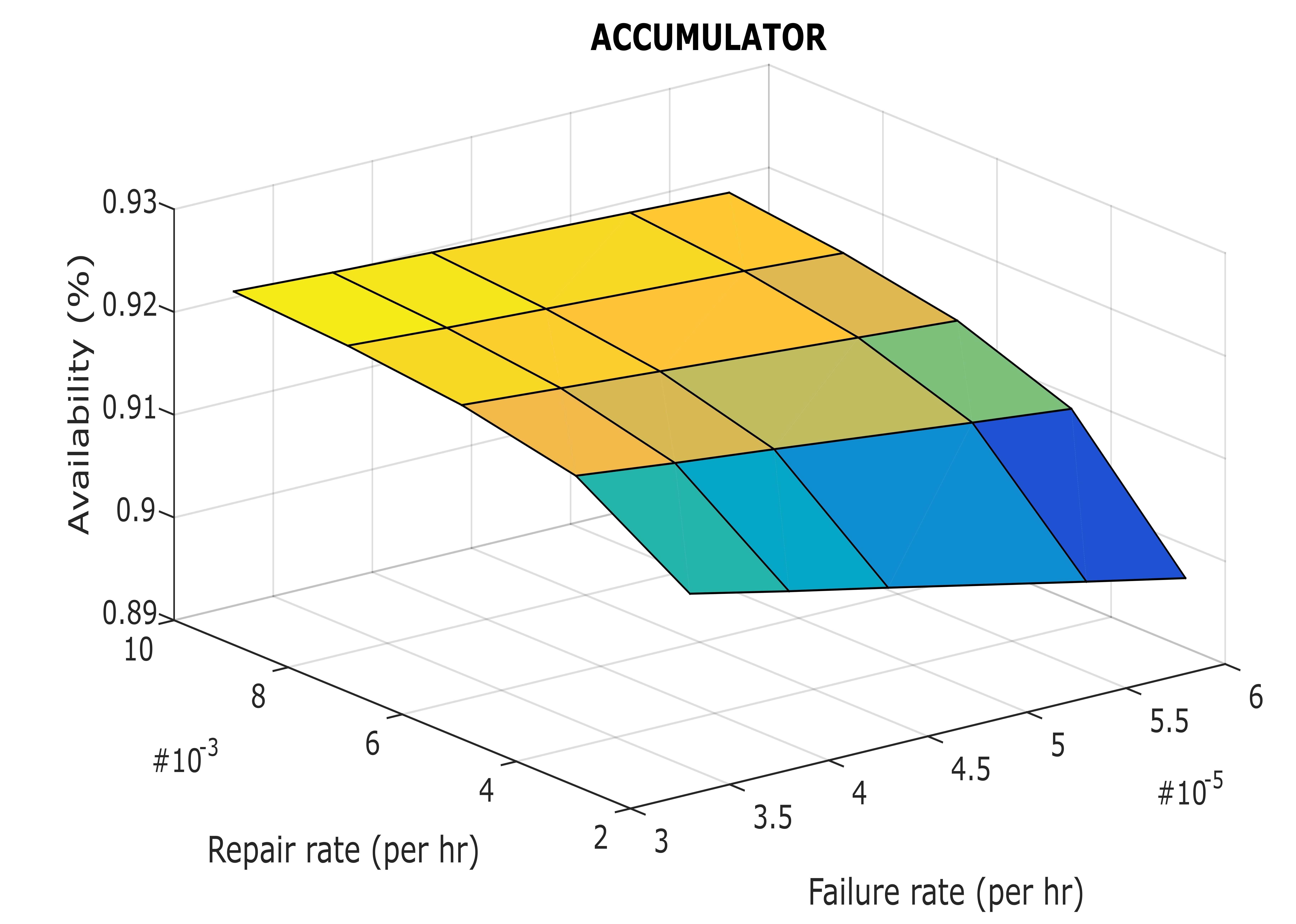
Fig. 8 Effects of the failure and the repair rates of ‘accumulator’ on the availability
5. DISCUSSION OF RESULTS
In the present study, an exponential pattern of both failure and repair data has been assumed. In an exponential distribution, the mean time to failure (MTTF) is equivalent to the reciprocal of the mean failure rate (λ), and the mean time to repair (MTTR) is equivalent to the reciprocal of the mean repair rate (µ).
Mathematically expressed, MTTF = 1/λ and MTTR = 1/µ.
In order to best fit the data into an exponential distribution, the least square method was used, resulting in a regression line in the form of Y = α + βx, where α represents the Y-axis intercept, and β is the slope of the line.
The values of α, β, λ and µ could be efficiently determined by writing a simple computer program using MATLAB software tool, separately used for failure and repair data.
For ease of understanding an illustrative computer program is written that may be suitably used for computation of both MTTF and MTTR for any of the defined systems or subsystems. This is as under:
Suppose the times when a particular system operates and subsequently fails have been recorded as 1000 hrs, 1100hrs, 1050 hrs, 1500hrs, 1200hrs, 870 hrs, 981hrs,1352 hrs,1021hrs, 1052 hrs. Its computer program for MATLAB environment may be written in the following steps:
Step 1: Formation of a data matrix
% Given failure times
Failure times = [1000, 1100, 1050, 1500, 1200, 870, 981, 1352, 1021, 1052];
Step 2: Use ‘polyfit’ function for linear regression
% Perform linear regression using polyfit with degree 1
x = 1: length(failure_times);
p = polyfit(time_points, log(failure_times), 1);
Step 3: Syntax for determining slope and intercept of regression lone
% Extract slope (beta) and intercept (alpha)
beta = p(1);
alpha = p(2);
Step 4: Syntax for computing failure rate and MTTF
% Calculate lambda and MTTF
lambda = -beta;
mttf = 1 / lambda;
Step 5: Syntax for results display
% Display the results
disp(['Estimated failure rate (lambda): ', num2str(lambda)]);
disp(['Mean Time to Failure (MTTF): ', num2str(mttf), ' hours per failure']);
Availabilities of the system with different failure (λ) and repair (µ) values of various sub-systems within permissible ranges are obtained from Eq. (20).
MATLAB software package was used for getting accurate and fast analytical results along with high-quality 3D illustrative plots. These are presented in Tables (2 to 5) and Figures (5 to 8).
A permissible variation in failure rates of different subsystems revealed that the heat exchanger and centrifugal pumps both have nearly equal but significant effects on the performance of the system. It may be clearly understood from Figures 6 and 7 and Tables 3 and 4. The observed variations in availabilities of heat exchangers and pumps are 8.88 and 8.86 % respectively. A moderate effect was noticed with the compressor which varies the availability of the system by 4.16%. The variation in failure and the repair values on the accumulator shows the least effect as much as 2.13%. Narendra et al[13] observed almost similar effects on the system’s behaviour with the PN approach. Based upon the above discussions, a framework on DSP may be proposed for the guidance of the users facing RAM issues. This is presented in Table 6.
Table 6 Proposed Framework on Decision Support Priorities
*Currently being managed based on intuitive decisions of the plant managers
6. CONCLUSIONS
A comprehensive study has been carried out considering the live industrial system as a case study. A detailed analysis of the obtained results might be helpful in identifying specific RAM issues that can ultimately impact profitability. The obtained results also revealed that the critical units/subsystems that have more impact on the variation of failure and repair parameters should be on top of maintenance priories.
Kumar and Tewari[13] observed similar effects while solving the same system with the Petri nets approach under similar parametric conditions.
However, certain limitations and difficulties are encountered while using the Markov approach, such as network explosion, even when dealing with a small unit. These difficulties can be effectively addressed through the Petri nets modelling technique or by applying the method for reducing the excessive number of states proposed by Knegtering and Brombacher[24].
Finally, a framework for decision priorities support has been proposed for practitioners. This framework would assist in making decisions regarding maintenance priorities and in establishing a trade-off between investment and profitability while maintaining quality and safety standards with enhanced plant availability.
