1. UVOD
Sigurnost na radu ima posebno značajnu ulogu u radu lučkih sustava.
Strategija postignuća cilja „bez ozljeda na radu“ zasniva se na: stalnom osposobljavanju zaposlenih uz precizna zaduženja i odgovornosti svih sudionika u procesu rada, naročito voditelja poslova: grupovođa, disponenata, organizatora rada, nadzornika, planera, voditelja službi i direktora. Sve se ovo treba ostvariti primjerenom organizacijom rada, ali i provedbom poslova zaštite na radu, što posebno uključuje analizu ozljeda na radu.
Podaci o nezgodama na radu u poduzeću „Luka Rijeka” d. d. obrađuju se na nekoliko razina primjene statistike.
A) razina predstavlja sređivanje raznih podataka o nezgodama u određene klase i utvrđivanje brojčanih odnosa u pojedinim klasama na temelju njihove učestalosti, npr. pokazivanje broja nezgoda po danima u tjednu, satima u tjednu, radnim jedinicama i sl.
B) razina predstavlja svođenje broja nezgoda na manji broj reprezentativnih vrijednosti, primjerice, izražavanje nezgoda u indeksima učestalosti i indeksima težine po radnim jedinicama i sl.
C) razina predstavlja ispitivanje i provjeravanje različitih hipoteza radi otkrivanja stupnja veze između različitih pojava, primjerice, provjeravanje postoji li i u kakvoj mjeri veza između učestalosti nezgoda i stupnja kvalificiranosti radnika, radnog iskustva itd.
U ovom radu autori obrađuju podatke o nezgodama pri radu na A razini. Cilj ovog rada je primjenom odgovarajuće statističke metode, prikazati analizu ozljeda na radu te na taj način ukazati na potrebu sustavnih istraživanja sa svrhom daljnjeg smanjenja ozljeda na radu u lučkim procesima. Postavljena je hipoteza: sustavna istraživanja ozljeda na radu vode značajnom smanjenju ozljeda. Detaljnom analizom pruža se stručnjacima zaštite na radu mogućnost da detektiraju uzrok i izvor ozljede te spriječe njezino ponavljanje.
Posebnu poteškoću u proučavanju nezgoda čini nemogućnost neposrednog prenošenja iskustva na sličnu situaciju. Naime, na prvi pogled minimalna razlika u uvjetima rada može biti veoma značajna u pogledu učestalosti nezgoda. Tako se u identičnim objektivnim prilikama rada dvije skupine radnika mogu značajno razlikovati po učestalosti nezgoda, što može nastati kao posljedica razlike u stavovima prema mjerama zaštite na radu ili zbog drugih subjektivnih razloga.
Ovaj rad temelji se na godišnjem izvješću o zaštiti na radu Luke Rijeka (Milojica, 2013) gdje je korištena Poissonova distribucija kao statistička metoda pri analizi ozljeda na radu. U pripremi ovoga rada izvedena su istraživanja koja se odnose za period od tri godine, tj. od 2011. do 2013. godine.
2. METODOLOGIJA ISTRAŽIVANJA
U ovom radu kao statistička metoda uzeta je Poissonova distribucija koja podrazumijeva raspodjelu rijetkih slučajnih događaja kod kojih je vjerojatnost pojavljivanja vrlo mala.
Ona izražava vjerojatnost broja događaja ako se oni pojavljuju u fiksnom vremenskom periodu s poznatom prosječnom brzinom pojavljivanja i vremenski su nezavisni od prošlog događaja.
Za razliku od normalne distribucije koja je potpuno definirana aritmetičkom sredinom i standardnom devijacijom, Poissonova distribucija je potpuno definirana aritmetičkom sredinom jer je njena varijanca jednaka aritmetičkoj sredini.
Kada je N (ukupan broj) vrlo velik, Poissonova distribucija se približava binomnoj, ali je razlika u tome što kod binomne raspodjele znamo koliko se puta neki događaj pojavio, ali i koliko se puta nije pojavio, a kod Poissonove raspodjele znamo samo koliko se puta neki događaj pojavio.
3. DISTRIBUCIJA BROJA OZLJEDA NA RADU U DIONIČKOM DRUŠTVU „LUKA RIJEKA“ ZA PERIOD OD 2004. DO 2013. GODINE
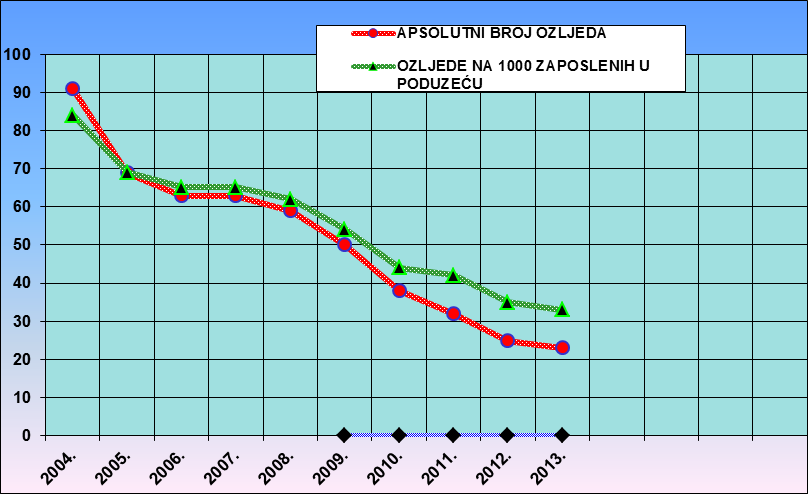
Iz tablice je vidljivo da se broj zaposlenih iz godine u godinu smanjivao i da je dolazilo do pada apsolutnog broja ozljeda . U promatranom razdoblju u 2013. godini dogodio se najmanji broj ozljeda na radu, tj. 8 % manje nego u 2012. godini i 6 % manje ozljeda na 1.000 zaposlenih u odnosu na 2012. godinu. Isto je zorno prikazano ugrafikonu 1.
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
4. ISPITIVANJE PRIMJENJIVOSTI POISSONOVE RAZDIOBE
Obično se pretpostavlja da je razdioba broja ozljeda dobro opisana teorijskom Poissonovom razdiobom. U pripremi ovoga rada izvedena su proučavanja koja se odnose za period od tri godine, tj. od 2011. do 2013. godine.
4.1 Primjena c2 testa
c2(hi–kvadrat) test isključivo se primjenjuje na podacima predstavljenim frekvencijama dobivenim brojenjem (f) ili teorijskim izračunavanjem (ft) prema nekom modelu distribucije frekvencija (normalna, binomna, Poissonova, negativno binomna).
Vrijednost c2 mjera je odstupanja stvarnih, opažanih frekvencija (f) od teorijskih očekivanih (ft).
Provjereno je razlikuje li se broj stvarnih frekvencija (ozljeda) u Luci Rijeka statistički značajno od teorijskih očekivanih ozljeda. Provjeravalo se pomoću hi–kvadrat testa.
Vrijednost c2 izračunava se izrazom:
Vrijednost Poissonove razdiobe izračunava se izrazom:
x̄ gdje je : m =
c2 (hi–kvadrat) testom provjereno je razlikuje li se distribucija broja ozljeda na radu u trgovačkom društvu Luka Rijeka u posljednje tri godine značajno od frekvencije teorijske očekivane Poissonove distribucije ozljeda.
Vrijednosti stvarnih frekvencija prikazane su utablici 2.
| godina | broj radnika | ||
|---|---|---|---|
| broj ozljeda | s jednom ozljedom | s dvije ozljede | |
| 2011. | 738 | 28 | 2 |
| 2012. | 700 | 23 | 1 |
| 2013. | 683 | 19 | 2 |
| å | 2120 | 70 | 5 |
| x̄ | 707 | 23,2 | 1,67 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
4.2 Izračunavanje teorijskih frekvencija Poissonove razdiobe
Teorijska frekvencija f (0) izračunava se izrazom:
gdje je:
x̄ = prosječna vrijednost rijetkih slučajeva
k = konstanta koja iznosi 0,4343
n = ukupan broj (å f) slučajeva
Teorijske frekvencije svake sljedeće vrijednosti (x) od 1 na više dobivaju se izrazom:
Uz poznatu vrijednost m (m = 0,0417) moguće je izračunati bilo koju vrijednost P(x) Poissonove distribucije za x = 0,1,2,3, ...
ANALIZA PODATAKA ZA 2011. GODINU
| broj ozljeda (x) | f | f . x | ft | P(x) | f - ft | (f - ft)2 | (f - ft)22 |
|---|---|---|---|---|---|---|---|
| 0 | 738 | 0 | 736,72 | 0,9592 | 1,28 | 1,638 | 0,82 |
| 1 | 28 | 28 | 30,72 | 0,0399 | -2.72 | 7,398 | 3,70 |
| 2 | 2 | 4 | 0,64 | 0,0008 | 1.44 | 2,074 | 1,04 |
| å | 768 | 32 | 768 | 0,9999 | 0 | 5,56 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Na temelju izračunatog stupnja slobode 1 (ss = k - 2) gdje je:
k = broj kategorija (u ovom primjeru to je broj različitih ishoda (k = 3), pa za ovaj primjer broj stupnjeva slobode iznosi: ss = k - 2 = 3 - 2 =1)
Prema dostupnim podacima iz relevantne literature (Šrekl, 1997)očitane su granične c2 vrijednosti. Za 1 % rizika pogreške u zaključivanju granična vrijednost iznosi 6,64, a za 5 % rizika vrijednost je 3,84. Izračunata vrijednost iznosi 5,56, dakle između tabličnih vrijednosti, pa se može tvrditi, uz rizik pogreške u zaključivanju manji od 5 % a nešto veći od 1 %, da ne postoji statistički značajna razlika između empirijskih i teorijskih frekvencija, te da se razdioba ozljeda pokorava zakonu Poissonove distribucije, što je vidljivo nagrafikonu 2.
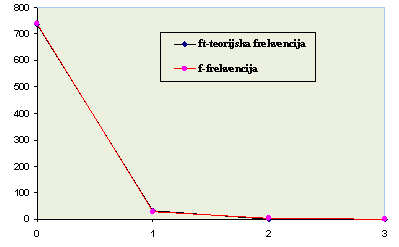
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
ANALIZA PODATAKA ZA 2012. GODINU
| broj ozljeda (x) | f | f . x | ft | P(x) | f - ft | (f - ft)2 | (f - ft)22 |
|---|---|---|---|---|---|---|---|
| 0 | 700 | 0 | 699,52 | 0,9660 | 0,480 | 0,230 | 0,0003 |
| 1 | 23 | 23 | 24,13 | 0,0333 | -1,130 | 1,277 | 0,053 |
| 2 | 1 | 2 | 0,42 | 0,0006 | 0,650 | 0,422 | 1,006 |
| å | 724 | 25 | 724 | 0,9999 | 0 | 1,06 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
c2 = 1,06
ss = 3 – 2 = 1 → iz tablice: za 1 % rizika 6,64
za 5 % rizika 3,84
Na temelju izračunatog stupnja slobode 1, prema dostupnim podacima iz relevantne literature (Šrekl, 1997) očitane su granične c2 vrijednost. Za 1 % rizika pogreške u zaključivanju, granična vrijednost iznosi 6,64, a za 5 % rizika vrijednost je 3,84. Izračunata vrijednost iznosi 1,06, dakle manja c2 < c2 g pa se može tvrditi da nema statistički značajnijih razlika između dobivenih i teoretski očekivanih frekvencija.
ANALIZA PODATAKA ZA 2013. GODINU
| broj ozljeda (x) | f | f . x | ft | P(x) | f - ft | (f - ft)2 | (f - ft)22 |
|---|---|---|---|---|---|---|---|
| 0 | 683 | 0 | 681,35 | 0,9679 | 1,650 | 2,72 | 0,004 |
| 1 | 19 | 19 | 22,21 | 0,0316 | -3,210 | 10,30 | 0,464 |
| 2 | 2 | 2 | 0,36 | 0,0005 | 1,560 | 2,43 | 6,75 |
| å | 704 | 23 | 704 | 1,0 | 0 | 7,22 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
c2 = 7,22
ss = 3 – 2 = 1 → iz tablice: za 1 % rizika 6,64
za 5 % rizika 3,84
Prema dostupnim podacima iz relevantne literature(Šrekl, 1997)očitane su granične c2 vrijednosti. Za 1 % rizika pogreške u zaključivanju, iznosi 6,64, a za 5 % rizika je vrijednost 3,84. Izračunata vrijednost iznosi 7,22, dakle veća je od tabličnih vrijednosti, pa se može tvrditi da postoji statistički značajnija razlika između empirijskih i teoretski očekivanih frekvencija.
ANALIZA PODATAKA ZA RAZDOBLJE OD 2011. DO 2013. GODINE
| broj ozljeda (x) | f | f . x | ft | P(x) | f - ft | (f - ft)2 | (f - ft)22 |
|---|---|---|---|---|---|---|---|
| 0 | 707 | 0 | 706,15 | 0,9646 | 0,85 | 0,72 | 0,0001 |
| 1 | 23,33 | 23,33 | 25,42 | 0,0347 | -2,09 | 4,37 | 0,17 |
| 2 | 1,67 | 3,40 | 0,457 | 0,0006 | 1,24 | 1,54 | 3,42 |
| å | 732 | 26,6 | 732 | 0,9999 | 0 | 3,59 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
c2 = 3,59
ss = 3 – 2 = 1 → iz tablice: za 1 % rizika 6,64
za 5 % rizika 3,84
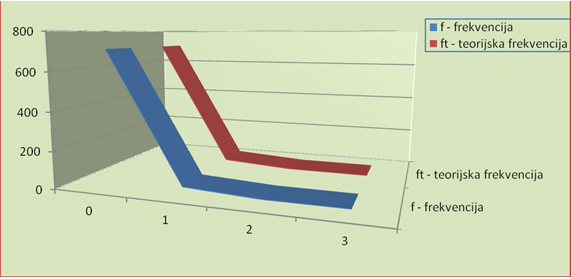
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Zbroj relativnih kvadratičnih odstupanja frekvencija u posljednjem stupcutablice 6 daje vrijednost c2 = 3,59, dok granična vrijednost varijable c2 distribuirane po Poissonovoj razdiobi na razini značajnosti 0,05 za 1 stupanj slobode iznosi 3,84, a na razni značajnosti 0,01 je 6,64. Budući da je c2 < c2 g zaključuje se da nema značajnijih razlika između empirijskih i teorijskih frekvencija, te se razdioba broja ozljeda pokorava zakonu Poissonove razdiobe.
5. RASPODJELA OZLJEDA NA RADU
| smjena | sati rada | dolazak /odlazak/ 1/0 | |||
|---|---|---|---|---|---|
| 0 - 2 | 2 - 4 | 4 - 6 | 6 - 8 | ||
| I. | 2 | 7 | 4 | 4 | |
| II. | 3 | 2 | 0 | 0 | |
| III. | 0 | 0 | 0 | 0 | |
| å | 5 | 9 | 4 | 4 | 1 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
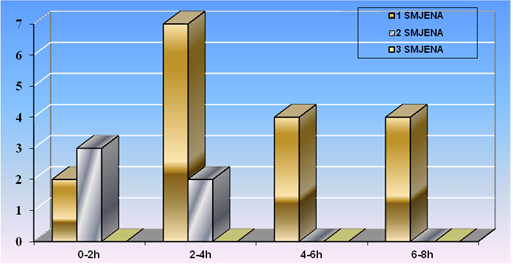
Iz tablice 7 vidljivo je da se, sveukupno gledajući, u 2013. godini ozljede nisu ravnomjerno događale od 0 do 8 sati rada.
Izgrafikona 4 vidi se da se najveći broj ozljeda na radu dogodio u prvoj smjeni između 2 i 4 sata rada, a u drugoj smjeni između 0 i 2 sata rada.
U trećoj radnoj smjeni nije bilo ozljeda na radu.
Opažene frekvencije učestalosti ozljeda (navedene utablici 7) uspoređene su s teorijskim frekvencijama koje su određene u skladu sa statističkom hipotezom, da su ozljede na radu podjednako raspoređene po satima rada. Za utvrđivanje razlika i značajnosti razlika primijenjen je c2 test.
| frekvencija učestalosti ozljeda (f) | ft | f - ft | (f - ft)2 | (f - ft)2/ft |
|---|---|---|---|---|
| 2 | 4,25 | -2,25 | 5,06 | 1,19 |
| 7 | 4,25 | 2,75 | 7,56 | 1,78 |
| 4 | 4,25 | -0,25 | 0,06 | 0,01 |
| 4 | 4,25 | -0,25 | 0,06 | 0,01 |
| 17 | 17 | 0 | c2=2,99 |
Izvor: obrada autora
Uz broj stupnjeva slobode SS = k - 1 = 3 prema dostupnim podacima iz relevantne literature (Šrekl, 1997)očitane su granične vrijednosti c2 . Nalazimo vrijednost 7,82 za 5 % rizika i vrijednost 11,34, za 1 % rizika pogreške u zaključivanju. Izračunata vrijednost iznosi 2,99, dakle manja je od tabličnih vrijednosti, pa se može utvrditi da ne postoji statistički značajna razlika između distribucije broja ozljeda na radu u I. smjeni rada i teorijskih očekivanih frekvencija.
| frekvencija učestalosti ozljeda (f) | ft | f - ft | (f - ft)2 | (f - ft)2/ft |
|---|---|---|---|---|
| 3 | 1,25 | 1,75 | 3,06 | 2,45 |
| 2 | 1,25 | 0,75 | 0,56 | 0,45 |
| 0 | 1,25 | -1,25 | 1,56 | 1,25 |
| 0 | 1,25 | -1,25 | 1,56 | 1,25 |
| 5 | 5 | 0 | c2=5,40 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Prema dostupnim podacima iz relevantne literature (Šrekl, 1997) broj stupnjeva slobode je k = 3, a granična vrijednost c2 na razini značajnosti od 0,05 iznosi 7,82 i vrijednost 11,34 za 0,01. Izračunata vrijednost iznosi 5,40, dakle manja je od tabličnih vrijednosti, pa se može tvrditi da ne postoji statistički značajna razlika između distribucije broja ozljeda na radu koje su se dogodile u II. smjeni rada i teorijskih frekvencija.
| frekvencija učestalosti ozljeda (f) | ft | f - ft | (f - ft)2 | (f - ft)2/ft |
|---|---|---|---|---|
| 5 | 5,50 | -0,50 | 0,25 | 0,05 |
| 9 | 5,50 | 3,50 | 12,25 | 2,23 |
| 4 | 5,50 | -1,50 | 2,25 | 0,41 |
| 4 | 5,50 | -1,50 | 2,25 | 0,41 |
| 22 | 22 | 0 | c2=3,10 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Postavlja se H0(nul - hipoteza) i tvrdi da je učestalost ozljeda na radu po satima rada u ove dvije smjene podjednako raspoređena.
Izračunata c2 vrijednost je 3,10, broj stupnjeva slobode k = 3, kod očitanja iz tablice prema dostupnim podacima iz relevantne literature (Šrekl, 1997) dobiju se vrijednosti za 0,01 (11,34), a za 0,05 (7,82). Prema ovome može se zadržati postavljena H0 –hipoteza i tvrditi da opažana razlika učestalosti ozljeda na radu po satima rada, promatrajući dvije smjene, statistički nije značajna.
6. UČESTALOST OZLJEDA NA RADU PO DANIMA U TJEDNU
Prilikom prikaza učestalosti ozljeda na radu po danima u tjednu broj prisutnih radnika izveden je tako da se uzelo u obzir otprilike 10 % odsutnih radnika zbog slobodnih dana, godišnjih odmora te bolovanja u radnim danima.
Isto tako, zbog djelatnosti koju Luka Rijeka obavlja, uzelo se u obzir otprilike 20 % prisutnih radnika tijekom vikenda.
| Godina | Pon | Uto | Sri | Čet | Pet | Sub | Ned |
| 2004. | 24 | 16 | 13 | 13 | 14 | 5 | 6 |
| 2005. | 18 | 9 | 14 | 11 | 12 | 4 | 1 |
| 2006. | 17 | 8 | 11 | 13 | 10 | 3 | 1 |
| 2007. | 16 | 10 | 10 | 7 | 9 | 4 | 7 |
| 2008. | 18 | 9 | 13 | 7 | 8 | 1 | 2 |
| 2009. | 9 | 11 | 11 | 9 | 6 | 2 | 2 |
| 2010. | 5 | 11 | 8 | 4 | 8 | 0 | 2 |
| 2011. | 8 | 9 | 6 | 4 | 5 | 0 | 0 |
| 2012. | 5 | 6 | 2 | 5 | 5 | 1 | 1 |
| 2013. | 4 | 6 | 4 | 3 | 5 | 1 | 0 |
| UKUPNO | 124 | 95 | 92 | 76 | 82 | 21 | 22 |
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
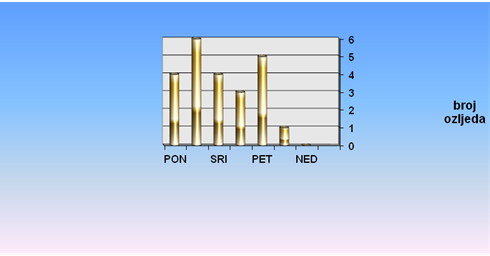
Iztablice 11 vidljivo je da se najveći ukupni broj ozljeda u promatranom razdoblju dogodio ponedjeljkom. Posljednjih 5 godina promatranog razdoblja najveći broj ozljeda događa se utorkom.
Izgrafikona 5 vidi se da se najveći broj ozljeda u 2013. godini, odnosno 48 % od ukupnog broja ozljeda, dogodio utorkom i petkom.
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Uz broj stupnjeva slobode k = 6, granična vrijednost c2 na razini značajnosti od 0,05 iznosi 12,59 i vrijednost 16,81, za 0,01. Izračunata vrijednost iznosi 8,23, dakle manja je od tabličnih vrijednosti, pa se može tvrditi da ne postoji statistički značajna razlika između distribucije broja ozljeda na radu, koje su se dogodile po danima u tjednu, i teorijskih frekvencija.
7. PRIKAZ BROJA OZLJEDA PO MJESECIMA
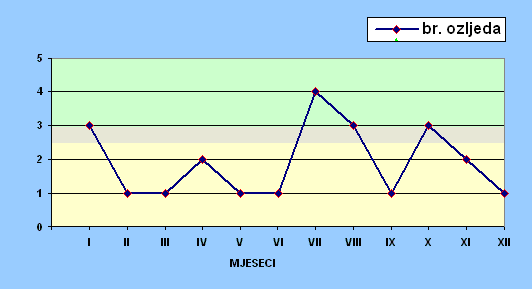
Zbog djelatnosti koju Luka Rijeka obavlja, a to je prekrcaj brodova koji uplovljavaju u luku, prisutan je stalni kontinuitet obavljanja poslova, a to znači da je prisutan podjednak broj radnika po mjesecima, s obzirom na to da su isključeni kolektivni godišnji odmori.
Granična vrijednost c2 na razini značajnosti od 0,05 , kao i ona na razini od 0,01 veća je od izračunate vrijednosti koja je 5,84. Budući da c2 < c2 g zaključuje se da nema statističkih značajnijih razlika između broja ozljeda na radu koje su se dogodile po mjesecima i teorijskih frekvencija, te se razdioba broja ozljeda pokorava zakonu Poissonove razdiobe. Prema tome, odbacuje se nulhipoteza i tvrdi da opažena razlika učestalosti ozljeda po mjesecima u ovom slučaju nije statistički značajna.
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinu
Izvor: obrada autora prema podacima dobivenim iz Izvješća Službe zaštite na radu Luke Rijeka za 2013. godinuu
8. ZAKLJUČAK
Istraživanje primjenjivosti Poissonove razdiobe na empirijsku razdiobu broja ozljeda izvedeno je za sve radnike Luke Rijeka u razdoblju od 2011. do 2013. godine. Za svaku godinu provjereno je razlikuje li se statistički značajnije broj stvarnih frekvencija (ozljeda) od teorijski očekivanih ozljeda. Provjeravalo se pomoću c2 (hi–kvadrat) testa. Ozljede na radu pripadaju rijetkim događajima i za njih se može reći da se raspodjeljuju u obliku tzv. Poissonove distribucije. Poissonova distribucija, slično kao i normalna distribucija, teorijski je model raspodjele nekih obilježja ili događaja. Normalna distribucija je, međutim, simetrična i odnosi se na obilježja koja su isto tako raspodijeljena u populaciji. Poissonova razdioba je uglavnom asimetrična, što je uzrokovano nejednakom vjerojatnošću ostvarivanja nekog događaja, kao što su ozljede na radu. Naime, najvećem broju radnika dogodit će se, u određenom periodu na radu, samo jedna ozljeda, puno manjem broju radnika u istom će se razdoblju rada dogoditi dvije, tri ili više ozljeda. Ozljede u Luci Rijeka mogle bi se distribuirati po Poissonovoj krivulji kada na njih ne bi djelovali nikakvi vanjski ili unutarnji čimbenici, a njih je teško izbjeći. Pod ovim čimbenicima podrazumijeva se organizacija rada pri izvođenju radnog procesa, uređenje mjesta rada, tj. uvjeti rada koji su za luku karakteristični, s obzirom na to da se radi o aktivnostima rada na otvorenom prostoru, zatim osposobljenost radnika za rad na siguran način, ispunjavanje zahtjeva za rad na poslovima s posebnim uvjetima rada u pogledu općih zdravstvenih, psihičkih i psihofizioloških sposobnosti i sl. Radi toga se Poissonova distribucija može primijeniti pri analizi rijetkih događaja kao što su ozljede na radu. Ovi čimbenici su ujedno i ograničenja, odnosno problemi na koje smo naišli prilikom istraživanja. Oni se ne mogu u potpunosti otkloniti, ali se može posvetiti posebna pozornost na njih kako bi se smanjio njihov negativan učinak. Primjenom statističke metode, prilikom analize ozljeda na radu dobili smo smjernice za sustavno istraživanje ozljeda kako bi se „rijedak događaj“ (kako se u praksi definira ozljeda na radu) u potpunosti pokušao eliminirati. Koristeći Poissonovu distribuciju najbolje smo se približili analizi ozljeda s obzirom na to da je ozljeda na radu događaj koji se u praksi rijetko događa, a upravo Poissonova distribucija služi za raspodjelu vrlo rijetkih događaja, kod kojih je vjerojatnost pojavljivanja vrlo mala. S obzirom na sve navedeno smatramo kako analiza ozljeda na radu primjenom Poissonove distribucije može biti temelj, odnosno smjernica za buduća sustavna istraživanja ozljeda na radu po kojoj bi se trebali voditi stručnjaci zaštite na radu kako bi postigli svoj glavni cilj - sigurnost je na prvom mjestu.