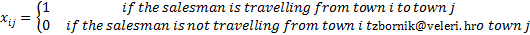1. INTRODUCTION
The Travelling Salesman Problem is one of the most studied problems in mathematical optimization. The possibility to apply this problem to various human activities is what it makes one of the most recognizable mathematical problems without an ideal solution so far.
The formulation of the problem is simple. The travelling salesman needs to pass through several towns and return to the starting point of his travel, making the shortest trip possible. Instead of examining the shortest route, one could examine the one that costs the least, one that allows the greatest flow of information, etc.
By its nature, the TSP falls into the category of NP-complete problems; meaning there is no algorithm that would provide a solution for the problem in terms of polynomial time but if the solution appears, one could test it and conclude whether it is an optimal one.
The goal of this research is to optimize the delivery of packages to appointed addresses in Rijeka. The delivery man has to deliver packages using the most efficient and shortest route moving from the distribution center to which he is required to return to after the delivery of the last package. This is in fact a Travelling Salesman Problem (Bosančić, V. Golemac, A. Vojković T.) and it can be solved using the branch and bound method (Pielić, M).
The paper consists of four parts. The Travelling Salesman Problem as well as the basic definitions of graph theories are provided in the second part. The theoretical basis for the branch and bound method is elaborated in the third part. Along with the theoretical basis, the algorithmic display of the method is provided. In the fourth and final part the method is used on the subject of the research.
2. THE TRAVELLING SALESMAN PROBLEM
In order to use mathematical methods in solving the Travelling Salesman Problem one needs to translate it to the language of a graph theory. The first step is to define several terms (Veljan, D.; Pašagić, H.).
Definition 1.1. Graph 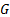 is an ordered pair
is an ordered pair
 where
where
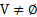 is a set of vertices of the graph while
is a set of vertices of the graph while
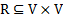 is a set of edges or arcs
of the
is a set of edges or arcs
of the 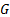 graph.
graph.
In line with the definition, the vertices of graphs will be marked with  , and the edges with
, and the edges with
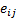 . Mark
. Mark 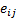 tells us that the given edge is incident (connected) with
the vertices
tells us that the given edge is incident (connected) with
the vertices  and
and 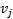 .
.
Definition 1.2. The path in the graph is 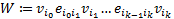 of the string in which all the vertices
are different. The cycle is the path in which
of the string in which all the vertices
are different. The cycle is the path in which 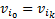 .
.
Definition 1.3. a Hamilton path (cycle) in graph 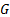 is the path (cycle) that contains
all the vertices of graph
is the path (cycle) that contains
all the vertices of graph 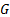 . The graph is called a Hamilton graph if it contains a Hamilton cycle.
. The graph is called a Hamilton graph if it contains a Hamilton cycle.
Definition 1.4. Weighted graph or a network is a graph in which all the edges have their appointed real numbers.
The number  is appointed to the edge
is appointed to the edge 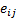 and it is called the weight
of the edge or simply - weight.
and it is called the weight
of the edge or simply - weight.
According to the above mentioned definitions one could conclude that the solution for the Travelling Salesman Problem is equivalent to finding the Hamilton cycle with the least weight in the network.
The Travelling Salesman Problem in its core is a problem of binary linear programming. The following codes are introduced (Perić, T.):
The Travelling Salesman Problem can be written as follows (Perić, T.):
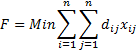

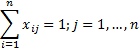
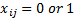
The objective function is marked with F. The limitation should also be included into the program 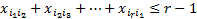 in order to prevent the salesman returning to one of the towns he has already been to before he has visited all the towns. In
other words, with these limitations the possibility of the appearance of under-cycles in the network is prevented. Since
variables
in order to prevent the salesman returning to one of the towns he has already been to before he has visited all the towns. In
other words, with these limitations the possibility of the appearance of under-cycles in the network is prevented. Since
variables 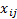 can only take a 0 or 1 state, this problem has a finite number of solutions.
can only take a 0 or 1 state, this problem has a finite number of solutions.
3. THE BRANCH AND BOUND METHOD
While solving the Travelling Salesman Problem two approaches can be used. The first one is to find the correct solution,
the optimal Hamilton cycle in the graph. Generally speaking, this is not so hard to achieve – first one has to find all the
Hamilton cycles and choose the one with the minimal weight (Ivić, M.). However, the problem arises even in the case of a
low number of vertices. Namely, the number of Hamilton cycles in the graph is 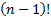 where n
signifies the number of vertices of the graph. Number of cycles possible for
where n
signifies the number of vertices of the graph. Number of cycles possible for 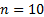 is
362880 while the number of cycles for
is
362880 while the number of cycles for 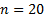 equals 121645100408832000.
equals 121645100408832000.
The complexity of this particular problem is 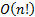 and it is virtually useless when the number of vertices
(entry data) exceeds 10 (Carić, T.).
and it is virtually useless when the number of vertices
(entry data) exceeds 10 (Carić, T.).
The second approach consists of pursuing the “good enough” approximate solution.
The branch and bound method provides a correct solution for the given problem. It is suitable for use when the number of vertices of graphs does not exceed 60, which is sufficient when it comes to problems such as package delivery.
This method is based on the idea that the sets are divided into two disjoint subsets at every step of the process - branching. Furthermore, one subset contains the path between the two selected towns and the other subset does not. For each of these subsets the lower restriction (bound) is calculated for the duration or for travel expenses. Finally, the subset which exceeds the estimated lower bound is eliminated.
The procedure of branching is represented by a tree where the top is marked by the branching points of the set of solutions, and the edges mark the path between the two contiguous vertices in the graph which are used to model the problem and inside which the shortest Hamilton cycle is pursued.
The knots in the branching tree are labelled with the “etiquettes” which represent the lowest binding point for the objective function.
“Weightings” are assigned to the edges and they mark with 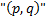 the routes that are travelled or with
the routes that are travelled or with
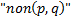 those bypassed.
those bypassed.
A way to represent and use this method with data tables is demonstrated since they are clearly suitable for any future computer applications (Perić, T.).
The steps of the algorithm for the Travelling Salesman Problem using the bound and branch method are as follows:
Step 1: Drawing a table
A table of distance between the given vertices is drawn. The distance between the vertices i and j
are marked with  . If the two vertices are not contiguous they are marked with
. If the two vertices are not contiguous they are marked with
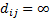 . The
. The 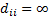 mark to signify and prevent the algorithm to choose
the path
mark to signify and prevent the algorithm to choose
the path 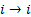 is also appointed.
is also appointed.
Step 2: The reduction of the table
In every row of the table, the smallest element is located and marked with 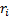 :
:
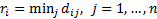
The smallest elements in columns are calculated using the following formula:
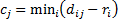
The reduction of the table is calculated with the formula:
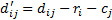
Step 3: The calculation of the lower boundary
The lower boundary of the duration of the travel is calculated
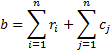
and assigned, which bounds to the knots of the branching tree as etiquette.
Step 3': The calculation of the lower boundary
 is equalized with the etiquette of the knot in which the branching is performed.
is equalized with the etiquette of the knot in which the branching is performed.
Step 4: Branching
The top from which the branching will start is chosen. All the addresses in the reduced table are found, the
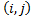 paths, for which we can state that
paths, for which we can state that 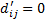 . For each of
these, the “penalty” for not utilizing the trajectory
. For each of
these, the “penalty” for not utilizing the trajectory 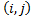 is calculated. The
penalty is calculated with the formula:
is calculated. The
penalty is calculated with the formula: 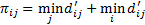
The branching is initiated with the trajectory which is assigned the maximum “penalty”.
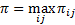
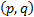 are used to mark the route with the maximum penalty.
are used to mark the route with the maximum penalty.
Step 5: Etiquette calculating
The etiquette of the knot contiguous to the edge which has a “weighting” 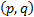 is calculated.
In the reduction table
is calculated.
In the reduction table  is assigned to signify the restriction towards the traveller,
preventing him from returning from town q to town p. Furthermore, all the possibilities
of closing the cycle prior to passing all the vertices of the graph need to be blocked. The next step is to remove
the p line and q column from that table and repeat steps2 and3. The sum of the
reduced elements is marked with
is assigned to signify the restriction towards the traveller,
preventing him from returning from town q to town p. Furthermore, all the possibilities
of closing the cycle prior to passing all the vertices of the graph need to be blocked. The next step is to remove
the p line and q column from that table and repeat steps2 and3. The sum of the
reduced elements is marked with 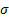 .
.
Step 6: Drawing the branching tree
In the branching tree, we assign the b etiquette to the knot from which the branching started. The edges
that exit this knot are assigned with “weightings” 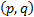 and
and
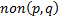 . The
contiguous knot to the
. The
contiguous knot to the 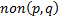 edge is assigned with the
edge is assigned with the
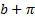 etiquette.
The contiguous knot to the
etiquette.
The contiguous knot to the 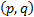 edge is on the other hand assigned with the
edge is on the other hand assigned with the
 etiquette.
etiquette.
Step 7: Locating the knot with the smallest etiquette
One should try to pinpoint the knot with the smallest etiquette in the branching tree and repeat the procedure – steps1-6 are the same with the exception of step3 which is replaced with step3'.
The algorithm is completed when the table contains only routes which, if not used, lead to the solution that is the trajectory of infinite duration.
4. PROBLEM SOLUTION
The aim of this research paper is to optimize the delivery of packages to the appointed addresses in Rijeka. This is in fact a Travelling Salesman Problem and it can be solved using the branch and bound method (Pielić, M). This method is useful when the number of addresses does not exceed 60. In this case the appointed number of addresses is 5 and the method can be applied without the use of computers, as it is shown in the research.
The branch and bound method is used to optimize the package delivery to five addresses in the town of Rijeka. These are the following addresses:
The distance between them in meters is provided inTable 1. (Jozić, F.)
The algorithm described in the previous section is used to calculate the optimal route to deliver the packages to these addresses.
Step 1
| addresses | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 |  | 600 | 1000 | 1900 | 1100 |
| 2 | 600 |  | 1900 | 1900 | 1500 |
| 3 | 1000 | 1900 |  | 1700 | 1200 |
| 4 | 1900 | 1900 | 1700 |  | 1900 |
| 5 | 1100 | 1500 | 1200 | 1900 |  |
Source: authors
Step 2
| addresses | 1 | 2 | 3 | 4 | 5 | 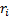 |
|---|---|---|---|---|---|---|
| 1 |  | 600 | 1000 | 1900 | 1100 | 600 |
| 2 | 600 |  | 1900 | 1900 | 1500 | 600 |
| 3. | 1000 | 1900 |  | 1700 | 1200 | 1000 |
| 4 | 1900 | 1900 | 1700 |  | 1900 | 1700 |
| 5 | 1100 | 1500 | 1200 | 1900 |  | 1100 |
Source: authors
The minimal element in the i-row, i = 1,…, 5, calculated using the formula:
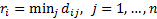
| addresses | 1 | 2 | 3 | 4 | 5 | 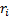 |
|---|---|---|---|---|---|---|
| 1 |  | 600 | 1000 | 1900 | 1100 | 600 |
| 2 | 600 |  | 1900 | 1900 | 1500 | 600 |
| 3. | 1000 | 1900 |  | 1700 | 1200 | 1000 |
| 4 | 1900 | 1900 | 1700 |  | 1900 | 1700 |
| 5 | 1100 | 1500 | 1200 | 1900 |  | 1100 |
 | 0 | 0 | 0 | 700 | 200 |
Source: authors
The minimal element in the j-row, j = 1,…, 5, calculated using the formula:
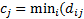 -
- 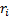 ).
).
| addresses | 1 | 2 | 3 | 4 | 5 | 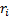 |
|---|---|---|---|---|---|---|
| 1 |  | 0 | 400 | 600 | 300 | 600 |
| 2 | 0 |  | 1300 | 600 | 700 | 600 |
| 3. | 0 | 900 |  | 0 | 0 | 1000 |
| 4 | 200 | 200 | 0 |  | 0 | 1700 |
| 5 | 0 | 400 | 100 | 100 |  | 1100 |
 | 0 | 0 | 0 | 700 | 200 |
Source: authors
The reduction of thetable is done using the formula: 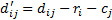 .
.
Step 3
Instep 3, the lower boundary of the duration of the travel route is calculated using the formula
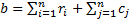 and the result is:
and the result is:
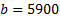
Step 4
The top from which the branching will commence is found. “Penalty” for not using the route i-j is calculated using the formula:
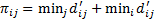
The branching commences with the route that carries the maximum “penalty“ provided by the formula
𝜋=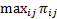 .
.
In this case, the maximum “penalty” is appointed for not using the 2-1 route and it is 600 meters:
 ,
, 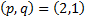
Step 5
The second row and first column are removed from the starting table given the fact that the route 2-1 has the maximum penalty.
This table is then repeatedly used through steps2 and3 producingTable 5. In thistable, the elements from column
 and row
and row  are aggregated.
Their sum is marked with σ. When σ is
aggregated with the lower boundary b calculated in step 2, the lower boundary of the route i-j, in this case
2-1, is calculated.
are aggregated.
Their sum is marked with σ. When σ is
aggregated with the lower boundary b calculated in step 2, the lower boundary of the route i-j, in this case
2-1, is calculated.
| addresses | 2 | 3 | 4 | 5 |  |
|---|---|---|---|---|---|
| 1 |  | 400 | 600 | 300 | 300 |
| 3. | 900 |  | 0 | 0 | 0 |
| 4 | 200 | 0 |  | 0 | 0 |
| 5 | 400 | 100 | 100 |  | 100 |
 | 200 | 0 | 0 | 0 |
Source: authors
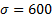
Step 6
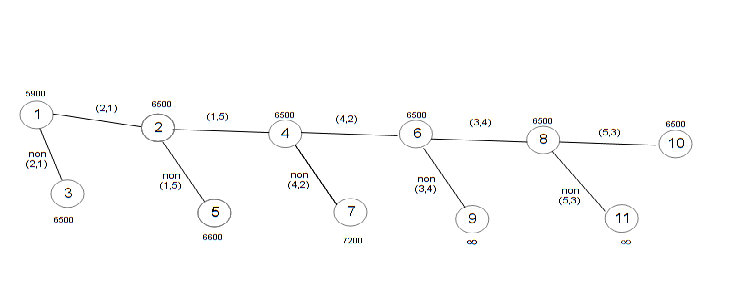
In the branching tree, the top is marked with 1 and the edges that stem from it have “ponders” (2,1) or rather non(2,1) depending on the usage of the route 2-1 for package delivery. The edges end with points 2 and 3. A mark is assigned to each point representing the lower boundary of the route depending on the use or non-use of the given route.

Step 7
The branching is continued in any of the knots, 2 or 3, since their etiquettes have equal values. The calculation is continued in knot 2.
After applying the described procedure four (4) times,Table 6 is provided:
The complete branching tree is represented inPicture 1.
It is concluded that 1 – 5 – 3 – 4 – 2 – 1 is the optimal route for the travelling salesman delivering to appointed addresses. Duration of the route is 6500 meters.
5. CONCLUSION
In this paper we have shown a way to solve the Travelling Salesman Problem by using data tables and the branch and bound method which have given the correct solution to the problem and have proven to be effective in up to 60 data entries. The method to solve the specific problem of package delivery to certain addresses knowing the exact distance between these addresses is used in this example.
By using this method, the optimal package delivery route as well as the duration of this route in meters is calculated. This research has demonstrated that a method to calculate optimal routes, used in this manner and without the use of computers and software packages, can be efficient.
In the context of competitive market it is important to rationalize every business segment by using mathematical methods such as this one. Rationalization by calculation of optimal routes of delivery is very simple to use and it reduces business costs considerably.
The Travelling Salesman Problem can be used widely in many human activities. One of the more important ones could be organizing the production and locating the most optimal sequence of operations and tasks. The sequence of implementing certain automated operations like drilling holes in printed circuit boards is one of the most important ways of optimizing the production process with the Travelling Salesman algorithm.
The branch and bound method is suitable for working with computer applications and it is considered to be one of the possible ways to encourage further exploration of this problem.