INTRODUCTION – Uvod
Human-related factors such as rapid population growth from past to present, industrialization, agricultural activities, mining, utilization of forests and forest products, have led to an increased pressure on ecosystems. This has resulted in changes, destruction, and degradation of forest ecosystems. Particularly, it is known that deforestation is at a very severe scale even in important forest ecosystems such as the Amazon forests in Brazil (Malhi et al., 2008), Colombia (Armenteras et al., 2006), and mangroves (Blanco et al., 2012; Jones et al., 2014) due to agricultural activities, smuggling, timber production etc. Similarly, the fact that rural people in Türkiye usually live in forests or areas adjacent to forests increases the pressure on forest ecosystems. This also applies to the ecosystems in the Mediterranean region, which have been exposed to severe degradation and damage for centuries. As a result of this, most forest ecosystems in the Mediterranean region have become semi-natural ecosystems. Combined with climate change, these ongoing human-related degradations have resulted in decreased biological diversity, reduction in the carbon storage capability of ecosystems, losses in food cycle, erosion, soil and air pollution, habitat losses and fragmentation, reduction in the number of individuals or dislocation of flora and fauna (Hobbs, 1994; Matthews et al., 2000).
In conclusion, it is imperative to develop ecosystem-based management plans aimed at protecting and improving ecosystems to ensure their sustainability. Within this scope, the concept of ecological restoration in forest ecosystems comes to the fore. Jackson et al. (1995) defined ecological restoration as the repair of the human-related damage on the ecosystem diversity and dynamics. Information about the relationships of living organisms with their environment is of great importance to repair the damage, destruction, and degradation of an ecosystem. Therefore, one of the most important steps of ecological restoration is to identify the environments that species can adapt to. For that reason, the ecological features of the species that compose an ecosystem should be identified and mapped. To this end, geographical information systems and modelling methods are the most important tools used for obtaining this ecological information.
Species distribution models are divided into two groups: mechanistic methods and correlative approaches. Mechanistic methods are based on the ecophysiological features of the species to determine their geographical distribution, while correlative approaches model the binary data of the dependent variable or presence-only data according to the environmental factors. If the dependent variable consists of binary data, group discrimination techniques (logistic regression, discriminant analysis, classification tree, generalized additive model, generalized linear model, random forest, artificial neural network, boosted regression trees, multiple linear regression etc.) are used, but if it consists of presence-only data, profile techniques (maximum entropy, genetic algorithm for rule‐set prediction, DOMAIN, ENFA etc.) are used (Beerling et al., 1995; Caithness, 1995; Robertson et al., 2003; Brotons et al., 2004; Mateo et al., 2010; Özkan et al., 2015; Mert et al., 2016; Shabani et al., 2016). Correlative methods are preferred in the species distribution models, and target species may include tree or plant species, wild animals, insects, fungi, birds, or reptiles (Ortega-Huerta and Peterson, 2008; Kramer‐Schadt et al., 2013; Sarmiento-Ramírez et al., 2014; Filz and Schmitt, 2015; Rameshprabu and Swamy, 2015; Mert and Kıraç, 2019). In recent years, species distribution models have been used for various purposes such as restoration, planning, protection and sustainability of ecosystems, monitoring, wildlife management, identification of different habitats, planning of endemic or rare species, climate change crisis, assessment of biological diversity and similar (Franklin et al., 2013; Hamann and Aitken, 2013; Fajardo et al., 2014; Ramirez-Villegas et al., 2014; Mert et al., 2016).
There are several methods and approaches regarding species distribution models (Ferrier et al., 2002; Phillips et al., 2006; Austin, 2007). Methods that have different predictions in ecosystem studies especially play an important role for the explanation or interpretation of relations. As a matter of fact, the relationships in natural ecosystems may not always be linear. They are usually imbalanced, incomplete and complicated; therefore, non-parametric methods should be used to determine such relationships (De’ath and Fabricius, 2000; Cutler et al., 2007; Özkan, 2012a).
Due to different topographical features and local climate types even at short distances, forest ecosystems in the Mediterranean region of Türkiye are complicated. This is why this region is rich in plant diversity and contains many main forests tree species. Gölhisar district is in the mountainous and karstic area of the Mediterranean region. Thus, it has a high species diversity. Gölhisar is an old settlement area that was established around 200 BC. People in this locality were engaged in forging, agriculture, horse and animal raising, wild animal hunting and timber production under the Roman rule (Özüdoğru, 2018). The forest ecosystems have been severely damaged due to the utilization of forests in this area for centuries. Main forest tree species play a crucial role for the continuity of utilization in forest ecosystems. In this context, Brutian pine (Pinus brutia Ten., also known as Turkish red pine) is one of the species with the widest distribution in Türkiye and is among the species that are preferred from a functional perspective. This s because Brutian pine in Türkiye plays an important role in ecosystem-based functional planning for the reduction of effects of climate change, protection of biological diversity, afforestation, ensuring the sustainability, etc. Due to its significance as a key forest tree in Türkiye, this species was utilized more extensively. Although Brutian pine is distributed in a relatively small area in the Gölhisar district, it has an important place in utilization. Brutian pine stands that have a production function in the area are not only utilized for economic purposes but are also used for non-wood products such as resin, root wood, and firewood. On the other hand, there is a Brutian pine gene conservation forest around Gölhisar and Gölova. Gene conservation forests, seed stands, and seed orchards are needed for successful afforestation. In this regard, Brutian pine trees that are distributed up to an elevation of around 1600 m in the locality have an important role in genetic improvement studies (Carus and Çatal, 2012). The utilization of Brutian pine stands for ecological and economic purposes in the district necessitates the protection and ensures the sustainability of Brutian pine ecosystems. Therefore, Brutian pine is one of the crucial species for the ecology-based functional planning of the locality, while one of the priorities should be to identify the locations appropriate for its distribution for effective protection and sustainability.
In the study conducted in the Gölhisar district to achieve the abovementioned objective, logistic regression, classification tree technique, random forest, generalized additive model and maximum entropy were used for modelling. The results were obtained from each model, the differences between the models were compared and discussed statistically and ecologically, and then the most appropriate distribution model was chosen in order to develop the potential distribution map of the species.
MATERIALS AND METHODS – Materijali i metode
Site description – Opis područja
The study site covers Gölhisar, Çavdır, Tefenni and Altınyayla districts in Burdur province, Çameli district in Denizli province, and some parts of Fethiye district in Muğla province. It is located between the east longitudes 35º 44′ 54″ – 35º 19′ 27″ and north latitudes 36º 44′ 03″ – 37º 21′ 33″. The elevation of the site ranges from 540 m to 2300 m. The study site is surrounded by Boncuk mountains in the southwest, Akdağ in the west and Eren Mountains in the south. The site has an area of 252680 hectares with 136743 hectares of forest and 115937 hectares of non-forest area. Crimean juniper, black pine, oak, Brutian pine and Taurus cedar are tree species with the widest distribution. Mediterranean climate is dominant within and around the study site which is located within the boundaries of the Lakes Region. However, since the site is located in the transition zone between the Mediterranean climate and continental climate, features of the transition climate have also been observed. According to the Köppen climate classification, Mediterranean climate (Csa) with mild winters and very hot and dry summers is dominant in the study site (Rubel et al., 2017). According to the Thornthwaite precipitation effectiveness index and climate classification, semi-arid less humid (C1) climate is observed in the site (Yılmaz and Çiçek, 2016). The geological structure of the Gölhisar locality consists of three layers of Lycian, Middle-Upper Miocene and Gölhisar formations in the age range from Mesozoic to the present. These formations contain limestone, sandstone, coarse-grained conglomerate, marl and ophiolitic bedrock types (Elitez et al., 2018; Varol, 2011). Considering the site where the study was conducted, it has poor soil structure since most of the area is located on a sloped and rugged terrain.
Environmental variables –Varijable okoliša
In order to create models and maps through statistical analyses, environmental variables should be created. Aspect, slope, and elevation were created in the raster format using the digital elevation model (DEM) of the Gölhisar district. To determine the landform of the study area, “Topographic Tools” extension was used, and topographic position index map was created (Jennes, 2006). Each bedrock type in the parent materials obtained from the DG of Mineral Research and Exploration was drawn as a polygon considering the boundaries of the study area, and bedrock types were recorded in the attribute table. At the last stage, those bedrock types (limestone, sandstone, chert, serpentine, alluvium, quartzite, basalt) in the form of vectors were exported in raster format using the conversion options. The cellular values of slope and aspect variables created for the study area were used to calculate heat index and radiation index (Equation 1 and 2).
Heat Index = cos(radyan((θ)−θ maks)) x (tan (radyan (∆)))) (1)
Radiation Index = (1 – cos ((π / 180) x (θ – 30))) / 2 (2)
In these equations, θ represents aspect and ∆ represents slope, while θ maks represents 202.5°. The results of equation 1 ranged from -1 to 1 (Parker, 1988; Olsson et al., 2009) and of equation 2 they ranged from 0 to 1 (Roberts and Cooper 1989).
At the final stage, heat index and radiation index variables were created in raster format with “Raster Calculator” tool in ArcMap 10.2 software based on the cellular values of the indices calculated for the entire study area.
Statistical evaluation
At this stage, binary data of Brutian pine were collected from 400 sampling plots each with a size of 20×20 m. Presence-absence data were used for the group discrimination techniques among the correlative approaches, while presence-only data were used for the profile technique. Receiver Operating Characteristic (ROC) curves were created and the accuracy of all models obtained was checked with the Area Under the ROC curve (AUC).
Pearson’s chi square (for categorical variables: limestone, sandstone, chert, serpentine, alluvium, quartzite, basalt) and Mann-Whitney U-tests (for continuous variables: elevation, aspect, slope, topographic position index, heat index, radiation index) were performed to detect whether there was a relationship between Brutian pine and the independent variables (Pearson, 1900; Mann and Whitney, 1947).
Logistic Regression (LR) analysis is a parametric method that predicts the relation between the dependent variable and the independent variable according to the possibility rules. Furthermore, this method is referred to as the logarithmical conversion of the linear regression analysis. Here the dependent variable is categorical and it is applied in three different ways (binary logistic, nominal logistic, ordinal logistic) (Hosmer and Lemeshow, 2000; Şenel and Alatlı, 2014). During the analysis, the dependent variable may be continuous or categorical (Peng et al., 2002; Aksaraylı and Saygın, 2011). The prediction values of the model range from 0 to 1.
Classification and Regression Tree Technique (CART) is called classification tree technique (CTT) if the dependent variable contains binary data, and regression tree technique (RTT) if it contains continuous data. As the presence-absence data of Brutian pine was used in this study, CTT was used. Classification tree is a non-parametric rule-based method and it divides environmental variables into homogenous sub-groups as the dependent variable. These sub-groups form a hierarchical tree model and are connected to one another with leaves and nodes (Breiman et al., 1984; De’ath and Fabricius 2000; Chu et al., 2009; Özkan, 2012b). The independent variable values at the last nodes of the resulting tree model are written with rules, and in this way, the estimated values of the model are obtained (Özkan, 2012b; Özkan, 2013; Mert et al., 2016).
Random Forest (RF), which is a more sophisticated version of CTT, is a non-parametric algorithm-based method. RF produces several classification trees to get the most accurate result and makes assessment by combining the trees it produces. After creating several classification trees, RF combines the predictions from all trees to finalize the process (Cutler et al., 2007; Evans and Cushman, 2009; Grossmann et al., 2010). RF can use categorical, sequenced, and continuous data in the same analysis, and it does not need data conversion (Evans et al., 2011). To create the prediction model, it needs the number of the classification trees and that of the prediction variables on each node. However, the number of the classification trees and the prediction values on each node should be optimized to minimize the generalization error during the analysis (Rodriguez-Galiano et al., 2012). As RF eliminates the overfitting that occurs in CTT method and applies cross validation during the analysis, it is used in many disciplines and has become more popular (Breiman, 2001; Cutler et al., 2007; Grossmann et al., 2010; Evans et al., 2011). In this study, “randomForest” package in R studio software was used for distribution modelling of Brutian pine (Breiman, 2001).
Generalized Additive Model (GAM) is the non-parametric version of the generalized linear modelling technique, and it allows the determination of non-linear distributions with its smoothing function. GAM has a prediction capability in determining the complicated relations between dependent variables and environmental variables. Different assessment functions are used depending on the characteristics of the dependent variable (Guisan et al., 2002; Moisen et al., 2006). In this study, Generalized Regression Analysis and Spatial Prediction (GRASP) in S – Plus 6.1 package software was used to create the species distribution model and map using the GAM technique (Lehmann et al., 2002; Özkan, 2012a; Gülsoy and Özkan, 2013). ANOVA (F test) stepwise model in GRASP was used during the species distribution modelling and mapping process.
Maximum Entropy (MaxEnt) that is one of the methods which uses only presence data in species distribution modelling to create model(s) for the relationships between the dependent variable and environmental variables based on the possibility data in areas with similar features (Phillips et al., 2006; Baldwin, 2009). For the prediction of the model(s) obtained, maximum entropy theory is used. This method, which makes predictions based on incomplete information and determines the possibility distribution, provides the opportunity to assess the categorical and continuous data at the same time (Phillips et al., 2006). On the other hand, MaxEnt can create models using any of the logistic, raw, and logarithmical options. In this study, logistic option was chosen because its possibility values ranged from 0 to 1 and it provided near-real prediction values (Phillips and Dudik, 2008; Baldwin, 2009). While predicting the presence possibility, 0 gets the lowest prediction value while 1 gets the highest value (Phillips et al., 2004; Kumar and Stohlgren, 2009).
RESULTS – Rezultati
Mann-Whitney U-test results show that elevation, slope, topographic position index, and heat index are significant for the occurrences of Brutian pine (Table 1). According to the result of Pearson’s chi-squared test, limestone, sandstone, chert, and serpentine were detected playing an important role in the site properties factors of Brutian pine (Table 2). Environmental variables which are considerably related to the independent variables according to the results of Mann-Whitney U-test and Pearson’s chi-squared tests were involved in the modelling processes.
Table 1. Mann-Whitney U-test results for continuous variables
Tablica 1. Rezultati Mann-Whitney U-testa kontinuiranih varijabli
Table 2. Pearson’s chi-square (𝔁2) test results for continuous variables
Tablica 2. Rezulati Pearsonova hi-kvadrat (𝔁2) testa kontinuiranih varijabli
In the model obtained from LR analysis, sandstone, which was a bedrock type, and elevation were found to be the important variables. In the analysis, backward LR method was used and the adequacy of the fit between the variables that composed the models was checked with Hosmer-Lemeshow test. The significance of the model according to Hosmer-Lemeshow test was found to be 0.146 (p>0.05). This value shows that the model is valid. Elevation provided the highest contribution to the model. Both variables in the model had a negative correlation. In other words, as elevation increased, the species distribution decreased and preferred the areas without sandstone. The validity of the model was checked with the AUC, while the values were found to be 0.882 for the training dataset and 0.881 for the test dataset. The probability value of the model obtained from the LR analysis was calculated using the Equation 3 below.
(3)
Sandstone as one of the bedrock types and elevation were the variables that constructed the tree model obtained from CTT. The tree model comprised 6 groups and 4 terminal nodes. Elevation provided the highest contribution to the model. According to the tree model, areas below 1345 m and areas with sandstone between 1345–1400 m represented the potential distribution areas of the Brutian pine (Figure 1). The AUC values of the training dataset and the test dataset of the model were found to be 0.927 and 0.913, respectively.
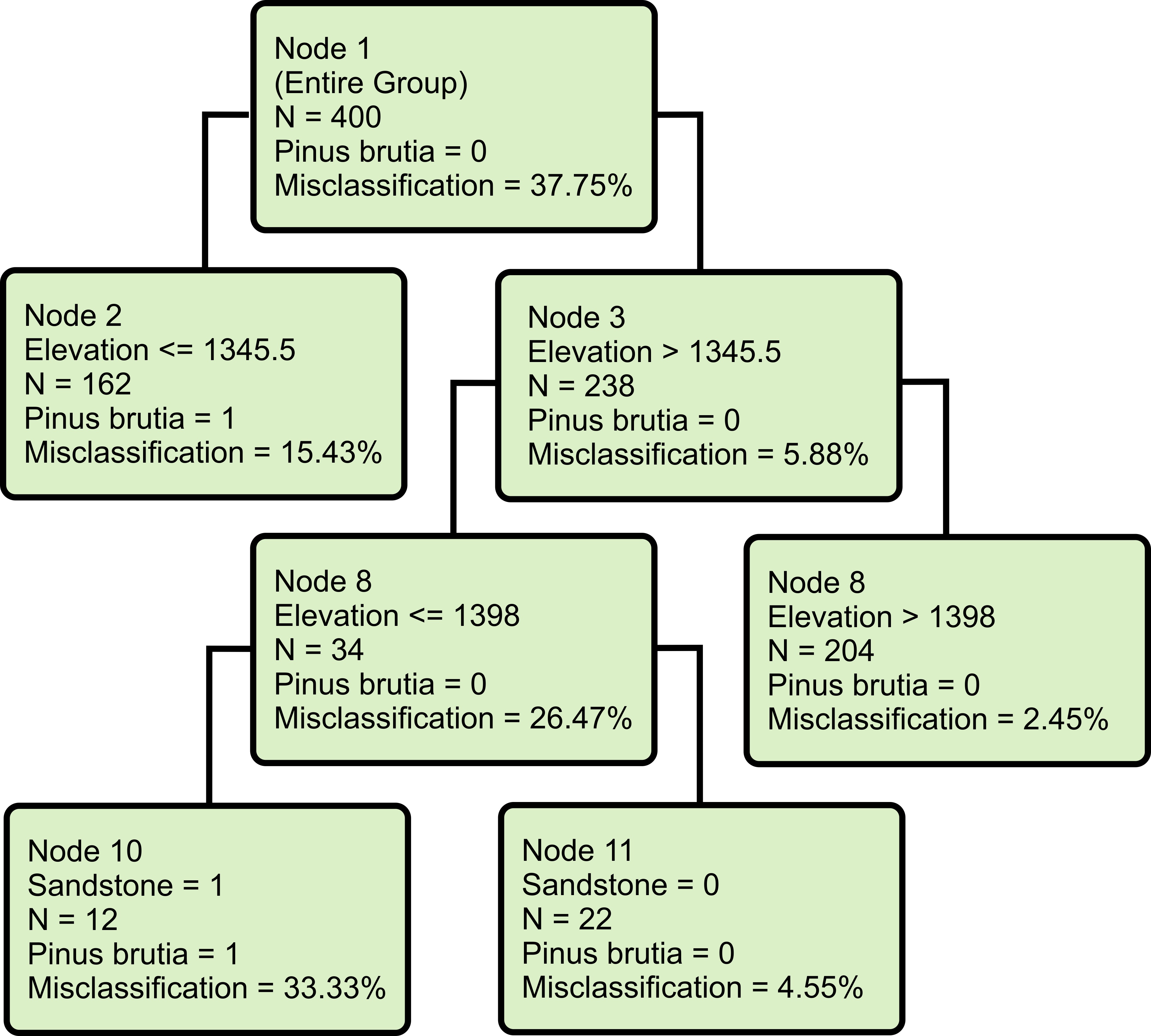
Figure 1. Tree model of the Brutian pine
Slika 1. Model stabla brucijskog bora
The number of the most ideal decision trees in the model created with the RF method was selected as 500 as reported by Breiman (2001). The variables constructing the model included elevation, heat index, topographic position index and bedrock types. Regarding the contribution of the variables in accordance with the Gini value, elevation (109.17), heat index (17.26), topographic position index (15.39) and bedrock types (sandstone (12.43), chert (2.12), limestone (1.93), serpentine (1.23)) had the highest contribution (Figure 2). According to the constructed random forest model, Brutian pine showed potential distribution up to 1600 m altitude, hot or hotter aspects, plains, open slopes, and convex lands and sandstone areas. On the other hand, the AUC value of the model was found to be 0.938.
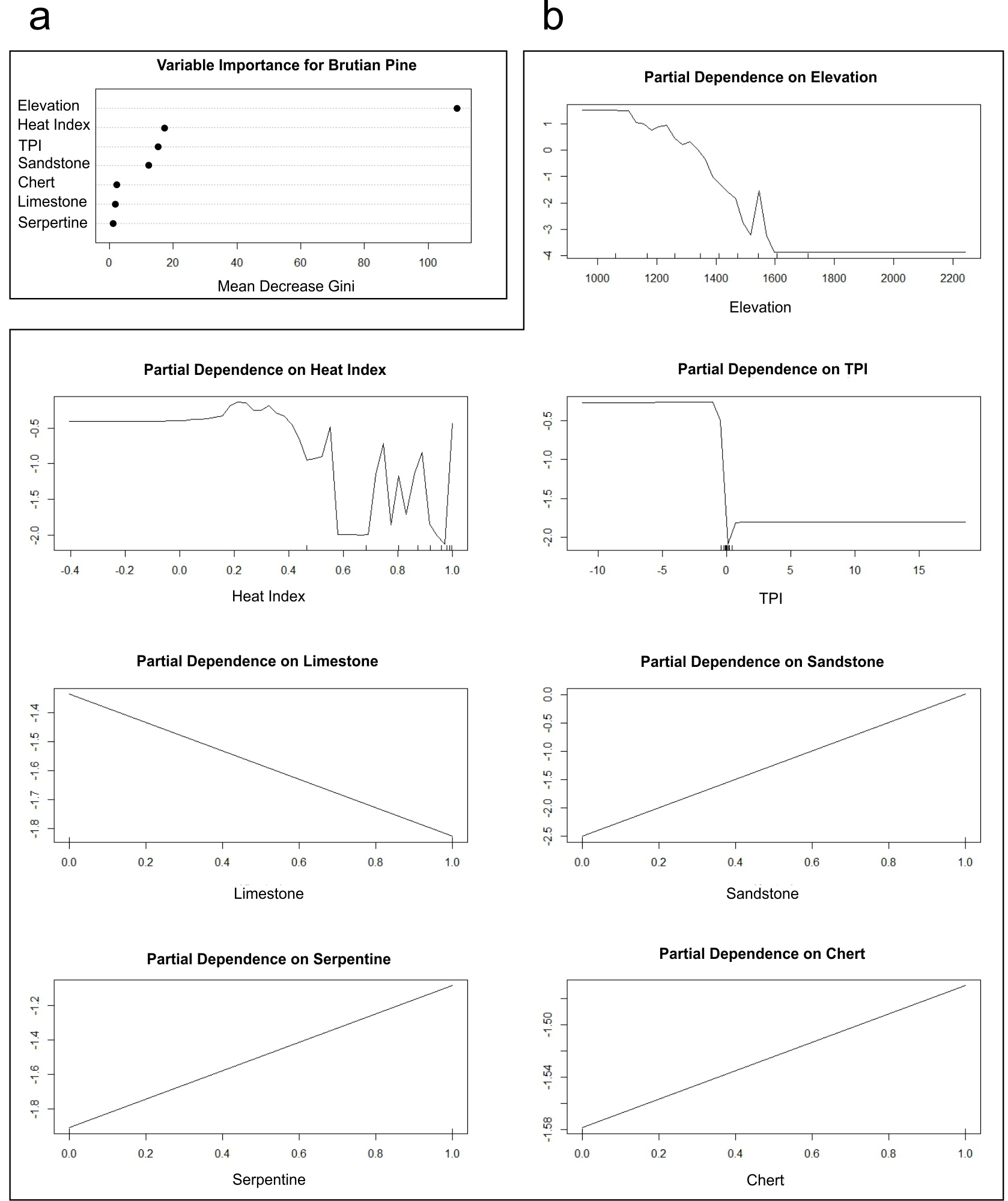
Figure 2. Random forest variable importance (a) and model results of response curves (b) of environmental variables for Brutian pine
Slika 2. Značajnost varijable prema modelu slučajne šume (a) i rezultati modela krivulja odgovora (b) varijabli okoliša za brucijski bor
Elevation, bedrock types and heat index were the variables used in the GAM, and among them elevation had the highest contribution. According to the model, elevations of 950–1500 m were the most suitable potential distribution areas for Brutian pine, while the distribution of the species decreased gradually starting from the elevation of 1600 m. Heat index, which was another variable in the model, showed that hot and hotter aspects created appropriate areas for the species, while as the index value got closer to 1, its distribution gradually increased. Finally, areas with sandstone constituted the most suitable potential distribution areas for Brutian pine (Figure 3). The formula of the model was = s (Elevation, 4) + Bedrock Types + s (Heat Index, 4). The validation value of the model was 0.964, while the cross validation result was 0.937.
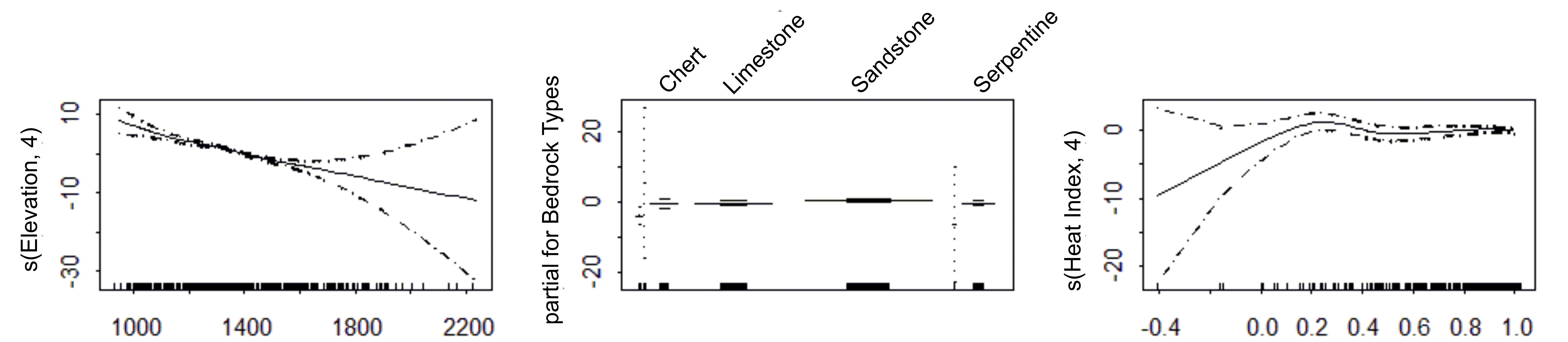
Figure 3. Response curves of environmental variables in the GAM analysis
Slika 3. Krivulje odgovora varijabli okoliša u GAM analizi
According to the MaxEnt results related to P. brutia, elevation, heat index, topographic position index, and bedrock types were the variables used for constructing the model. Elevation and bedrock types had the highest impact in the model. The distribution of Brutian pine increased up to the elevation of around 1100 m, while its distribution decreased as the elevation increased. The distribution of Brutian pine in the area was found to be related to sandstone, serpentine, limestone, and chert among bedrock types. Hot and hotter aspects were found to be the most suitable potential distribution areas. Finally, the species was found to have a potential distribution area on plains, open slopes, and convex lands such as hills and summits according to the topographic position index (Figure 4). The AUC values of the model were 0.854 for the training dataset and 0.803 for the test dataset.
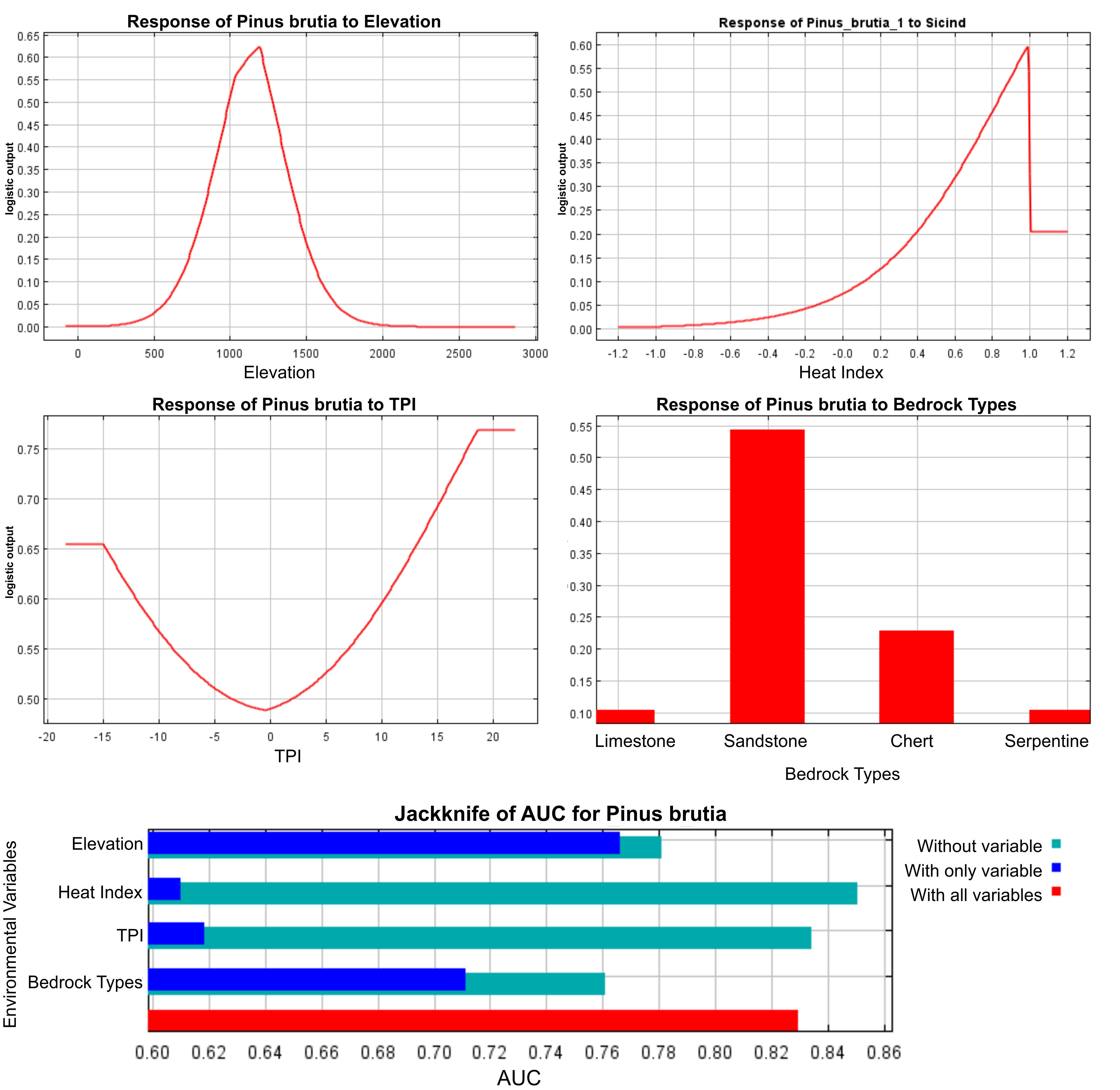
Figure 4. Response curves and results of jackknife estimation of relative importance of environmental variables for Brutian pine
Slika 4. Krivulje odgovora i rezultati jackknife procjene relativnog značaja varijabli okoliša za brucijski bor
The model with the highest AUC value according to the correlative approaches was obtained from the GAM technique. Potential distribution maps were created based on the distribution model obtained from the GAM technique and visualized using ArcMap 10.2 software (Figure 5).
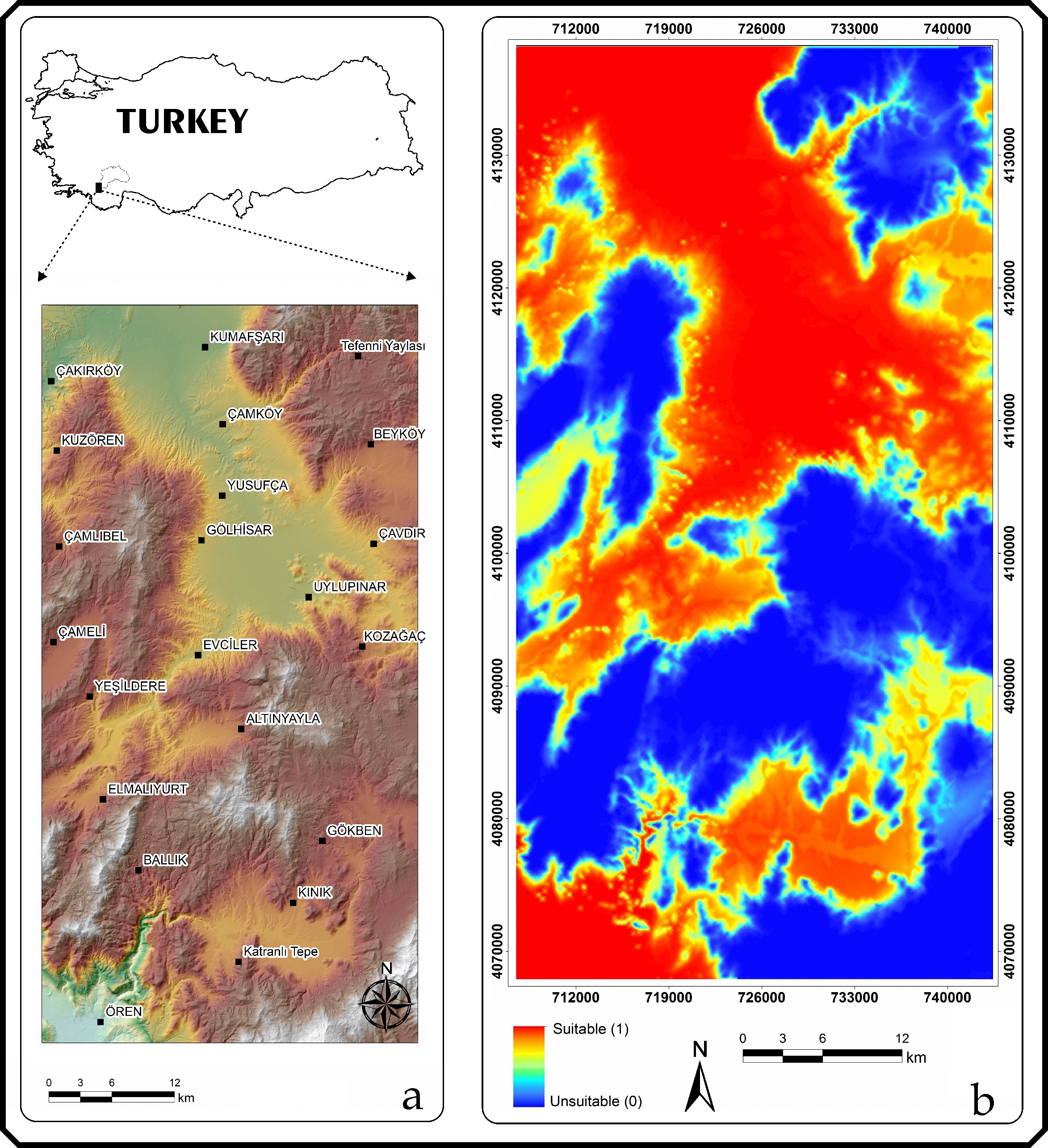
Figure 5. a) Location map of the study area; b) Species distribution model maps of GAM
Slika 5. a) Karta lokacije područja istraživanja; b) Karte distribucije vrste prema modelu GAM
DISCUSSION – Rasprava
In this study, which was conducted using five different modelling techniques, potential distribution models and maps were created for Brutian pine distribution in the Gölhisar district. The differences between the models were compared and the most appropriate distribution model’s map was visualized. The models obtained with each method were constructed by elevation, bedrock types, heat index, topographic position index, and slope. Furthermore, elevation and bedrock types had the highest contribution to the models. The accuracy of the models was checked with AUC. The highest performance was found in GAM, RF, CTT, MaxEnt and LR methods, respectively.
Brutian pine, which is mainly distributed in the Mediterranean and Aegean regions in Türkiye, is locally distributed in the inlands of the Central and Western Black Sea region (Arbez, 1974; Kandemir et al., 2010; Şentürk et al., 2019). Brutian pine establishes pure stands up to the elevation of 800 m in the Mediterranean and Aegean regions where it has its primary distribution, whereas it also establishes mixed stands with other main forest tree species up to the elevation of 1200 m. It is distributed up to 1600 m in the Gölhisar district (Kılıç and Güner, 2000), while the models created revealed that the most suitable distribution areas were located up to the elevation of 1400–1500 m. In most parts of the Taurus Mountains which are karstic, Brutian pine develops well. Brutian pine grows on such bedrock types as primarily limestone and marl, conglomerate, serpentine, basalt sandstone and schist (Atalay et al., 2008; Atalay and Efe, 2015). It mainly prefers areas with sandstone and limestone in that locality, while it avoids areas with alluvium. Elevation and bedrock types constructed all the models in the study. In the study, Brutian pine was found to prefer sunny aspects, which is because it is a light-demanding tree species. At sufficient light concentrations, it develops better. On the other hand, open slopes and midslope lands, and convex lands such as hills and summits were the appropriate distribution areas for Brutian pine by topographic position index. Slope areas plays an important role in the growth of Brutian pine stands (Atalay et al., 2008). Some studies found that the productivity of Brutian pine stands increased as the slope increased depending on elevation (Özkan and Kuzugüdenli, 2010). In a study conducted in the same district, midslope was found to be one of the important factors for the distribution of Brutian pine (Şentürk, 2012).
The model from the LR analysis was constructed by elevation and sandstone and AUC values of these variables were found to be 0.882 and 0.881. LR had the lowest AUC value compared to the other methods used in the study. The reason is that LR analysis is a non-linear method and thus it can hardly classify the variables (Holden et al., 2011). As known, relationships in forest ecosystems are usually complex; therefore, non-parametric methods provide more accurate results to determine these relationships (Özkan, 2012b; Özkan, 2013).
CTT and RF are rule-based non-parametric methods and construct the models by assessing the best options in modelling (Holden et al., 2011). There are differences between CTT and RF. RF creates decision trees without a need for pruning, and validates the model’s performance. While creating each decision tree without requiring the training and test sets, it can determine the relationships and distance between the variables composing the model and eliminate the overfitting; which makes it superior to the classification tree technique (Breiman, 2001; Grossman et al., 2010; Özdemir, 2018). However, the tree model and the process steps are not visible entirely (black box), which is a disadvantage of the RF technique (Breiman, 2001; Cutler et al., 2007; Evans et al., 2011).
In this study, MaxEnt technique had a lower performance compared to the other non-parametric methods. Brutian pine, which was selected as the target species, is distributed widely in the Gölhisar locality due to its high ecological tolerance range. The most important difference of MaxEnt from other techniques is that it creates species distribution models using presence-only data. This method produces absence data artificially using the cell values in the background and creates the distribution model by calculating the possibilities based on these cells (Phillips et al., 2006). In particular, it provides better results when creating habitat suitability models in wildlife studies, when determining the distribution areas of endemic or rare, endangered species, and identifying the present and future impacts of climate change on the distribution of species (Ray et al., 2011; Babar et al., 2012; Clements et al., 2012; Kumar, 2012; Marcer et al., 2013; Garcia et al., 2013; Ma et al., 2014; Kıraç and Mert, 2019; Süel, 2019; Acarer, 2024). Since it is difficult to validate the absence data of the target species in habitat suitability modelling studies (Mateo et al., 2010), presence-only data is suitable for such studies. On the other hand, the use of presence-absence data is more suitable in developing the distribution models of plant species. However, if the plant species is distributed in a narrow area, rare or endemic, MaxEnt can be effective. Moreover, MaxEnt provides more effective results in case the number of sampling plots is low, which is why it is preferred in some studies (Phillips et al. 2004; Elith et al., 2006; Hernandez et al., 2006; Pearson et al., 2007; Wisz et al., 2008; Kumar and Stohlgren, 2009).
In this study, the most successful model was obtained by the GAM technique. Compared to the methods commonly used in species distribution modelling studies, GAM technique has a specific smoothing function which ensures both fitting between the environmental changes and explanatory curves (Lehmann et al., 2002) and more accurate ecological interpretation of the models (Austin, 1999; 2002). Since the relationships in ecosystems are complicated, this function of the GAM technique to explain the curvilinear relationships ensures fitting between the dependent variable and environmental variables and thus improves the prediction capability of the model (Yee and Mitchell 1991).
CONCLUSIONS – Zaključci
Increasing the number of variables in the modelling techniques is as important as the use of different modelling techniques to improve the prediction capability of the target species (Moisen and Frescino, 2002). On the other hand, the adequacy of the sampling conducted for the target species (number of sample areas, type of data, ability to represent the species in the district, etc.) is also important in increasing the success of modelling techniques. In this study, the results of different models were significantly similar. However, the results of the correlative approaches were better than those of the MaxEnt method which is a profile technique. This is due to the reliability of the inventory data of the species (presence-absence data) (Elith et al., 2006; Phillips and Dudik, 2008). According to the GAM technique that had the best result; elevations from 950 m to 1500 m, hot and hotter aspects and areas with sandstone represented the most suitable potential distribution areas. This distribution map provides basic information that plays a crucial role in the decision-making process for the planning of Brutian pine species. It is also important to create the potential distribution maps of the other target species in the region using similar techniques for a holistic ecosystem planning. It should be noted that each technique has its unique advantages. It is important to consider various factors, such as data types of the target species, the number of sample areas, and explanatory variable selection, when selecting the most suitable modelling technique.
