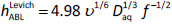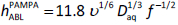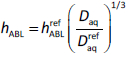In permeability assays using microtitre plates, either based on cellular models (e.g., Caco-2, MDCK) or PAMPA (parallel artificial membrane permeability assay) [1-3], the thickness of the aqueous boundary layer (ABL) has been approximated by:
where Daq is the diffusivity, f is the stirring frequency (RPM), and K and α are fitted constants [4-9].
Based on testosterone Caco-2 measurements, Karlsson and Artursson [5] reported α = 1 and implied K = 0.57 x 10-6 cm/s. Adson et al. [6] reported K = 4.1 x 10-6 cm/s and α = 0.8, also for testosterone. Orbital shakers were used to agitate the microtitre plates during the assay, as is the common practice in cellular assays. Both groups noted that the K parameter is a function of aqueous diffusivity, kinematic viscosity, and geometrical factors. Adson et al. [6] pondered on the α factor being greater than the theoretically expected value of 0.5 and reasoned that the asymmetric hydrodynamic conditions of the Transwell plates may have led to the elevated values.
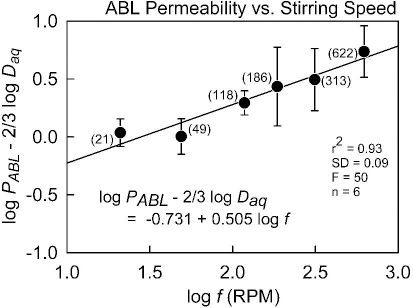
In a PAMPA study of 53 ionizable molecules, Avdeef et al. [9] determined the ABL permeability, PABL, using the pKaflux method at four different stirring speeds (49, 118, 186, 622 RPM). Efficient individual-well magnetic stirring (using the Gut-Box device) was used in their study. Since PABL = Daq / hABL, the constants K and α can be determined for each molecule by linear regression based on log PABL = log K + α log f. The pKaflux method uniquely made such an analysis possible. The least-squares refined parameters (based on several molecules) were reported as K = 23.1 x 10-6 cm/s and α = 0.709. The implicit assumption in the analysis was that for a given rate of stirring, there is a unique ABL thickness for all molecules.
In the above three studies, different values of α were reported, all greater than the theoretical value of 0.5 expected from the solution to the convective diffusion model partial differential equation, based on the rotating disk geometry, according to Levich [10]. In the theoretical model, the thickness of the ABL may be calculated from:
where ν is the kinematic viscosity (cm2/s). If the Levich equation were applicable to microtitre plate permeability assay geometries, thenEq. (2) suggests that K = 0.201 ν- 1/6 Daq2/3, provided α were 0.5 inEq. (1). Hence, each molecule in the permeability assay would be expected to have its own hABL value, depending on its diffusivity. According to Pohl et al. [11], such "theoretical predictions ...[are]... widely ignored." Moreover, using ion-selective microelectrodes, Pohl and coworkers unequivocally showed that hABL varied with ionic substances at a given level of stirring.
In this Communication, it is hypothesized that the theoretical α = 0.5 was obscured in prior Caco-2 and PAMPA microtitre plate permeability studies [5-9], either because (i) K was evaluated without explicit consideration of the Daq term from the Levich equation, and/or (ii) the data were not of sufficient sensitivity to reveal the theoretical values. We proceeded to test the hypothesis with PAMPA data by re-arranging the Levich equation into a parametric form. Combining PABL = Daq / hABL withEq. (2) and converting into the logarithmic form:
with the theoretical constants a = log (0.201 w-1/6) = -0.356 (25 °C) and b = 0.5. We appliedEq. (3) to the (PABL, f) data of Avdeef et al. [9], augmented with additional measurements at 21 and 313 RPM (Table 1), and found a = -0.731 and b = 0.505 (r2 = 0.93, SD = 0.09, F = 50, n = 6). The plot of the data used in the re-analysis is shown inFigure 1. The slope factor, 0.505, is so close to the theoretical value that we propose to simply use the theoretical value henceforth. Substituting the new parameters intoEq. (3) and converting the resulting equation to the form ofEq. (2) results in:
FromEqs. (2) and(4), hABLPAMPA/hABLLevich = 2.4. The geometry of the rotating disk apparatus allows the convective flow to reach closer to the rotating surface (thus diminishing the thickness of the pure diffusion layer) compared to the geometry of magnetically stirred PAMPA wells. The stirring of Caco-2 plates by orbital shakers produces even a greater ratio, hABLCaco-2/hABLLevich, indicating less "efficient" stirring [9].Table 2 shows sample calculations usingEqs. (2) and(4) for three drugs, widely ranging in size.
Pohl et al. [11] suggested that if a single reference compound is used to calibrate the geometrical factor, then calculations of subsequent hABL should be according to the diffusivity dependence in the Levich equation:
Eq. (5) was experimentally verified with several combinations of ions and buffers by Pohl et al. [11], using pH and other ion-selective microelectrodes to directly measure the change in concentrations in the aqueous boundary layer adjacent to black lipid membranes.
In conclusion, the stirring frequency exponent of -1/2 in the theoretical Levich expression appears to apply to PAMPA assays, where efficient individual-well magnetic stirring (> 20 RPM) is used. The same may be true for Caco-2 assays, although additional measurements at varied stirring speeds would make this a more confident assertion. If a single molecule is used as a stirring calibrant, then it seems reasonable to use the scaling suggested byEq. (5) with microtitre plate data. AsTable 2 suggests, the error in calculating hABL based on unscaled hABLref can be as high as 30 %. Hence, it is prudent to incorporateEq. (5) in the calibration procedure. This is especially important to bear in mind for nonionizable molecules since the pKaflux method cannot be directly applied to them. This is of practical importance in PAMPA and perhaps cellular assays as well.