The Influence of the Eccentric Thrust Force on the Selection of a Stern Tube Slide Bearing

2.1. Eccentric thrust force / Ekscentrična porivna sila

The resulting thrust force F_T (hereafter referred to as "thrust force") with the position outside the center of the propeller is called the eccentric thrust force. It is obtained as the concentrated force by integrating the pressure field over the surface of the propeller and then dividing by its surface.

The Croatian Register of Shipping for the review calculations of the ship's propulsion shafting systems supposes that the thrust force F_T is calculated to act perpendicular to the y- z plane of the propeller in a direction parallel to the x-axis of the shaft, and that its position is above the y-axis at the distance e_T from the propeller center in amount of 4% of the propeller outer diameter D [4].

However, from what was said in the introduction, taking into account the variable velocity field on the ship's propeller, it follows that the position of the thrust force F_T is variable and cannot be determined in advance, i.e. it can be anywhere on the surface of the propeller (Figure 1).

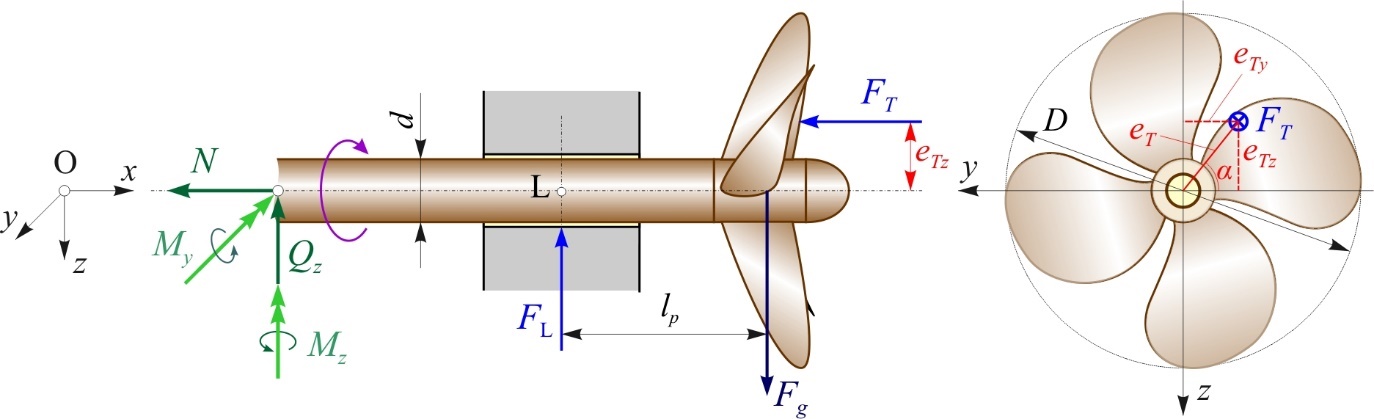
Figure 1 Theoretical load model of the stern tube slide bearing

Slika 1. Teoretski model opterećenja statvenog kliznog ležaja

In addition to the bending moment with respect to the point L generated by the weight of the propeller F_g (the self-weight of the shaft is neglected), there are also moments generated by the action of the thrust force F_T with respect to its position, i.e.:

- moment about the y-axis, M_Ly :

[TeX:] M_{\text{Ly}} = F_{g} \bullet l_{p} \pm F_{T} \bullet e_{\text{Tz}}\ $M_{\mathrm{\text{Ly}}}=F_g\bullet l_p\pm F_T\bullet e_{\mathrm{\text{Tz}}}$ (Nm) and (1)

- moment about the z-axis, M_Lz :

[TeX:] M_{\text{Lz}} = \pm F_{T} \bullet e_{\text{Ty}}\ $M_{\mathrm{\text{Lz}}}=\pm F_T\bullet e_{\mathrm{\text{Ty}}}$ (Nm), (2)

where:

l_p - length between propeller and stern tube slide bearing (m),

e_Tz and e_Ty - projections of the distance e_T onto the z and y axes (m).

These moments M_Ly and M_Lz correspond to the spatial elasticity line of the shaft sleeve inside the stern tube bearing.

In the remainder of the paper, for the sake of simpler analysis, it was assumed that the positon of the thrust force F_T is on the negative axis z for the case of straight ahead and astern navigation, and on the positive axis y for the case of turning of the ship. The amount of the distance e_T according to the rule-of-thumb used by the Croatian Register of Shipping is assumed, i.e. e_Tz = e_Ty = e_T = 4% D.

In this case, for further analysis, the moment of the eccentric thrust force is M_P :

[TeX:] M_{p} = \pm F_{T} \bullet e_{\text{Tz}} = \pm F_{T} \bullet e_{\text{Ty}} = \pm F_{T} \bullet e_{T}\ $M_p=\pm F_T\bullet e_{\mathrm{\text{Tz}}}=\pm F_T\bullet e_{\mathrm{\text{Ty}}}=\pm F_T\bullet e_T$(Nm). (3)

2.2. Calculation of the thrust force / Proračun porivne sile

The thrust force F_T produced by the propeller can be determined from the expression [5]:

[TeX:] F_{T} = \frac{P_{D}}{V_{a}} \bullet \eta_{o}$F_T=\frac{P_D}{V_a}\bullet {\eta }_o$ (N), (4)

where:

P_D - power delivered to propeller (kW),

v_a - advance speed (m/s),

η_o - open water propeller efficiency.

Power delivered to propeller P_D can be determined from the expression [5]:

[TeX:] P_{D} = P_{B} \bullet \eta_{s}$P_D=P_B\bullet {\eta }_s$ (kW), (5)

where:

P_B - rated power of the main engine (kW),

η_s - shaft efficiency, which is:

0.95-0.98 for long shafts and if a reduction gear is installed.

Advance speed v_a can be determined from the expression [5]:

[TeX:] v_{a} = v \bullet \left( 1 - w \right)$v_a=v\bullet (1-w)$ (m/s), (6)

where:

v - ship speed (m/s),

w - wake fraction coefficient, which is:

0.2-0.45 for the propeller arrangement as a single screw.

To calculate the geometric and hydrodynamic characteristics of the fixed pitch propellers, the Wageningen B series propellers are extensively used [6,7,8]. From typical propeller design diagram B_P - δ it is possible to select values of the optimal open water propeller efficiency η_o and pitch ratio H/ D [8].

The design coefficient B_p is defined as [8]:

[TeX:] B_{P} = 0.220 \bullet \frac{n \bullet \sqrt{P_{D}}}{V_{a}^{2.5}}$B_P=0.220\bullet \frac{n\bullet \sqrt{P_D}}{V_a^{2.5}}$, (7)

while for the selected propeller diameter D, the design coefficient δ is defined as follows [8]:

[TeX:] \delta = 1.688 \bullet \frac{n \bullet D}{V_{a}}$\delta =1.688\bullet \frac{n\bullet D}{V_a}$. (8)

The expressions for the design coefficients (7) and (8) are adapted to the measurement units for: n - rated rotation speed of the propeller (in rpm), P_D - power delivered to propeller (in kW), v_a - advance speed (in m/s) and D - propeller diameter (in m).

Values for the δ are reduced by 4-6% for the propeller arrangement as a single screw [7].

The magnitude of the thrust force F_T can be controlled using the expression given by the Croatian Register of Shipping [9]:

[TeX:] F_{T} = 57.6 \bullet 10^{6} \bullet \frac{P}{H \bullet n}$F_T=57.6\bullet {10}^6\bullet \frac{P}{H\bullet n}$ (N), (9)

where:

P - rated power P = P_B (kW),

H - mean propeller pitch (mm),

n - rated rotation speed of the propeller (rpm).

2.3. Simplified analytical model of the shaft line / Pojednostavljen analitički model vratilnog voda

The aim of the paper is to study justifiable engineering methods to facilitate the selection of the stern tube bearing, i.e. to create analytical models of shaft lines that allow the correct selection of the type of stern tube slide bearing. Therefore, it is necessary to find the suitable analytical model and eventually simplified expressions that can be used in the initial stage of stern tube bearing selection. In this way, the recommendation for the selection of the stern tube bearing could be made in a simplified way.

Figures 2 and 3 show the general models of shaft lines of ship propulsion systems with six (ABCDELP), five (ABDELP) and four (ADELP) supports, loaded by the weight of the propeller F_g and the moment of eccentric thrust force M_P , which are analytically closest to the real models. The models are with one stern tube slide bearing, i.e. with the aft stern tube slide bearing [10,11]. Point P marks the position of the propeller, support L represents the aft stern tube slide bearing, support A represents the fore bearing of the prime mover (e.g. marine Diesel engine), while the other supports are radial support bearings of the intermediate shaft(s). The aim is to simplify the general model and limit it to two fields of the intermediate shaft of the shaft line towards the propeller in order to facilitate future calculations and analyses. To confirm the above, the simplified model is compared with the general model.

Figure 2 General model of the shaft line loading by the weight of the propeller F_g

Slika 2. Opći model vratilnog voda za slučaj opterećenja težinom brodskog vijka F_g

Figure 3 General model of the shaft line loading by the moment of eccentric thrust force M_P

Slika 3. Opći model vratilnog voda za slučaj opterećenja momentom ekscentrične porivne sile M_P

For the general model, an analysis of the influence of the number of supports (i.e. intermediate shafts) on the deflection of the shaft at the location of the propeller w_P and on the slope of the elastic line of the shaft sleeve in the stern tube bearing β_L was performed using the method of initial parameters (transfer matrix) [12]. The analysis covers the lengths of propeller shafts of the ship propulsion shaft lines determined by the expression according to the rules of the Croatian Register of Shipping [9]:

[TeX:] 5.5\sqrt{d} \leq l \leq \lambda\sqrt{d}\ $5.5\sqrt{d}\le l\le \lambda \sqrt{d}$(m), (10)

where:

l - length of propeller shaft (length between the two aftmost bearings E and L) (m),

d - calculated diameter of the intermediate shaft (m),

λ - value of the factor, which is:

= 14 for n ≤ 500 rpm

= [TeX:] \frac{300}{\sqrt{n}}$\frac{300}{\sqrt{n}}$ for n ≥ 500 rpm,

n - rated rotation speed of the propeller shaft (rpm).

According to the expression (10) for n ≤ 500 rpm and d ≤ 300 mm, the length between the two aftmost shafting bearings is: 3.012 ≤ l ≤ 7.668 m. In the paper, the calculation of the shaft deflection at the location of the propeller w_P and the slope of the elastic line of the shaft sleeve in the stern tube bearing β_L is given for equal amounts of the intermediate shaft length l₁ = l of 3, 5 and 7 m [12]. The results obtained were compared with those obtained for the simplified models shown in Figures 4 and 5. The values from Section 3 were used for this calculation.

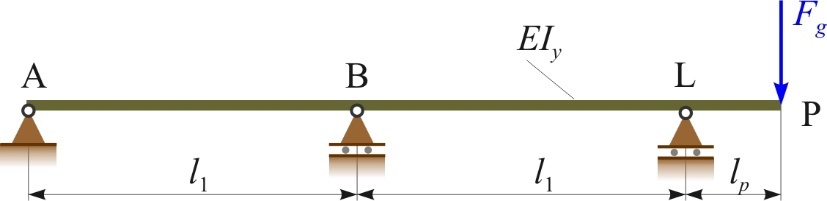
Figure 4 Simplified model of the shaft line loading by the weight of the propeller F_g

Slika 4. Pojednostavljen model vratilnog voda za slučaj opterećenja težinom brodskog vijka F_g

Figure 5 Simplified model of the shaft line loading by the moment of eccentric thrust force M_P

Slika 5. Pojednostavljen model vratilnog voda za slučaj opterećenja momentom ekscentrične porivne sile M_P

Tables 1 and 2 show the deviations of the shaft deflection at the location of the propeller and the slope of the elastic line of the shaft sleeve in the stern tube bearing of the simplified model in comparison with the general model (ABCDELP, ABDELP and ADELP) in the cases of loading by the weight of the propeller F_g and the moment of the eccentric thrust force M_P . In the same tables, the results for the deflection of the shaft at the location of the propeller w_Ps and the slope of the elastic line of the shaft sleeve in the stern tube bearing β_Ls of the simplified model are given.

Table 1 Deviations of deflection and slope in the case of loading by the weight of the propeller F_g

Tablica 1. Odstupanja progiba i nagiba za slučaj opterećenja težinom brodskog vijka F_g

Table 2 Deviations of deflection and slope in the case of loading by the moment of the eccentric thrust force M_P

Tablica 2. Odstupanja progiba i nagiba za slučaj opterećenja momentom ekscentrične porivne sile M_P

Tables 1 and 2 show that the results for the deflection w_Ps and the slope β_Ls of the simplified model do not differ by more than 1% compared to the general model. Therefore, for further analysis of the influence of the external load (the weight of the propeller F_g and the moment of the eccentric thrust force M_P ) on the elastic line of the shaft sleeve, the part of the shaft line towards the direction of the propeller is considered, exactly as shown in Figures 4 and 5. The rest of the shaft line in the direction of the ship's engine has no significant influence on the shape of the elastic line of the shaft sleeve in the stern tube bearing.

2.4. Deflection of the stern tube bearing sleeve / Progib rukavca statvenog ležaja

For the schematic representation of the elastic line of the shaft sleeve through the stern tube slide bearing with the relevant parameters, see Figure 6.

Figure 6 Elastic line of the shaft sleeve through the stern tube bearing

Slika 6. Elastična linija rukavca vratila kroz statveni ležaj

For the simplified model, an analysis of the deflection of the shaft sleeve in the stern tube bearing was carried out for different constructive characteristics of the bearing L/ D and the length of the intermediate shaft l₁. The results of the deflection of the shaft sleeve in the forward w_Af and aft w_Aa ends of the aft stern tube bearing, and the difference in the deflection of the shaft sleeve at the edges of the stern tube bearing Δ w_L for the cases of loading of the shaft line by the weight of the propeller F_g and the moment of the eccentric thrust force M_P can be obtained using the method of initial parameters [12].

From Figure 6 it can be concluded that the difference in the deflection of the shaft sleeve at the edges of the stern tube bearing Δ w_L is equal to the product of the slope of the elastic line in the stern tube bearing β_L and the length of the bearing itself L:

[TeX:] \mathrm{\Delta}W_{L,approx} = \beta_{L\ } \bullet L$\Delta W_{L,approx}={\beta }_L\bullet L$ (mm), (11)

where:

β_L - slope of the elastic line (rad).

The analysis resulted in an expression for calculating the deflection difference Δ w_L,approx :

- in the case of loading by the weight of the propeller F_g :

[TeX:] \mathrm{\Delta}w_{L,approx} = \frac{7}{24} \bullet \frac{F_{g} \bullet l_{p} \bullet l_{1}}{E \bullet l_{y}}L$\Delta w_{L,approx}=\frac{7}{24}\bullet \frac{F_g\bullet l_p\bullet l_1}{E\bullet l_y}L$ (mm), (12)

- in the case of loading by the moment of the eccentric thrust force M_P :

[TeX:] \mathrm{\Delta}w_{L,approx} = \frac{7}{24} \bullet \frac{M_{p} \bullet l_{1}}{E \bullet l_{y}} \bullet L$\Delta w_{L,approx}=\frac{7}{24}\bullet \frac{M_p\bullet l_1}{E\bullet l_y}\bullet L$ (mm) (13)

where:

F_g - propeller weight (N),

M_P - moment of the eccentric thrust force (Nm),

E ∙ I_y - bending stiffness of the shaft (Nm²),

l_p - length between the propeller and the stern tube bearing (m),

l₁ - intermediate shaft length (m),

L - stern tube bearing length (mm).

Comparing the results obtained by the method of initial parameters and expressions (12) and (13), it can be concluded that the mentioned expressions can be used in the initial stage of the stern tube bearing selection for models of ship propulsion systems shaft lines with one (aft) stern tube bearing and with approximately equal lengths of intermediate shaft l₁.

From them, the deflection values in the forward w_Af and aft w_Aa ends of the stern tube bearing can be derived, assuming that:

[TeX:] w_{\text{Af}} = w_{\text{Aa}} \approx \pm \frac{\mathrm{\Delta}w_{L,approx}}{2}$w_{\mathrm{\text{Af}}}=w_{\mathrm{\text{Aa}}}\approx \pm \frac{\Delta w_{L,approx}}{2}$ (mm). (14)

The given methodology does not consider the influence of vibrations, but still enables an initial good selection of stern tube slide bearings, considering the impact of loads due to different navigation regimes on the wear of the bearing bush material and leakage of lubricant, which represents an environmental problem [13,14]. The analysis of the deflection values obtained by this methodology and their comparison with the expected minimum lubricant thickness h₀ opens up the possibility of more correct selection of the stern tube bearing tribosystem in the initial stage. The aim is to ensure proper operation and energy efficiency of the shaft line (minimising frictional losses) and environmental acceptability (minimising lubricant leakage with particles of bearing bush material). The stern tube slide bearing selected this way should ensure optimal performance, long-term reliability and economic justification.

2.4. Procedure for the initial selection of the stern tube bearing / Procedura za početni odabir statvenog ležaja

The presented methodology is summarized with the procedure for the initial selection of the stern tube bearing. The input parameters required for this procedure are given in Table 3, while Table 4 contains expressions that must be followed for this purpose.

Table 3 Input parameters

Tablica 3. Ulazni parametri

Table 4 Output parameters

Tablica 4. Izlazni parametri

3.1. Calculation of the moment of the eccentric thrust force / Proračun momenta ekscentrične porivne sile

In this section the real example was used in further analysis. The ship is powered by a slow-speed Wärtsilä marine Diesel engine RT-flex35 with the maximal continuous rated power of P_B = 3475 kW at the rotation speed of n_e = 167 rpm [4]. The chosen diameter of the propeller shaft is d = 300 mm, so the diameter of the bearing is D = 300 mm. The modulus of elasticity of the shaft is E = 200 GPa, so its bending stiffness is E ∙ I_y = 79.522∙10⁶ N/m². The diameter of the propeller is D = 4 m, its weight is F_g = 100 kN, and it acts on the arm l_P = 0.5 m with respect to the point L (Figure 1).

Power delivered to propeller if η_S = 0.95 according to expression (5) is P_D = 3301.25 kW. Rated rotation speed of the propeller shaft (propeller) is n = 167 rpm (transmission ratio i = 1). Advance speed for the ship speed of v = 15 knots (7.717 m/s) and the wake fraction coefficient w = 0.2 according to expression (6) is v_a = 6.174 m/s.

For this analysis, the four blade fixed pitch propeller type B, series B.4.55. is selected [7]. According to expressions (7) and (8), the values for the design coefficients are B_p = 22.287 and δ = 171.676. From the B_P - δ diagram, the values of the optimal open water propeller efficiency η_O = 0.59 and the pitch ratio H/ D = 0.95 (mean propeller pitch H = 3800 mm) were determined. The calculated thrust force according to expressions (8) and (9) is adopted as F_T = 315 (kN) and the moment of the eccentric thrust force for the distance e_T = 0.16 m according to expression (3) is adopted as M_P = 50 kNm.

3.2. Comparison of deflection results applying the simplified model / Usporedba rezultata progiba primjenom pojednostavnjenog modela

Tables 5 and 6 show the results of the deflection of the shaft sleeve in the forward w_Af and aft w_Aa ends of the aft stern tube bearing and the difference in the deflection of the shaft sleeve at the edges of the stern tube bearing Δ w_L for the cases of loading of the shaft line by the weight of the propeller F_g (Figure 4) and by the moment of the eccentric thrust force M_P (Figure 5) . The results of the deflection for different constructive characteristics of the bearing L/ D and the length of the intermediate shaft l₁ were obtained using the method of initial parameters [12].

Table 5 Deflections w_Af and w_Aa (mm) and the difference in deflection Δ w_L (mm) for the case of loading by the weight of the propeller F_g

Tablica 5. Progibi w_Af i w_Aa (mm) te razlika progiba Δw_L (mm) za slučaj opterećenja težinom brodskog vijka F_g

Table 6 Deflections w_Af and w_Aa (mm) and the deflection difference Δ w_L (mm) for the case of loading by the moment of the eccentric thrust force M_P

Tablica 6. Progibi w_Af i w_Aa (mm) te razlika progiba Δw_L (mm) za slučaj opterećenja momentom ekscentrične porivne sile M_P

Using expressions (12) and (13), the obtained results of the difference in the deflection of the shaft sleeve at the edges of the stern tube bearing Δ w_L,approx are listed in Tables 7 and 8 for the cases of loading of the shaft line by the weight of the propeller F_g and by the moment of the eccentric thrust force M_P . Deviations from the results obtained by the method of initial parameters and expressions (12) and (13) are also listed in the Tables 7 and 8.

Table 7 Deviations of the deflection difference for the case of loading by the weight of the propeller F_g

Tablica 7. Odstupanja razlike progiba za slučaj opterećenja težinom brodskog vijka F_g

Table 8 Deviations of the deflection difference for the case of loading by the moment of the eccentric thrust force M_P

Tablica 8. Odstupanja razlike progiba za slučaj opterećenja momentom ekscentrične porivne sile M_P

The deviations in the above tables, for the case of loading by the weight of the propeller F_g of 3.15% and for the case of loading by the moment of the eccentric thrust force M_P of 0.8%, confirm the sufficient accuracy of the results obtained with expressions (12) and (13). For the bearing with constructive characteristic L/D = 2 and the intermediate shaft length of l₁ = 5 m, the deviations are below 1%.

3.3. The influence of the shaft sleeve elastic line on the selection of the stern tube bearing / Utjecaj elastične linije rukavca vratila na izbor statvenog ležaja

The correct selection of the aft stern tube bearing is the tribological problem. Its selection is strongly influenced by the eccentric thrust force. The change in the moment of the eccentric thrust force causes the change in the curvature of the elastic line of the shaft sleeve inside the stern tube bearing. It is important that these changes remain within the thickness of the lubricants layer h₀, that is, there must be a minimum thickness of the lubricant layer. In this paper, the change of the elastic line for different positions of the thrust force F_T is considered. For this analysis, the change in position of the thrust force F_T is related to the navigating regime, as explained in the introduction. When navigating straight ahead and astern, the position of the thrust force F_T is on the negative z-axis, while when turning it is on the positive y-axis (Figure 1). The results of the deflection of the shaft sleeve in the forward w_Af and aft w_Aa end of the stern tube bearing were used (from Tables 5 and 6 or Tables 7 and 8) and they are compared with the values for the minimum thickness of the lubricant layer h₀ from Table 9. It is necessary to discuss which stern tube bearing selection is favorable. The harmful impact of lubricating oil or polymer particles on the environment should also be considered. Table 9 shows the data for the minimum thickness of the lubricant layer h₀ of the classic oil-lubricated and the polymer water-lubricated bearings determined for the real example analysed in this paper [4].

Table 9 Parameters of stern tube slide bearings with the contact angle Ω =360°

Tablica 9. Parametri statvenih kliznih ležajeva obuhvatnog kuta Ω =360^o

The analysis was carried out for the constructive characteristic of the bearing L/D = 2 (length of the bearing is L = 600 mm) and the length of the intermediate shaft of l₁ = 5 m.

Figures 7, 8 and 9 show the elastic lines of the shaft sleeve for the assumed positions of the thrust force F_T of the navigation regimes mentioned. The values of deflection of the shaft sleeve at the edges of the stern tube bearing are given for: a) loading by the weight of the propeller F_g , b) loading by the moment of the eccentric thrust force M_P and c) total loading. The previous alignment of the shaft line is not taken into account.

During normal straight ahead navigation (Figure 7), the moment of eccentric thrust force M_P corrects the elastic line of the shaft sleeve caused by the weight of the propeller F_g , and fluid friction occurs in the stern tube slide bearing. The ship navigating at her steady-state speed of 15 knots. If such a regime is established and the sea during navigation is deep enough and also without significant waves, the thickness of the stern tube slide bearing lubricant layer is sufficient in relation to the curvature of the formed elastic line of the shaft sleeve (Figure 7c). In the case of minor disturbances in the navigation regime, the bearing enters the area of mixed friction. Hydrodynamic lubrication along the entire length of the bearing is achieved by adjusting the surface of the bearing and sleeve by running-in - wear.

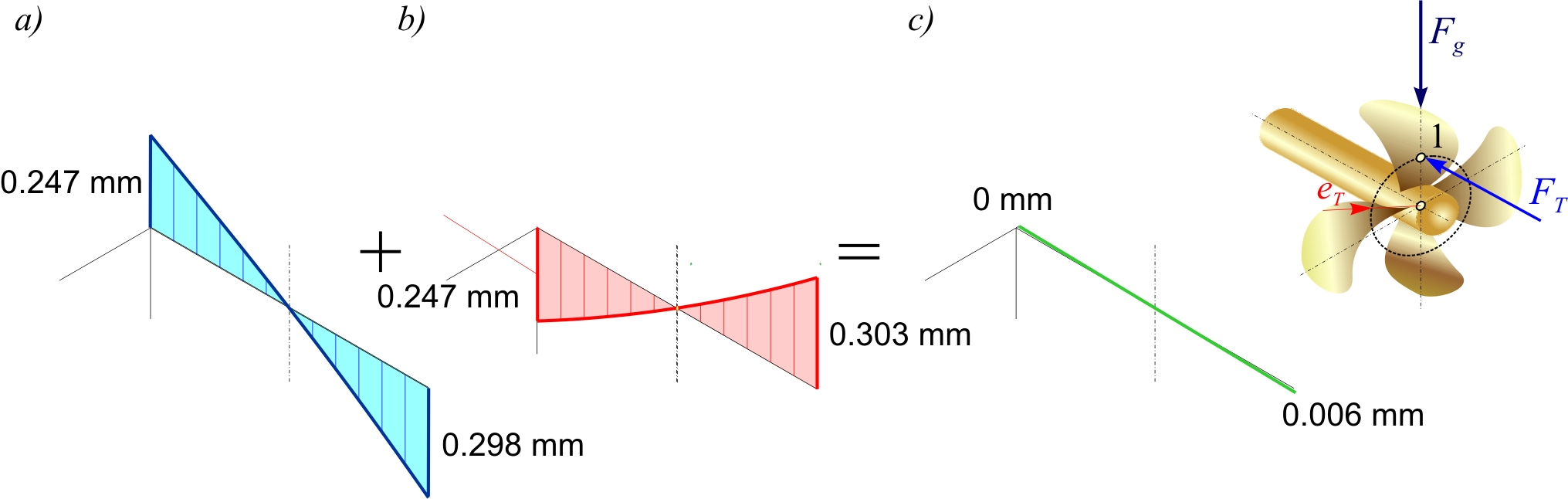
Figure 7 Elastic lines of the stern tube bearing sleeve for the case of navigating straight ahead

Slika 7. Elastične linije rukavca statvenog ležaja za slučaj plovidbe ravno naprijed

The turning of the ship during straight ahead navigation leads to changes in the curvature of the elastic line of the shaft sleeve inside the stern tube bearing (Figure 8). A greater thickness of lubricating oil is more suitable for these changes in the navigation regime. Here, edge wear occurs on the side surfaces of the aft and forward parts of the slide bearing bush (Figure 8c) and the stern tube slide bearing will enter the area of mixed friction [15].

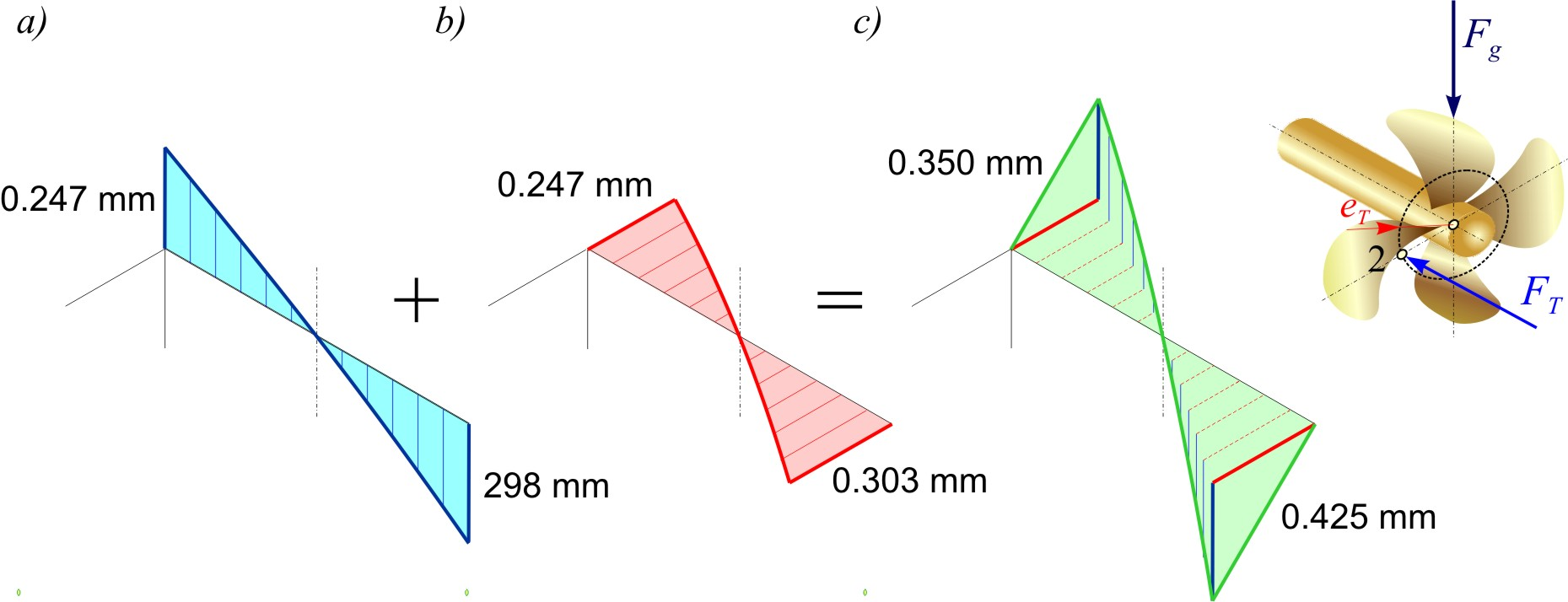
Figure 8 Elastic lines of the stern tube bearing sleeve for the case of turning

Slika 8. Elastične linije rukavca statvenog ležaja za slučaj skretanja

Strong disturbances in the operation of the stern tube bearing occur when the ship is navigating astern (Figure 9). Due to the greater resistance of the ship and the variable velocity field on the propeller, the equal amount of the thrust force F_T = 315 kN is assumed for this analysis with the position of action on the negative z-axis. In this case, the aft part of the surface of the slide stern tube bearing bush wears due to elastic deformations and the deflection of the shaft sleeve caused by the weight of the propeller F_g and the moment of the eccentric thrust force M_P (Figure 9c). It is possible that the stern tube slide bearing is in the transition area from mixed to semi-dry friction and vice versa.

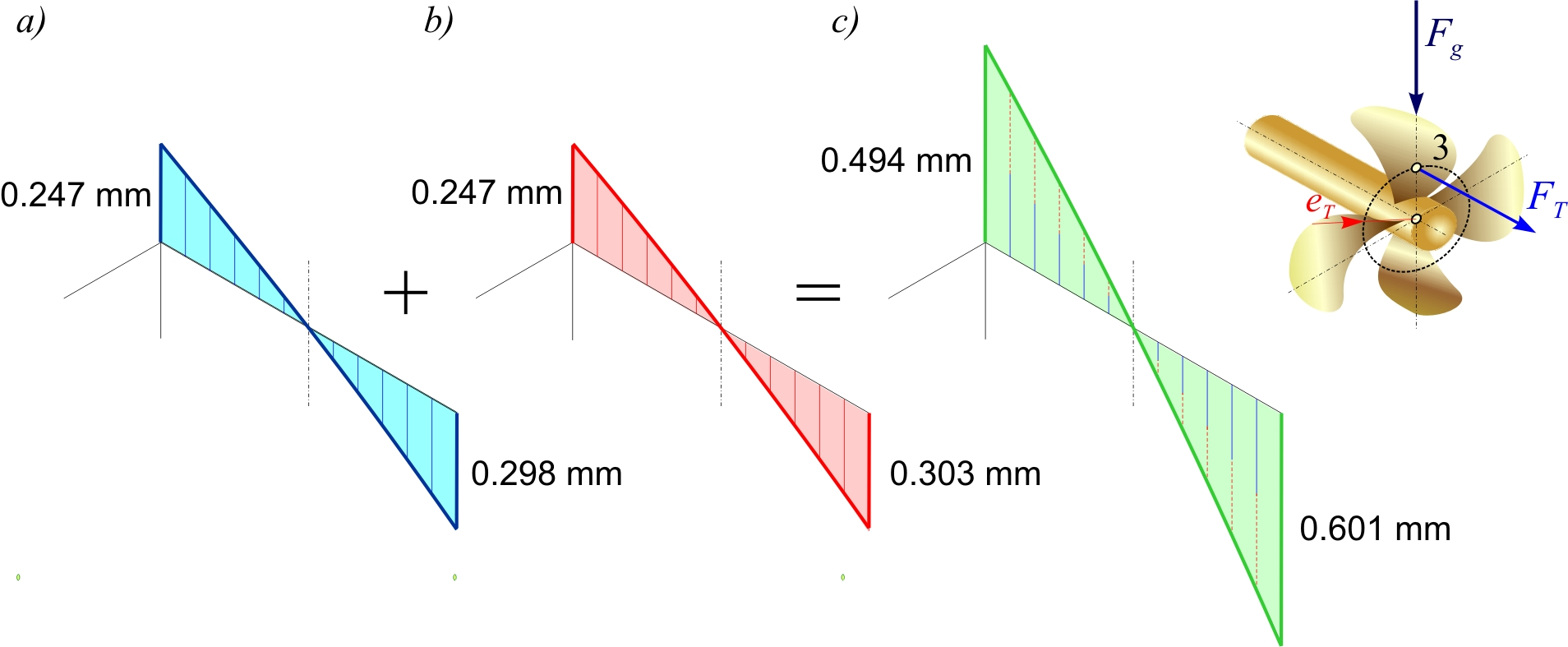
Figure 9 Elastic lines of the stern tube bearing sleeve for the case of navigating astern

Slika 9. Elastične linije rukavca statvenog ležaja za slučaj plovidbe krmom

The curvature of the elastic line of the shaft sleeve of the aft stern tube bearing, which is spatial in real cases, can sufficiently simulate the working area in which the stern tube slide bearing is located. The given diagrams, which are the result of simplified analytical models, show the state of the elastic line of the sleeve and the influence of its curvature on friction and wear of the material of the slide bearing bush for various cases of external loading. The calculated moment of the eccentric thrust force M_P only for the case e_T = 4%D, which was analyzed in this paper, already has a great influence on the working area of the stern tube bearing. Therefore, confirmation of the application of the simplified model is important for future analysis and research [16,17]. In this case, quick and reliable selection of the slide bearing bush and lubricant for the stern tube bearing lubrication can be expected.