1. INTRODUCTION / Uvod
A submarine is a type of watercraft that can operate independently under the surface of the water [1]. Regardless of their size, submarines are often referred to as boats, rather than ships. While the development of experimental submarines predates the 19th century, it was during this period that submarine design saw significant advancements and gained widespread adoption by several naval forces. Currently, submarines are used by a multitude of fleets, both of considerable size and small scale. Military applications include several strategic purposes such as engaging hostile surface vessels (including civilian commercial ships and military craft), countering submarines, safeguarding aircraft carriers, executing blockade operations, maintaining nuclear deterrent, conducting reconnaissance missions, launching conventional ground attacks, and clandestinely deploying special forces [2]. Civilian applications include various activities, such as maritime scientific research, salvage operations, exploration endeavours, and facility inspection and maintenance tasks. Submarines can undergo modifications for specific purposes, including search-and-rescue operations and maintenance of underwater cables. They are also used in tourism and underwater archaeology [3].
The realities of contemporary warfare, as well as the mission objectives outlined in Indonesia's military doctrines, necessitate that the Indonesian Armed Force (TNI) have a reasonable power projection capacity. Of course, ocean-going submarines are hardly an ideal solution because, like every weapon system, they have intrinsic strengths and shortcomings. Nonetheless, with the credible deterrence provided by such a fleet, the Indonesian Navy's (TNI-AL) mature expertise, and growing production and MRO support from domestic shipyards, submarines with long endurance capability are arguably prominent strategic assets with the best cost-benefit coordination for Indonesia [4].
Massive structures, control systems, power units, weapons systems, observation equipment, communications equipment, and navigational devices are the primary components of submarines [5]. Observation, communication, navigation, weapons, and electromechanical systems are the five divisions that comprise the majority of the equipment used onboard. Several submarine shape parameters have been investigated [6].
The German Type 209 diesel-electric submarine had significant success as the leading submarine for export sales from the late 1960s to early 21st century. In 1967, the Kieler Howaldtswerke shipyard supplied the Royal Hellenic Navy with four submarines weighing over 1000 tons each, which served as the first vessels of the Type 209 class [7]. The submarine design was originally derived from that constructed for Volksmarine, with a single-hull structure and spacious battery compartments. A 5000-horsepower electric engine, directly connected to the shaft, propelled the boat at speeds exceeding 20 knots. Submarines are assigned to a wider range of duties, prompting a transition to supercharged engines and resulting in enhanced performance [8]. Hydrodynamic analysis of the U209 type submarine under surface conditions was carried out in the presence of a high-flow velocity gradient [9]. The dimensions of the submarines expanded in accordance with the precise demands placed by diverse clients, necessitating supplementary room to meet enhancements in range, crew accommodation, augmented electronic apparatus, and heightened diving capabilities. The Type 209 family includes a range of submarines, all designed with the primary objective of minimising self-generated noise. Owing to the high volume of orders, each contract benefited from the latest advancements in research and technology, resulting in very low levels of radiated noise during both snorkelling and submerged cruising [10].
Submarine activities in the ocean pose several challenging issues [11]. One of these challenges is biofouling, which can negatively affect submarine performance [12]. Biofouling has been a notable concern in the maritime sector since the 1960s, owing to its detrimental effects on drag, fuel consumption, and greenhouse gas emissions [13]. Microorganisms (bacteria and algae) produce slimy layers, which facilitate this process. These layers transmit chemical signals via quorum sensing, which promotes the colonisation of larger organisms, such as barnacles, ascidians, and serpulids. In tropical seas, biofouling progresses within a time frame of 1–24 h, followed by the settling of invertebrate larvae and algal spores within 2–3 days, and the subsequent establishment of a macrofouling assemblage within 3–4 weeks [14].
The presence of microorganisms may result in corrosion, as shown by research on microbiologically influenced corrosion (MIC), which examines the activity of sulfate-reducing bacteria (SRB). Research has been conducted to observe and measure the quantity and behaviour of microorganisms, including the impact of biofilms on the corrosion of metallic surfaces. Biofilms of bacteria or the release of oxygen depolarisation during microbial metabolism may accelerate the corrosion of industrial equipment by creating a slime mass and altering the electrical potential of surfaces [15]. The submerged parts of the oceangoing vessels collect marine biofouling within a few moments of contact. Eventually, this build-up increases the physical drag of the vessel. Increasing the fuel consumption to maintain a certain speed or decreasing the speed at a maintained power results in vessel fouling drag [16].
Researchers in Indonesia classified biofouling into seven distinct categories [17]: ship drag [18], biological invasion [19], bacterial biofilms [20], biocorrosion [21], biosecurity risk management [12], geographical considerations [22], and mitigation strategies [23]. Researchers have conducted significant studies on the formation of bacterial biofilms, invasion of marine species, strategies for managing marine biosecurity risks, corrosion of materials in artificial seawater, and the importance of educating and raising awareness regarding the spread of non-native invasive species through vessel movements.
The primary aim of this study is to examine the drag experienced by a 209-type submarine using computational fluid dynamics (CFD) techniques[24]. The analysis was conducted using the Reynolds-averaged Navier–Stokes (RANS) method with the Menter Shear Stress Turbulence (SST) model. This study was performed on a submarine with six variations in roughness at a velocity of 9.7 knot to 29.1 knot. The CFD solver is briefly introduced, followed by a description of the numerical setup, which includes mesh creation and boundary conditions. The roughness effect was calculated to assess its effect on the drag experienced by the submarine.
2. METHOD / Metoda
2.1. Governing Equation / Osnovna jednadžba
Computational fluid dynamics (CFD) was used to predict the drag of the models. Utama et al. [25] conducted a study to determine the hull drag of a slender catamaran by using computational fluid dynamics (CFD), and their findings were favourable in comparison to the results obtained from testing. The Reynolds-averaged Navier-Stokes (RANS) technique is an equation that was established in three dimensions and used in a computational fluid dynamics (CFD) model. An unsteady incompressible flow, which was provided by ANSYS-CFX, was used to solve the flow problems present in the walls of the ship[26].
It has been demonstrated that the selection of turbulence models is of the greatest importance when applied to wake field modelling. The Shear Stress Transport (SST) turbulence model developed by Menter [27][28] was considered in this study. Many researchers have used and validated the SST model, and all have concluded that the model produces good results [29][30][31]. The fluid flow field was solved using the RANS solver, which is a component of ANSYS CFX. Equations (1), (2), and (3) describe the continuity, RANS, and SST turbulence equations, respectively.
Continuity equation:
(1)
In the continuity equation, ρ is the fluid density, t is the time, and Uj is the flow velocity vector field.
RANS equation:
(2)
The left side of the RANS equation (2) represents the change in the mean momentum of the fluid element to unsteadiness in the mean flow. This change is balanced by the mean body force (), the mean pressure field (), the viscous stress,, and apparent stress () to the fluctuating velocity field.
Menter’s SST equation
(3)
The Menter's Shear Stress Transport (SST) model integrates the beneficial aspects of the k–ω model to provide an improved model formulation suitable for many applications. To solve this objective, a blending function F1 is created, which has a value of one in the area closest to the solid surface and a value of zero in the flow domain farther away from the wall. The k–ω surface area of the walls and the k–ε model for the residual flow were both activated. This technique makes it feasible to use the appealing near-wall performance of the k–ω model to determine the sensitivity of the free stream.
The application of the Rhie–Chow algoritm method is employed to address the distinctive flow coupling that emerges from inter-phase drag within the ANSYS CFX. This technique is crucial for accurately representing the interactions between different phases of fluid flow, particularly in complex scenarios such as those encountered in computational fluid dynamics. A comprehensive examination of how this fluid coupling is managed, along with its integration into the velocity-pressure solution algorithm, is provided. The implications of this approach on the overall robustness and accuracy of the simulations are thoroughly analyzed, particularly in the context of three-dimensional modeling of submarines[32][33]. The convergence criterion used in both codes was established by assessing the residual error in the mass and momentum equations, using a predetermined threshold of 10-4 [34][35].
2.2. Modelling / Modeliranje
Figure 1 shows the hull geometry of the submarine. The main dimensions of the model are listed in Table 1.

Figure 1 Submarine Geometry Type U-209
Slika 1. Geometrija podmornice tipa U-209
Table 1 Main dimension of Submarine
Tablica 1. Osnovna dimenzija podmornice
| Dimension | U209 | Unit |
|---|---|---|
| Length Over All (LOA) | 62 | m |
| Hull Diameter (HD) | 6.2 | m |
| Wetted Surface Area (WSA) | 1449.1 | m2 |
| Displacement (∇) | 2088.6 | m3 |
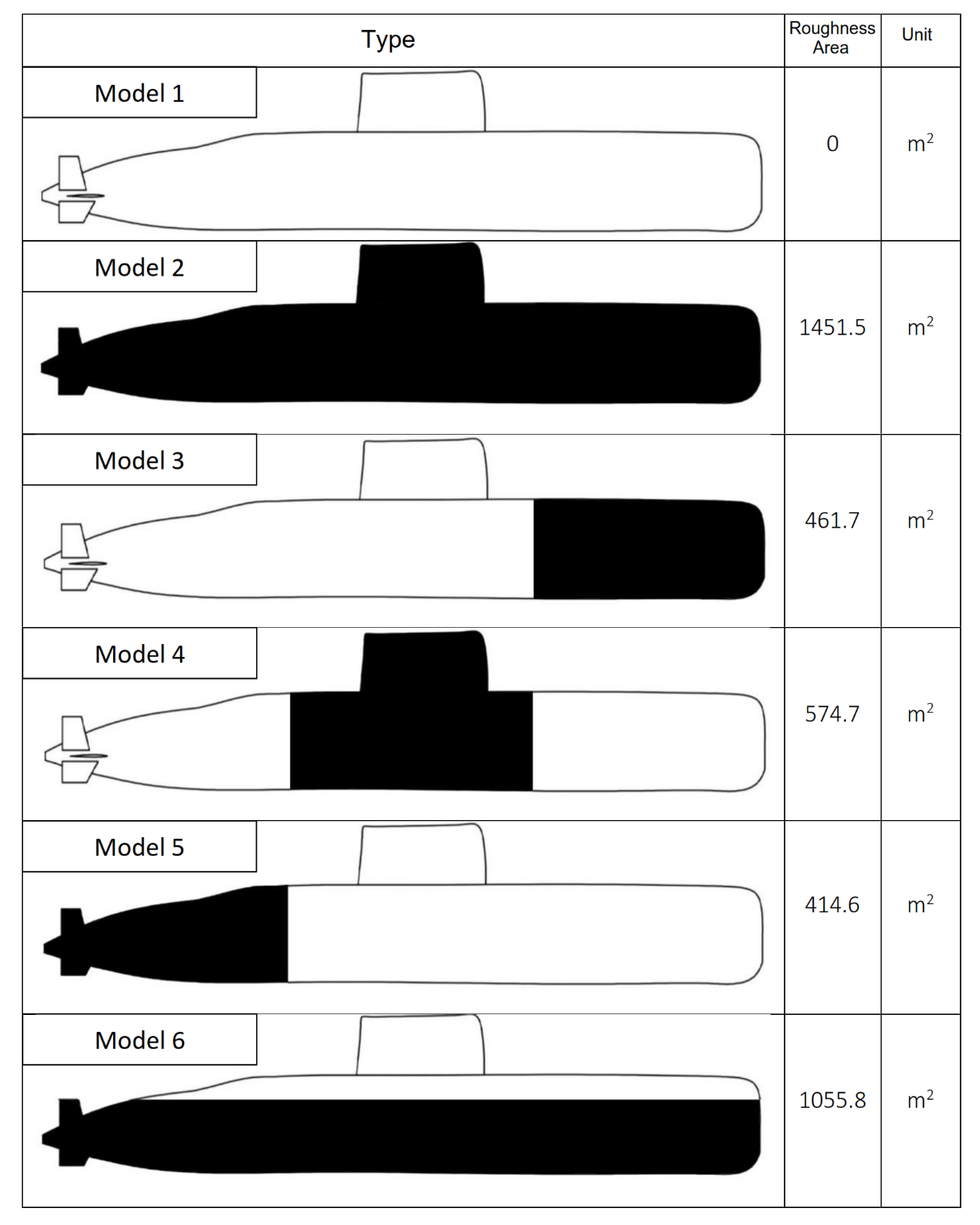
Figure 2 Specify the roughness model and its position.
Slika 2. Specifikacija modela hrapavosti i njezin položaj
Six distinct conditions were examined for marine biofouling growth (Small species brood lecithotrophic larvae) at a height of 200 μm at Indonesia [36] [37]: no fouling on the entire surface, fouling exclusively on the forward one-third of the hull, fouling exclusively on the middle one-third of the hull, fouling exclusively on the stern one-third of the hull, and fouling exclusively on the lower portion of the hull (and aft control surfaces). The latter condition was selected to symbolise a practical circumstance in which the boat's upper surfaces are comparatively easy to clean when raised above the water but remain submerged. The variations in the roughness area among the submarines are illustrated in Figure 2.
2.3. Domain / Domena
The proposed computational domain is 2 L forward, perpendicular to the front, at the velocity inlet, and 5 L towards the rear, perpendicular to the outlet pressure. By adjusting the transverse and vertical directions to 2 L–3 L [12], we were able to prevent the negative impact of reverse flow on the borders of the area. The domain size and boundary conditions are illustrated in Figure 5. The inlet flow velocity is defined as velocity of 9.7 knot to 29.1 knot, and the outlet is defined hydrostatic pressure; the hull body is identified as a fixed boundary immersed in fluid and a no-slip condition (taking into account the presence of viscous drag); the bottom is given a free-slip condition; the top wall is given a free-slip condition; and the side walls are given a free-slip condition (considering the absence of frictional drag), as shown in Figure 3.

Figure 3 Computation Domain
Slika 3. Računalna domena
The use of a Design Modeller was required to complete the mesh construction process for this investigation. A combination of structured and unstructured meshes was used to discretise the computational domain. Considering the intricate geometrical features of the hull, a mesh consisting of triangular elements is constructed on the hull surface. Subsequently, the boundary layer is refined using prism elements generated by expanding the surface mesh node. Inflated tetrahedral elements were used to populate the area close to the boat, whereas an unstructured mesh with grid generation was used to reduce the total number of components in the distant field (as illustrated in Figure 4).
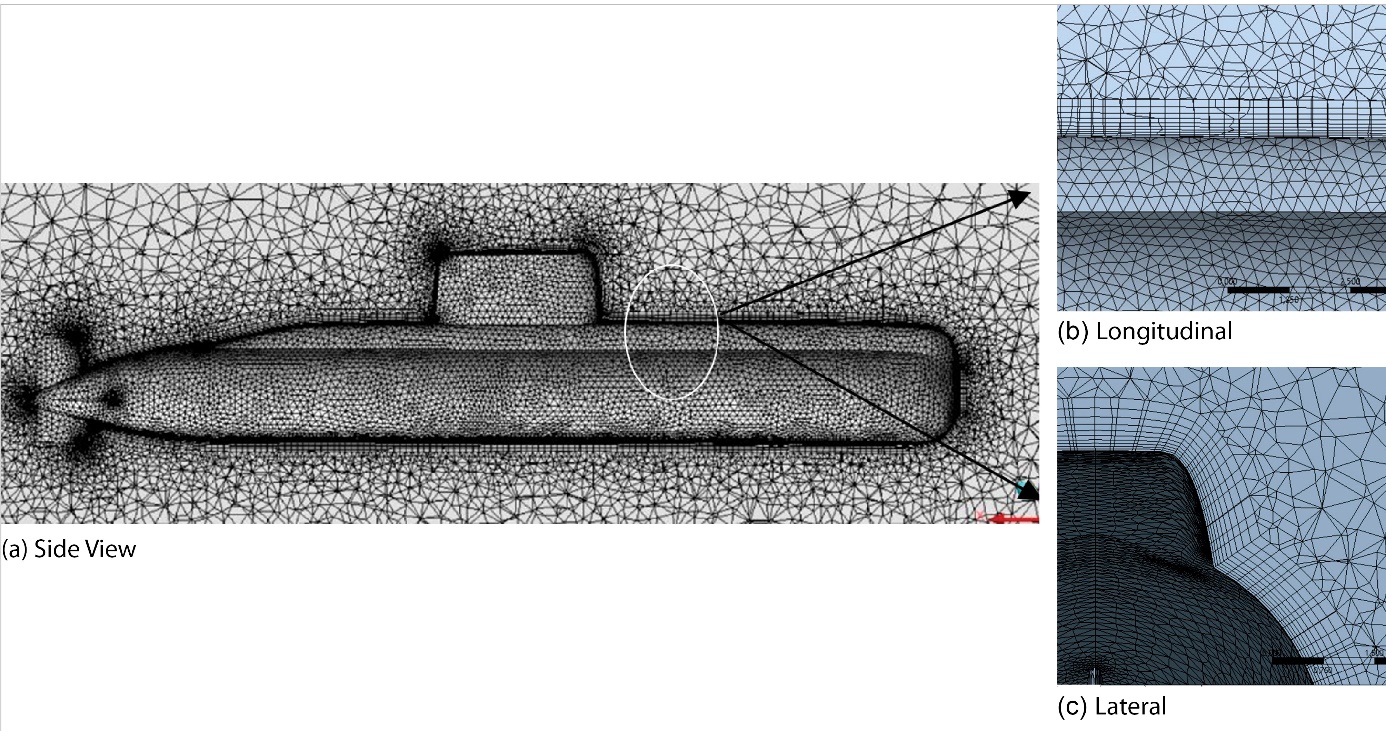
Figure 4 Side view of Hybrid Mesh
Slika 4. Bočni prikaz hibridne mrežice
It is possible that a fine mesh will always provide trustworthy results in ANSYS CFX; however, because of the large number of elements, it also increases the amount of time and money required for calculation. During the computational process, mesh size is an important factor to consider. Mesh convergence was performed on both subsurface and surface models, as illustrated in Figure 5. For U209, ideal mesh convergence was achieved, which led to a total mesh count of 1.83 million. This convergence was supported by the results of Anderson, who demonstrated a difference of less than 2% in the overall drag coefficient [38].
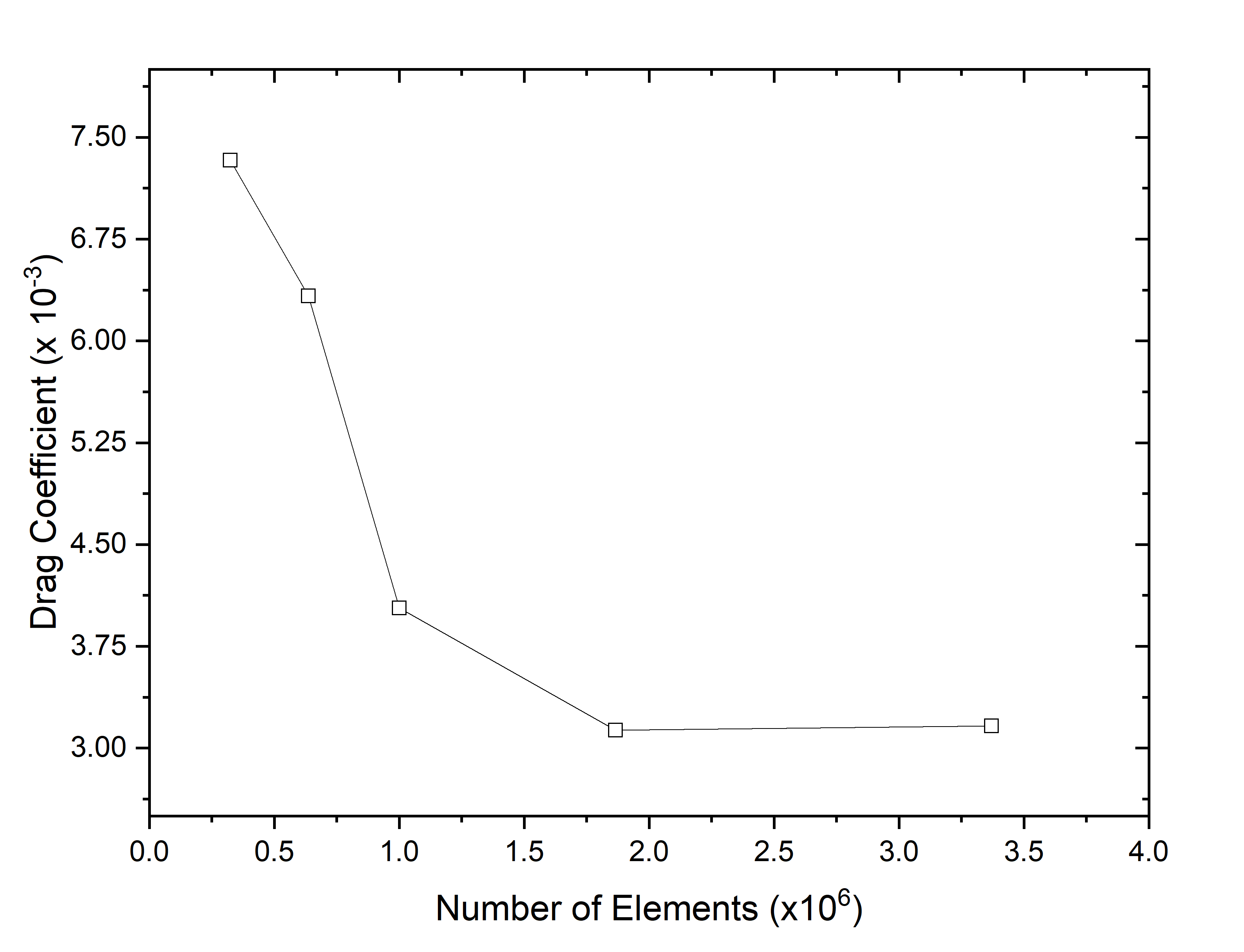
Figure 5 Grid Independence Study
Slika 5. Studija bez grafičkoga prikaza
Convergence studies of the parameters were performed by following a systematic refinement process to create multiple solutions. The numerical uncertainty of the CFD model was based on the data in Table 2. Richardson’s extrapolation method for grid convergence is a suitable choice for estimating mesh errors [39]. A convergence study was conducted based on three varying mesh resolutions which were categorised into coarse, medium, and fine meshes. The mesh was varied by modifying the face sizing while maintaining body sizing with a constant element size. The inflation layer was kept constant throughout the analysis because the mesh resolution was based on a standard wall calculation, as shown in Table. 3.
Table 3 Three varying mesh resolution details
Tablica 3. Tri varijabilna detalja rezolucije mrežice
The process was the same for time and other parameter studies. As for the refinement ratio, ri, the recommended value is , because the value is large enough to be sensitive to parameter changes, and small enough to be used to generate at least three successive solutions. A larger refinement ratio may be used; however, the mesh size must be at least three. Based on the formulas in the equation section, the outcomes were calculated, and are presented in Table 4.
Table 4 The uncertainty analysis performed for Submarine
Tablica 4. Analiza nesigurnosti izvršena za podmornicu
The convergence conditions of this system must first be clarified to assess the extrapolated values from the above equations. The convergence conditions are as follows:
Monotonic convergence: 0 < Ri < 1
Oscillatory convergence: Ri < 0
Divergence: Ri > 1
Generalised Richardson Extrapolation was applied to estimate the errors and uncertainties for monotonic convergence. For oscillatory convergence, the results exhibit oscillations. In instances of divergence, the results diverged, rendering it impossible to determine errors and uncertainties. In instances of divergence, it is crucial to carefully analyse the results to identify any errors and uncertainties that may have contributed to divergence. A thorough investigation of the data and methods used can help determine the underlying causes of divergence and prevent similar issues from arising in future studies.
The grid convergence index (GCI) is widely accepted for evaluating the quality of grid convergence. This metric was calculated during the refinement steps, and the GCI for the steps taken from grids 4 to 3, 3 to 2, and from 2 to 1 was calculated. In this process, e represents the error between the two grids and Fs is the safety factor (Fs=1.25). To ensure the safety of the grid, the error between the two grids was calculated and compared using the safety factor (Fs = 1.25). The value of e represents the level of discrepancy, which must be maintained within the acceptable limits for the grid to function properly. A study of grid refinement, examination of GCI values for integration, and analysis of point variables demonstrated a progressive decrease in these values as the grid system was refined. The appropriateness of using a finer grid for further analysis was indicated by the extrapolated values calculated through Richardson extrapolation, as the GCI values for all variables under investigation were less than 5% at grid levels 1–3 [40].
The resistance converged, as is evident from the graphs, indicating that the mesh converged with varying mesh fineness. Although a fine mesh was chosen for the analysis to provide higher accuracy, it is essential to select a mesh that minimises the investigation error. However, it is important to note that the selection of an appropriate mesh size for the analysis is crucial for minimising the errors that may arise from the investigation. In addition, the selection of an appropriate analytical method is crucial for ensuring accurate and reliable results. It is important to carefully consider the strengths and limitations of each method and choose the one most suitable for the specific research question and data being analysed.
3. RESULT AND DISCUSSION / Rezultati i rasprava
The results of the CFD method used to calculate the drag of the type 209 submarine are shown in Figure 6, which can be seen here. The roughness of the surface of the submarine hull is shown in this figure as the reason for the increase in drag. Under full hull roughness, the average increase in drag was 40.1%, whereas under partial hull roughness, the average increase in drag was between 11.0% and 15.2%. This can be understood due to the impact of the wetted surface area affected by biofouling; as the area increases, the resistance it generates also becomes greater.
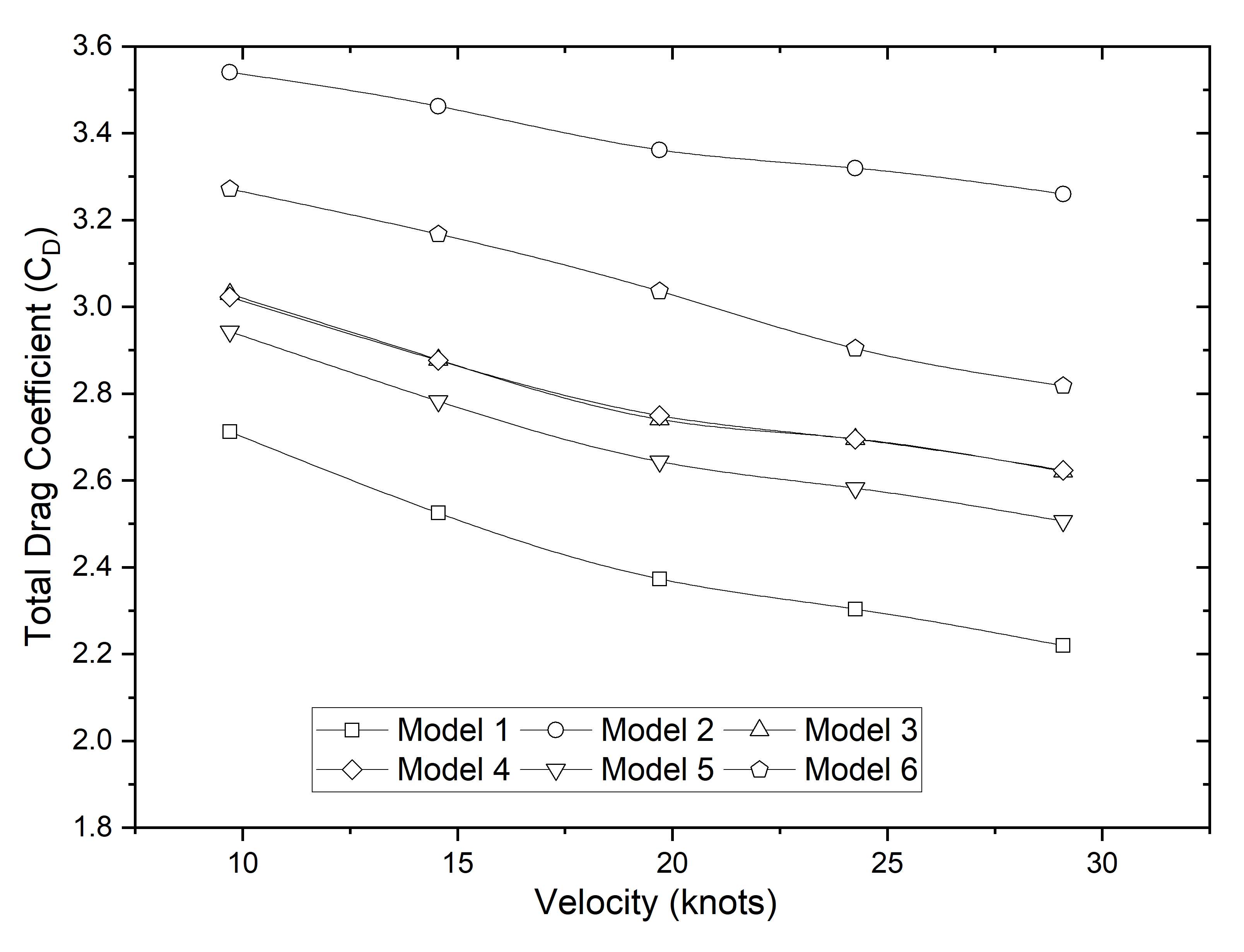
Figure 6 Drag coefficient of various submarine models
Slika 6. Koeficijent otpora za različite modele podmornica
A fascinating occurrence occurred in Models 3 and 4, where there was a roughly comparable increase in drag, that is, an average of 15.2% in both models when compared to Model 1 with a smooth hull. This comparison provided an understanding of this phenomenon. This is because both models have essentially the same roughness plane, which is perpendicular to the direction in which the water flows. All visualisations are shown at a speed of 29.1 knots to observe the differences in turbulence on smooth and rough surfaces. There was a large increase in drag caused by the roughness of the hull. According to Figure 7, this is owing to an increase in the amount of friction force, which can be seen as an increase in the amount of turbulence in the region of the submarine hull.

Figure 7 Cross section of a submarine hull
Slika 7. Poprečni presjek trupa podmornice
The longitudinal division of the hull was divided into three component segments in greater detail. An in-depth explanation of the increase in drag that occurs as a result of the partial hull roughness is provided in this section. The roughness at the front of the submarine (Model 3) causes an increase in drag, which is, on average, 15.2% higher than the overall drag. As shown in Figure 8, the addition of drag caused by roughness in the front third of the submarine occurs in a fluctuating manner. This is because the roughness causes turbulence.
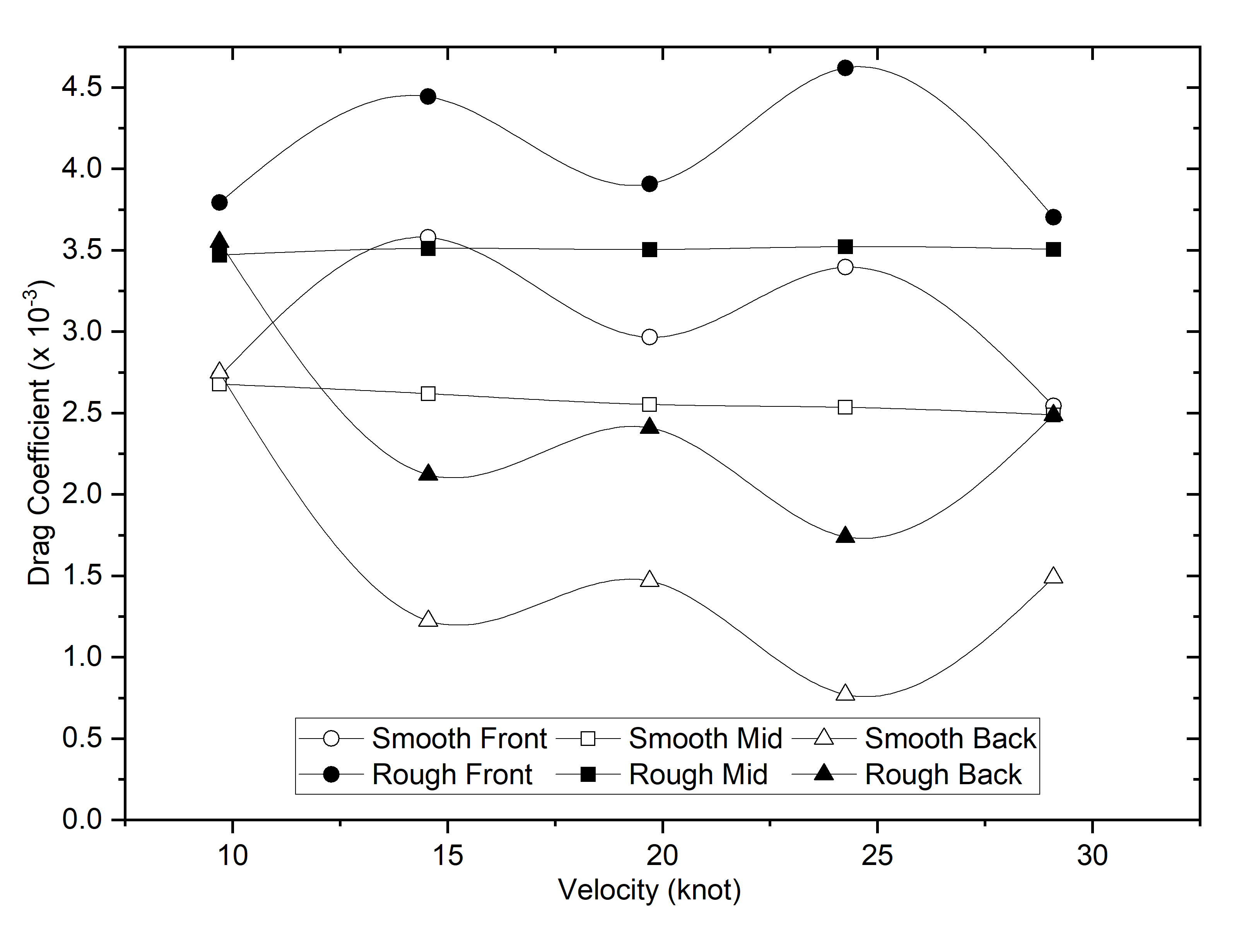
Figure 8 Drag of Submarine for each segment
Slika 8. Povlačenje podmornice za svaki segment
A correlation can be shown between the increase in speed simulated on the submarine and the increase in drag that then occurs. Because of the roughness of the hull at the front, which results in an increase in the frictional drag, the difference that occurs is caused by this. As shown in Figure 9, the influence of roughness also results in a turbulence effect in regions with roughness. On the surface of the smooth front third of the submarine hull, the turbulence effect is characterised by a slight turbulence area of approximately 0.42 m2s-2. This is because the turbulence effect is characterised by a change in the Turbulence Kinetic Energy value. Meanwhile, when the roughness conditions in the front third of the submarine were 200μm, massive turbulent changes occurred, accompanied by a turbulence kinetic energy value that exceeds 0.92 m2s-2.
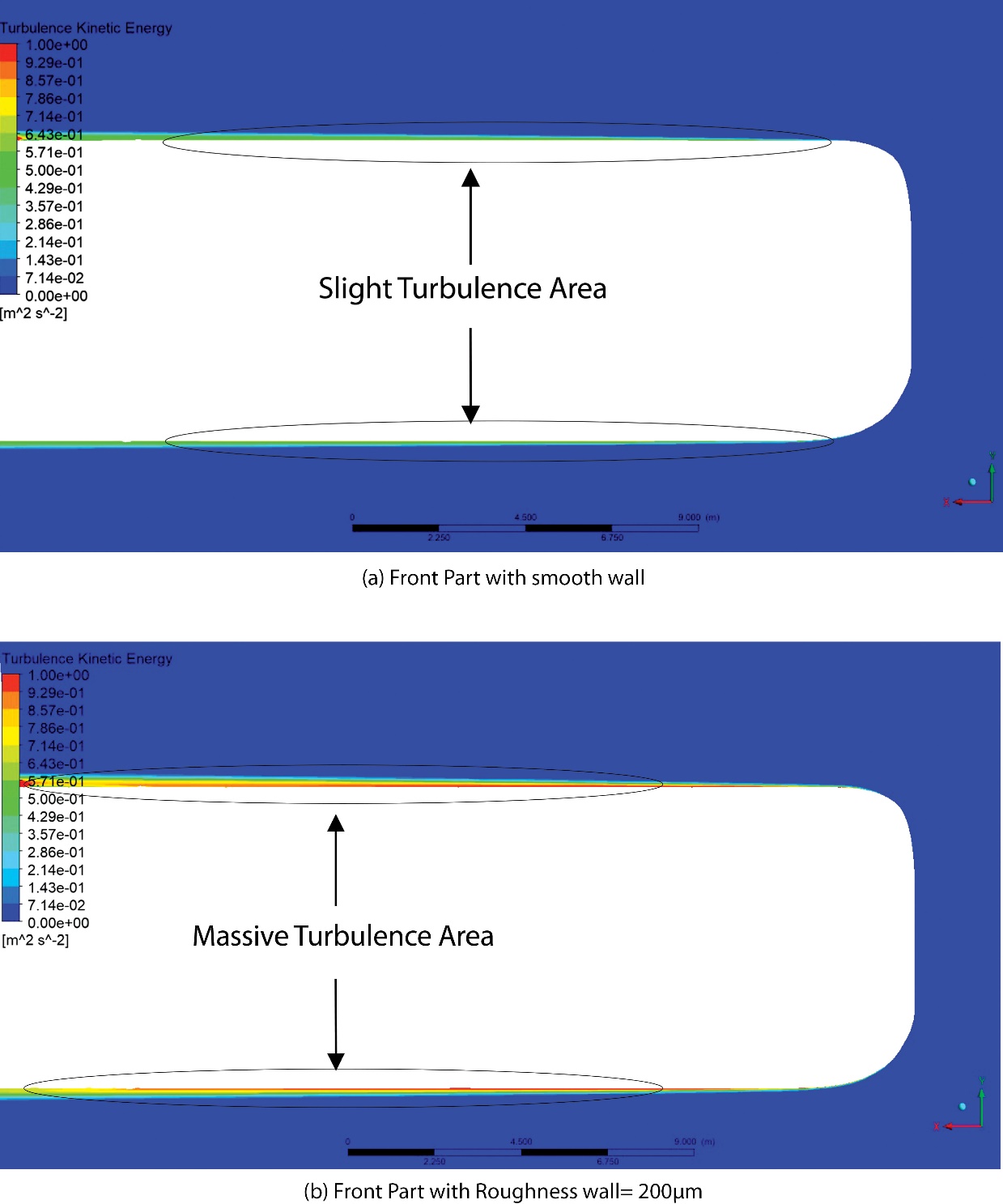
Figure 9 Turbulence Kinetic Energy of Front Hull
Slika 9. Kinetička energija turbulencije prednjega trupa
Furthermore, as shown in Figure 10, the surface roughness of the middle section of the submarine (Model 4) caused an increase in the drag, ranging from 11.4% to 18.2%. The effect of roughness in the middle part of the submarine hull tends to be linear, resulting in a larger difference in value than that in other parts of the hull. The relative shape of the roughness field data, which appeared to be perpendicular to the flow direction, caused this phenomenon. A correlation can be drawn between the increase in speed simulated on the submarine and the subsequent increase in drag. The presence of sails and hull roughness in the middle of the submarine were the components responsible for the observed differences. The massive colour change that occurs in the flow behind the sail and on the submarine hull, as depicted in Figure 10, is a clear indication of the increase in turbulence.
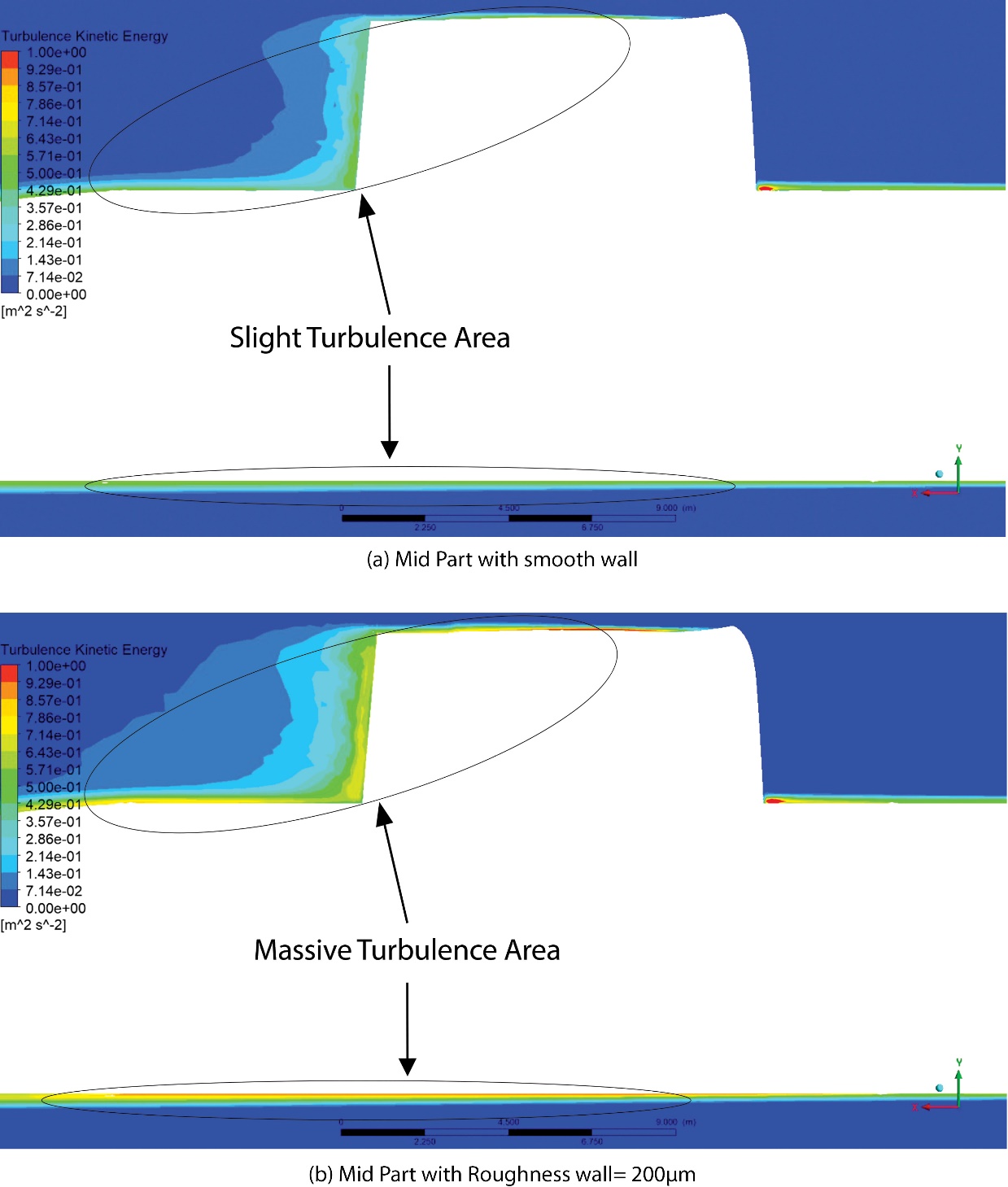
Figure 10 Turbulence Kinetic Energy of Mid Hull
Slika 10. Kinetička energija turbulencije srednjega trupa
Furthermore, the increase in drag caused by the roughness in the middle of the submarine was approximately 11%. The increase in drag that occurs under this condition is typically less significant than that under the previous condition. Following the numerous surface indentations in Model 5, a turbulent flow is possible under these conditions. Under these conditions, the drag effect of roughness was less than that of a flat surface. As illustrated in Figure 11, this has the additional effect of increasing the fluctuating drag.
The increase in drag that occurs is consistent with the increase in speed simulated in the submarine when roughness is present in the rear third. Figure 11 (a) shows that the rudder at the back of the submarine causes turbulence; however, this turbulence is relatively minor and similar to that at the back of the submarine hull. In addition, there was an increase in the turbulence values, which were approximately 62.3% higher in the same section. This difference that takes place is due to the roughness of the hull in that particular section, which causes an increase in frictional drag. It is also possible for the roughness to cause turbulence effects in regions with roughness, as shown in Figure 11 (b).

Figure 11 Turbulence Kinetic Energy of Back Hull
Slika 11. Kinetička energija turbulencije stražnjega trupa
For Model 6, which has a rough surface area of 1155.8 square metres at the bottom of the submarine, the surface navigation procedure is the reason for the increase in the amount of drag experienced by the submarine. Under these circumstances, there was a 28.5% increase in the average drag when smooth hull conditions (model 1) were present. As shown in Figure 12, the turbulence at the top of the submarine did not undergo substantial changes. This is because the surface of the submarine remained the same (smooth) in Figures 12(a) and 12(b). However, notable variations are observed in the bottom section of the submarine. These variations include minute alterations in the turbulence region shown in Figure 12(a) and enormous turbulence areas shown in Figure 12(b). Having a roughness(ks) of 200 μm has the effect of raising the frictional drag, which in turn leads to an increase in the turbulent kinetic energy value of approximately 57%.

Figure 12 Turbulence Kinetic Energy of Hull
Slika 12. Kinetička energija turbulencije trupa
This study that has been conducted demonstrates that there is a substantial increase in the resistance of the submarine, particularly when the conditions on the entire surface of the submarine are rough, with an increase in resistance of up to 46.9% under these circumstances [24]. Considering that the DARPA submarines in question have the same roughness configuration, the findings of this study are pertinent. Subsequently, the impact of various marine biofouling features on ship resistance [41]. The overall roughness of a surface significantly impacts drag, primarily because it encompasses a larger area, resulting in an increased wetted surface area that interacts more intensely with the boundary layer. This broader coverage leads to a more pronounced effect on the flow dynamics, ultimately contributing to higher drag forces. The interaction between the rough surface and the fluid flow is critical, as it disrupts the smooth flow patterns, thereby enhancing turbulence and increasing resistance. In contrast, while partial hull roughness does play a role in influencing drag, its effect is generally less significant compared to that of overall roughness. The localized nature of partial roughness means that it does not engage with the fluid flow to the same extent as a more extensive rough surface. Consequently, the impact of partial hull roughness on drag is diminished, making it a less critical factor in the overall assessment of drag forces in fluid dynamics.
This issue is pertinent to the study of the potential effect of biofouling roughness on the full-scale powering performance of submarines [42][43]. A high-roughness modelling technique was used to define biofouling that attaches to the surface of a submarine. This research is beneficial for providing operators with suggestions that might enhance submarine performance. An integrated strategy that merges preventive techniques with advanced underwater technology, routine assessments, and heightened environmental consciousness can significantly enhance the operational effectiveness of submarines while reducing the adverse effects associated with biofouling [44]. By employing a comprehensive methodology, submarines can proactively address potential issues before they escalate, ensuring that their performance remains optimal in various marine environments [45].
The CFD method was used to assess the drag on a type 209 submarine, highlighting that the roughness of its surface significantly impacts drag levels. When the hull was entirely rough (Model 2), drag rose by 40.1%. For particularly rough hulls, the average drag increase ranged from 11.0% to 15.2%. Models 3 and 4 showed similar drag increases, averaging 15.2% compared to Model 1, which had a smooth hull. This increase was attributed to rough surfaces aligned with the water flow, enhancing friction and turbulence in those areas. A detailed analysis of the hull's longitudinal segments revealed how partial roughness contributed to drag. The increase in submarine velocity also corresponded to higher drag in the rear third (Model 5) due to roughness. The surface condition (Model 6) is largely responsible for the increase in the drag experienced, which has a lower surface area.
The roughness of the submarine hull significantly affects the drag, with increases ranging from 11.0% to 40.1% depending on the specific area of roughness. The presence of rough surfaces leads to increased friction force, turbulence, and drag, with different sections of the hull showing varying levels of impact on the drag based on the surface roughness. Furthermore, the degree of surface roughness also affects the water flow around the hull, which ultimately affects the overall performance and energy efficiency of the submarine. A holistic approach that combines preventive measures, regular inspections, and environmental awareness can help submarines maintain operational efficiency while minimizing the impact of biofouling. For future work, it is also important to consider the degree of surface roughness when evaluating the performance and energy efficiency of submarines.
Author Contributions: Sutiyo: calculations, data collection, writing and editing, visualisation; Bagiyo Suwasono: conceptualisation, methodology, and review; Ahmad Nasirudin: methodology, formal analysis, and review; I Ketut Aria Pria Utama: funding acquisition, concept design, data analysis, review, and editing.
Funding: This study was supported by a research collaboration scheme between LLDIKTI VII, as designated by Universitas Hang Tuah, and Institut Teknologi Sepuluh Nopember, with contract number 2273/PKS/ITS/2023.
Conflict of interest: None.
Acknowledgment: The authors would like express their sincere gratitude to the Institut Teknologi Sepuluh Nopember for supporting the research financially under a collaborative research scheme called Pakerti LLDikti Batch 2 with contract number 2273/PKS/ITS/2023, which appointed Universitas Hang Tuah in this instance.
