1. UVOD
Vozilo je tijekom vožnje izloženo utjecaju neravnina na cesti / kolniku. Te neravnine (izbočine i ulegnuća) mogu nastati na pojedinim dionicama kolnika tijekom vremena uslijed prolaska teških teretnih vozila, slijeganja tla i slično, a mogu biti i namjerno postavljene na cesti kao naprave za smirivanje prometa (NN 92/2019). Prijelaz kotača preko lokalne neravnine rezultira tzv. prijelaznim ili tranzijentnim vertikalnim odzivom vozila. Pravilnim odabirom vrste ovjesa te proračunom njegovih parametara može se uvelike utjecati na vibracijski odziv vozila. U tom smislu, svrha ovjesa je povećanje udobnosti putnika tijekom vožnje te osiguranje stabilnosti i upravljivosti vozila. Postoji više vrsta izvedbi mehanizma ovjesa no kad se analizira dinamika ovjesa često se koriste modeli sa koncentriranim parametrima, tj. opis pomoću ovješene i neovješene mase, opružnog i prigušnog elementa (Reza, 2008).
Za analizu dinamike ovjesa koriste se četvrtinski (¼ model), polovinski (½ model) i puni model ovjesa vozila. Četvrtinski model (Shelke i dr. 2018) opisan je ovješenom masom (odgovara ¼ ukupne mase vozila), neovješenom masom (masa kotača), koeficijentima krutosti i prigušenja te služi samo za analizu vertikalnog translacijskog gibanja. Sukladno tome, ½ model ovjesa (Shahriar i dr. 2016,Shelke i Mitra, 2018) koristi polovicu od ukupne mase vozila i dvije neovješene mase a puni model ovjesa (Radelja i dr. 2007) razmatra ukupnu masu vozila i sva četiri kotača. ¼ model ima dva stupnja slobode gibanja, ½ model ima četiri stupnja slobode gibanja, a puni model sedam stupnjeva slobode gibanja. Razlikujemo dvije vrste ½ modela ovjesa, pri čemu prvi razmatra posrtanje ovješene mase (zakretanje oko poprečne osi), a drugi naginjanje ovješene mase (zakretanje oko uzdužne osi vozila).
U ovom radu razmatra se ½ model ovjesa sa posrtanjem ovješene mase (Obajdin, 2017). Takav model je prikladan za analizu dinamike ovjesa vozila prilikom prelaska umjetne izbočine na ravnoj dionici ceste. Za osobno vozilo danih karakteristika analiziran je utjecaj dodavanja tereta na odziv ovjesa, tj. uspoređivani su slučajevi odziva bez i sa dodatnom masom tereta. Numeričke simulacije provedene su u programskom paketu Matlab/Simulink. Usporedba rezultata simulacija dana je u vidu maksimalnih vrijednosti odziva (pomaka i ubrzanja težišta vozila i kotača) pri brzinama vožnje 20 km/h, 30 km/h i 50 km/h. Naposljetku, prikazani su odzivi vertikalnih i kutnih pomaka i ubrzanja težišta vozila, pri brzinama 30 km/h i 50 km/h u vremenskoj domeni.
2. ½ MODEL VOZILA – POSRTANJE OVJEŠENE MASE
Vozilo je tijekom vožnje izloženo djelovanju neravnina na cesti. Pravilnim odabirom ovjesa ostvaruje se povećanje udobnosti vozača i putnika tijekom vožnje te osiguranje stabilnosti i upravljivosti vozila. Odabir vrste i parametara ovjesa često predstavlja kompromis različitih zahtjeva tj. vozilo se kako numerički tako i eksperimentalno testira u različitim uvjetima vožnje. Kako je cilj ovog rada dati usporedbu odziva za slučajeve prelaska vozila preko umjetne izbočine na ravnoj cesti, valjanje neće imati bitnijeg utjecaja te se stoga razmatra ½ model ovjesa sa posrtanjem ovješene mase.Slika 1 prikazuje vozilo sa svim stupnjevima slobode gibanja.
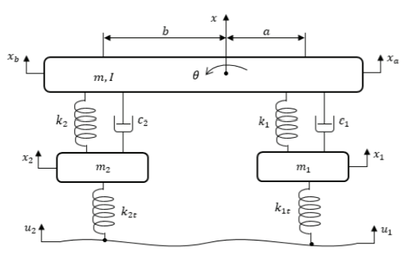
½ model sa posrtanjem sastoji se od ovješene mase kojoj odgovara polovina mase vozila m i polovina momenta inercije posrtanja (oko poprečne osi) J, neovješene mase prednjeg kotača m₁ i neovješene mase zadnjeg kotača mase m₂ (slika 2).
Krutost opruge i prigušenje prigušivača prednjeg dijela vozila opisani su koeficijentima k₁ i c₁, a zadnjeg dijela vozila koeficijentima k₂ i c₂. Krutosti guma prednjeg i zadnjeg kotača su k₁ₜ i k₂ₜ. Oznake u₁ i u₂ predstavljaju pobudu podloge na prednji i zadnji kotač. Četiri nezavisne koordinate kojima se opisuje gibanje su: (1) vertikalni pomak težišta prednjeg kotača y₁, (2) vertikalni pomak težišta zadnjeg kotača y₂, (3) vertikalni pomak težišta vozila y te (4) kutni zakret vozila oko poprečne osi θ. Drugim riječima, model omogućuje analizu vertikalnog gibanja vozila i kotača te kutnog gibanja, odnosno, posrtanja vozila (engl. pitch motion). Primjenom 2. Newtonovog zakona dobivene su četiri diferencijalne jednadžbe gibanja:
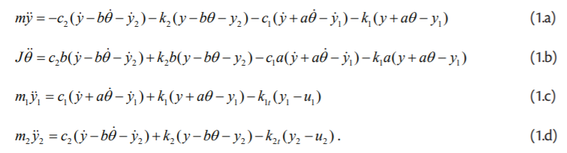
3. UMJETNE IZBOČINE
Prema Pravilniku o prometnim znakovima, signalizaciji i opremi na cestama (NN 92/2019) umjetne izbočine su gotovi modularni proizvodi od gume ili plastike, a postavljaju se prije zone smirivanja prometa preko jedne polovine ili po cijeloj širini prometne trake, većinom u stambenim ulicama. Ovisno o ograničenju brzine, prema dimenzijama razlikuju se tri tipa izbočina:
za brzine vožnje 50 km/h ili manje, širina ne smije biti manja od 60 cm, a visina ne smije prelaziti 3 cm,
za brzine vožnje 40 km/h ili manje, širina ne smije biti manja od 90 cm, a visina ne smije prelaziti 5 cm,
za brzine vožnje 30 km/h ili manje, širina ne smije biti manja od 120 cm, a visina ne smije prelaziti 7 cm.
Umjetna izbočina na koju nailazi kotač može se opisati funkcijom parabole:

gdje je H maksimalna visina izbočine, L maksimalna duljina izbočine te x prijeđeni put, koji se može odrediti kao umnožak brzine vozila v i vremena prelaska preko prepreke t, kako slijedi:

Koeficijent p u jednadžbi (2) dobiven je iz poznatih uvjeta u trenutku t = 0 (x = 0 i u₁ = 0), primjenom čega slijedi:

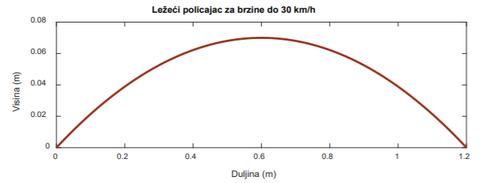
Matematički model umjetne izbočine za brzine vozila do 30 km/h prikazan je naslici 3.
4. NUMERIČKI MODEL
Radi jednostavnije implementacije modela vozila opisanog jednadžbama (1) u programski paket Matlab/Simulink iste su svedene na slijedeći oblik (Obajdin, 2017):
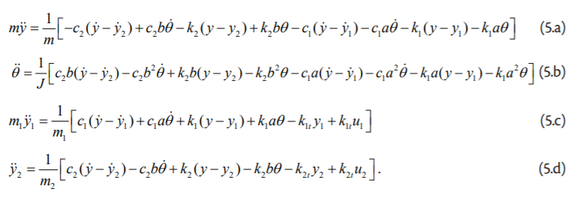
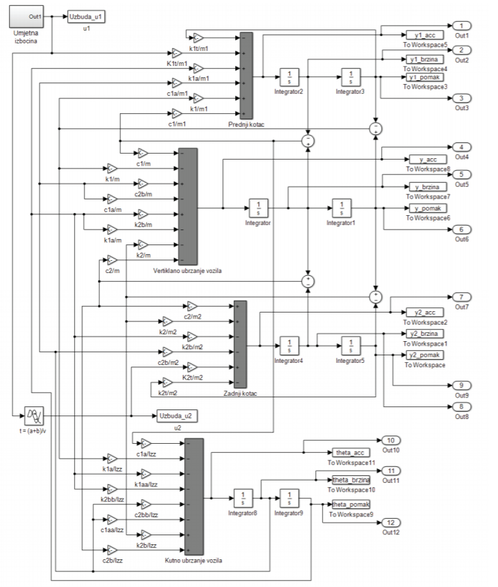
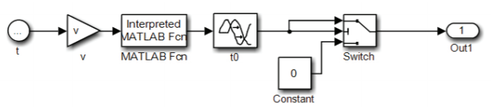
Na temelju jednadžbi (5) izrađen je Simulink model, kao što je prikazano naslici 4. Ovim modelom prati se struktura matematičkog modela (tok informacija), a ne fizikalna struktura stvarnog sustava (tok energije). Za dobivanje numeričkog riješenja običnih diferencijalnih jednadžbi (5) u programu Matlab/Simulink korištena je funkcija ode45, kojom se implementira Runge-Kutta metoda s promijenjivim vremenskim korakom.
U podsustavu Umjetna izbocina naslici 4, definirana je pobuda koja djeluje na prednji kotač, kako je prikazano naslici 5. Umnožak brzine i vremena (v·t) je ulazni signal u Matlab funkciju (MATLAB Fcn), gdje se na temelju izraza (2) definira pobuda prednjega kotača kao:

U bloku t0 definira se trenutak t₀ u kojem vozilo nailazi na prepreku (u ovom radu t₀ = 0.5 s). Pobuda zadnjeg kotača u₂ jednaka je pobudi prednjeg kotača (u₂ = u₁) i vremenski je pomaknuta za iznos:

gdje su a i b udaljenosti prednjeg i zadnjeg kotača od težišta vozila, odnosno njihova suma predstavlja vrijednost međuosovinskog razmaka.
5. REZULTATI SIMULACIJE
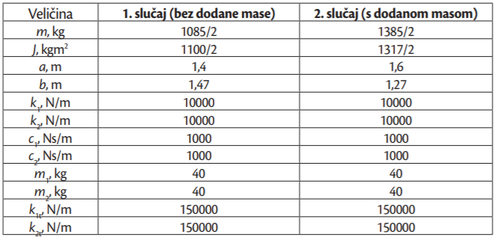
Da bi se istražio utjecaj dodavanja tereta na gibanje vozila prilikom prelaska preko umjetne izbočine provedene su dvije odvojene simulacije za koje su ulazni podaci dani utablici 1. Dimenzije umjetne izbočine preuzete su iz Pravilnika (NN 92/2019) za brzine manje od 30 km/h te iznose H = 0,07 m i L = 1,2 m (slika 3).
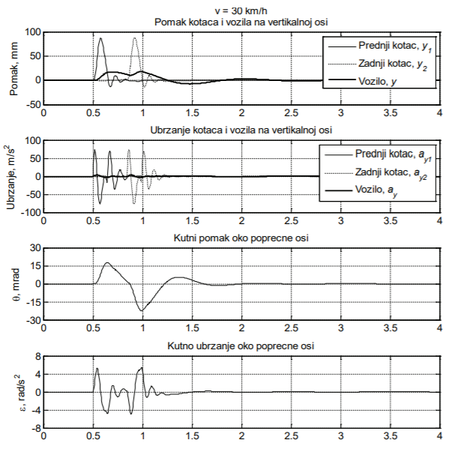
Vertikalni pomaci i ubrzanja vozila i kotača te kutni pomaci i ubrzanja vozila pri brzini vožnje 30 km/h za 1. slučaj (bez dodane mase) prikazani su naslici 6. U 1. slučaju podrazumjeva se da ovješenu masu čine polovica mase praznog vozila i vozača. Naslici 6, su primjetne dvije vršne vrijednosti vertikalnih pomaka od kojih se prva odnosi na trenutak (t = 0,58 s) prelaska prednjeg kotača, a druga vršna vrijednost na trenutak (t = 0,92 s) prelaska zadnjeg kotača preko umjetne izbočine. Vremenski razmak između navedene dvije vršne vrijednosti iznosi 0,34 s, a uvjetovano je brzinom vozila i međuosovinskim razmakom vozila. Saslike 6 vidljivo je kako su vertikalna ubrzanja prednjeg i zadnjeg kotača u oba slučaja znatno veća od vertikalnog ubrzanja vozila, što znači da je ovjes u velikoj mjeri smanjio prijenos vertikalnog ubrzanja s kotača na vozilo. Zbog relativnog međudjelovanja prvog kotača i ovješene mase tijekom prelaska prvog kotača preko umjetne izbočine pomak ima jednu vršnu vrijednost dok ubrzanje ima dvije vršne vrijednosti. Isto se događa i tijekom prelaska zadnjeg kotača preko umjetne izbočine. Praćenjem kutnih zakreta oko poprečne osi može se zaključiti da se ovješena masa nakon nailaska prednjih kotača na umjetnu izbočinu počinje uspinjati dok u trenutku nailaska zadnjeg kotača na umjetnu izbočinu ovješena masa počinje posrtati. Nakon prelaska zadnjeg kotača preko izbočine, ovješena masa doživljava još jedan puni prigušeni titraj kutnog pomaka nakon čega se vraća u početni horizontalni položaj. Što se tiče kutnog ubrzanja ovješene mase, ono slično vertikalnom ubrzanju doživljava više promjena nego odgovarajući kutni pomak, pri čemu su vršne vrijednosti vezane uz trenutak nailaska prvog, odnosno, drugog kotača na izbočinu puno intenzivnije u odnosu na druge vršne vrijednosti.
Ako se vozilu iz 1. slučaja doda teret mase 300 kg (npr. zbog ukrcaja putnika na sjedalo suvozača i na stražnje sjedalo te dodavanja tereta u prtljažniku) to će dovesti do pomaka centra mase vozila za 0,2 m prema zadnjem kraju vozila. U tom slučaju nove udaljenosti prednjeg i zadnjeg kotača od težišta vozila iznose redom: a = 1,4 + 0,2 = 1,6 m, b = 1,47 – 0,2 = 1,27 m.
Izvor: rad autora
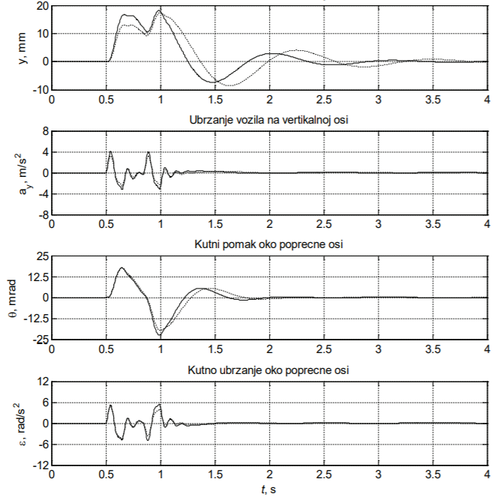
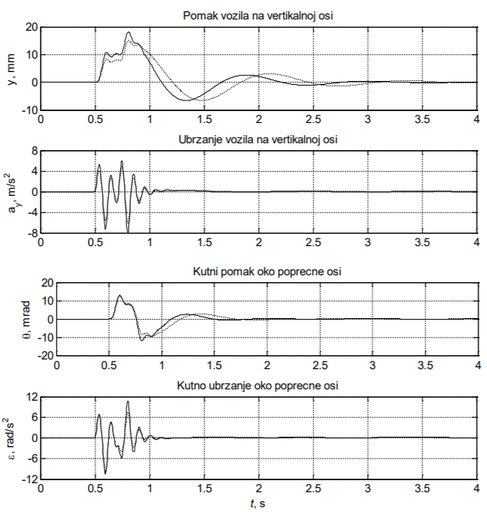
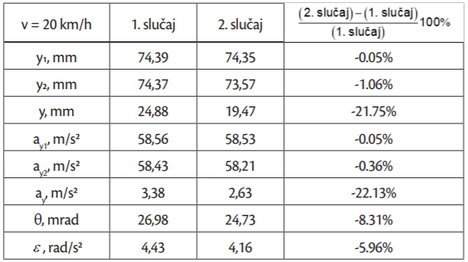
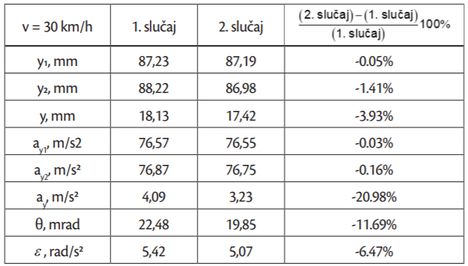
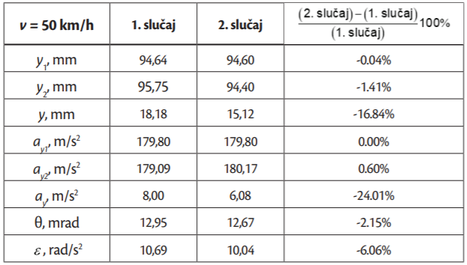
U tablicama2,33 i4 prikazana je usporedba maksimalnih apsolutnih vrijednosti promatranih veličina (vertikalnih pomaka i ubrzanja vozila i kotača te kutnih pomaka i ubrzanja vozila) u oba slučaja (bez i s teretom) pri brzinama vožnje 20 km/h, 30 km/h i 50 km/h, respektivno. Dobar uvid u utjecaj dodatnog tereta na gibanje vozila može se dobiti promatranjem postotnog odstupanja maksimalnih vrijednosti u slučaju bez i sa dodanim teretom. Najveća se odstupanja javljaju kod vertikalnih pomaka (–21.75%, –3.39%, –16.84%) i vertikalnih ubrzanja (–22.13%, –20.98%, –24.01%) vozila te kutnih pomaka (–8.31%, –11.69%, –2.15%) i kutnih ubrzanja vozila (–5.96%, –6.47%, –6.06%). To je pokazatelj učinkovitosti ovjesa, koji je u ovom slučaju gotovo u potpunosti smanjio prijenos vertikalnog gibanja s kotača na vozilo. Najveća odstupanja vertikalnih pomaka i vertikalnih ubrzanja vozila uočeni su pri brzinama vožnje za koje nije projektirana izbočina (20 km/h i 50 km/h), dok se najveći kutni pomaci i kutna ubrzanja javljaju pri brzini 30 km/h. Vremenski odzivi veličina s najizraženijim odstupanjima, odnosno, vertikalnih pomaka i ubrzanja vozila te kutnih pomaka i ubrzanja vozila, kod brzina vožnje 30 i 50 km/h, prikazani su na slikama 7 i 8, respektivno.
Izvor: rad autora
Izvor: rad autora
Izvor: rad autora
Kod brzina 20 i 50 km/h utjecaj promjene opterećenja mase vozila ima izraženije posljedice u smislu promjene vertikalnih pomaka (–21,75 %, –16,84 %) ovješene mase, y, dok se kod brzine 30 km/h uočava da promjena opterećenja vozila ima gotovo zanemariv utjecaj na vertikalne pomake ovješene mase (–3,93 %). Iz navedenoga slijedi; ako se vozilo giba sa brzinom za koji je izbočina projektirana tada promjena opterećenja vozila nema značajniji utjecaj na promjenu odziva ovješene mase. Treba napomenuti da su predmet usporedbe bile apsolutne veličine kinematičkih veličina te da kod različitih brzina vozila i različitih kinematičkih odziva ovjesa (vertikalni i kutni pomaci i ubrzanja) one mogu biti vezane ili uz trenutak prelaska prednjih ili uz trenutak prelaska zadnjih kotača preko umjetne izbočine. Osim toga, predmet usporedbe mogu biti maksimalne apsolutne vrijednosti pozitivnih ili negativnih vrijednosti. Iz toga može se zaključiti da u relativnoj usporedbi ne uspoređujemo uvijek iste pod-događaje niti iste ekstreme odziva (min, max) iz čega proizlaze i odstupanja od očekivanih intuitivnih trendova.
6. ZAKLJUČAK
U ovom radu opisan je matematički model vozila s četiri stupnja slobode gibanja te postupak modeliranja umjetne izbočine. Matematički model vozila, odnosno, diferencijalne jednadžbe gibanja vozila dobivene su primjenom 2. Newtonovog zakona. Za izabrani tip automobila, provedene su numeričke simulacije u računalnom programu Matlab/Simulink kako bi se pokazao utjecaj dodatnog tereta na gibanje vozila pri prelasku preko umjetne izbočine. Usporedbom pomaka i ubrzanja vozila i kotača u slučaju bez i s teretom kod tri brzine vožnje (20 km/h, 30 km/h i 50 km/h) pokazano je da dodavanje tereta smanjuje vertikalne i kutne pomake i ubrzanja vozila, dok nema značajnijeg utjecaja na pomake i ubrzanja kotača. To je pokazatelj učinkovitosti ovjesa, koji je u promatranom slučaju gotovo u potpunosti smanjio prijenos gibanja s kotača na vozilo.