On the New Approach to Determining Areas from Maps

On the New Approach to Determining Areas from Maps

In cartometry, a special branch of cartography, a number of different methods have been developed to determine areas from maps.Maling (1989) specifies, among other things, area determination based on simple geometric figures, by comparison with standard figures, the square method, the method of counting the nodes of a square grid, the method of measuring by going around the edge of a territory (planimetrics), the weighing method.

The invention of the digitizer in the 1960s made it possible to digitize the boundaries of a polygon whose area was to be determined. It so doing, it is necessary to transform the coordinates from the local digitizer system using identical points, e.g. the intersection of meridian lines and parallels, into the map projection system in which the map was made. From the coordinates thus obtained in the map projection, it is possible to calculate the area of the polygon on the ellipsoid, not only from the equivalent but also from other projections if the projection distortions are eliminated (Frančula et al. 1993,Frančula et al. 2021).Gillissen (1993) andvan Gein and Gillissen (1993) propose that in calculating the areas of geodetic polygons along geodetic lines, interpoints be interpolated and that all points of the geodetic polygon be mapped to Albers' equal area conic projection. If the sides of the geodetic polygon are short enough (e.g. 100 m or 200 m), it can be considered that all geodetic lines have been mapped as line segments so that the area can be calculated in the Albers projection.

Pędzich and Kuzma (2012) believe that the best solution for calculating the area of geodetic polygons with short sides is to map all points of boundary polygons from an ellipsoid into an equal area projection and calculate the area in that projection. For calculating the areas of the five largest administrative units in Poland, they map all the points of the boundary polygons into Witkowski’s equal area conic projection. The mean length of the sides was between 45 m and 75 m. In addition to this procedure, they calculated the areas of administrative units, among other things, according to the formulas proposed byKarney (2011). The maximum area difference obtained by these two methods is 0.195 ha. A comparison with data from Polish statistical yearbooks, given with an accuracy of 1 ha, gives differences of several hectares. Data from statistical yearbooks were obtained by digitization from topographic maps at a scale of 1 : 10,000, so the authors believe that the areas of the polygons were calculated with greater accuracy.

Figure 1. Determining the area of a geodetic polygon in the middle of the map / Sl. 1 Određivanje površine geodetskog poligona u sredini karte

Figure 2. Determining the area of a geodetic polygon near the edge of the map /Sl. 2 Određivanje površine geodetskog poligona blizu ruba karte

Danielsen (1993),Sjöberg (2006) andKarney (2013) derived formulas for calculating the areas of geodetic polygons, i.e. polygons whose sides are geodetic lines, on an ellipsoid without mapping that polygon into the plane of a map projection.

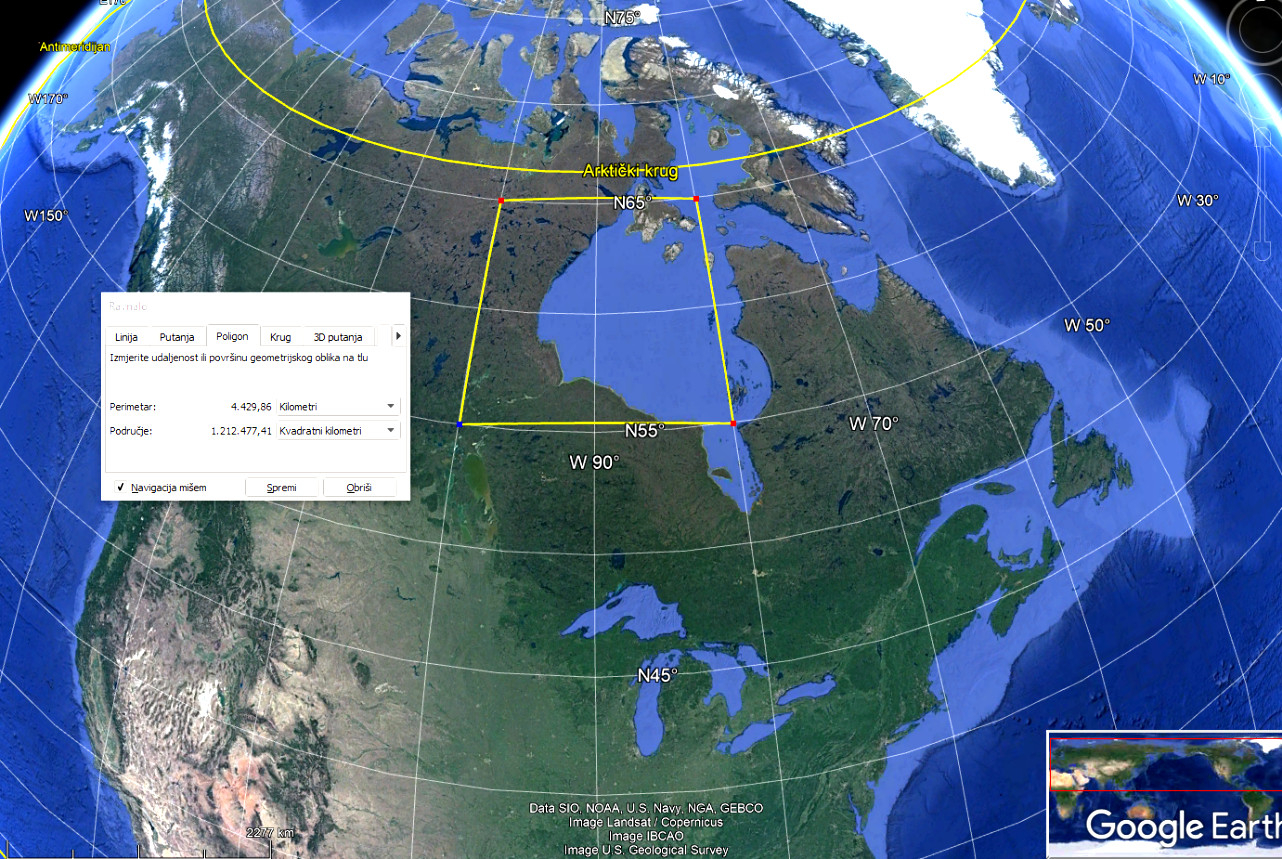
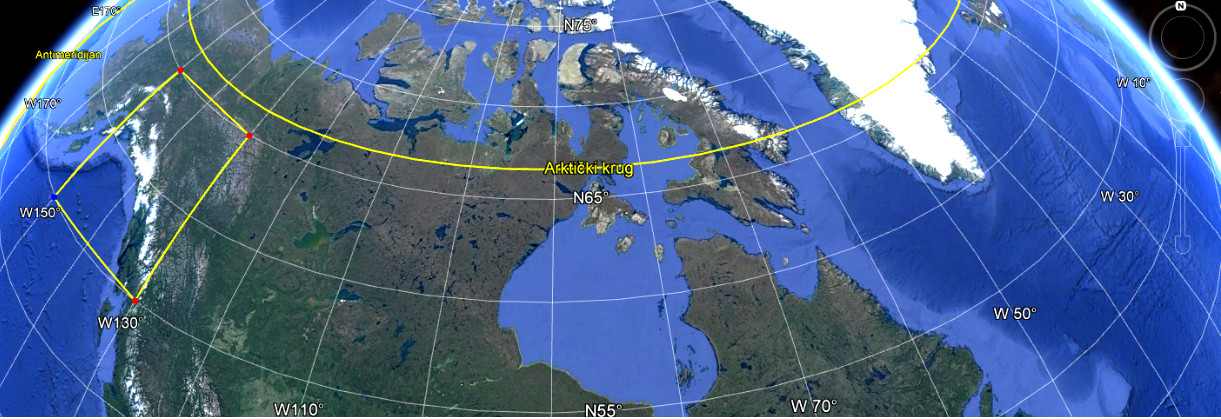
In 2005, Google launched Google Maps and Google Earth. Both of these services have tools for measuring lengths and areas. By measuring with these tools, the lengths and areas on the ellipsoid will be obtained, i.e. free from projection distortions (Frančula 2020). Figures1 and2 illustrate that the length of the sides of a geodetic polygon does not have to be taken into account in Google Earth. The images show geodetic polygons with sides approximately 1000 km long. If the polygon inFig. 2 is compared with the same polygon in the middle of the map (Fig. 1), a large distortion of the areas is visible. 1 212 477 km ² were obtained as the area of the geodetic polygon inFig. 1, and 1 201 210 km ² for the area of the same geodetic polygon inFig. 2. The difference is 11,267 km ² or 0.9%, which is the result of measurement errors.

Some GIS software (QGIS, ArcGIS Online, Global Mapper) also have the ability to determine areas on an ellipsoid (Frančula et al. 2021). We do not know how the specified services and programs calculate the areas. Their authors and manufacturers do not provide information about this in their user manuals. It is our opinion that it is most acceptable to calculate the geodetic coordinates φ and λ on the ellipsoid from the coordinates x, y in the applied map projection and then according to some of the known formulas, e.g. Sjöberg (Sjöberg 2006), to calculate the area on an ellipsoid. Such an approach is particularly suitable for GIS software that allows the determination of map areas in many map projections. If our assumption is correct, this is a novelty in relation to previous procedures in which all calculations were performed in the plane, seeFrančula et al. (1993).

O novom pristupu određivanju površina s karata

U kartometriji, posebnoj grani kartografije, razvijen je niz različitih metoda za određivanje površina s karata.Maling (1989) navodi, među ostalim, i određivanje površine na temelju jednostavnih geometrijskih likova, usporedbom sa standardnim likovima, metodom kvadrata, metodom brojenja čvorova kvadratne mreže, metodom mjerenja obilaženjem ruba teritorija (planimetriranje), metodom vaganja.

Izum digitalizatora 1960-ih omogućio je da se granica poligona čiju površinu treba odrediti digitalizira. Pritom je potrebno koordinate iz lokalnog sustava digitalizatora s pomoću identičnih točaka, npr. presjeka linija meridijana i paralela, transformirati u sustav kartografske projekcije u kojoj je karta izrađena. Iz tako dobivenih koordinata u projekciji moguće je izračunati površinu poligona na elipsoidu, ne samo iz ekvivalentnih nego i ostalih projekcija ako se pri tome eliminiraju deformacije projekcije (Frančula i dr. 1993,Frančula i dr. 2021).

Gillissen (1993) tevan Gein i Gillissen (1993) predlažu da se u računanju površina geodetskih poligona uzduž geodetskih linija interpoliraju međutočke i da se potom sve točke geodetskog poligona preslikaju u Albersovu ekvivalentnu konusnu projekciju. Ako su stranice geodetskog poligona dovoljno kratke (npr. 100 m ili 200 m), može se smatrati da su se sve geodetske linije preslikale kao dužine pa se površina može računati u Albersovoj projekciji.

Pędzich i Kuzma (2012) smatraju da je za računanje površina geodetskih poligona s kratkim stranicama najbolje rješenje preslikavanje svih točaka graničnih poligona s elipsoida u neku ekvivalentnu projekciju i računanje površine u toj projekciji. Oni za računanje površina pet većih administrativih jedinica u Poljskoj sve točke graničnih poligona preslikavaju u ekvivalentnu konusnu projekciju Vitkovskog. Srednja duljina stranica bila je između 45 m i 75 m. Osim tim postupkom izračunali su površine administrativnih jedinica, među ostalim, i po formulama koje je predložioKarney (2011). Maksimalna razlika površina dobivena tim dvjema metodama je 0,195 ha. Usporedba s podatcima iz poljskih statističkih godišnjaka, danih s preciznošću od 1 ha, daje razlike od nekoliko hektara. Podatci iz statističkih godišnjaka dobiveni su digitalizacijom s topografskih karata mjerila 1 : 10 000 pa autori smatraju da su površine poligona izračunali s većom točnošću.

Danielsen (1993),Sjöberg (2006)iKarney (2013) izveli su formule za računanja površina geodetskih poligona, tj. poligona čije su stranice geodetske linije, na elipsoidu bez preslikavanja tog poligona u ravninu neke kartografske projekcije.

Google je 2005. pokrenuo Google Maps i Google Earth. Obje te usluge imaju alate za mjerenje duljina i površina. Mjereći tim alatima dobit će se duljine i površine na elipsoidu, dakle oslobođene deformacija projekcije (Frančula 2020). Da se u Google Earth ne mora voditi računa o duljini stranica geodetskog poligona ilustriramo sa slikama1 i2. Na slikama su geodetski poligoni sa stranicama duljina oko 1000 km. Ako se poligon nasl .2 usporedi s jednakim poligonom u sredini karte (slika 1) vidljiva je velika deformacija površina. Za površinu geodetskog poligona nasl. 1dobiveno je 1 212 477 km², a 1 201 210 km² za površinu jednakog geodetskog poligona nasl. 2. Razlika je 11 267 km² ili 0,9 %, što je rezultat pogrešaka mjerenja.

I neki GIS softveri (QGIS, ArcGIS Online, Global Mapper) imaju mogućnost određivanja površina na elipsoidu (Frančula i dr. 2021). Ne znamo na koji način navedene usluge i programi računaju površine. Njihovi autori i proizvođači u uputama za upotrebu ne daju o tome informacije. Naše je mišljenje da je najprihvatljivije iz koordinata x, y u primijenjenoj kartografskoj projekciji izračunati geodetske koordinate φ i λ na elipsoidu i potom po nekim od poznatih formula, npr. Sjöbergovim (Sjöberg 2006), izračunati površinu na elipsoidu. Takav pristup naročito je prikladan za GIS softvere koji omogućuju određivanje površina s karata u mnogim kartografskim projekcijama. Ako je ta naša pretpostavka točna, to je novina u odnosu na dosadašnje postupke u kojima su se sva računanja obavljala u ravnini, vidi npr.Frančula i dr. (1993).