INTRODUCTION
The contribution of this article is study of two different control strategies for a class of chemical process industries. The model of the distillation column used in this plant, which is characterized by an underactuated structure. According to the diversity and complexity of these systems, it is important to emphasize that none of the technique proposed and developed for fully actuated systems can be applied directly to any underactuated system. Therefore, it is meaningful to develop control methods for this class of systems, and more precisely to develop the most optimized controller design. The control objective for systems characterized by the fact that there are more degrees of freedom than actuators, is to obtain a desirable behavior of several output variables by simultaneously manipulating several inputs channels. Under-actuated systems are less sensitive to modelling errors, so it has to be controlled in its original form to obtain robust stability and performance[1]. Garcia and Morari (1985), and Morari and Zafirious (1989) presented the concept of Internal Model Control (IMC) and have already proved the effectiveness of the framework for robust control of different kinds of Singular-Input Singular Output (SISO) systems. The IMC structure is composed of three principal parts: the process, the internal model in parallel to the process and the controller, which is the dynamic inversion of the model[2]. Recently, many methods have been proposed to control MIMO systems with time delays. For example, Xianku and Hongshuai (2015) proposed a Closed-loop Gain Shaping Algorithm (CGSA) using Padé approximation, which is sufficiently accurate in view of stability analysis[3]. Qibing, Beiyan, Qi and Guanfei (2014) introduced a design method of decoupling internal model control; the basic idea is to realize the decoupling of the controller of non-square processes by inserting some compensation Relative Normalized Gain Array (RNGA). An equivalent transfer function matrix is introduced to approximate the pseudo-inverse of the process transfer function matrix, which makes the design of decoupling internal model control simple and easy to calculate[4]. Guanfei and Qi (2013) integrated IMC with disturbance controllers by choosing different forms of external input/output disturbance. When this disturbance is applied directly as input to the controller, the design of controller needs to compensate the effect of slow dynamic poles by adding some constraints[5]. Pamela, Jebarajan and Baby introduced an approach to regulate the heater power in those systems, which must control the temperature in food processing, pharmaceuticals and in polymerization. The objective is to control the system with both PI controller and IMC structure and to analyze its performance parameters[6]. Qi, Laing, Feng and Si-wen (2012) proposed a novel design IMC controller based on Singular Value Decomposition (SVD), this approach uses SVD in the inverse of the steady-state gain matrix of process[7]. The last decades have shown an increasing interest in the control of under-actuated systems, many IMC methods can be introduced to achieve considerable results on the control for these kinds of systems. For this class of system, the number of inputs is smaller than the number of outputs, which means that the transfer function matrix is not square, and the issue of inversion exists. As a result, the problem of inversion was solved in many literature researches previously mentioned[4-6] by decoupling the internal model control based on the Relative Normalized Gain Array (RNGA), Singular Value Decomposition (SVD) and an Equivalent Transfer Function (ETF) matrix. The solution brought by these methods require complicated calculations and many instructions to implement[7]. Otherwise, our proposed approach; Virtual Inputs is used to augment the system inputs inserting a certain number of virtual columns to the model in order to make it a square matrix. These virtual columns have no influence on the response of the system, and they will be eliminated after. The control of under-actuated systems is challenging, hence the necessity to identify the control technique with less interactions and better performances such as overshoot, setting time etc. Based on internal model control for discrete under-actuated systems a comparison based on the inversion technique of the model will be made between Singular Value Decomposition (SVD) and Virtual Inputs (VI) to realize the internal model controller. In this article, section 2 summarizes the fundamental control problem to be solved. Section 3 describe the general IMC structure. Section 4 details the design of the internal controller based on Singular Value Decomposition. Section 5 details the design of the internal controller based on Virtual Inputs. At the end, we show how our proposed methodology based on Virtual Inputs at distillation column could give good results compared to the other method described previously.
PROBLEM FORMULATION
The process to be controlled is assumed linear and discrete-time governed by the following equation[8]
Wheren x Î ℝn i is the system state, u Î ℝm is the vector of manipulated variables, y Î ℝ n is the vector of system outputs, is the time delays, F, H and C are matrices of corresponding dimensions[8]. For the IMC design technique, it is convenient to express this model in frequency response form. Taking Z transforms of (1), the following input-output model is obtained:
Where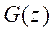 is the system transfer
matrix of dimension
is the system transfer
matrix of dimension  , the number
of control inputs is equal to m, the number of outputs is equal to n, making it a
rectangular matrix, which has the form
, the number
of control inputs is equal to m, the number of outputs is equal to n, making it a
rectangular matrix, which has the form
 , are
the transfer functions of z and
, are
the transfer functions of z and 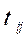 is the delay in the response of output i to input j. The synthesis of an IMC
controller that is equal to the inverse of the model expression and is fundamental
to ensure perfect set-point tracking and this represents the basic problem of the
IMC approach. In fact, the realization of the direct model inverse is difficult, and
sometimes not possible to realize, for many physical systems[89]. This perfect
controller cannot be implemented for the following reasons.
is the delay in the response of output i to input j. The synthesis of an IMC
controller that is equal to the inverse of the model expression and is fundamental
to ensure perfect set-point tracking and this represents the basic problem of the
IMC approach. In fact, the realization of the direct model inverse is difficult, and
sometimes not possible to realize, for many physical systems[89]. This perfect
controller cannot be implemented for the following reasons. (i) If the model contains time delays, its inverse involves predictive terms, which make the controller unrealizable.
(ii) If the zeros of the transfer matrix of the model outside the complex unit circle yield an unstable perfect controller.
(iii) System equipped with a perfect controller is extremely sensitive to modelling errors and time delays.
(iv) The direct model inversion is also impossible in the case of underactuated systems.
In fact, the model must provide an accurate description of the process dynamics and characteristics. Therefore, the model expression must be very close to that of the plant. For underactuated systems, the number of control inputs is less than the number of outputs and therefore we will have a rectangular matrix that is invertible. This represents the major problem encountered. In this article, to resolve this problem, it is proposed to develop some methods of inversion in the case of under-actuated systems.
INTERNAL MODEL CONTROL DESCRIPTION
The development of the IMC structure has progressed in recent years in order to design an optimal feedback controller. In this section we present the general IMC structure and we describe its basic principles and properties. Due to the fact that the traditional IMC methods cannot solve the control problem of non-square systems, we introduce two design technique to realize the internal controller but, when using a matrix to describe a non-square system, the issue of inversion often emerges.
THE GENERAL IMC DESCRIPTION
The general IMC structure of multivariable systems adopted in this article is shown
in Figure 1, where  ,
,
 and
and 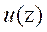 are the output vector of the process, the
output of internal model and the control variable, respectively. r(z) is the
set-point vector, d(z) is the disturbance,
are the output vector of the process, the
output of internal model and the control variable, respectively. r(z) is the
set-point vector, d(z) is the disturbance, and
and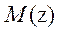 represent the transfer function matrix of
process and its model,
represent the transfer function matrix of
process and its model, 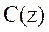 is the
transfer matrix of the IMC controller.
is the
transfer matrix of the IMC controller.
We begin by reviewing the properties of the IMC structure. This structure is equivalent to a conventional feedback loop with controller. From Figure 1 the inputs vector u(z) and the system outputs vector y(z) are expressed by
Property 1. Dual Stability; Assuming an ideal model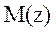 =
=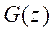 and
and 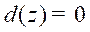 , stability of both the
controller
, stability of both the
controller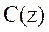 and the
process
and the
process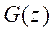 is then sufficient
for overall system. Then equations (4) and (5) becomes: Therefore, the system poles as well as the controller poles must lie inside
the unit circle (UC) for stability. On the other hand, when
is then sufficient
for overall system. Then equations (4) and (5) becomes: Therefore, the system poles as well as the controller poles must lie inside
the unit circle (UC) for stability. On the other hand, when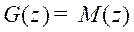 the stability is not affected by adding
constraints on the inputs.
the stability is not affected by adding
constraints on the inputs. Property 2. Perfect Control; Assume that the controller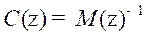 , yields a closed-loop stable IMC loop, this
controller is equivalent to the inverse model to achieves perfect set-point
satisfaction despite any disturbance. Furthermore,
, yields a closed-loop stable IMC loop, this
controller is equivalent to the inverse model to achieves perfect set-point
satisfaction despite any disturbance. Furthermore,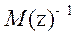 is often not realizable.
When
is often not realizable.
When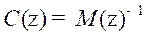 is verified, transfer
function (7) becomes
is verified, transfer
function (7) becomes
Property 3. Zero Offset; Assume that the steady state gain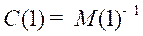 controller is equal to the inverse model
gain and the closed-loop system in Figure 1 is stable. The key to apply the IMC
structure is the controller who would yield the best output response possible.
However, as in the under-actuated case, this perfect controller cannot be
implemented for previous reasons. We will discuss in the next section the controller
design using two different methods; Singular Value Decomposition (SVD) and Virtual
Input (VI). These methods are based on the transfer function matrix of the model of
the process.
controller is equal to the inverse model
gain and the closed-loop system in Figure 1 is stable. The key to apply the IMC
structure is the controller who would yield the best output response possible.
However, as in the under-actuated case, this perfect controller cannot be
implemented for previous reasons. We will discuss in the next section the controller
design using two different methods; Singular Value Decomposition (SVD) and Virtual
Input (VI). These methods are based on the transfer function matrix of the model of
the process.
IMC STRUCTURE BASED ON SINGULAR VALUE DECOMPOSITION
The application of the internal model structure to under-actuated systems is considered like our main target. In this section, we will describe the design phase of the internal controller based on SVD and the implementation at the level of the structure IMC. This approach of design can realize the decoupling of under-actuated processes and eliminate the unrealizable factors by inserting compensated terms. Meanwhile, a non-diagonal filter is designed based on SVD matrix theory. We discuss with more details this approach in the following.
The IMC structure of an under-actuated systems based on SVD is shown in Figure 2, where CSVD(z) is the IMC controller.
IMC structure based on SVD method. The SVD of the transfer matrix G(z) of the under-actuated systems is as follows: Where,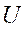 is
an
is
an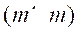 orthonormal matrix
and
orthonormal matrix
and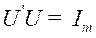 ,
, 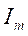 ( is the identity matrix),
( is the identity matrix),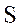 is an diagonal matrix with singular values
of
is an diagonal matrix with singular values
of in the
diagonal,
in the
diagonal,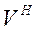 is
an
is
an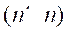 orthonormal matrix
and
orthonormal matrix
and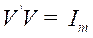 and
and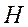 represented the conjugate transpose. The
SVD is essentially trying to reduce the rank of the matrix and to approximate them
as a linear combination[10]. The closed loop transfer function matrix deduced from
Figure 2 is given by: where
represented the conjugate transpose. The
SVD is essentially trying to reduce the rank of the matrix and to approximate them
as a linear combination[10]. The closed loop transfer function matrix deduced from
Figure 2 is given by: where 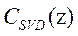 is a non-square
internal model controller based on Singular Value Decomposition has two main roles;
on one hand make the internal control, while compensating and decoupling the system
to reduce coupling between channels and, on the other hand, it can satisfy the
robustness and the performances of the systems. The design method of the
under-actuated internal model controller
is a non-square
internal model controller based on Singular Value Decomposition has two main roles;
on one hand make the internal control, while compensating and decoupling the system
to reduce coupling between channels and, on the other hand, it can satisfy the
robustness and the performances of the systems. The design method of the
under-actuated internal model controller 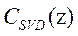 is given below.
is given below. In the nominal case, 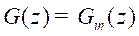 equation
(10) becomes
equation
(10) becomes
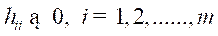 . Hence, in the
traditional IMC structure[11], the closed loop transfer function
. Hence, in the
traditional IMC structure[11], the closed loop transfer function and the general decoupled internal model
controller
and the general decoupled internal model
controller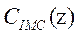 should be
respectively
should be
respectivelyIt is obvious that once
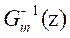 and
and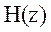 are specified, it is
possible to determine
are specified, it is
possible to determine 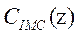 . We start
by finding the
. We start
by finding the 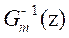 but in
under-actuated systems; the exact inverse of the model does not exist, so we replace
it with the generalized inverse of
but in
under-actuated systems; the exact inverse of the model does not exist, so we replace
it with the generalized inverse of 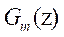 [12]. Hence, the result of this inversion is
the unit matrix
[12]. Hence, the result of this inversion is
the unit matrix 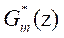 :Where
:Where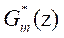 and
and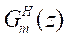 are the pseudo-inverse and the Hermitian
matrix of
are the pseudo-inverse and the Hermitian
matrix of 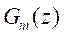 respectively. The
expression (13) becomes Next, we choose the appropriate
respectively. The
expression (13) becomes Next, we choose the appropriate 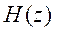 . Whereas the model
. Whereas the model 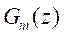 consists into two parts to handle many
limitations in this technique Where
consists into two parts to handle many
limitations in this technique Where 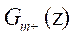 contains time
delays and zeros of
contains time
delays and zeros of 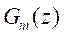 outside the
unit circle such
outside the
unit circle such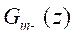 has a stable
and realizable inverse. In the traditional internal model controller design[12],
adding the filter is used to supplement the model mismatch and ignore the error
caused by the non-minimum phase portion, as shown in equation (17). Substituting equations (16) and (17) into equation (12) leads to: Where
has a stable
and realizable inverse. In the traditional internal model controller design[12],
adding the filter is used to supplement the model mismatch and ignore the error
caused by the non-minimum phase portion, as shown in equation (17). Substituting equations (16) and (17) into equation (12) leads to: Where 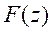 is a designed
filter of internal model controller. It can be considered as the general form[13]:Among them: In the above formula,
is a designed
filter of internal model controller. It can be considered as the general form[13]:Among them: In the above formula,  is
the time constant of the design filter, it determines the bandwidth of the
closed-loop system and thus serves as a tuning parameters for performance and
robustness,
is
the time constant of the design filter, it determines the bandwidth of the
closed-loop system and thus serves as a tuning parameters for performance and
robustness, 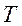 is the sampling time
of the system. Furthermore, when the high performance is required,
is the sampling time
of the system. Furthermore, when the high performance is required, but it is intuitively obvious that this
choice makes the system very sensitive and it can very easily become unstable even
for small modeling errors. In addition, the completely decoupling can be obtained by
choosing
but it is intuitively obvious that this
choice makes the system very sensitive and it can very easily become unstable even
for small modeling errors. In addition, the completely decoupling can be obtained by
choosing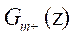 and
and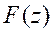 diagonal. Even when dynamic interactions
are allowed,
diagonal. Even when dynamic interactions
are allowed,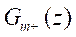 and
and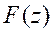 must satisfy[13]: In the following discussion, we give procedures for finding
must satisfy[13]: In the following discussion, we give procedures for finding 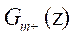 and a rule for filter design. Assume
and a rule for filter design. Assume
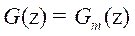 , and that
, and that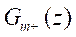 is diagonal with the following form[14] where
is diagonal with the following form[14] where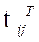 is the maximum
prediction in the i-th row of
is the maximum
prediction in the i-th row of 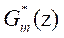 ,
,
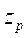 is the pole in outside of
the unit circle,
is the pole in outside of
the unit circle,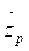 is the
conjugate complex of
is the
conjugate complex of 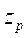 ,
,
 represents the maximum
number of the same pole of
represents the maximum
number of the same pole of 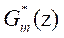 .
IMPROVEMENT OF FILTER
.
IMPROVEMENT OF FILTERAccording to the equation (17), the robustness of the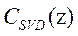 often cannot meet the requirement, for
solving this problem, this approach need to improve the filter F(z). The filtering
structure is designed in general, which makes control system bear the capacity of
high-dimensional decoupling and fast response. First, we use the SVD in the inverse
of the transfer functions matrix of process
often cannot meet the requirement, for
solving this problem, this approach need to improve the filter F(z). The filtering
structure is designed in general, which makes control system bear the capacity of
high-dimensional decoupling and fast response. First, we use the SVD in the inverse
of the transfer functions matrix of process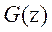 . Then, we can use the term after
decomposition to improve the filter
. Then, we can use the term after
decomposition to improve the filter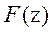 and to obtain the controller based on
SVD.
and to obtain the controller based on
SVD.
Step 1: Use the SDV in the inverse of the steady-state gain matrix of 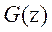
Step 2: Let 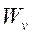 satisfy the following
formula
satisfy the following
formula
Step 3: The improved internal model controller is as follows
The robustness of the system can be greatly enhanced by adding a
filter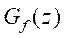 in the feedback loop,
and the filter time constant can be set to half of the maximum delay time in this
loop[15].
in the feedback loop,
and the filter time constant can be set to half of the maximum delay time in this
loop[15].
IMC STRUCTURE BASED ON VIRTUAL INPUTS (VI)
Focusing now on the inversion method of the under-actuated systems based on Virtual Inputs. To successfully apply our approach, firstly we need to modify the IMC basic structure mentioned in Figure 1, so that it becomes applicable to underactuated systems with more outputs than control inputs. Secondly, we design an approximate inverse of the model plant which is inspired by the studies of[16,17] in the case of MIMO systems and over-actuated systems[18].
The modified IMC structure presented in Figure 3 is characterized by two more blocks with respect to the basic IMC structure presented in Figure 1[19]. The first new block is the Virtual Inputs Augmentation VIA (z) which is used to augment the system inputs inserting virtual column to the transfer
matrix of the non-square system in order to make it of dimension
column to the transfer
matrix of the non-square system in order to make it of dimension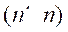 , so that it can be inverted. The second
one is the Virtual Inputs Removing VIR (z) block which is used to eliminate the
exceeding virtual inputs[19].
, so that it can be inverted. The second
one is the Virtual Inputs Removing VIR (z) block which is used to eliminate the
exceeding virtual inputs[19]. The inserting columns mentioned previously can be chosen as first-order transfer functions, which verify the stability criterion, and in order to simplify the study and avoid inversion problems[19]. The studied system can be shown through the following equation[18, 19]:
When the model and the system match perfectly , the augmented system
, the augmented system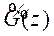 and its exact model are expressed as: The Virtual Inputs Controller CVIN (z) design presented in Figure 4 is based
on the inversion method reported in[18, 19]. The closed-loop transfer function matrix CVIN (z) between e(z) and u(z) is
derived as: Where
and its exact model are expressed as: The Virtual Inputs Controller CVIN (z) design presented in Figure 4 is based
on the inversion method reported in[18, 19]. The closed-loop transfer function matrix CVIN (z) between e(z) and u(z) is
derived as: Where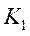 is an invertible
square matrix
is an invertible
square matrix  used to ensure the
stability of the controller and it can be expressed by
used to ensure the
stability of the controller and it can be expressed by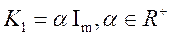 , a second gain
, a second gain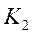 is introduced as reported in Figure 4 in
order to compensate the static errors. The gain
is introduced as reported in Figure 4 in
order to compensate the static errors. The gain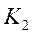 is given by equation (30). For sufficiently high values of
is given by equation (30). For sufficiently high values of 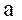 , the controller CVIN(z) approaches the
inverse of internal model
, the controller CVIN(z) approaches the
inverse of internal model  : For the construction of the controller, it is necessary to respect the fact
that:The virtual inputs method proposed for the design of the controller by
internal model is valid whatever the number of outputs
: For the construction of the controller, it is necessary to respect the fact
that:The virtual inputs method proposed for the design of the controller by
internal model is valid whatever the number of outputs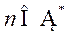 and inputs
and inputs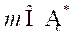 of a physical system. In fact, this
approach is applicable for the following classes of systems:
of a physical system. In fact, this
approach is applicable for the following classes of systems: - Monovariable system where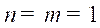
- Overactuated system where 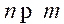
- Underactuated system where 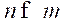
SIMULATION RESULTS AND COMPARISON
To analyze the comparative study on the above control technique, we considered a chemical process industry. In order to test the control effect of discrete underactuated internal model controller based on SVD and VI, a side-stream distillation control problem suggested by Doukas and Lyben will be used[20].
Figure 5 shows the side-stream distillation scheme that serves to separate benzene, toluene and xylene. The problem posed in this case was to control the concentrations of four impurities in three product streams with only three manipulated variables: reboiler duty, reflux ratio and side stream flow rate.
Doukas and Lyben[20] treated the distillation column as a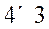 system. An internal controller should be
design for the under-actuated system. Doukas and Lyben model can be represented as Where the toluene in bottom (y1), toluene in bottom (y2), benzene in side
draw (y3) and benzene in side draw (y4) are the four controlled variables. The
reboiler duty (u1), reflux ratio (u2) and side draw (u3) are the manipulated
variables[20]. The
system. An internal controller should be
design for the under-actuated system. Doukas and Lyben model can be represented as Where the toluene in bottom (y1), toluene in bottom (y2), benzene in side
draw (y3) and benzene in side draw (y4) are the four controlled variables. The
reboiler duty (u1), reflux ratio (u2) and side draw (u3) are the manipulated
variables[20]. The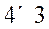 transfer
function matrix presented in equation (33) as follows
transfer
function matrix presented in equation (33) as follows
In this section, we evaluate the controller performance using the above-mentioned approach.
SIMULATION RESULTS USING THE SVD CONTROLLER
Starting with the internal controller based on Singular Value Decomposition, and
using the whole approach seen in section 4. Using equation (23), 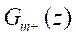 can be obtained by
can be obtained by
Using equation (24), is given as follows
is given as follows
Using equation (25),
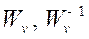 are
given as follows Considering the realization of the controller, the added
filter
are
given as follows Considering the realization of the controller, the added
filter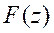 is In order to increase the robustness of system, we add a feedback filter in
feedback loop. The expression of the added filter is as follow: where,
is In order to increase the robustness of system, we add a feedback filter in
feedback loop. The expression of the added filter is as follow: where,The expression of the inverse of
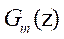 ,
,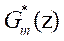 is given as follows where,
is given as follows where,
The final expression of the internal controller based on SVD described by the equation (26) is the following
SIMULATION RESULTS USING THE VIRTUAL INPUT CONTROLLER
Dealing now with our proposed approach, the Virtual Input methods applied on the same
system studied previously. Considering the same underactuated system with three
control and four outputs. The system transfer matrix G(z) is given by (33). Let us
consider the case of perfect modeling 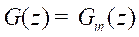 , The augmented model transfer function is
of dimension
, The augmented model transfer function is
of dimension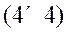 . The system and
the model outputs are expressed respectively by (58) and (59).
. The system and
the model outputs are expressed respectively by (58) and (59).
The model transfer functions
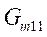 until
until are successively chosen to be close
to
are successively chosen to be close
to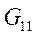 until G43. The
augmenting
until G43. The
augmenting 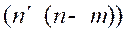 virtual column
virtual column
 ,
,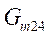 ,
, 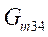 and
and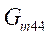 are chosen as first order transfer
functions so that they ensure the invertibility conditions of the
matrix
are chosen as first order transfer
functions so that they ensure the invertibility conditions of the
matrix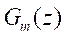 . It’s mandatory to
study the discrete-time internal controller stability, in order to set the stability
interval of the gain matrix
. It’s mandatory to
study the discrete-time internal controller stability, in order to set the stability
interval of the gain matrix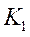 which ensures the stability of the IMC structure. The expression of the controller
(29) detailed in the previous section can be reformulated using the representation
of sate as: Where
which ensures the stability of the IMC structure. The expression of the controller
(29) detailed in the previous section can be reformulated using the representation
of sate as: Where 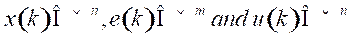 , are the state,
input and output vectors respectively of the controller, the matrices F, H and C are
known constant matrices. The stability condition highlighted by Lyapunov theory
allows to assess the necessary and sufficient condition of the controller stability.
Using this theory, we can conclude that the system presented by the equation (60) is
stable if and only if there exists a positive definite matrix
, are the state,
input and output vectors respectively of the controller, the matrices F, H and C are
known constant matrices. The stability condition highlighted by Lyapunov theory
allows to assess the necessary and sufficient condition of the controller stability.
Using this theory, we can conclude that the system presented by the equation (60) is
stable if and only if there exists a positive definite matrix 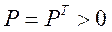 , satisfying the following Lyapunov
inequality[21]: Solving the LMI equation (61), the interval of the gain
, satisfying the following Lyapunov
inequality[21]: Solving the LMI equation (61), the interval of the gain 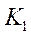 which assures the stability of the internal
controller is
which assures the stability of the internal
controller is 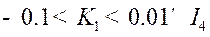 . In the case of
this system, we choose
. In the case of
this system, we choose  such
that
such
that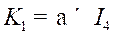 .
. The gain matrix 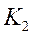 relative to
relative to
 is given by:
is given by:
COMPARISON ANALYSIS
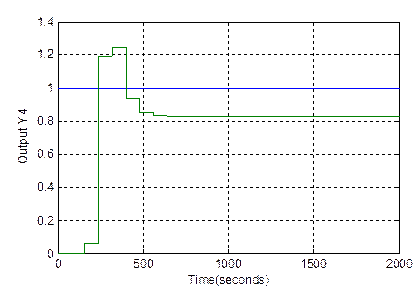
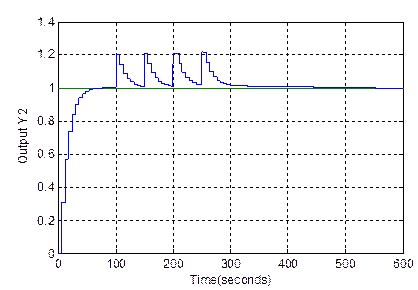
After using both Singular Value Decomposition and Virtual Inputs approaches, it seems to be quite interesting making a comparison between them showing their effectiveness in terms of stability, robustness, precision and tracking signal. From the data presented in table 1, it is relevant to note that the desired specifications of the closed-loop responses are not met with the SDV controller and this is expected because of the problem of the interaction which are too strange as illustrated by the decoupling of the controller and the simulation results obtained with the SVD controller in Figure 6. SVD method has a problem if we do not make the right choice of the parameter of the filter, in this case, the approximation cannot be made with effectiveness and the system can be diverging. Added to that this approach towards the under-actuated process is to square the system by make the decoupling of the model affecting the characteristic of the system. Unfortunately, this operation can decrease the performance of the system and making it so poor by neglecting some information’s.
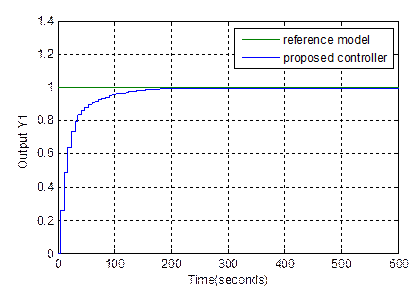
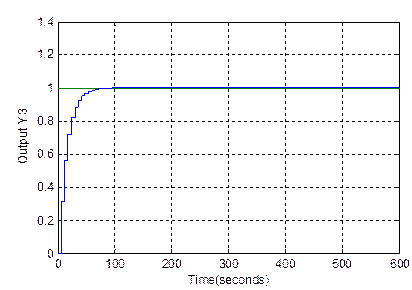
The internal model controller using a Virtual Inputs as inversion approach of the
model , better performances
in terms of rise time, settling time and in terms of error dynamics precision are
obtained, as shown by table1, these results are satisfactory because the steady
state is zero for all responses as shown in Figure 7. This mean that the set-point
tracking is ensured. The internal model control using the Virtual Input approach is
having the benefits of small overshoot, faster tracking features, and less
interaction compared to the Singular Value Decomposition method as indicated by the
Figures 6 and 7 and by the table below. The Virtual Input method may be fails when
the system has a disturbance acting on the outputs of the system. For this reason,
with load disturbance the response needs to be controlled to attain robustness and
performance.
, better performances
in terms of rise time, settling time and in terms of error dynamics precision are
obtained, as shown by table1, these results are satisfactory because the steady
state is zero for all responses as shown in Figure 7. This mean that the set-point
tracking is ensured. The internal model control using the Virtual Input approach is
having the benefits of small overshoot, faster tracking features, and less
interaction compared to the Singular Value Decomposition method as indicated by the
Figures 6 and 7 and by the table below. The Virtual Input method may be fails when
the system has a disturbance acting on the outputs of the system. For this reason,
with load disturbance the response needs to be controlled to attain robustness and
performance.
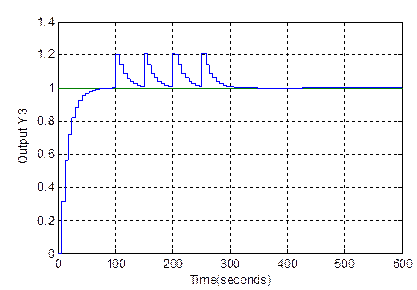
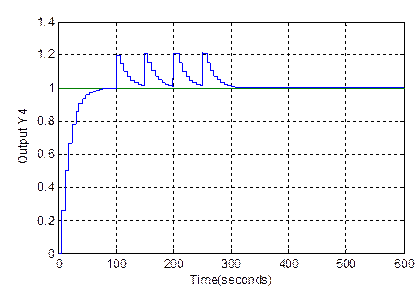
In order to verify the robustness of the proposed internal model controller, we added a white noise with a variation of 0,2 acting on the outputs of the system in the interval of time [100s, 150s, 200, 250s]. The influence of this noise is observed in Figure 8.
It is shown that the closed loop system is not sensitive to noise. We conclude that the method it offers strong robustness in case of the given perturbation and good tracking features.CONCLUSION
To control an under-actuated industrial process demands not only to know all the characteristic of his model, but also to achieve the desired performance when there exist load disturbances. Both Virtual Input and SVD approaches are applied to distillation column process, to prove the controller achievability for this industrial process and that it is the most efficient approach in terms of rapid response, set-point tracking and disturbance rejection. Through a comparative analysis, the Virtual Inputs approach avoids the complex calculation, such as calculate the inverse of the matrix, the controller structure is simple, has a few tuning parameters, and is easy to be accepted by operators. The simulation results show that our proposed method (Virtual Inputs) ensures suitably the set-point tracking and the disturbance rejection for the external disturbance as illustrated in distillation control problem suggested by Doukas and Lyben and gives better results compared to SVD approach. The modified internal model control scheme gives more degree of freedom in the controller design technique in order to improve the performance of the controlled system. As future works, it will be interesting to handle with unstable multivariable non-square systems and non-linear systems as proposed in order to design an internal controller with more flexibility and to apply the proposed Virtual Input controller to real processes.