1. Introduction
Hydrodynamic step bearings are one of the important types of thrust bearings to support the axial loads in rotating machines[1]. Classical hydrodynamic lubrication theory[2], which assumes Newtonian fluid, smooth bearing surfaces, and isothermal conditions, was ever often used in the design of these bearings. It may be suitable for light operating conditions but inadequate for relatively heavy loads and relatively high sliding speeds, where the effects of the fluid non-Newtonian shear thinning and the fluid film viscous heating are significant. When the latter two effects were incorporated in studying the performance of the hydrodynamic thrust bearings, the hydrodynamic film thickness in the bearings was significantly reduced[3-8]. Also, in large-size thrust bearings, such as operating in hydro generators with heavy loads and high sliding speeds, the hydrodynamic film thickness was found to be unexpectedly low or even vanishing[9-11]. It was ascribed to the effect of the thermoelastic deformation of the bearing surfaces[9-11].
Admittedly, classical hydrodynamic lubrication theory based on the continuum Reynolds equation may stand for the condition of relatively high film thicknesses where the lubricating media across the whole bearing clearance can be considered a continuum. But it intrinsically fails for the condition of low bearing clearance where the effect of the adsorbed layer on the bearing surface is involved or the local area in the bearing is directly in the boundary lubrication with only the adsorbed molecule layers present (typically on the 1nm scale of the thickness); a thin adsorbed boundary layer is essentially non-continuum with the evolved rheological properties owing to the interaction between the fluid and the bearing surface. Zhang has pointed out these disciplines and made the corresponding analysis for the thrust bearing with parallel surfaces and for the multiscale flow in a small surface clearance[12, 13].
The hydrodynamic lubricating film thicknesses on mechanical components are not always high, so the continuum Reynolds equation is not always valid. In modern industry, with the increases in load and sliding speed, they are frequently low and the lubrication phenomena cannot be explained with classical hydrodynamic lubrication theory. This particularly occurs in the macro hydrodynamic thrust bearing with heavy loads, high sliding speeds, or/and big geometrical sizes[9-11]. On the other hand, the sizes of the mechanical elements are becoming micrometer-scale or even nanometer-scale nowadays, such as those in micromachines[14-16]. The bearings in these mechanical systems are essentially very small, and the lubricating film thicknesses in these bearings are intrinsically very low, such as the 1nm scale. It is thus necessary to develop new calculation methods for the design of these macro or micro thrust bearings with fairly low clearances for which classical calculation methods fail.
In the past study[17], we computed the hydrodynamic pressures in the step bearing with low clearance in which the adsorbed layer effect is described by the multiscale approach proposed by Zhang[13], which considers both the adsorbed layer flow and the intermediate continuum fluid flow. In that study, the bearing surfaces were assumed identical and the corresponding multiscale flow equations were applied[13].
If the bearing clearance is only several nanometers, the interaction between the fluid and the static surface is shown to increase significantly the hydrodynamic pressure of the slider bearing in the boundary lubrication if compared to the classical calculation[12]. For these bearings, as shown, the fluid-static surface interaction in the inlet zone ought to be stronger than in the outlet zone for higher hydrodynamic pressures to be achieved[12]. However, the question of whether such an effect is also present in the hydrodynamic step bearing with low clearance, which is in another mode of lubrication with the continuum fluid film intervening between the two adsorbed layers, is consequently being raised. The present study aims to address this topic. It will be of particular interest to the design of the macro or micro hydrodynamic step bearings with low clearances for improving their load-carrying capacity.
Huang and Zhang[18] presented the corresponding mathematical equations for the two adsorbed layers flow and the intermediate continuum fluid flow in the two-dimensional flow problem in which the coupled surfaces are different. Their flow equations are used to perform the analysis. Different from the classical multiscale approaches[19-22], the present study derives the closed-form explicit formula for calculating the hydrodynamic pressure and the carried load of the bearing.
2. The studied micro hydrodynamic step bearing
As an exemplary case, the present paper studies the performance of the micro hydrodynamic step bearing with the width size (l1+l2) on a scale of 1μm-1mm and with the surface clearance on the scales of 10nm-100nm, as shown in Figure 1. The results and conclusions obtained for this bearing can be extended to the macro-size hydrodynamic step bearing with the width size on the scales of 10mm-100mm and with the surface clearance on the scales of 10nm-100nm, as typically occurring in large power axial supporters. In the present study on the bearing, the effect of the adsorbed layers on both bearing surfaces should be taken into account. There is a continuum fluid film between the two adsorbed layers that results in multiscale flow in the whole bearing. In this bearing, on the upper static surface, the surface property in the inlet zone is different from that in the outlet zone; the lower surface with the speed u has the same property everywhere. The used coordinate is also shown. Table 1 shows the interaction combinations used in this study.
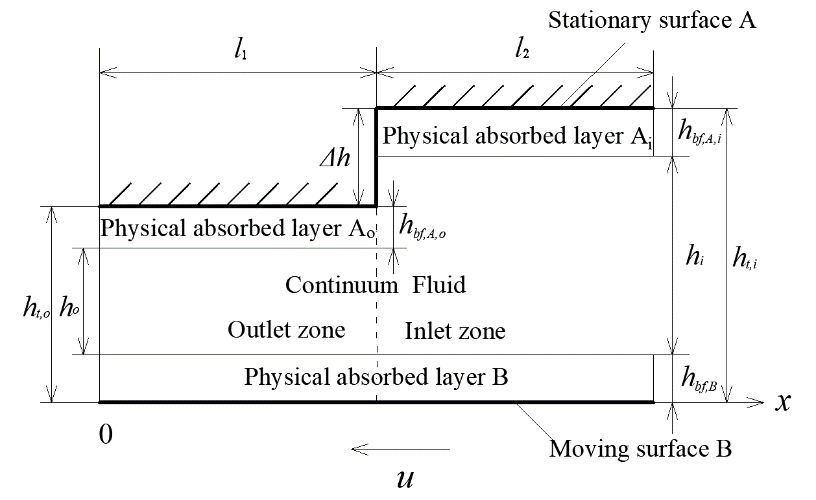
Fig. 1 The studied multiscale hydrodynamic step bearing with small clearance where the upper static surfaces in the inlet and outlet zones are different
Table 1 The interaction combinations between the fluid and the bearing surfaces
|
Symbols
|
Interaction forming adsorbed layer Ao
|
Interaction forming adsorbed layer Ai
|
Interaction forming adsorbed layer B
|
|
S-M-S
|
Strong
|
Medium
|
Strong
|
|
S-W-S
|
Strong
|
Weak
|
Strong
|
|
M-S-S
|
Medium
|
Strong
|
Strong
|
|
W-S-S
|
Weak
|
Strong
|
Strong
|
|
S-S-S
|
Strong
|
Strong
|
Strong
|
3. Mathematical derivations
The two basic flow equations (Eqs. (1) and (10)) used in the present study are adopted from Huang and Zhang[18] for the multiscale flow between two different solid surfaces and the details can be found in their work. Based on these two flow equations, in this paper, the detailed mathematical equations are then newly derived for the present specific bearing. The present study takes the assumptions as the negligible slide leakage, the perfect smooth bearing surfaces, the isothermal and steady-state flow, the negligible fluid compressibility due to pressure, the negligible fluid piezo-viscous effect, the Newtonian fluid, and no wall slippage.
3.1 In the inlet zone
The total mass flow rate per unit contact length through the inlet zone is[18]:
(1)where [TeX:] \lambda_{\text{bf},A,i} = h_{\text{bf},A,i}/h_{i}, [TeX:] q_{0,A,o} = \Delta_{j + 1,A,o}/\Delta_{j,A,o}, u is positive, and the definitions of the other parameters are shown in Ref.[5] and in the nomenclature.
From Eq. (1) is obtained:
[TeX:] p(x) = \frac{M_{1}x + c_{1}}{A_{1}^{\ }\ }
(2)
where c1 is constant and:
[TeX:] \begin{matrix}
A_{1} = \frac{F_{1,A,i}h_{bf,A,i}^{3}\rho_{bf,A,i}^{\text{eff}}}{12\eta_{bf,A,i}^{\text{eff}}} + \frac{F_{1,B}h_{bf,B}^{3}\rho_{bf,B}^{\text{eff}}}{12\eta_{bf,B}^{\text{eff}}} - \frac{\rho{h_{i}}^{3}}{12\eta} + \frac{\varepsilon_{A,i}\lambda_{bf,A,i}\rho_{bf,A,i}^{\text{eff}}}{\lambda_{bf,A,i}\left( \text{II}I_{i} + 1 \right) + Cy_{A,i}\left( 1 + \frac{\text{Δx}}{D} \right)}\left\{ \frac{F_{2,B}h_{bf,B}^{2}h_{bf,A,i}}{12\eta_{bf,B}^{\text{eff}}} - \frac{F_{2,A,i}h_{bf,A,i}^{3}}{12\eta_{bf,A,i}^{\text{eff}}} \right.\ - h_{bf,A,i}^{3} \\
\ \ \ \ \cdot \frac{\text{II}I_{i} + \frac{Cy_{A,i}}{\lambda_{bf,A,i}}\left( 1 + \frac{\text{Δx}}{D} \right)}{2\eta_{bf,A,i}^{\text{eff}}\left( 1 + \frac{\text{Δx}}{D} \right)}\left( 1 + \frac{1}{2\lambda_{bf,A,i}} - \frac{q_{0,A,i} - q_{0,A,i}^{n'}}{q_{0,A,i}^{n' - 1} - q_{0,A,i}^{n'}}\frac{\Delta_{n' - 2}}{h_{bf,A,i}} \right) - \frac{\text{II}I_{i}h_{bf,B}{h_{bf,A}^{2}}_{,i}}{2\eta_{bf,A,i}^{\text{eff}}\left( 1 + \frac{\text{Δx}}{D} \right)}\left. \ \left( 1 + \frac{1}{2\lambda_{bf,B,i}} - \frac{q_{0,B} - q_{0,B}^{m}}{q_{0,B}^{m - 1} - q_{0,B}^{m}}\frac{\Delta_{m - 2}}{h_{bf,B}} \right) \right\} \\
\ \ \ + \frac{\varepsilon_{B}\lambda_{bf,B,i}\rho_{bf,B}^{\text{eff}}}{\lambda_{bf,B,i}\left( 1 + \frac{1}{\text{II}I_{i}} \right) + Cy_{B}\left( 1 + \frac{\text{Δx}}{D} \right)}\left\{ \frac{F_{2,A,i}h_{bf,A,i}^{2}h_{bf,B}}{12\eta_{bf,A,i}^{\text{eff}}} \right.\ - \left\lbrack \frac{1}{\text{II}I_{i}} + \frac{Cy_{B}}{\lambda_{bf,B,i}}\left( 1 + \frac{\text{Δx}}{D} \right) \right\rbrack\left( 1 + \frac{1}{2\lambda_{bf,B,i}} - \frac{q_{0,B} - q_{0,B}^{m}}{q_{0,B}^{m - 1} - q_{0,B}^{m}}\frac{\Delta_{m - 2}}{h_{bf,B}} \right) \\
\ \ \ \ \cdot \frac{h_{bf,B}^{3}}{2\eta_{bf,B}^{\text{eff}}\left( 1 + \frac{\text{Δx}}{D} \right)} - \frac{h_{bf,A,i}h_{bf,B}^{2}}{2III_{i}\eta_{bf,B}^{\text{eff}}\left( 1 + \frac{\text{Δx}}{D} \right)}\left. \ \left( 1 + \frac{1}{2\lambda_{bf,A,i}} - \frac{q_{0,A,i} - q_{0,A,i}^{n'}}{q_{0,A,i}^{n' - 1} - q_{0,A,i}^{n'}}\frac{\Delta_{n' - 2}}{h_{bf,A,i}} \right) - \frac{F_{2,B}h_{bf,B}^{3}}{12\eta_{bf,B}^{\text{eff}}} \right\} - \frac{\rho{h_{i}}^{3}}{2} \\
\ \ \ \ \cdot \left\{ \frac{2III_{i}\lambda_{bf,A,i} + Cy_{A,i}\left( 1 + \frac{\text{Δx}}{D} \right)}{\lambda_{bf,A,i}\left( \text{II}I_{i} + 1 \right) + Cy_{A,i}\left( 1 + \frac{\text{Δx}}{D} \right)} \right.\ \left\lbrack \left( \frac{1}{2} + \lambda_{bf,A,i} - \frac{q_{0,A,i} - q_{0,A,i}^{n'}}{q_{0,A,i}^{n' - 1} - q_{0,A,i}^{n'}}\frac{\Delta_{n' - 2}}{h_{i}} \right) \right.\ \frac{\lambda_{bf,A,i}}{\eta_{bf,A,i}^{\text{eff}}\left( 1 + \frac{\text{Δx}}{D} \right)} + \left. \ \frac{F_{2,A,i}\lambda_{bf,A,i}^{2}}{6\eta_{bf,A,i}^{\text{eff}}} \right\rbrack \\
\ \ \ \ + \frac{2\lambda_{bf,A,i} + Cy_{A,i}\left( 1 + \frac{\text{Δx}}{D} \right)}{\lambda_{bf,A,i}\left( \text{II}I_{i} + 1 \right) + Cy_{A,i}\left( 1 + \frac{\text{Δx}}{D} \right)}\left\lbrack \left( \frac{1}{2} + \lambda_{bf,B,i} - \frac{q_{0,B} - q_{0,B}^{m}}{q_{0,B}^{m - 1} - q_{0,B}^{m}}\frac{\Delta_{m - 2}}{h_{i}} \right) \right.\ \left. \ \frac{\lambda_{bf,B,i}}{\eta_{bf,B}^{\text{eff}}\left( 1 + \frac{\text{Δx}}{D} \right)} + \left. \ \frac{F_{2,B}\lambda_{bf,B,i}^{2}}{6\eta_{bf,B}^{\text{eff}}} \right\rbrack \right\} \\
\end{matrix}
(3)
[TeX:] \begin{matrix}
M_{1} = q_{m} + uh_{\text{bf},B}\rho_{\text{bf},B}^{\text{eff}} + \frac{\text{uh}_{i}^{\ }\ \rho}{2} - \frac{\varepsilon_{B}\lambda_{\text{bf},B,i}uh_{\text{bf},B}\rho_{\text{bf},B}^{\text{eff}}}{2\lambda_{\text{bf},B,i}\left( 1 + \frac{1}{\text{II}I_{i}} \right) + 2Cy_{B}\left( 1 + \frac{\Delta x}{D} \right)} \\
\text{\ \ \ \ \ \ } + \frac{u\lambda_{\text{bf},A,i}\left\lbrack h_{i}\rho\left( 1 - III_{i} \right) + \varepsilon_{A,i}h_{\text{bf},A,i}\rho_{\text{bf},A,i}^{\text{eff}} \right\rbrack}{2\lambda_{\text{bf},A,i}\left( \text{II}I_{i} + 1 \right) + 2Cy_{A,i}\left( 1 + \frac{\Delta x}{D} \right)} \\
\end{matrix}
(4)
According to [TeX:] p|_{x = l_{1} + l_{2}} = 0, from Eq. (2) follows:
[TeX:] c_{1} = - M_{1}\left( l_{1} + l_{2} \right)
(5)
The pressure is then expressed as:
[TeX:] p(x) = F_{1,i}\left( x \right) \cdot q_{m} + F_{2,i}\left( x \right),\ \ \ \ \ \ \ \ for\ \ l_{1} \leq x \leq l_{1} + l_{2}
(6)
where:
[TeX:] F_{1,i}\left( x \right) = \frac{x - \left( l_{1} + l_{2} \right)}{A_{1}}
(7)
[TeX:] F_{2,i}\left( x \right) = \frac{\left( M_{1} - q_{m} \right)\left\lbrack x - \left( l_{1} + l_{2} \right) \right\rbrack}{A_{1}}
(8)
Equation (6) gives the following boundary pressure:
[TeX:] p|_{x = l_{1}} = F_{1,i}\left( l_{1} \right) \cdot q_{m} + F_{2,i}\left( l_{1} \right)
(9)
3.2 In the outlet zone
The total mass flow rate per unit contact length through the outlet zone is[18]:
(10)
where [TeX:] \lambda_{\text{bf},A,o} = h_{\text{bf},A,o}/h_{o}, [TeX:] \lambda_{\text{bf},B,o} = h_{\text{bf},B}/h_{o}, and the definitions of the other parameters are shown in Ref.[5] and in the nomenclature.
From Eq. (10) is derived:
[TeX:] p(x) = \frac{M_{2}x + c_{2}}{A_{2}}
(11)
where c2 is constant and:
[TeX:] \begin{matrix}
A_{2} = \frac{F_{1,A,o}h_{\text{bf},A,o}^{3}\rho_{\text{bf},A,o}^{\text{eff}}}{12\eta_{\text{bf},A,o}^{\text{eff}}} + \frac{F_{1,B}h_{\text{bf},B}^{3}\rho_{\text{bf},B}^{\text{eff}}}{12\eta_{\text{bf},B}^{\text{eff}}} - \frac{\rho{h_{o}}^{3}}{12\eta} + \frac{\varepsilon_{A,o}\lambda_{\text{bf},A,o}\rho_{\text{bf},A,o}^{\text{eff}}}{\lambda_{\text{bf},A,o}\left( \text{II}I_{o} + 1 \right) + Cy_{A,o}\left( 1 + \frac{\Delta x}{D} \right)}\left\{ \frac{F_{2,B}h_{\text{bf},B}^{2}h_{\text{bf},A,o}}{12\eta_{\text{bf},B}^{\text{eff}}} - \frac{F_{2,A,o}h_{\text{bf},A,o}^{3}}{12\eta_{\text{bf},A,o}^{\text{eff}}} \right.\ - h_{\text{bf},A,o}^{3} \\
\text{\ \ \ \ \ } \cdot \frac{\text{II}I_{o} + \frac{Cy_{A,o}}{\lambda_{\text{bf},A,o}}\left( 1 + \frac{\Delta x}{D} \right)}{2\eta_{\text{bf},A,i}^{\text{eff}}\left( 1 + \frac{\Delta x}{D} \right)}\left( 1 + \frac{1}{2\lambda_{\text{bf},A,o}} - \frac{q_{0,A,o} - q_{0,A,o}^{n'}}{q_{0,A,o}^{n' - 1} - q_{0,A,o}^{n'}}\frac{\Delta_{n' - 2}}{h_{\text{bf},A,o}} \right) - \frac{\text{II}I_{o}h_{\text{bf},B}{h_{\text{bf},A}^{2}}_{,o}}{2\eta_{\text{bf},A,o}^{\text{eff}}\left( 1 + \frac{\Delta x}{D} \right)}\left. \ \left( 1 + \frac{1}{2\lambda_{\text{bf},B,o}} - \frac{q_{0,B} - q_{0,B}^{m}}{q_{0,B}^{m - 1} - q_{0,B}^{m}}\frac{\Delta_{m - 2}}{h_{\text{bf},B}} \right) \right\} \\
\text{\ \ \ \ } + \frac{\varepsilon_{B}\lambda_{\text{bf},B,o}\rho_{\text{bf},B}^{\text{eff}}}{\lambda_{\text{bf},B,o}\left( 1 + \frac{1}{\text{II}I_{o}} \right) + Cy_{B}\left( 1 + \frac{\Delta x}{D} \right)}\left\{ \frac{F_{2,A,o}h_{\text{bf},A,o}^{2}h_{\text{bf},B}}{12\eta_{\text{bf},A,o}^{\text{eff}}} \right.\ - \left\lbrack \frac{1}{\text{II}I_{o}} + \frac{Cy_{B}}{\lambda_{\text{bf},B,o}}\left( 1 + \frac{\Delta x}{D} \right) \right\rbrack\left( 1 + \frac{1}{2\lambda_{\text{bf},B,o}} - \frac{q_{0,B} - q_{0,B}^{m}}{q_{0,B}^{m - 1} - q_{0,B}^{m}}\frac{\Delta_{m - 2}}{h_{\text{bf},B}} \right) \\
\text{\ \ \ \ \ } \cdot \frac{h_{\text{bf},B}^{3}}{2\eta_{\text{bf},B}^{\text{eff}}\left( 1 + \frac{\Delta x}{D} \right)} - \frac{h_{\text{bf},A,o}h_{\text{bf},B}^{2}}{2\text{II}I_{o}\eta_{\text{bf},B}^{\text{eff}}\left( 1 + \frac{\Delta x}{D} \right)}\left. \ \left( 1 + \frac{1}{2\lambda_{\text{bf},A,o}} - \frac{q_{0,A,o} - q_{0,A,o}^{n'}}{q_{0,A,o}^{n' - 1} - q_{0,A,o}^{n'}}\frac{\Delta_{n' - 2}}{h_{\text{bf},A,o}} \right) - \frac{F_{2,B}h_{\text{bf},B}^{3}}{12\eta_{\text{bf},B}^{\text{eff}}} \right\} - \frac{\rho{h_{o}}^{3}}{2} \\
\text{\ \ \ } \cdot \left\{ \frac{2\text{II}I_{o}\lambda_{\text{bf},A,o} + Cy_{A,o}\left( 1 + \frac{\Delta x}{D} \right)}{\lambda_{\text{bf},A,o}\left( \text{II}I_{o} + 1 \right) + Cy_{A,o}\left( 1 + \frac{\Delta x}{D} \right)} \right.\ \left\lbrack \left( \frac{1}{2} + \lambda_{\text{bf},A,o} - \frac{q_{0,A,o} - q_{0,A,o}^{n'}}{q_{0,A,o}^{n' - 1} - q_{0,A,o}^{n'}}\frac{\Delta_{n' - 2}}{h_{o}} \right) \right.\ \frac{\lambda_{\text{bf},A,o}}{\eta_{\text{bf},A,o}^{\text{eff}}\left( 1 + \frac{\Delta x}{D} \right)} + \left. \ \frac{F_{2,A,o}\lambda_{\text{bf},A,o}^{2}}{6\eta_{\text{bf},A,o}^{\text{eff}}} \right\rbrack \\
\text{\ \ \ } + \frac{2\lambda_{\text{bf},A,o} + Cy_{A,o}\left( 1 + \frac{\Delta x}{D} \right)}{\lambda_{\text{bf},A,o}\left( \text{II}I_{o} + 1 \right) + Cy_{A,o}\left( 1 + \frac{\Delta x}{D} \right)}\left\lbrack \left( \frac{1}{2} + \lambda_{\text{bf},B,o} - \frac{q_{0,B} - q_{0,B}^{m}}{q_{0,B}^{m - 1} - q_{0,B}^{m}}\frac{\Delta_{m - 2}}{h_{o}} \right) \right.\ \left. \ \frac{\lambda_{\text{bf},B,o}}{\eta_{\text{bf},B}^{\text{eff}}\left( 1 + \frac{\Delta x}{D} \right)} + \left. \ \frac{F_{2,B}\lambda_{\text{bf},B,o}^{2}}{6\eta_{\text{bf},B}^{\text{eff}}} \right\rbrack \right\} \\
\end{matrix}
(12)
[TeX:] \begin{matrix}
M_{2} = q_{m} + uh_{\text{bf},B}\rho_{\text{bf},B}^{\text{eff}} + \frac{\text{uh}_{o}^{\ }\ \rho}{2} - \frac{\varepsilon_{B}\lambda_{\text{bf},B,o}uh_{\text{bf},B}\rho_{\text{bf},B}^{\text{eff}}}{2\lambda_{\text{bf},B,o}\left( 1 + \frac{1}{\text{II}I_{o}} \right) + 2Cy_{B}\left( 1 + \frac{\Delta x}{D} \right)} \\
\text{\ \ \ \ \ \ } + \frac{u\lambda_{\text{bf},A,o}\left\lbrack h_{o}\rho\left( 1 - III_{o} \right) + \varepsilon_{A,o}h_{\text{bf},A,o}\rho_{\text{bf},A,o}^{\text{eff}} \right\rbrack}{2\lambda_{\text{bf},A,o}\left( \text{II}I_{o} + 1 \right) + 2Cy_{A,o}\left( 1 + \frac{\Delta x}{D} \right)} \\
\end{matrix}
(13)
According to [TeX:] p|_{x = 0} = 0, from Eq.(11) is obtained that c2=0. The pressure in the outlet zone is then expressed as:
[TeX:] p(x) = F_{1,o}\left( x \right) \cdot q_{m} + F_{2,o}\left( x \right),\ \ \ \ \ \ \ \ \ \ \ for\ 0 \leq x \leq l_{1}
(14)
where:
[TeX:] F_{1,o}\left( x \right) = \frac{x}{A_{2}}
(15)
[TeX:] F_{2,o}\left( x \right) = \frac{\left( M_{2} - q_{m} \right)x}{A_{2}}
(16)
Equation (13) gives the boundary pressure as:
[TeX:] p|_{x = l_{1}} = F_{1,o}\left( l_{1} \right) \cdot q_{m} + F_{2,o}\left( l_{1} \right)
(17)
3.3 Mass flow rate and carried load of the bearing
According to the coupled equations (8) and (15), qm is solved as:
[TeX:] q_{m} = \frac{F_{2,o}\left( l_{1} \right) - F_{2,i}\left( l_{1} \right)}{F_{1,i}\left( l_{1} \right) - F_{1,o}\left( l_{1} \right)}
(18)
The load of the bearing is then:
[TeX:] w = \int_{0}^{l_{1} + l_{2}}\text{pdx} = \frac{\left( q_{m} + M_{2} \right){l_{1}}^{2}}{2A_{2}} - \frac{\left( q_{m} + M_{1} \right){l_{2}}^{2}}{2A_{1}}
(19)
4. Exemplary calculation
The calculations are performed for the following input parameter values:
[TeX:] \Delta_{n' - 2}/D = \Delta_{n'' - 2}/D = \Delta_{m - 2}/D = \Delta x/D = 0.15, [TeX:] D = 0.5nm, [TeX:] l_{1} + l_{2} = 20\mu m
The parameters [TeX:] Cq_{A,i}, [TeX:] Cq_{A,o} and [TeX:] Cq_{B} are generally expressed as[23]:
[TeX:] \text{Cq}(H_{\text{bf}}) = \left\{ \begin{matrix}
1 \\
m_{0} + m_{1}H_{\text{bf}} + m_{2}{H_{\text{bf}}}^{2} + m_{3}{H_{\text{bf}}}^{3} \\
\end{matrix}\begin{matrix}
\\
\\
\end{matrix}\text{\ \ \ \ \ \ \ \ \ }\begin{matrix}
\text{for\ }H_{\text{bf}} \geq 1 \\
for\ 0 < H_{\text{bf}} \leq 1 \\
\end{matrix} \right.\
(20)
where [TeX:] H_{\text{bf}} is [TeX:] H_{\text{bf},A,i},[TeX:] H_{\text{bf},A,o}or [TeX:] H_{\text{bf},B}, [TeX:] H_{\text{bf},A,i} = h_{\text{bf},A,i}/h_{\text{cr},\text{bf},A,i},[TeX:] H_{\text{bf},A,o} = h_{\text{bf},A,o}/h_{\text{cr},\text{bf},A,o}, [TeX:] H_{\text{bf},B} = h_{\text{bf},B}/h_{\text{cr},\text{bf},B}, [TeX:] h_{\text{cr},\text{bf},A,i}and [TeX:] h_{\text{cr},\text{bf},A,o}: being respectively the critical thicknesses for characterizing the rheological properties of the adsorbed layers on the static surface in the inlet and outlet zones, [TeX:] h_{\text{cr},\text{bf},B}; the critical thickness for characterizing the rheological properties of the adsorbed layer on the moving surface, m0, m1, m2 and m3; and constants dependent on the fluid-bearing surface interaction.
The parameters [TeX:] Cy_{A,i}, [TeX:] Cy_{A,o} and [TeX:] Cy_{B} are generally expressed as [23]:
[TeX:] \text{Cy}(H_{\text{bf}}) = \left\{ \begin{matrix}
1 \\
a_{0} + \frac{a_{1}}{H_{\text{bf}}} + \frac{a_{2}}{{H_{\text{bf}}}^{2}} \\
\end{matrix}\ \begin{matrix}
\\
\\
\end{matrix}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ }\begin{matrix}
\text{for\ }H_{\text{bf}} \geq 1 \\
for\ 0 < H_{\text{bf}} \leq 1 \\
\end{matrix} \right.\
(21)
where [TeX:] H_{\text{bf}} is [TeX:] H_{\text{bf},A,i},[TeX:] H_{\text{bf},A,o}or [TeX:] H_{\text{bf},B}, and a0, a1 and a2 are constant, respectively.
The parameters F1, F2 and ε are respectively formulated as[13]:
[TeX:] F_{1} = 0.18\left( \frac{\Delta_{n - 2}}{D} - 1.905 \right)\left( \ln n - 7.897 \right)
(22)
[TeX:] F_{2} = ( - 3.707E - 4)\left( \frac{\Delta_{n - 2}}{D} - 1.99 \right)\left( n + 64 \right)\left( q_{0} + 0.19 \right)\left( \gamma + 42.43 \right)
(23)
[TeX:] \varepsilon = (4.56E - 6)\left( \frac{\Delta_{n - 2}}{D} + 31.419 \right)\left( n + 133.8 \right)\left( q_{0} + 0.188 \right)\left( \gamma + 41.62 \right)
(24)
where [TeX:] F_{1} is [TeX:] F_{1,A,i}, [TeX:] F_{1,A,o}or [TeX:] F_{1,B}, [TeX:] F_{2} is [TeX:] F_{2,A,i}, [TeX:] F_{2,A,o}or [TeX:] F_{2,B}, [TeX:] \varepsilon is [TeX:] \varepsilon_{A,i},[TeX:] \varepsilon_{A,o}or [TeX:] \varepsilon_{B}, [TeX:] n is [TeX:] n', [TeX:] n'' or [TeX:] m, [TeX:] \Delta_{n - 2} is [TeX:] \Delta_{n' - 2}, [TeX:] \Delta_{n'' - 2} or [TeX:] \Delta_{m - 2}, [TeX:] \gamma is [TeX:] \gamma_{A,i}, [TeX:] \gamma_{A,o} or [TeX:] \gamma_{B}.
hbf is calculated as:
[TeX:] h_{\text{bf}} = nD + \frac{q_{0} - q_{0}^{n}}{q_{0}^{n - 1} - q_{0}^{n}}\Delta_{n - 2}
(25)
where hbf is [TeX:] h_{\text{bf},A,i}, [TeX:] h_{\text{bf},A,o} or [TeX:] h_{\text{bf},B}, [TeX:] n is [TeX:] n', [TeX:] n'' or [TeX:] m, [TeX:] q_{0} is [TeX:] q_{0,A,i}, [TeX:] q_{0,A,o} or [TeX:] q_{0,B}.
The weak, medium, and strong interactions between the fluid and the bearing surface were considered. The corresponding parameter values are as follows:
Weak interaction: [TeX:] h_{\text{cr},\text{bf}}=7nm, y=0.5, n=3, q0=1.05
Medium interaction: [TeX:] h_{\text{cr},\text{bf}}=20nm, y=1.0, n=5, q0=1.1
Strong interaction: [TeX:] h_{\text{cr},\text{bf}}=40nm, y=1.5, n=8, q0=1.2
Here, [TeX:] h_{\text{cr},\text{bf}} is [TeX:] h_{\text{cr},\text{bf},A,i}, [TeX:] h_{\text{cr},\text{bf},A,o} or [TeX:] h_{\text{cr},\text{bf},B}, [TeX:] \gamma is [TeX:] \gamma_{A,i}, [TeX:] \gamma_{A,o} or [TeX:] \gamma_{B}, [TeX:] n is [TeX:] n', [TeX:] n'' or [TeX:] m, q0 is [TeX:] q_{0,A,i}, [TeX:] q_{0,A,o} or [TeX:] q_{0,B}. The viscosity and density parameter values for different interactions have been shown in Refs.[10] and[11], and are not repeated here.
5. Results
All the derived equations above for calculating the hydrodynamic pressure and carried load of the bearing are analytically closed-form and explicit. In the present calculations, thus, no numerical approach is required and the results can be directly calculated using the derived formulas based on the input operational parameter values. The results obtained from calculation are discussed in detail, as follows.
5.1 Pressure distribution
For ht,0=20nm and ψ=1, Figures 2(a) to 2(c) show the dimensionless film pressures in the bearing for different interaction combinations. In Figure 2(a), when the step size ∆h is 1nm, the designed inhomogeneous static surfaces are better than the homogeneous static surface due to the higher pressures generated. It is shown that the interaction between the fluid and the static surface in the outlet zone ought to be stronger than that in the inlet zone. This is contrary to the principle of the design of the inhomogeneous static surface in the micro/nano slider bearing in the boundary lubrication[17]. The reason is the modification of the entrainment speed of the continuum film in this bearing caused by the inhomogeneous static surfaces. It is noticed that the larger the difference in the designed inhomogeneous surface properties, the higher the generated hydrodynamic pressures. We also found that for the M-S-S and W-S-S interaction combinations, the pressures cannot be generated in the bearing for the case in Figure 2(a).
Figure 2(b) shows that when ∆h=7nm, the pressures for the S-M-S interaction combination are overlaid with those for the S-S-S interaction combination; while for the S-W-S interaction combination, the pressures are a bit lower; for the M-S-S and W-S-S interaction combinations, the pressures are even lower. Figure 2(b) shows that for the step size, which is big enough, an inhomogeneous static surface is not beneficial to the bearing performance. Figure 2(c) indicates this point, when ∆h=12nm, more clearly. In Figure 2(c), the pressures generated for the S-S-S interaction combination are significantly higher than those for inhomogeneous static surfaces.
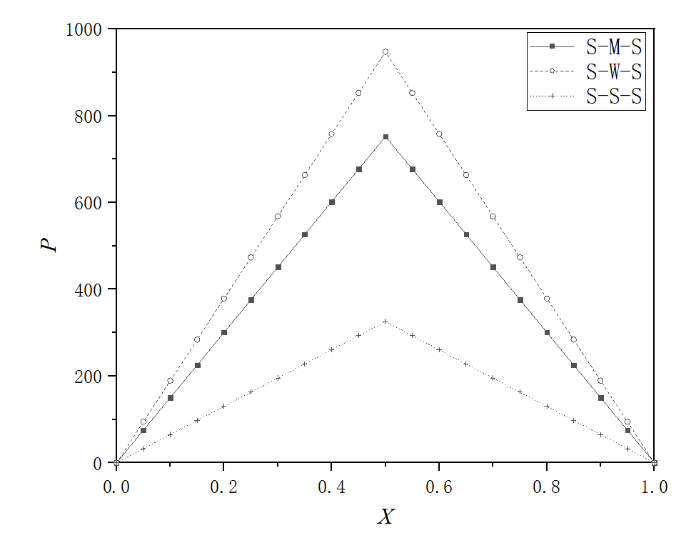
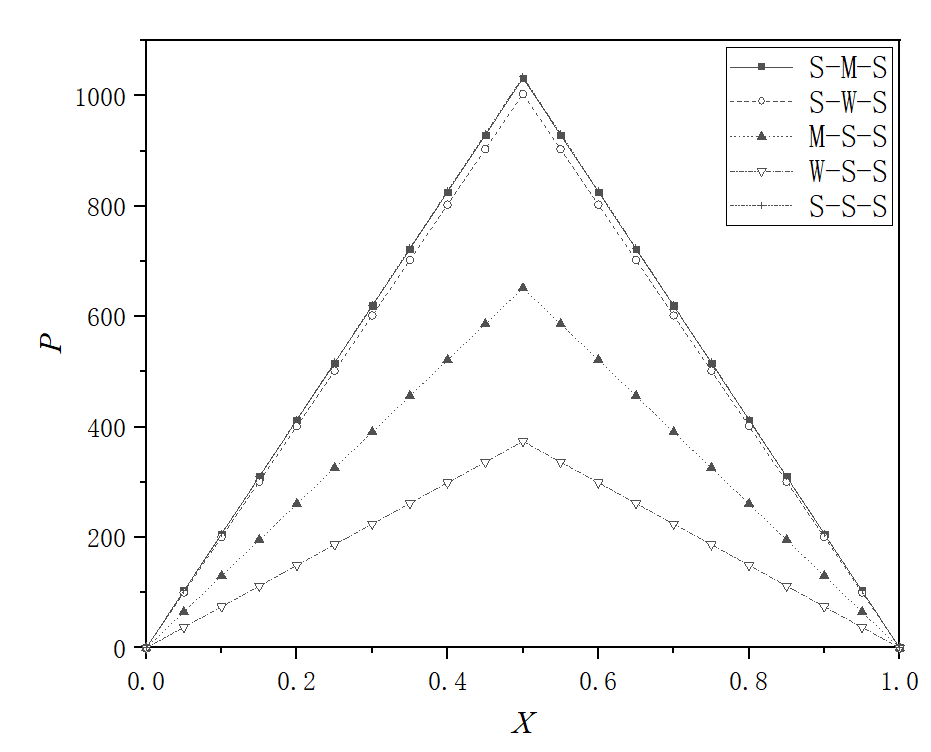
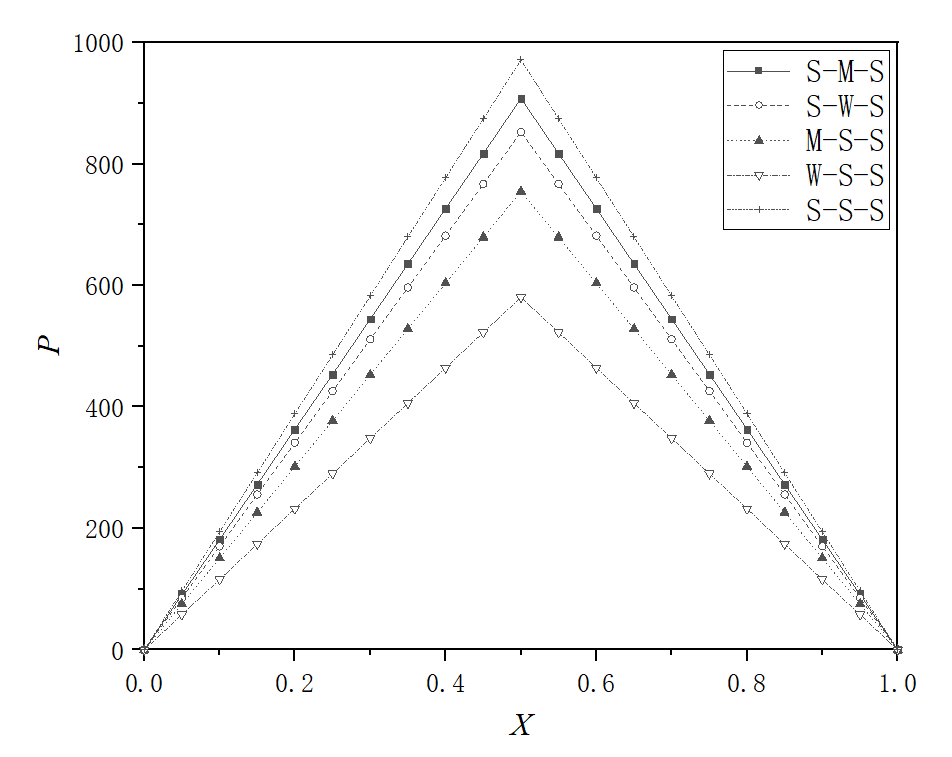
Fig. 2 Bearing pressure distributions for different interaction combinations when ht,0=20nm, and ψ=1
5.2 Bearing load
Figure 3 shows the calculated dimensionless loads carried by the present bearing for different interaction combinations when ψ=1 and ∆h=1nm. The load-carrying capacity of the bearing in the sequence is the S-W-S, S-M-S, and S-S-S interaction combinations. The designed inhomogeneous static surface is obviously advantageous over the homogeneous static surface.
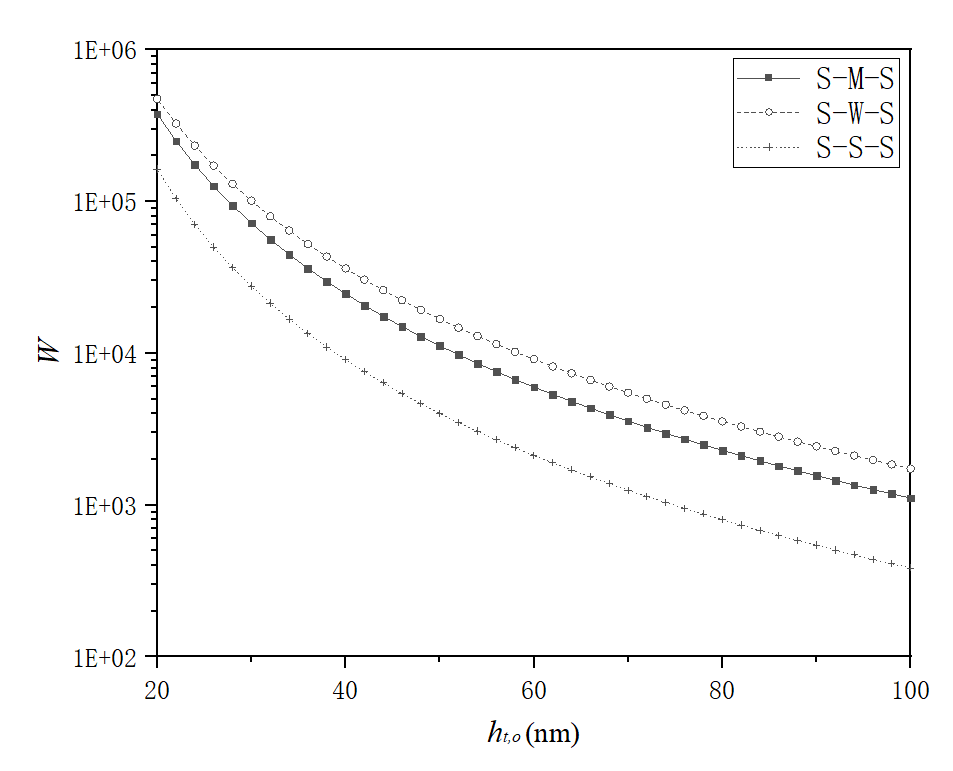
Fig. 3 Dimensionless loads of the bearinght,o for different interaction combinations when ψ=1 and ∆h=1nm
Figure 4(a) shows that when ht,0=20nm and ψ=1, for the step size ∆h less than 7nm the inhomogeneous static surface with the S-W-S or S-M-S interaction combinations is advantageous over the homogeneous static surface owing to the larger load of the bearing; for ∆h>7nm the homogeneous static surface is the most advantageous because of the largest load of the bearing.
In Figure 4 (b), for ht,0=20nm and ∆h=1nm, there are optimum values of ψ which are around 0.6 for the maximum load of the bearing, respectively for the S-W-S and S-M-S interaction combinations. The behaviour for the S-S-S interaction combinations is obviously different.
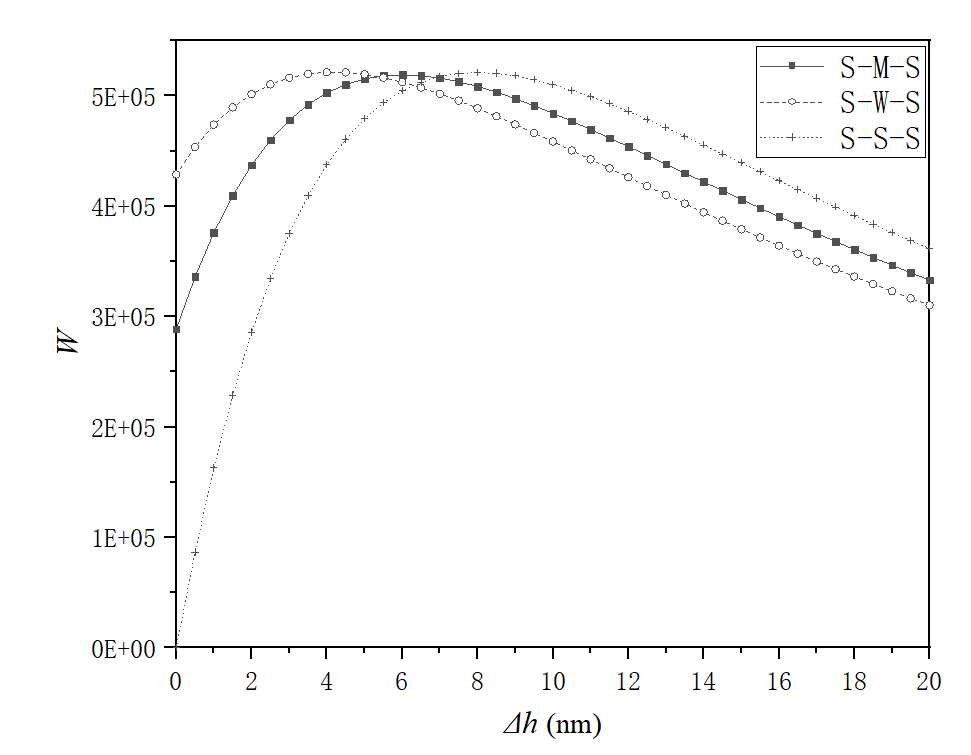
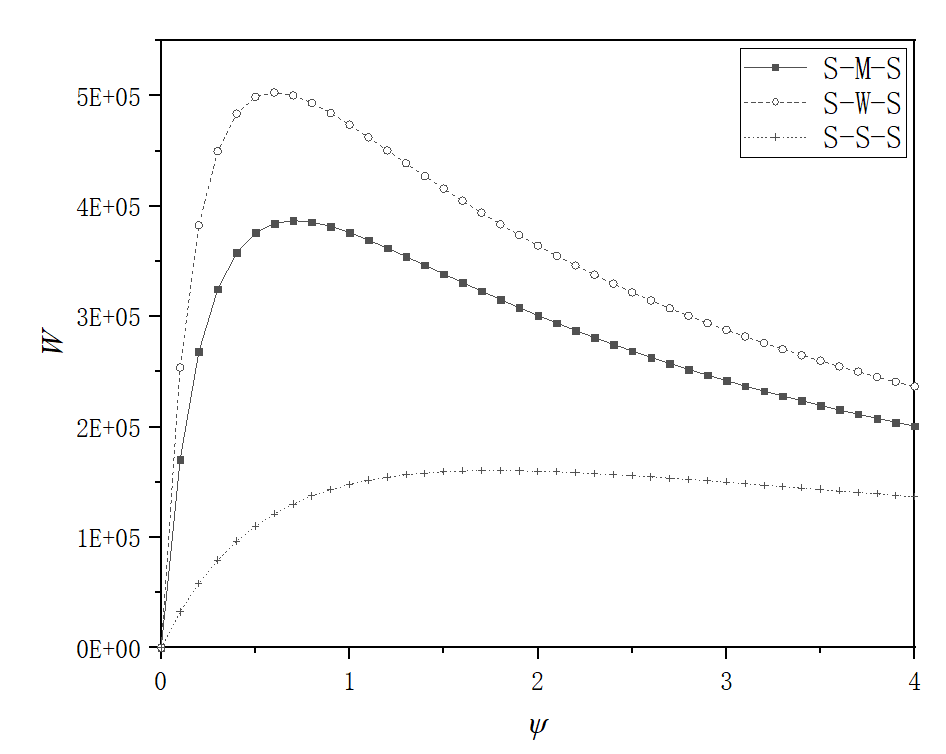
Fig. 4 Dimensionless loads of the bearing against ψ and ∆h for different interaction combinations when ht,0=20nm
6. Conclusions
The multiscale calculation has been performed for the hydrodynamic pressure and load of the micro hydrodynamic step bearing when the static surfaces in the inlet and outlet zones are different. The study considers the effect of the adsorbed layer on the bearing surface with the Newtonian fluid film between the two adsorbed layers.
It is shown that whether the inhomogeneous static surface is advantageous over the homogeneous static surface depends on the bearing step size ∆h. When ∆h is small enough (e.g., less than 7nm), the inhomogeneous static surface should be significantly advantageous over the homogeneous static surface owing to the greater load-carrying capacity of the bearing and the interaction between the fluid and the static surface in the outlet zone ought to be stronger than that in the inlet zone. When ∆h is over large (e.g., more than 7nm), the homogeneous static surface is the most advantageous owing to the greatest load-carrying capacity of the bearing. The present study is significant for the design of the micro hydrodynamic step bearing occurring in micromechanical systems. It is also of significant implication in designing the macro-size hydrodynamic step bearing operating in severe conditions with very low clearances, such as hydro generators, Therefore, the results obtained can be applied to those bearings.
Nomenclature:
a0, a1, a2 constants
[TeX:] Cq_{A,i}
[TeX:] \rho_{\text{bf},A,i}^{\text{eff}}/\rho
[TeX:] Cq_{A,o}
[TeX:] \rho_{\text{bf},A,o}^{\text{eff}}/\rho
[TeX:] Cq_{B}
[TeX:] \rho_{\text{bf},B}^{\text{eff}}/\rho
[TeX:] Cy_{A,i}
[TeX:] \eta_{\text{bf},A,i}^{\text{eff}}/\eta
[TeX:] Cy_{A,o}
[TeX:] \eta_{\text{bf},A,o}^{\text{eff}}/\eta
[TeX:] Cy_{B}
[TeX:] \eta_{\text{bf},B}^{\text{eff}}/\eta
D fluid molecule diameter
h continuum film thickness
[TeX:] h_{\text{bf},A,i} adsorbed layer thickness on the static surface in the inlet zone
[TeX:] h_{\text{bf},A,o} adsorbed layer thickness on the static surface in the outlet zone
[TeX:] h_{\text{bf},B} adsorbed layer thickness on the moving surface
[TeX:] h_{\text{cr},\text{bf},A,i} critical thickness for characterizing the rheological properties of the adsorbed layer on the static surface in the inlet zone
[TeX:] h_{\text{cr},\text{bf},A,o} critical thickness for characterizing the rheological properties of the adsorbed layer on the static surface in the outlet zone
[TeX:] h_{\text{cr},\text{bf},B} critical thickness for characterizing the rheological properties of the adsorbed layer on the moving surface
hi, h0 continuum film thicknesses on the bearing entrance and exit, respectively
ht,0 surface separation on the bearing exit
[TeX:] H_{\text{bf},A,i}
[TeX:] h_{\text{bf},A,i}/h_{\text{cr},\text{bf},A,i}
[TeX:] H_{\text{bf},B,o}
[TeX:] h_{\text{bf},A,o}/h_{\text{cr},\text{bf},A,o}
[TeX:] H_{\text{bf},B}
[TeX:] h_{\text{bf},B}/h_{\text{cr},\text{bf},B}
i, j order numbers of the fluid molecule across the adsorbed layer thickness respectively
l1, l2 widths of the outlet and inlet zones, respectively
[TeX:] m,[TeX:] n',[TeX:] n'' equivalent numbers of the fluid molecules across the lower adsorbed layer thickness and the upper adsorbed layer thicknesses in the inlet and outlet zones, respectively
m0, m1, m2, m3 constants
n
equivalent number of fluid molecules across the upper adsorbed layer thickness
p hydrodynamic pressure
P dimensionless hydrodynamic pressure
[TeX:] q_{0,A,i},[TeX:] q_{0,A,o},[TeX:] q_{0,B} constants
qm total mass flow rate per unit contact length through the bearing
Qm dimensionless mass flow rate per unit contact length through the bearing, [TeX:] q_{m}/uh_{o}\rho_{a}
u sliding speed
w load per unit contact length of the bearing
W dimensionless load, w/uη
x coordinate
X
[TeX:] x/(l_{1} + l_{2})
ρ fluid bulk density
[TeX:] \rho_{\text{bf},A,i}^{\text{eff}} average density of the upper adsorbed layer in the inlet zone
[TeX:] \rho_{\text{bf},A,o}^{\text{eff}} average density of the upper adsorbed layer in the outlet zone
[TeX:] \rho_{\text{bf},B}^{\text{eff}} average density of the lower adsorbed layer
η fluid bulk viscosity
[TeX:] \eta_{\text{bf},A,i}^{\text{eff}} effective viscosity of the upper adsorbed layer in the inlet zone
[TeX:] \eta_{\text{bf},A,o}^{\text{eff}} effective viscosity of the upper adsorbed layer in the outlet zone
[TeX:] \eta_{\text{bf},B}^{\text{eff}} effective viscosity of the lower adsorbed layer
[TeX:] \eta_{\text{line},j - 1} local viscosity between the jth and (j-1)th fluid molecules across the adsorbed layer thickness
[TeX:] \lambda_{\text{bf},A,i}
[TeX:] h_{\text{bf},A,i}/h_{i}
[TeX:] \lambda_{\text{bf},A,o}
[TeX:] h_{\text{bf},A,o}/h_{o}
[TeX:] \lambda_{\text{bf},B,i}
[TeX:] h_{\text{bf},B}/h_{i}
[TeX:] \lambda_{\text{bf},B,o}
[TeX:] h_{\text{bf},B}/h_{o}
ψ
[TeX:] l_{l}/l_{2}
∆h step size of the bearing
[TeX:] \Delta_{j,A,i}, [TeX:] \Delta_{j,A,o}, [TeX:] \Delta_{j,B} separation between the (j+1)th and jth fluid molecules across the adsorbed layer thickness respectively on the upper bearing surfaces in the inlet and outlet zones and on the lower bearing surface
∆x separation between the neighbouring fluid molecules in the flow direction in the adsorbed layer
[TeX:] \Delta_{n' - 2}, [TeX:] \Delta_{n'' - 2}, [TeX:] \Delta_{m - 2} separations between the neighbouring fluid molecules across the adsorbed layer thicknesses just on the boundaries between the upper adsorbed layer and the continuum fluid in the inlet and outlet zones and between the lower adsorbed layer and the continuum fluid respectively
Subscript:
A on the upper adsorbed layer
B on the lower adsorbed layer
I in the inlet zone
O in the outlet zone







